Прямолинейное движение точки задано уравнение s = 2t ^ 2 — 8t — 10?

Математика | 5 — 9 классы

Прямолинейное движение точки задано уравнение s = 2t ^ 2 — 8t — 10.

Найдите скорость движения точки в конце 8 — й секунды.

При равноускоренном движении пройденное расстояние меняется по формуле :

s = a * t ^ 2 / 2 + v0 * t + s0,

где а — ускорение, v0 — начальная скорость, s0 — начальное расстояние, t — время.

При равноускоренном движении скорость линейно меняется со временем

В данном случае при а = 4, v0 = — 8, t = 8

v(8) = — 8 + 4 * 8 = 24.

Помогите решить : материальная точка движения прямолинейного по закону х(t) = 6t ^ 2 — 48t + 17 где х — расстояние от точки отчета в метрах, t — время в секундах, измеренное с начала движения?

Помогите решить : материальная точка движения прямолинейного по закону х(t) = 6t ^ 2 — 48t + 17 где х — расстояние от точки отчета в метрах, t — время в секундах, измеренное с начала движения.

Найдите ее скорость (в метрах в секунду) в момент времени t = 9c.

Ускорение точки, движущейся прямолинейно, заданно уравнением a = 12t — 2?

Ускорение точки, движущейся прямолинейно, заданно уравнением a = 12t — 2.

Найти закон движения этой точки, если в момент времени t = 2 с её скорость 9 = 5м / с и путь s = 12м.

Ускорение прямолинейного движения точки выражается формулой а = 2t + 3?

Ускорение прямолинейного движения точки выражается формулой а = 2t + 3.

Найти уравнение движения точки, если Vо = 0, S = 0, t = 0.

Скорость точки, движущейся прямолинейно, задана уравнением v(t) = t ^ 2 — 4t + 3(m / с)?

Скорость точки, движущейся прямолинейно, задана уравнением v(t) = t ^ 2 — 4t + 3(m / с).

Какое ускорение будет иметь тело через 5с начала движения?

Скорость движения точки v = 5t + 4t²(м / с)?

Скорость движения точки v = 5t + 4t²(м / с).

Найдите путь пройденный точкой за 3 секунды от начала движения.

Скорость движения точки v = 3t ^ 2 + 4t м / с?

Скорость движения точки v = 3t ^ 2 + 4t м / с.

Найдите путь, пройденный точкой за 3 — ю секунду.

Найдите скорость движения точки, заданной уравнением s = √t , в момент времени t = 1?

Найдите скорость движения точки, заданной уравнением s = √t , в момент времени t = 1.

Скорость точки движущейся прямолинейно, задана уравнением V = (6t ^ 2 — 4t — 10)м / с?

Скорость точки движущейся прямолинейно, задана уравнением V = (6t ^ 2 — 4t — 10)м / с.

Вычислить её путь за 4 секунды от начала движения.

Зависимость пути от времени при прямолинейном движении точки задана уравнением s = t³ — 6t² — 12t + 3?

Зависимость пути от времени при прямолинейном движении точки задана уравнением s = t³ — 6t² — 12t + 3.

В какой момент времени ускорение движения точки будет равно 24м / с²?

Скорость движения точки U = (24t + 6t²) мс найдите путь, пройденный точкой за 5 — 10 секунду?

Скорость движения точки U = (24t + 6t²) мс найдите путь, пройденный точкой за 5 — 10 секунду.

Если вам необходимо получить ответ на вопрос Прямолинейное движение точки задано уравнение s = 2t ^ 2 — 8t — 10?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Математика вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

Прямолинейное движение точки задано уравнением x=-2+3t-0,5t^2 (м). Найти

Условие задачи:

Прямолинейное движение точки задано уравнением \(x=-2+3t-0,5t^2\) (м). Найти путь за 8 с.

Задача №1.3.48 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Решение задачи:

В условии дано уравнение движения точки, давайте попробуем найти как меняется со временем её скорость. Это можно сделать двумя способами.

Первый способ – простой, его следует использовать, если вы не умеете брать производные от функций. В общем случае уравнение прямолинейного ускоренного движения точки выглядит так:

Мы же имеем такое уравнение:

Просто сопоставим эти уравнения. Тогда начальная координата \(x_0\), начальная скорость \(\upsilon _0\) и ускорение \(a\) в нашем случае равны:

Уравнение скорости в общем виде такое:

Подставив полученные нами значения, мы имеем такое уравнение скорости:

Суть второго способа заключается в том, что первая производная от функции координаты есть функция скорости.

\[\upsilon = ( – 2 + 3t – 0,5)’\]

Как видите, мы получили то же самое.

Зная тот факт, что площадь фигуры под графиком зависимости скорости от времени есть пройденный путь, построим график \(\upsilon = 3 – t\) (рисунок справа). Получается, чтобы узнать путь \(S\) нужно посчитать площади двух треугольников и сложить их.

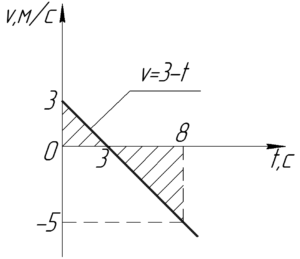
Кстати, расположение этих треугольников (над или под осью) также несет смысл. Если график скорости пересекает ось, значит тело меняет направление своего движения. Поэтому, в случае если мы ищем путь, по полученные площади необходимо сложить, если же мы пытаемся найти перемещение, то нужно отнять из большего меньшее.

Площадь прямоугольных треугольников определяется как половина произведения двух катетов, поэтому ответ такой:

\[S = \frac<1> <2>\cdot 3 \cdot 3 + \frac<1> <2>\cdot \left( <8 – 3>\right) \cdot 5 = 17\; м\]

Наша точка прошла 4,5 м по оси \(x\) и 12,5 м против нее.

Ответ: 17 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Теоретическая механика:
Кинематика точки

Смотрите также решения задач по теме «Кинематика точки» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.

В этой главе в основном рассмотрены методы решения задач, в которых закон движения точки выражен так называемым естественным способом: уравнением s=f(t) по заданной траектории *.

* Решения задач, в которых закон движения задан координатным способом, рассмотрены в конце главы (§ 31).

В этом случае главными параметрами, характеризующими движение точки но заданной траектории, являются: s – расстояние от заданного начального положения и t – время.

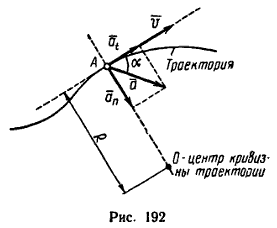
Величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется скоростью (v на рис. 192). Вектор скорости всегда направлен вдоль касательной в ту сторону, куда движется точка. Числовое значение скорости в любой момент времени выражается производной от расстояния по времени:
v = ds/dt или v = f'(t).

Ускорение a точки в каждый данный момент времени характеризует быстроту изменения скорости. При этом нужно отчетливо понимать, что скорость – вектор, и, следовательно, изменение скорости может происходить по двум признакам: по числовой величине (по модулю) и по направлению.

Быстрота изменения модуля скорости характеризуется касательным (тангенсальным) ускорением a_t – составляющей полного ускорения a, направленной по касательной к траектории (см. рис. 192).

Числовое значение касательного ускорения в общем случае определяется по формуле
a_t = dv/dt или a_t = f»(t).

Быстрота изменения направления скорости характеризуется центростремительным (нормальным) ускорением a_n – составляющей полного ускорения a, направленного по нормали к траектории в сторону центра кривизны (см. рис. 192).

Числовое значение нормального ускорения определяется в общем случае по формуле
a_n = v 2 /R,
где v – модуль скорости точки в данный момент;
R – радиус кривизны траектории в месте, где находится точка в данный момент.

После того как определены касательное и нормальное ускорения, легко определить и ускорение a ( полное ускорение точки ).

Так как касательная и нормаль взаимно перпендикулярны, то числовое значение ускорения а можно определить при помощи теоремы Пифагора:
a = sqrt(a_t 2 + a_n 2 ).

Направление вектора a можно определить, исходя из тригонометрических соотношений, по одной из следующих формул:
sin α = a_n/a; cos α = a_t/a; tg α = a_n/a_t.

Но можно сначала определить направление полного ускорения a использовав формулу tg α = a_n/a_t,
а затем найти числовое значение a:
a = a_n/sin α или a = a_t/cos α.

Касательное и нормальное ускорения точки являются главными кинематическими величинами, определяющими вид и особенности движения точки.

Наличие касательного ускорения (a_t≠0) или его отсутствие (a_t=0) определяют соответственно неравномерность или равномерность движения точки.

Наличие нормального ускорения (a_n≠0) или его отсутствие (a_n=0) определяют криволинейность или прямолинейность движения точки.

Движение точки можно классифицировать так:
а) равномерное прямолинейное (a_t = 0 и a_n = 0);
б) равномерное криволинейное (a_t = 0 и a_n ≠ 0);
в) неравномерное прямолинейное (a_t ≠ 0 и a_n = 0);
г) неравномерное криволинейное (a_t ≠ 0 и a_n ≠ 0).

Таким образом, движение точки классифицируется по двум признакам: по степени неравномерности движения и по виду траектории.

Степень неравномерности движения точки задана уравнением s=f(t), а вид траектории задается непосредственно.

§ 27. Равномерное прямолинейное движение точки

Если a_t=0 и a_n=0, то вектор скорости остается постоянным (v=const), т. е. не изменяется ни по модулю, ни по направлению. Такое движение называется равномерным прямолинейным .

Уравнение равномерного движения имеет вид
(а) s = s₀ + vt
или в частном случае, когда начальное расстояние s₀=0,
(б) s = vt.

В уравнение (а) входит всего четыре величины, из них две переменные: s и t и две постоянные: s₀ и v. Поэтому в условии задачи на равномерное и прямолинейное движение точки должны быть заданы три любые величины.

При решении задач необходимо выяснить все заданные величины и привести их к одной системе единиц. При этом нужно заметить, что как в системе МКГСС (технической), так и в СИ единицы всех кинематических величин одинаковы: расстояние s измеряется в м, время t – в сек, скорость v – в м/сек.

§ 28. Равномерное криволинейное движение точки

Если a_t = 0 и a_n ≠ 0, то модуль скорости остается неизменным (точка движется равномерно), но ее направление изменяется и точка движется криволинейно. Иначе, при равномерном движении по криволинейной траектории точка имеет нормальное ускорение, направленное по нормали к траектории и численно равное
a_n = v 2 /R,
где R – радиус кривизны траектории.

В частном случае движения точки по окружности (или по дуге окружности) радиус кривизны траектории во всех ее точках постоянный:
R = r = const,
а так как и числовое значение скорости постоянно, то
a_n = v 2 /r = const.

При равномерном движении числовое значение скорости определяется из формулы
v = (s — s₀)/t или v = s/t.

Если точка совершит полный пробег по окружности, то путь s равен длине окружности, т. е. s = 2πr = πd (d = 2r – диаметр), а время равно периоду, т. е. t = T. Выражение скорости примет вид
v = 2πr/T = πd/T.

§ 29. Равнопеременное движение точки

Если вектор a_t=const (касательное ускорение постоянно как по модулю, так и по направлению), то a_n=0. Такое движение называется равнопеременным и прямолинейным .

Если же постоянным остается только числовое значение касательного уравнения
a_t = dv/dt = f'(t) = const,
то a_n≠0 и такое движение точки называется равнопеременным криволинейным .

При |a_t|>0 движение точки называется равноускоренным , а при |a_t| равнозамедленным .

Уравнение равнопеременного движения независимо от его траектории имеет вид
(1) s = s₀ + v₀t + a_tt 2 / 2.

Здесь s₀ – расстояние точки от исходного положения в момент начала отсчета; v₀ – начальная скорость и a_t – касательное ускорение – величины численно постоянные, a s и t – переменные.

Числовое значение скорости точки в любой момент времени определяется из уравнения
(2) v = v₀ + a_tt.

Уравнения (1) и (2) являются основными формулами равнопеременного движения и они содержат шесть различных величин: три постоянные: s₀, v₀, a_t и три переменные: s, v, t.

Следовательно, для решения задачи на равнопеременное движение точки в ее условии должно быть дано не менее четырех величин (систему двух уравнений можно решить лишь в том случае, если они содержат два неизвестных).

Если неизвестные входят в оба основных уравнения, например, неизвестны a_t и t, то для удобства решения таких задач выведены вспомогательные формулы:

после исключения a_t из (1) и (2)
(3) s = s₀ + (v + v₀)t / 2;

после исключения t из (1) и (2)
(4) s = s₀ + (v 2 — v₀ 2 ) / (2a_t).

В частном случае, когда начальные величины s₀=0 и v₀=0 (равноускоренное движение из состояния покоя), то получаем те же формулы в упрощенном виде:
(5) s = a_tt 2 / 2;
(6) v = a_tt;
(7) s = vt / 2;
(8) s = v 2 / (2a_t).

Уравнения (5) и (6) являются основными, а уравнения (7) и (8) – вспомогательными.

Равноускоренное движение из состояния покоя, происходящее под действием только силы тяжести, называется свободным падением . К этому движению применимы формулы (5)–(8), причем
a_t = g = 9,81 м/сек 2 ≈ 9,8 м/сек 2 .

§ 30. Неравномерное движение точки по любой траектории

§ 31. Определение траектории, скорости и ускорения точки, если закон ее движения задан в координатной форме

Если точка движется относительно некоторой системы координат, то координаты точки изменяются с течением времени. Уравнения, выражающие функциональные зависимости координат движущейся точки от времени, называют уравнениями движения точки в системе координат (см. § 51, п. 2 в учебнике Е. М. Никитина).

Движение точки в пространстве задается тремя уравнениями:
x = f₁(t);
(1) y = f₂(t);
z = f₃(t);

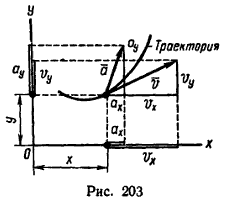
Движение точки в плоскости (рис. 203) задается двумя уравнениями:
(2) x = f₁(t);
y = f₂(t);

Системы уравнений (1) или (2) называют законом движения точки в координатной форме .

Ниже рассматривается движение точки в плоскости, поэтому используется только система (2).

Если закон движения точки задан в координатной форме, то:

а) траектория плоского движения точки выражается уравнением
y = F(x),
которое образуется из данных уравнений движения после исключения времени t;

б) числовое значение скорости точки находится из формулы
v = sqrt(v_x 2 + v_y 2 )
после предварительного определения проекции (см. рис. 203) скорости на оси координат
v_x = dx/dt и v_y = dy/dt;

в) числовое значение ускорения находится из формулы
a = sqrt(a_x 2 + a_y 2 )
после предварительного определения проекций ускорения на оси координат
a_x = dv_x/dt и a_y = dv_y/dt;

г) направления скорости и ускорения относительно осей координат определяются из тригонометрических соотношений между векторами скорости или ускорения и их проекциями.

§ 32. Кинематический способ определения радиуса кривизны траектории

При решении многих технических задач возникает необходимость знать радиус кривизны R (или 1/R – кривизну ) траектории. Если задано уравнение траектории, то радиус ее кривизны в любой точке можно определить при помощи дифференциального исчисления. Используя уравнения движения точки в координатной форме, можно определять радиус кривизны траектории движущейся точки без непосредственного исследования уравнения траектории. Определение радиуса кривизны траектории при помощи уравнений движения точки в координатной форме называется кинематическим способом. Этот способ основан на том, что радиус кривизны траектории движущейся точки входит в формулу
a_n = v 2 /R,
выражающую числовое значение нормального ускорения.

Скорость v точки определяется по формуле
(б) v = sqrt(v_x 2 + v_y 2 ).

Числовое значение нормального ускорения a_n входит в выражение полного ускорения точки
a = sqrt(a_n 2 + a_t 2 ),
откуда
(в) a_n = sqrt(a 2 — a_t 2 ),
где квадрат полного ускорения
(г) a 2 = a_x 2 + a_y 2
и касательное ускорение
(д) a_t = dv/dt.

Таким образом, если закон движения точки задан уравнениями
x = f₁(t);
y = f₂(t),
то при определении радиуса кривизны траектории рекомендуется произвести следующее:

1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:
v_x = f₁‘(t);
v_y = f₂‘(t).

2. Подставив в (б’) выражения v_x и v_y, найти v 2 .

3. Продифференцировав по t уравнение (б), полученное непосредственно из (б’), найти касательное ускорение a_t, а затем a_t 2 .

4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
a_x = f₁»(t) = v_x‘;
a_y = f₂»(t) = v_y‘.

5. Подставив в (г) выражения a_x и a_y, найти a 2 .

6. Подставить в (в) значения a 2 и a_t 2 и найти a_n.

7. Подставив в (а) найденные значения v 2 и a_n, получить радиус кривизны R.