Прямолинейное равнопеременное движение
Содержание:
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково. Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Прямолинейное равнопеременное движение
Равнопеременное прямолинейное движение. Равнопеременным прямолинейным движением называется дви—жение, при котором за любые равные промежутки времени скорость те-ла изменяется на одинаковую величину и траектория – прямая линия.
Средняя скорость неравномерного движения
Большинство движений, наблюдаемых нами в природе и технике,— движения переменные, то есть неравномерные. Таковы, например, движения автомобиля, трактора, поезда, людей, животных и др.
Для характеристики неравномерного движения на каком-нибудь участке пути вводится понятие средней скорости движения.
Рассмотрим пример. Допустим, что расстояние от Москвы до Горького (440 км) поезд прошёл за 11 час. Движение поезда на всём пути было явно неравномерное: он то ускорял движение, то замедлял и даже останавливался на промежуточных станциях. Но если бы путь в 440 км поезд прошёл за 11 час., двигаясь равномерно, то его скорость была бы: 

Средняя скорость неравномерного движения на данном участке пути измеряется отношением длины участка пути к промежутку времени, в течение которого этот путь пройден
Но так же рассчитывается и скорость равномерного движения. Следовательно, можно сказать, что средняя скорость неравномерного движения равна скорости такого равномерного движения, при котором тело проходит тот же путь и за такой же промежуток времени, как и при данном неравномерном движении.
Если известны время и средняя скорость неравномерного движения на некотором участке пути, то длину этого участка пути можно рассчитать по формуле:
Мгновенная скорость
В каждый момент времени тело движется с определённой скоростью, и каждому моменту времени соответствует определённая точка на траектории.
Рис. 32. К понятию мгновенной скорости.
Скорость, которую имеет тело в данный момент времени или в данной точке траектории, называется мгновенной скоростью.
При равномерном движении тела его скорость во всех точках траектории одинакова. Это и будет его мгновенная скорость. Сложнее дело обстоит е случае неравномерного движения.
Допустим, что тело, двигаясь неравномерно-прямолинейно, за t сек. прошло путь АВ — s (рис. 32). Средняя скорость этого движения 
Разобьём весь наш путь АВ на отдельные участки и определим среднюю скорость на участке пути 


Подобные рассуждения можно провести относительно любой точки, взятой на траектории АВ.
Подкрепим теперь наши общие.рассуждения о мгновенной скорости числовыми данными. Допустим, что четыре наблюдателя определяют скорость автомобиля в момент его прохождения мимо какого-нибудь предмета у дороги. С момента прохождения автомобиля мимо этого предмета все наблюдатели одновременно измеряют пути, пройденные автомобилем от этого предмета за различные промежутки времени. Результаты их наблюдений следующие:
Какая же из полученных величин скорости ближе к мгновенной скорости, которую имел автомобиль, проезжая мимо указанного выше предмета?
Рис. 33. Определение мгновенной скорости на опыте.
Такой скоростью, очевидно, будет скорость, вычисленная из результата измерений четвёртого наблюдателя, так как за 3 сек. автомобиль меньше всего изменил свою скорость. Итак, чем меньше взять промежуток времени, тем точнее можно определить искомую скорость тела в заданный момент времени.
Мгновенную скорость можно определить на опыте. Обратимся к рисунку 33. С наклонной плоскости скатывается тележка с капельницей. По отметкам, оставляемым капельницей, легко установить, что тележка движется неравномерно. Допустим, нам нужно определить мгновенную скорость тележки в какой-либо точке наклонной плоскости, например у её основания С. Для этого к наклонной плоскости в точке С присоединим горизонтальный жёлоб СВ,
Пользуясь капельницей; так же как в опыте, описанном на странице 13, легко установить, что когда тележка проходит точку С, то дальше она на небольшом отрезке пути отточки С движется равномерно. Следовательно, скорость в точке Сбудет такой же, как на всём дальнейшем пути равномерного движения. Отмечая время равномерного движения какой-либо точки на тележке и измеряя пройденный ею путь, можно определить скорость равномерного движения; она и будет искомой мгновенной скоростью в точке С.
Для определения мгновенной скорости в какой-либо другой точке А нужно только поднять горизонтальную часть плоскости СВ на уровень точки А и произвести такие же измерения, как и для точки С.
Мгновенные скорости движения автомобиля отмечаются стрелкой на шкале спидометра.
Ускорение
Среди разнообразных переменных движений встречаются движения, в которых скорость непрерывно возрастает. Такие движения называются ускоренными.
Ускоренно, например, движется поезд, отходящий от станции и постепенно увеличивающий свою скорость, поднимающийся в воздух самолёт, пуля в канале ружья и т. д. В сущности начало всякого движения является движением ускоренным, так как всякое тело, начиная двигаться, не мгновенно „набирает“ свою скорость.
В разных ускоренных движениях скорость изменяется по-разному—в одних быстрее, в других медленнее. Сравним, например, движение поезда при отходе со станции с движением снаряда в стволе орудия при выстреле. Оба эти движения ускоренные. Но в то время как скорость поезда возрастает медленно, скорость снаряда за какие-нибудь сотые доли секунды увеличивается от нуля до сотен метров в секунду.
Таким образом, ускоренные движения отличаются одно от другого быстротой изменёния скорости.
Характеристикой быстроты изменения скорости является особая величина, называемая ускорением. Чем быстрее изменяется скорость движения, тем больше величина ускорения.
Обозначим начальную скорость переменного движения тела 


Величина, измеряемая отношением изменения скорости к тому промежутку времени, за которое это изменение произошло, называется ускорением.
Обозначив ускорение буквой а, мы можем написать:

Пусть, например, в некоторый момент времени скорость пули в стволе винтовки была 100 

800 


Ускорение движения пули внутри ствола винтовки будет равно:


Мы узнали, что ускорение движения пули внутри ствола 

Единица ускорения
Установим теперь единицу ускорения. Положив 

Это значит, что единицей ускорения является ускорение такого движения, при котором за единицу времени скорость изменяется на единицу скорости.
Если измерять скорость в 

Приняв за единицу скорости 
Этими двумя единицами чаще всего и измеряют ускорение, но, вообще говоря, за единицу ускорения можно принимать 
Численное значение ускорения, как и любой другой физической величины, зависит от выбора единиц измерения.
П р и м е р. Ускорение некоторого движения равно 
Равноускоренное движение
Познакомимся с ускоренным движением на опыте.
Рис. 34. Положения шарика через равные промежутки времени при его движении по наклонному жёлобу (отмечены флажками).
Установим наклонно жёлоб и предоставим шарику скатываться по нему. Определим пройденные шариком пути за одну, две, три и т. д. секунды. На рисунке 34 положения шарика на жёлобе в конце каждой из этих секунд обозначены флажками и помечены буквами 




Чтобы установить закон возрастания скорости, измерим мгновенные скорости, которые будет иметь центр шарика в конце первой,второй, третьей и т. д. секунды.
Рис. 35. К установлению закона изменения скорости при движении шарика по наклонному жёлобу.
Для этого от нижнего конца наклонного жёлоба вверх по нему (рис. 35) отложим расстояния 



Скатившись с наклонного жёлоба, шарик будет двигаться с разными скоростями, причём во всех случаях на некотором отрезке горизонтального пути движение шарика будет равномерным.
Измерив в каждом случае путь, пройденный шариком по горизонтальной плоскости за 1 сек., мы найдём скорость шарика на участке равномерного движения, т. е. его мгновенную скорость в точке о.
В одном из опытов были получены следующие численные значения мгновенных скоростей шарика:
В этом опыте скорость движения шарика по наклонному жёлобу увеличивалась за 1 сек. на одну и ту же величину (на 20 
Движение, при котором в любые равные промежутки времени скорость увеличивается на одну и ту же величину, называется равноускоренным.
Движение шарика по наклонному жёлобу есть равноускоренное движение.
Равноускоренное движение является одним из простейших видов ускоренных движений. Для равноускоренного движения, как мы увидим, зависимость скорости и пути от времени можно выразить простыми математическими формулами.
Скорость равноускоренного движения
В равноускоренном движении ускорение на всём протяжении пути не меняется, поэтому равноускоренное движение есть движение с постоянным ускорением.
Скорость в равноускоренном движении каждую секунду увеличивается на одну и ту же величину, численно равную ускорению.
Рассмотрим, как можно рассчитать скорость равноускоренного движения в конце какого-нибудь промежутка времени, если известны начальная скорость и ускорение.
Пусть в начале наблюдения скорость тела, например поезда, равна 
Чему будет равна скорость поезда через t секунд?
Нам уже известно, что ускорение равноускоренного движения показывает, на сколько возрастает скорость за каждую секунду.
В нашем примере ускорение равно 

Так как в начале наблюдения скорость поезда была равна 

Если обозначить скорость тела в конце промежутка времени t через 
Что изменится, если начальная скорость будет равной, например, 


Рассуждая по-прежнему, мы получим:

или
Таким образом, алгебраическое выражение для конечной скорости остаётся без изменения. Изменяется только наименование скорости.
Следовательно, конечная скорость равноускоренного движения может быть рассчитана по формуле:
В этой формуле 
Тот же результат можем получить алгебраически из формулы:
о которой говорится в параграфе 19.
Эта формула представляет собой уравнение первой степени. Решим его относительно
Для равноускоренного движения, которое начинается из состояния покоя, 
Значит, если начальная скорость равна нулю, то мгновенная скорость равноускоренного движения пропорциональна времени.
Пользуясь формулой (3), можно значение вычисленных в опыте § 21 скоростей представить в виде следующей таблицы:
Из этой таблицы видно, что скорость движения шарика по наклонному жёлобу в любой момент времени может быть рассчитана но формуле:
График скорости равноускоренного движения
Рис. 36. Оси координат (ось времён и ось скоростей).
Зависимость скорости равноускоренного движения от времени можно выразить не только алгебраически, но и графически. Для этого возьмём две взаимно перпендикулярные оси координат (рис. 36). Одну из них Ov назовём осью скоростей, а другую Ot— осью времён. Перпендикуляр, опущенный из любой какой-нибудь точки А на ось времён, отсекает на ней отрезок ОВ, численно равный (в выбранном масштабе) некоторому промежутку времени t, а перпендикуляр, опущенный из той же точки на ось скоростей, отсекает отрезок ОС, рав
ный по величине скорости в конце этого промежутка времени.
Из построения видно, что расстояние АВ определяет величину скорости в момент времени t.
Построим сначала график движения без начальной скорости. Пусть, например, ускорение 

Начертим оси координат Ov и Ot (рис. 37). На оси времён отложим равные отрезки 0—1. 1—2, 2—3 и т. д., каждый из которых соответствует 1 секунде.
Из концов этих отрезков по данным нашей таблицы (в масштабе 1 см—
График скорости равноускоренного движения имеет такой же вид, как и полученный нами ранее график пути равномерного движения (рис. 37).
Рис. 37. График скорости равноускоренного движения с начальной скоростью, равной нулю.
Рис. 38. График скорости равноускоренного движения с начальной скоростью, не равной нулю.
В обоих случаях график представляет собой прямую, проходящую через начало координат. Эго не случайное совпадение. Дело в том, что пройденный путь при равномерном движении и скорость при равноускоренном движении изменяются по одному и тому же закону—прямо пропорционально времени. Закон же прямой пропорциональности, как это доказывается в математике, графически изображается прямой линией.
Построим теперь график для случая, когда начальная скорость не равна нулю, например 


Отмечая соответствующие точки на графике и соединяя их между собой линией, получим график скорости равноускоренного движения с начальной скоростью (рис. 38). Так как скорость увеличивается в каждую секунду на одну и ту же величину, то линия, соединяющая точки А, В, С, D,—прямая, но она не проходит через точку пересечения осей, так как в момент t = 0 скорость тела не равняется нулю.
Графический способ вывода формулы пути равноускоренного движения
В равномерном движении пройденный путь графически изображался площадью прямоугольника, построенного на графике скорости (§ 11).
Рис. 40. К выводу формулы пути, пройденного при равноускоренном движении.
В равноускоренном же движении с начальной скоростью пройденный путь изображается площадью трапеции. Это мы используем для вывода формулы пути равноускоренного движения.
На рисунке 40 график скорости равноускоренного движения изображён прямой АС. Путь, пройденный за время t, на том же рисунке изображается площадью ОАСВ; он численно равен площади ОАСВ. Эта площадь ограничена отрезком прямой АС, представляющим собой график скорости, отрезками
Из рисунка 40 видно, что если к площади прямоугольника ОАМВ прибавить площадь треугольника АСМ, то мы получим площадь S фигуры ОАСВ. Таким образом,
Но OB = AM = t, 


Для движения без начальной скорости 
По формуле 


Из этой таблицы видно, что за две секунды тело пройдёт путь, в 4 раза больший, чем за первую секунду, за три секунды—в 9 раз больший и т. д., т.е. при равноускоренном движении без начальной скорости пройденный путь пропорционален квадрату времени.
Из формулы 
Средняя скорость равноускоренного движения
Из формулы пути равноускоренного движения легко вывести формулу средней скорости.
Из определения средней скорости следует (см. § 17), что 

а преобразуя правую часть написанного равенства, будем иметь:

Так как 

Итак, средняя скорость равноускоренного движения за некоторый промежуток времени равна полусумме начальной и конечной скоростей.
Для случая, когда
В равноускоренном движении скорость движения изменяется равномерно от 

Уравнения равноускоренного движения
называются уравнениями равноускоренного движения; они выражают зависимость скорости или пути в этом движении от времени.
Этих формул вполне достаточно для решения любой задачи на равноускоренное движение. Однако для упрощения расчётов в задачах, где не дано времени движения, целесообразно пользоваться ещё одной формулой.
Из формулы ускорения (§ 19) время 

Заменяя 


откуда
Если начальная скорость равна нулю: 
Формулами (4) и (5) часто пользуются для решения задач, когда не дано времени движения.
Пути, проходимые в равноускоренном движении за равные последовательные промежутки времени
Воспользуемся таблицей пройденных путей, приведённой на странице 43, и определим пути, проходимые телом в равноускоренном движении без начальной скорости за каждую отдельную секунду.
Пройденный путь за первую секунду от начала движения равен 
Чтобы вычислить путь 
Пройденный путь 
Таким же образом найдём, что пути 
Составим отношение из числовых значений пройденных путей:
Преобразуя правую часть равенства, получим:
Из полученного нами равенства видно, что пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечётных чисел.
Свободное падение тел
Одним из интересных и важных видов движения является движение падающих тел. Изучим это движение на опыте.
Рис. 43. Тело, подвешенное на нити, натягивает нить по вертикали.
Подвесим на нити какое-нибудь тяжёлое тело (рис. 43), нить натянется вдоль определённого направления. Это направление, как известно, называется вертикальным или отвесным, а нить с грузом—отвесом.
Если пережечь нить, тело будет падать по вертикальному направлению.
Выпустим из рук с одинаковой высоты одновременно плашмя металлический кружок и такого же диаметра лёгкий картонный кружок. Мы увидим, что скорее упадёт металлический кружок. Почему? Не является ли причиной этого различие в весе падающих тел?
Такой вывод легко опровергается следующим опытом. Возьмём два одинаковых листа бумаги и, скомкав один из них, уроним оба листа с одинаковой высоты. Мы увидим, что скомканный лист упадёт быстрее. Следовательно, причиной различной скорости падения тел является не только различие в весе тел.
Положим картонный кружок на металлический и выпустим их из рук. Оба кружка упадут в одно и то же время. Этот опыт отличается от первого тем, что условия падения кружков здесь неодинаковы. Металлический кружок, падая, встречает сопротивление воздуха, между тем как для картонного кружка этого препятствия нет: оно устраняется металлическим кружком, падающим впереди картонного. Следовательно, на скорость падения тел влияет сопротивление воздуха.
Рассмотрим теперь, как будут падать тела в отсутствие сопротивления воздуха, в безвоздушном пространстве.
Возьмём стеклянную трубку длиной примерно 1,5 м с одним закрытым концом и с краном на другом конце (рис. 44). В трубку вложены: монета, птичье пёрышко, кусочек пробки, дробинка, т. е. тела разной формы и разного веса. Пока в трубке имеется воздух, упомянутые тела при перевёртывании трубки движутся с разными скоростями. Но стоит только откачать воздух из трубки, и те же тела будут двигаться с одинаковыми скоростями.
Падение тел в безвоздушном пространстве называется свободным падением.
Галилео Галилей (1564— 1642)—великий итальянский учёный, основатель опытной физики.
Галилей открыл законы падения тел и качания маятника, ему принадлежит идея закона инерции, включённого Ньютоном в число основных законов механики. Галилей изобрёл термометр, первый применил телескоп для астрономических исследований, открыл спутников Юпитера, солнечные пятна и фазы Венеры.
Галилей был ревностным пропагандистом взглядов Коперника, за что был судим судом папской инквизиции и под угрозой пыток вынужден был подписать отказ от своих убеждений. Однако на деле он остался верен им и до конца жизни продолжал развивать учение о гелиоцентрической системе мира.
Падение тел опытным путём впервые изучал в конце XVI в. Галилей, роняя тяжёлые тела с башни (рис. 45). Эти опыты показали, что все тела, независимо от их веса, достигали поверхности земли почти в одно и то же время.
Рис. 45. Наклонная башня, которой пользовался Галилей для изучения законов падения тел.
Законы падения Галилей открыл, изучая движение шарика по наклонному жёлобу. Это движение является тоже падением, только протекающим медленнее, чем падение по вертикали.
Исследования Галилея показали, что свободное падение есть движение равноускоренное.
Особенностью свободного падения является то, что все тела в данном месте падают с одинаковым ускорением. Это ускорение называется ускорением свободного падения,
Ускорение свободного падения обозначается буквой (первая буква латинского слова гравитас, что значит тяжесть).
Так как движение свободно падающего тела есть равноускоренное движение без начальной скорости, то расчёты пути и скорости в этом движении производятся по формулам, выведенным в § 22 и 24.
Так, если тело падает с высоты h в течение времени t, то
При этом тело достигает скорости
v = gt или
Величину g можно определить опытным путём, например заставляя стальной шарик падать с определённой высоты и измеряя время падения. Сопротивление воздуха, которое испытывает при этом шарик, незначительно.
При проведении одного такого опыта в пролёте школьной лестницы с высоты 17,6 м падал стальной шарик. Секундомер показал время падения 1,9 сек. По формуле 
Существуют, конечно, способы, позволяющие определить величину g значительно точнее, чем мы это делали в школе.
Численное значение g на разных широтах земного шара различно и колеблется между 

Ускорение свободного падения 
Причины, вызывающие различие в ускорениях свободного падения тел, будут рассмотрены далее.
В расчётах, если не требуется особой точности, пользуются значением g, равным 

Равнозамедленное движение
На рисунке 47 изображено движение шарика от толчка вверх по наклонному жёлобу.

Рис. 47. Движение шарика вверх по наклонному жёлобу.
Флажками отмечены положения шарика через одну, две, три секунды от начала движения. Расстояние между флажками, а следовательно, и пути, проходимые шариком за равные промежутки времени, уменьшаются. Значит, движение шарика замедленное.
Простейшим видом замедленного движения является движение равнозамедленное.
В равнозамедленном движении скорость за любые равные промежутки времени уменьшается на одну и ту же величину.
При этом ускорение, вычисляемое по формуле:
окажется отрицательной величиной, так как 



Равнозамедленное движение есть движение с постоянным отрицательным ускорением.
Чтобы получить формулы скорости и пути для равнозамедленного движения, достаточно в аналогичных формулах равноускоренного движения заменить а на — а.
Тогда формула скорости будет:
для пройденного же пути получим:
Равноускоренное и равнозамедленное движения часто называют равнопеременными движениями, так как в обоих этих движениях скорость изменяется равномерно.
Многие движения весьма близки к равнопеременным и при различных расчётах могут быть приняты за равнопеременные. Так, движения поездов и автомобилей при отходе их от остановки и при торможении, движение пули внутри ствола и многие другие могут рассматриваться как равнопеременные.
Движение тела, брошенного вертикально вверх
Примером замедленного движения (очень близкого к равнозамедленному) может служить движение тела, брошенного вертикально вверх.
Действительно всякое тело свободно падает с ускорением g, направленным вертикально вниз. Вследствие этого при движении тела вертикально вверх его скорость ежесекундно уменьшается на величину, численно равную ускорению свободного падения. Брошенное вертикально вверх тело движется равнозамедленно до тех пор, пока скорость его не станет равной нулю. В этот момент тело достигает наибольшей высоты и с этой высоты начинает свободно падать, двигаясь обратно вниз.
Формулы для подсчёта скорости и пути движения тела, брошенного вертикально вверх, для любого момента времени будут:
где h—высота, на которую поднимается тело за время t.
Формулу для расчёта высоты h можно также получить, рассматривая движение тела, брошенного вертикально вверх, как сложное движение, состоящее из двух движений: из движения равномерного, направленного вертикально вверх с некоторой начальной скоростью, и из свободного падения. Оба движения происходят по одной прямой; поэтому пройденный телом путь за некоторый промежуток времени будет равен алгебраической сумме путей, пройденных в каждом отдельном движении.
Обозначим скорость, с которой тело брошено вертикально вверх, через 



Рассмотрим следующий пример. Пусть тело брошено вертикально вверх со скоростью 

Так как в момент времени, когда тело достигает наибольшей высоты, 

Чтобы определить наибольшую высоту, на которую поднимается тело, подставим найденную величину t в уравнение (2), определяющее h:
Найдём теперь, с какой скоростью тело, падая с этой высоты, вернётся к начальному своему положению. Так как тело, падая, будет двигаться равноускоренно без начальной скорости и пройдёт расстояние h, то скорость его будет равна:
т. е. скорость, с которой тело вернётся в то же место, откуда оно было брошено, равна первоначальной скорости (если не учитывать сопротивления воздуха).
Услуги по физике:
Лекции по физике:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Равнопеременное прямолинейное движение
Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
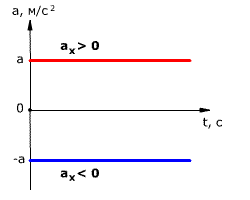
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
Проекция вектора скорости на ось ОХ:
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
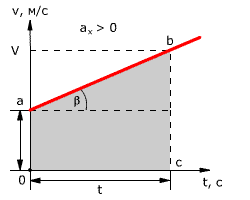
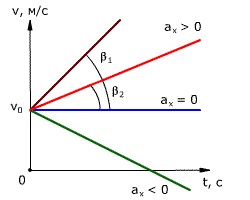
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:
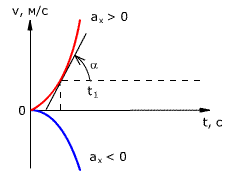
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx
Прямолинейному равнопеременному движению соответствуют уравнения
лЙОЕНБФЙЛБ ЙЪХЮБЕФ ТБЪМЙЮОЩЕ НЕИБОЙЮЕУЛЙЕ ДЧЙЦЕОЙС ФЕМ ВЕЪ ТБУУНПФТЕОЙС РТЙЮЙО ЧЩЪЩЧБАЭЙИ ЬФЙ ДЧЙЦЕОЙС.
1.1.1 лЙОЕНБФЙЛБ РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС
рТЙ РПУФХРБФЕМШОПН ДЧЙЦЕОЙЙ ФЕМБ ЧУЕ ФПЮЛЙ ФЕМБ ДЧЙЦХФУС ПДЙОБЛПЧП, Й, ЧНЕУФП ФПЗП ЮФПВЩ ТБУУНБФТЙЧБФШ ДЧЙЦЕОЙЕ ЛБЦДПК ФПЮЛЙ ФЕМБ, НПЦОП ТБУУНБФТЙЧБФШ ДЧЙЦЕОЙЕ ФПМШЛП ПДОПК ЕЗП ФПЮЛЙ.
пУОПЧОЩЕ ИБТБЛФЕТЙУФЙЛЙ ДЧЙЦЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ: ФТБЕЛФПТЙС ДЧЙЦЕОЙС, РЕТЕНЕЭЕОЙЕ ФПЮЛЙ, РТПКДЕООЩК ЕА РХФШ, ЛППТДЙОБФЩ, УЛПТПУФШ Й ХУЛПТЕОЙЕ.
мЙОЙА, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ Ч РТПУФТБОУФЧЕ, ОБЪЩЧБАФ ФТБЕЛФПТЙЕК.
рЕТЕНЕЭЕОЙЕН НБФЕТЙБМШОПК ФПЮЛЙ ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ОБЪЩЧБЕФУС ЧЕЛФПТ РЕТЕНЕЭЕОЙС ∆r=r-r0, ОБРТБЧМЕООЩК ПФ РПМПЦЕОЙС ФПЮЛЙ Ч ОБЮБМШОЩК НПНЕОФ ЧТЕНЕОЙ Л ЕЕ РПМПЦЕОЙА Ч ЛПОЕЮОЩК НПНЕОФ.
уЛПТПУФШ НБФЕТЙБМШОПК ФПЮЛЙ РТЕДУФБЧМСЕФ УПВПК ЧЕЛФПТ, ИБТБЛФЕТЙЪХАЭЙК ОБРТБЧМЕОЙЕ Й ВЩУФТПФХ РЕТЕНЕЭЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ ПФОПУЙФЕМШОП ФЕМБ ПФУЮЕФБ. чЕЛФПТ ХУЛПТЕОЙС ИБТБЛФЕТЙЪХЕФ ВЩУФТПФХ Й ОБРТБЧМЕОЙЕ ЙЪНЕОЕОЙС УЛПТПУФЙ НБФЕТЙБМШОПК ФПЮЛЙ ПФОПУЙФЕМШОП ФЕМБ ПФУЮЕФБ.
1.1.2 тБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ
тБЧОПНЕТОЩН РТСНПМЙОЕКОЩН ДЧЙЦЕОЙЕН ОБЪЩЧБЕФУС ФБЛПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ, РТЙ ЛПФПТПН НБФЕТЙБМШОБС ФПЮЛБ (ФЕМП) ДЧЙЦЕФУС РП РТСНПК Й Ч МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ УПЧЕТЫБЕФ ПДЙОБЛПЧЩЕ РЕТЕНЕЭЕОЙС.
чЕЛФПТ УЛПТПУФЙ ТБЧОПНЕТОПЗП РТСНПМЙОЕКОПЗП ДЧЙЦЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ ОБРТБЧМЕО ЧДПМШ ЕЕ ФТБЕЛФПТЙЙ Ч УФПТПОХ ДЧЙЦЕОЙС. чЕЛФПТ УЛПТПУФЙ РТЙ ТБЧОПНЕТОПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ ТБЧЕО ЧЕЛФПТХ РЕТЕНЕЭЕОЙС ЪБ МАВПК РТПНЕЦХФПЛ ЧТЕНЕОЙ, РПДЕМЕООПНХ ОБ ЬФПФ РТПНЕЦХФПЛ ЧТЕНЕОЙ:
рТЙНЕН МЙОЙА, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ, ЪБ ПУШ ЛППТДЙОБФ пи, РТЙЮЕН ЪБ РПМПЦЙФЕМШОПЕ ОБРТБЧМЕОЙЕ ПУЙ ЧЩВЕТЕН ОБРТБЧМЕОЙЕ ДЧЙЦЕОЙС ФПЮЛЙ. фПЗДБ, УРТПЕГЙТПЧБЧ ЧЕЛФПТЩ r Й v, ОБ ЬФХ ПУШ, ДМС РТПЕЛГЙК ∆rx = |∆r| Й ∆vx = |∆v| ЬФЙИ ЧЕЛФПТПЧ НЩ НПЦЕН ЪБРЙУБФШ:

ф.Л. РТЙ ТБЧОПНЕТОПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ S = |∆r|, НПЦЕН ЪБРЙУБФШ: Sx = vx · t. фПЗДБ ДМС ЛППТДЙОБФЩ ФЕМБ Ч МАВПК НПНЕОФ ЧТЕНЕОЙ ЙНЕЕН:
ЗДЕ И0 — ЛППТДЙОБФБ ФЕМБ Ч ОБЮБМШОЩК НПНЕОФ t = 0.
рТЙНЕТ 1. хТБЧОЕОЙЕ ДЧЙЦЕОЙС ФЕМБ ДБОП Ч ЧЙДЕ И = 4 — 3t. пРТЕДЕМЙФШ ОБЮБМШОХА ЛППТДЙОБФХ ФЕМБ, УЛПТПУФШ ДЧЙЦЕОЙС Й РЕТЕНЕЭЕОЙС ФЕМБ ЪБ 2 УЕЛХОДЩ.
тЕЫЕОЙЕ: уТБЧОЙН ДБООПЕ ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ФЕМБ У ХТБЧОЕОЙЕН ДЧЙЦЕОЙС Ч ПВЭЕН ЧЙДЕ: И = И0 + vx t Й И = 4 — 3t.
пЮЕЧЙДОП, ЮФП И0 = 4Н, vx = — 3Н/У (ЪОБЛ «-» ПЪОБЮБЕФ, ЮФП ОБРТБЧМЕОЙЕ УЛПТПУФЙ ОЕ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ПУЙ пи, Ф.Е. ПОЙ РТПФЙЧПРПМПЦОП ОБРТБЧМЕОЩ). рЕТЕНЕЭЕОЙЕ ФЕМБ ОБКДЕН РП ЖПТНХМЕ: S = И — И0. лПОЕЮОХА ЛППТДЙОБФХ И НПЦОП ПРТЕДЕМЙФШ, РПДУФБЧМСС Ч ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ЧТЕНС t1: И = 4 — 3t1. ч ПВЭЕН ЧЙДЕ ЖПТНХМБ РЕТЕНЕЭЕОЙС: S = 4 — 3t1 — И0 = 4 — 3t1 — 4 = — 3t1 = -3 · 2 = — 6 Н (фЕМП ДЧЙЦЕФУС Ч ПФТЙГБФЕМШОПН ОБРТБЧМЕОЙЙ ПУЙ пи).
рТЙНЕТ 2.мПДПЮОЙЛ РЕТЕЧПЪЙФ РБУУБЦЙТПЧ У ПДОПЗП ВЕТЕЗБ ОБ ДТХЗПК ЪБ ЧТЕНС t =10 НЙО. РП ФТБЕЛФПТЙЙ бч. уЛПТПУФШ ФЕЮЕОЙС ТЕЛЙ vТ = 0,3 Н/У, ЫЙТЙОБ ТЕЛЙ 240 Н. у ЛБЛПК УЛПТПУФША v ПФОПУЙФЕМШОП ЧПДЩ Й РПД ЛБЛЙН ХЗМПН α Л ВЕТЕЗХ ДПМЦОБ ДЧЙЗБФШУС МПДЛБ, ЮФПВЩ ДПУФЙЮШ ДТХЗПЗП ВЕТЕЗБ ЪБ ХЛБЪБООПЕ ЧТЕНС?
t = 10 НЙО = 660 У.
v’ — ? α — ?

тЕЫЕОЙЕ: рТЙНЕН ВЕТЕЗ ЪБ ОЕРПДЧЙЦОХА УЙУФЕНХ ПФУЮЕФБ. фПЗДБ ПФОПУЙФЕМШОП ВЕТЕЗБ УЛПТПУФШ МПДЛЙ ТБЧОБ:
ьФБ УЛПТПУФШ (ТЙУХОПЛ 1.1), СЧМСЕФУС УХННПК ДЧХИ УЛПТПУФЕК: УЛПТПУФЙ МПДЛЙ ПФОПУЙФЕМШОП ЧПДЩ v’ (УЛПТПУФЙ ПФОПУЙФЕМШОП РПДЧЙЦОПК УЙУФЕНЩ ПФУЮЕФБ) Й УЛПТПУФЙ ТЕЛЙ vТ (УЛПТПУФЙ УБНПК РПДЧЙЦОПК УЙУФЕНЩ ПФУЮЕФБ ПФОПУЙФЕМШОП ОЕРПДЧЙЦОПК). рП ЪБЛПОХ УМПЦЕОЙС УЛПТПУФЕК: v =vТ + v’. фБЛ ЛБЛ РП ХУМПЧЙА ЪБДБЮЙ УЛПТПУФШ МПДЛЙ ПФОПУЙФЕМШОП ВЕТЕЗБ ОБРТБЧМЕОБ ЧДПМШ бч, Б УЛПТПУФШ ТЕЛЙ РЕТРЕОДЙЛХМСТОП бч, ФП УЛПТПУФШ МПДЛЙ ПФОПУЙФЕМШОП ЧПДЩ(РП ФЕПТЕНЕ рЙЖБЗПТБ):
йУЛПНЩК ХЗПМ НПЦОП ОБКФЙ ЙЪ ЧЩТБЦЕОЙС:

пФЧЕФ: v’ = 0.5 Н /У, α = arctg ≈ 53 0 .
1.1.3 оЕТБЧОПНЕТОПЕ ДЧЙЦЕОЙЕ
дЧЙЦЕОЙЕ, РТЙ ЛПФПТПН ЪБ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ФЕМП УПЧЕТЫБЕФ ОЕТБЧОЩЕ РЕТЕНЕЭЕОЙС ОБЪЩЧБАФ ОЕТБЧОПНЕТОЩН ЙМЙ РЕТЕНЕООЩН. уТЕДОЕК УЛПТПУФША vУТ ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА РЕТЕНЕЭЕОЙС ФЕМБ ∆r ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ЬФПНХ РТПНЕЦХФЛХ:
нПДХМШ УТЕДОЕК УЛПТПУФЙ ПРТЕДЕМСЕФУС ЛБЛ ПФОПЫЕОЙЕ РХФЙ ∆S, РТПКДЕООПЗП ФЕМПН ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ, Л ЬФПНХ РТПНЕЦХФЛХ:
оБРТБЧМЕОЙЕ ЧЕЛФПТБ УТЕДОЕК УЛПТПУФЙ vУТ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ∆r (ТЙУХОПЛ 1.2).
рТЙ ОЕПЗТБОЙЮЕООПН ХНЕОШЫЕОЙЙ ∆t, vУТ УФТЕНЙФУС Л РТЕДЕМШОПНХ ЪОБЮЕОЙА, ЛПФПТПЕ ОБЪЩЧБЕФУС НЗОПЧЕООПК УЛПТПУФША. йФБЛ, НЗОПЧЕООБС УЛПТПУФШ v ЕУФШ РТЕДЕМ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОСС УЛПТПУФШ vУТ, ЛПЗДБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ДЧЙЦЕОЙС УФТЕНЙФУС Л ОХМА:
йЪ ЛХТУБ НБФЕНБФЙЛЙ ЙЪЧЕУФОП, ЮФП РТЕДЕМ ПФОПЫЕОЙС РТЙТБЭЕОЙС ЖХОЛГЙЙ Л РТЙТБЭЕОЙА БТЗХНЕОФБ, ЛПЗДБ РПУМЕДОЙК УФТЕНЙФУС Л ОХМА РТЕДУФБЧМСЕФ УПВПК РЕТЧХА РТПЙЪЧПДОХА ЬФПК ЖХОЛГЙЙ РП ДБООПНХ БТЗХНЕОФХ. рПЬФПНХ:
нЗОПЧЕООБС УЛПТПУФШ v ЕУФШ ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС РЕТЧПК РТПЙЪЧПДОПК ТБДЙХУБ — ЧЕЛФПТБ ДЧЙЦХЭЕКУС ФПЮЛЙ РП ЧТЕНЕОЙ. фБЛ ЛБЛ УЕЛХЭБС Ч РТЕДЕМЕ УПЧРБДБЕФ У ЛБУБФЕМШОПК, ФП ЧЕЛФПТ УЛПТПУФЙ v ОБРТБЧМЕО РП ЛБУБФЕМШОПК Л ФТБЕЛФПТЙЙ Ч УФПТПОХ ДЧЙЦЕОЙС (ТЙУХОПЛ 1.2).
рП НЕТЕ ХНЕОШЫЕОЙЕ ∆t РХФШ ∆S ЧУЕ ВПМШЫЕ ВХДЕФ РТЙВМЙЦБФШУС Л |∆r|, РПЬФПНХ НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ:
фБЛЙН ПВТБЪПН, НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ v ТБЧЕО РЕТЧПК РТПЙЪЧПДОПК РХФЙ РП ЧТЕНЕОЙ :
рТЙ ОЕТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФЕМБ ЕЗП УЛПТПУФШ ОЕРТЕТЩЧОП ЙЪНЕОСЕФУС. лБЛ ВЩУФТП ЙЪНЕОСЕФУС УЛПТПУФШ ФЕМБ, РПЛБЪЩЧБЕФ ЧЕМЙЮЙОБ, ЛПФПТБС ОБЪЩЧБЕФУС ХУЛПТЕОЙЕН. уТЕДОЙН ХУЛПТЕОЙЕН ОЕТБЧОПНЕТОПЗП ДЧЙЦЕОЙС Ч ЙОФЕТЧБМЕ ПФ t ДП t + ∆t ОБЪЩЧБЕФУС ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА ЙЪНЕОЕОЙС УЛПТПУФЙ ∆v Л ЙОФЕТЧБМХ ЧТЕНЕОЙ ∆t:
нЗОПЧЕООЩН ХУЛПТЕОЙЕН Б Ч НПНЕОФ ЧТЕНЕОЙ t ВХДЕФ РТЕДЕМ УТЕДОЕЗП ХУЛПТЕОЙС:
фБЛЙН ПВТБЪПН, ХУЛПТЕОЙЕ ∆Б ЕУФШ ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС РЕТЧПК РТПЙЪЧПДОПК УЛПТПУФЙ РП ЧТЕНЕОЙ. ч ДБООПК УЙУФЕНЕ ПФУЮЕФБ ЧЕЛФПТ ХУЛПТЕОЙС НПЦЕФ ВЩФШ ЪБДБО РТПЕЛГЙСНЙ ОБ УППФЧЕФУФЧХАЭЙЕ ЛППТДЙОБФОЩЕ ПУЙ (РТПЕЛГЙСНЙ БИ, БХ, Бz).
уПУФБЧМСАЭБС Бτ ЧЕЛФПТБ ХУЛПТЕОЙС, ОБРТБЧМЕООБС ЧДПМШ ЛБУБФЕМШОПК Л ФТБЕЛФПТЙЙ Ч ДБООПК ФПЮЛЕ, ОБЪЩЧБЕФУС ФБОЗЕОГЙБМШОЩН (ЛБУБФЕМШОЩН) ХУЛПТЕОЙЕН. фБОЗЕОГЙБМШОПЕ ХУЛПТЕОЙЕ ИБТБЛФЕТЙЪХЕФ ЙЪНЕОЕОЙЕ ЧЕЛФПТБ УЛПТПУФЙ РП НПДХМА. чЕЛФПТ Бτ ОБРТБЧМЕО Ч УФПТПОХ ДЧЙЦЕОЙС ФПЮЛЙ РТЙ ЧПЪТБУФБОЙЙ ЕЕ УЛПТПУФЙ (ТЙУХОПЛ 1.3 — Б) Й Ч РТПФЙЧПРПМПЦОХА УФПТПОХ — РТЙ ХВЩЧБОЙЙ УЛПТПУФЙ (ТЙУХОПЛ 1.3 — В).
 Б) |  В) | ||||||
 тЕЫЕОЙЕ: рХУФШ ПУШ пи УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ДЧЙЦЕОЙС РЕТЧПЗП ЧЕМПУЙРЕДЙУФБ, Б ОБЮБМП ЛППТДЙОБФ У ФПЮЛПК O, Ч ЛПФПТПК ПО ОБИПДЙМУС Ч НПНЕОФ ЧТЕНЕОЙ t = 0 (ТЙУХОПЛ 1.4). фПЗДБ ХТБЧОЕОЙС ДЧЙЦЕОЙС ЧЕМПУЙРЕДЙУФБ ФБЛПЧЩ : ч НПНЕОФ ЧУФТЕЮЙ Ч ФПЮЛЕ б: t = t1; x1 = x2. фПЗДБ РПМХЮЙН ТБЧЕОУФЧП:
пРТЕДЕМЙН РЕТЕНЕЭЕОЙЕ ЛБЦДПЗП ДП ЧУФТЕЮЙ. 1.1.5 уЧПВПДОПЕ РБДЕОЙЕ ФЕМ. дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП ЧЕТФЙЛБМШОП ЧЧЕТИуЧПВПДОЩН РБДЕОЙЕН ОБЪЩЧБЕФУС ДЧЙЦЕОЙЕ, ЛПФПТПЕ УПЧЕТЫЙМП ВЩ ФЕМП ФПМШЛП РПД ДЕКУФЧЙЕН УЙМЩ ФСЦЕУФЙ ВЕЪ ХЮЕФБ УПРТПФЙЧМЕОЙС ЧПЪДХИБ. рТЙ УЧПВПДОПН РБДЕОЙЙ ФЕМБ У ОЕВПМШЫПК ЧЩУПФЩ h ПФ РПЧЕТИОПУФЙ ъЕНМЙ (h ≪RЪ, ЗДЕ RЪ — ТБДЙХУ ъЕНМЙ) ПОП ДЧЙЦЕФУС У РПУФПСООЩН ХУЛПТЕОЙЕН g, ОБРТБЧМЕООЩН ЧЕТФЙЛБМШОП ЧОЙЪ. хУЛПТЕОЙЕ g ОБЪЩЧБЕФУС ХУЛПТЕОЙЕН УЧПВПДОПЗП РБДЕОЙС. пОП ПДОП Й ФПЦЕ ДМС ЧУЕИ ФЕМ Й ЪБЧЙУЙФ МЙЫШ ПФ ЧЩУПФЩ ОБД ХТПЧОЕН НПТС Й ПФ ЗЕПЗТБЖЙЮЕУЛПК ЫЙТПФЩ. еУМЙ Ч НПНЕОФ ОБЮБМБ ПФУЮЕФБ ЧТЕНЕОЙ (t0 = 0) ФЕМП ЙНЕМП УЛПТПУФШ v0, ФП РП ЙУФЕЮЕОЙЙ РТПЙЪЧПМШОПЗП РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t = t — t0 УЛПТПУФШ ФЕМБ РТЙ УЧПВПДОПН РБДЕОЙЙ ВХДЕФ: v = v0 + g·t. рХФШ h, РТПКДЕООЩК ФЕМПН Ч УЧПВПДОПН РБДЕОЙЙ, Л НПНЕОФХ ЧТЕНЕОЙ t: нПДХМШ УЛПТПУФЙ ФЕМБ РПУМЕ РТПИПЦДЕОЙС Ч УЧПВПДОПН РБДЕОЙЙ РХФЙ h ОБИПДЙФУС ЙЪ ЖПТНХМЩ: рТПДПМЦЙФЕМШОПУФШ ∆t УЧПВПДОПЗП РБДЕОЙС ВЕЪ ОБЮБМШОПК УЛПТПУФЙ (v0 = 0) У ЧЩУПФЩ h: рТЙНЕТ 1. фЕМП РБДБЕФ ЧЕТФЙЛБМШОП ЧОЙЪ У ЧЩУПФЩ 20 Н ВЕЪ ОБЮБМШОПК УЛПТПУФЙ. пРТЕДЕМЙФШ: 1) РХФШ h, РТПКДЕООЩК ФЕМПН ЪБ РПУМЕДОАА УЕЛХОДХ РБДЕОЙС, 2) УТЕДОАА УЛПТПУФШ РБДЕОЙС vУТ, 3) УТЕДОАА УЛПТПУФШ ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ vУТ2. |  тЕЫЕОЙЕ: оБРТБЧЙН ПУШ Х ЧЕТФЙЛБМШОП ЧОЙЪ, Й РХУФШ ОБЮБМП ЛППТДЙОБФ УПЧРБДБЕФ У ОБЮБМШОЩН РПМПЦЕОЙЕН ФЕМБ (ТЙУХОПЛ 1.5). 1) уПЗМБУОП ЖПТНХМЕ: ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ЪБРЙЫЕФУС Ч ЧЙДЕ: Ч НПНЕОФ РБДЕОЙС ОБ ЪЕНМА Х = h0. пФУАДБ ЧТЕНС ДЧЙЦЕОЙС ФЕМБ: ъБ ЧТЕНС ( t — ∆t) ФЕМП РТПЫМП РХФШ рХФШ ЪБ РПУМЕДОАА УЕЛХОДХ ТБЧЕО: 2) фЕМП РТПЫМП РХФШ h0. чТЕНС ДЧЙЦЕОЙС
3) дМС ПРТЕДЕМЕОЙС УТЕДОЕК УЛПТПУФЙ ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ, ОЕПВИПДЙНП ХЪОБФШ ЧТЕНС, ЪБ ЛПФПТПЕ ЬФБ ЮБУФШ РХФЙ РТПКДЕОБ. чТЕНС ДЧЙЦЕОЙС ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ ТБЧОП РПМОПНХ ЧТЕНЕОЙ РПМЕФБ t НЙОХУ ЧТЕНС t1, ЪБФТБЮЕООПЕ ОБ РТПИПЦДЕОЙЕ РЕТЧПК РПМПЧЙОЩ РХФЙ. чТЕНС t1 ОБИПДЙФУС ЙЪ ХТБЧОЕОЙС: | ,Ф.Е. |  |
 |
 |
рТЙ ДЧЙЦЕОЙЙ ФЕМБ ЧЕТФЙЛБМШОП ЧЧЕТИ У ОБЮБМШОПК УЛПТПУФША v0, ХУЛПТЕОЙЕ ФЕМБ ТБЧОП ХУЛПТЕОЙА УЧПВПДОПЗП РБДЕОЙС g. оБ ХЮБУФЛЕ ДП ОБЙЧЩУЫЕК ФПЮЛЙ РПДЯЕНБ ДЧЙЦЕОЙЕ ФЕМБ СЧМСЕФУС ТБЧОПЪБНЕДМЕООЩН, Б РПУМЕ ДПУФЙЦЕОЙС ЬФПК ФПЮЛЙ — УЧПВПДОЩН РБДЕОЙЕН ВЕЪ ОБЮБМШОПК УЛПТПУФЙ.
уЛПТПУФШ ФЕМБ Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t ПФ ОБЮБМБ ДЧЙЦЕОЙС ОЕЪБЧЙУЙНП ПФ ФПЗП, ТБУУНБФТЙЧБЕФУС МЙЫШ РПДЯЕН ФЕМБ ЙМЙ ЕЗП ПРХУЛБОЙЕ РПУМЕ ДПУФЙЦЕОЙС ОБЙЧЩУЫЕК ФПЮЛЙ, ТБЧОБ v = v0 + g·t.
чЕЛФПТ РЕТЕНЕЭЕОЙС ∆r ФЕМБ ЪБ РТПЙЪЧПМШОЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t0, РТЙ ХУМПЧЙЙ t0 = 0, ТБЧЕО:
ч НПНЕОФ ЧТЕНЕОЙ tРПД, УППФЧЕФУФЧХАЭЙК ОБЙВПМШЫЕНХ РПДЯЕНХ ФЕМБ ОБД ФПЮЛПК ВТПУБОЙС (ЛПЗДБ Х = ХНБИ ЙМЙ ЧЩУПФБ РПДЯЕНБ ФЕМБ НБЛУЙНБМШОБ h = hmax = Хmax — Х0) УЛПТПУФШ ФЕМБ УФБОЕФ ТБЧОБ ОХМА: v = v0 — g·tРПД = 0, ПФЛХДБ tРПД = v0/g, Ч ЬФПФ НПНЕОФ ОБРТБЧМЕОЙЕ ДЧЙЦЕОЙС ФЕМБ ЙЪНЕОСЕФУС ОБ РТПФЙЧПРПМПЦОПЕ.
нБЛУЙНБМШОБС ЧЩУПФБ РПДЯЕНБ ФЕМБ ОБД ФПЮЛПК ВТПУБОЙС:
1.1.6 дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП РПД ХЗМПН Л ЗПТЙЪПОФХ Й ВТПЫЕООПЗП ЗПТЙЪПОФБМШОП У ОЕЛПФПТПК ЧЩУПФЩ
дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП У ОЕЛПФПТПК ЧЩУПФЩ, НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ ОЕЪБЧЙУЙНЩИ ДЧЙЦЕОЙС: ТБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ, РТПЙУИПДСЭЕЕ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ УП УЛПТПУФША υИ , ТБЧОПК ОБЮБМШОПК УЛПТПУФЙ ВТПУБОЙС υ0 (υИ = υ0), Й УЧПВПДОПЕ РБДЕОЙЕ У ЧЩУПФЩ, ОБ ЛПФПТПК ОБИПДЙМПУШ ФЕМП Ч НПНЕОФ ВТПУБОЙС, У ХУЛПТЕОЙЕН g. дМС ПРЙУБОЙС ЬФПЗП ДЧЙЦЕОЙС ЧЩВЙТБАФ РТСНПХЗПМШОХА УЙУФЕНХ ЛППТДЙОБФ ИпХ. фТБЕЛФПТЙС ДЧЙЦЕОЙС СЧМСЕФУС ЧЕФЧШ РБТБВПМЩ (ТЙУХОПЛ 1.6).
хТБЧОЕОЙЕ ДЧЙЦЕОЙС РП ПУСН пИ Й пХ:
уЛПТПУФШ ФЕМБ Ч МАВПК ФПЮЛЕ ФТБЕЛФПТЙЙ НПЦОП ПРТЕДЕМЙФШ РП ЖПТНХМЕ:
рТЙ ЬФПН ЧТЕНС РПМЕФБ УЧСЪБОП У ЧЕТФЙЛБМШОПК УПУФБЧМСАЭЕК ДЧЙЦЕОЙС. дБМШОПУФШ РПМЕФБ — У ЗПТЙЪПОФБМШОПК.
рТЙНЕТ 1. у ВБЫОЙ ЧЩУПФПК о = 25 Н ЗПТЙЪПОФБМШОП ВТПЫЕО ЛБНЕОШ УП УЛПТПУФША υ0 = 15 Н/У. оБКФЙ: УЛПМШЛП ЧТЕНЕОЙ ЛБНЕОШ ВХДЕФ Ч ДЧЙЦЕОЙЙ; ОБ ЛБЛПН ТБУУФПСОЙЙ Sx ПФ ПУОПЧБОЙЙ ВБЫОЙ ПО ХРБДЕФ ОБ ЪЕНМА; У ЛБЛПК УЛПТПУФША υ ПО ХРБДЕФ ОБ ЪЕНМА; ЛБЛПК ХЗПМ φ УПУФБЧЙФ ФТБЕЛФПТЙС ЛБНОС У ЗПТЙЪПОФПН Ч ФПЮЛЕ ЕЗП РБДЕОЙС ОБ ЪЕНМА.
рЕТЕНЕЭЕОЙЕ ВТПЫЕООПЗП ЗПТЙЪПОФБМШОП ЛБНОС НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ (ТЙУХОПЛ 1.7): ЗПТЙЪПОФБМШОПЕ Sx Й ЧЕТФЙЛБМШОПЕ Sy.
рТЙНЕОСС ЪБЛПО ОЕЪБЧЙУЙНПУФЙ ДЧЙЦЕОЙС, ЙНЕЕН:


1)

2) Sx = L = v0·t = 15 · 2,26 = 33,9 Н;
3) vХ = g · t = 9,81 · 2,26 = 22,1 Н/У,
4)

дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП РПД ХЗМПН Л ЗПТЙЪПОФХ, ФБЛЦЕ НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ ОЕЪБЧЙУЙНЩИ ДЧЙЦЕОЙС: ТБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ, РТПЙУИПДСЭЕЕ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ У ОБЮБМШОПК УЛПТПУФША v0И = v0·Cosα Й УЧПВПДОПЕ РБДЕОЙЕ У ОБЮБМШОПК УЛПТПУФША v0Х = v0·Sinα, (ТЙУХОПЛ 1.8). зДЕ α — ХЗПМ НЕЦДХ ОБРТБЧМЕОЙСНЙ ЧЕЛФПТБ УЛПТПУФЙ υ0 Й ПУША пИ. фТБЕЛФПТЙЕК ФБЛПЗП ДЧЙЦЕОЙС СЧМСЕФУС РБТБВПМБ. хТБЧОЕОЙС ДЧЙЦЕОЙС РТЙНХФ ЧЙД:
уЛПТПУФШ ФЕМБ Ч МАВПК ФПЮЛЕ ФТБЕЛФПТЙЙ:
рТЙНЕТ 2. фЕМП ВТПЫЕОП РПД ХЗМПН α Л ЗПТЙЪПОФХ У ОБЮБМШОПК УЛПТПУФША υ0. пРТЕДЕМЙФШ ЧТЕНС РПМЕФБ t, НБЛУЙНБМШОХА ЧЩУПФХ о РПДЯЕНБ Й ДБМШОПУФШ L РПМЕФБ.
тЕЫЕОЙЕ: лБЛ ПВЩЮОП ЪБДБЮБ ОБЮЙОБЕФУС У ЧЩСЧМЕОЙС УЙМ, ДЕКУФЧХАЭЙИ ОБ ФЕМП. оБ ФЕМП ДЕКУФЧХЕФ ФПМШЛП УЙМБ ФСЦЕУФЙ, РПЬФПНХ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ ПОП РЕТЕНЕЭБЕФУС ТБЧОПНЕТОП, Б Ч ЧЕТФЙЛБМШОПН — ТБЧОПРЕТЕНЕООП У ХУЛПТЕОЙЕН g.
вХДЕН ТБУУНБФТЙЧБФШ ЧЕТФЙЛБМШОХА Й ЗПТЙЪПОФБМШОХА УПУФБЧМСАЭЙЕ ДЧЙЦЕОЙС ФЕМБ РП ПФДЕМШОПУФЙ, ДМС ЬФПЗП ТБЪМПЦЙН ЧЕЛФПТ ОБЮБМШОПК УЛПТПУФЙ ОБ ЧЕТФЙЛБМШОХА ( υ0·Sinα ) Й ЗПТЙЪПОФБМШОХА ( υ0·Cosα ) УПУФБЧМСАЭЙЕ (ТЙУХОПЛ 1.9).
оБЮОЕН ТБУУНБФТЙЧБФШ ЧЕТФЙЛБМШОХА УПУФБЧМСАЭХА ДЧЙЦЕОЙС. чТЕНС РПМЕФБ t = t1 + t2, ЗДЕ t1 — ЧТЕНС РПДЯЕНБ (ФЕМП ДЧЙЦЕФУС РП ЧЕТФЙЛБМЙ ТБЧОПЪБНЕДМЕООП), t2 — ЧТЕНС УРХУЛБ (ФЕМП ДЧЙЦЕФУС РП ЧЕТФЙЛБМЙ ТБЧОПХУЛПТЕООП).
чЕТФЙЛБМШОБС УЛПТПУФШ ФЕМБ Ч ОБЙЧЩУЫЕК ФПЮЛЕ ФТБЕЛФПТЙЙ (РТЙ t = t1) ТБЧОБ ПЮЕЧЙДОП ОХМА. у ДТХЗПК УФПТПОЩ, ЬФБ УЛПТПУФШ НПЦЕФ ВЩФШ ЧЩТБЦЕОБ РТЙ РПНПЭЙ ЖПТНХМЩ ЪБЧЙУЙНПУФЙ УЛПТПУФЙ ТБЧОПЪБНЕДМЕООПЗП ДЧЙЦЕОЙС ПФ ЧТЕНЕОЙ.
пФУАДБ, РПМХЮБЕН: 0 = υ0Sinα — g·t1 ЙМЙ
рПДУФБЧЙН (1.1) Ч (1.2)
чТЕНС УРХУЛБ t2 НПЦОП ЧЩЮЙУМЙФШ, ТБУУНПФТЕЧ РБДЕОЙЕ ФЕМБ У ЙЪЧЕУФОПК ЧЩУПФЩ о ВЕЪ ОБЮБМШОПК ЧЕТФЙЛБМШОПК УЛПТПУФЙ:
рПМОПЕ ЧТЕНС РПМЕФБ:
дМС ОБИПЦДЕОЙС ДБМШОПУФЙ РПМЕФБ L ОЕПВИПДЙНП ПВТБФЙФШУС Л ЗПТЙЪПОФБМШОПК УПУФБЧМСАЭЕК ДЧЙЦЕОЙС ФЕМБ. лБЛ ХЦЕ ПФНЕЮБМПУШ, РП ЗПТЙЪПОФБМЙ ФЕМП РЕТЕНЕЭБЕФУС ТБЧОПНЕТОП.
1.1.7 тБЧОПРЕТЕНЕООПЕ ДЧЙЦЕОЙЕ ФПЮЛЙ РП ПЛТХЦОПУФЙ
дЧЙЦЕОЙЕ РП ПЛТХЦОПУФЙ СЧМСЕФУС РТПУФЕКЫЙН РТЙНЕТПН ЛТЙЧПМЙОЕКОПЗП ДЧЙЦЕОЙС. уЛПТПУФШ υ ДЧЙЦЕОЙС РП ПЛТХЦОПУФЙ ОБЪЩЧБЕФУС МЙОЕКОПК (ПЛТХЦОПК) УЛПТПУФША. рТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ РП ПЛТХЦОПУФЙ НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ НБФЕТЙБМШОПК ФПЮЛЙ У ФЕЮЕОЙЕН ЧТЕНЕОЙ ОЕ ЙЪНЕОСЕФУС. дЧЙЦХЭБСУС ФПЮЛБ ЪБ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ РТПИПДЙФ ТБЧОЩЕ РП ДМЙОЕ ДХЗЙ ПЛТХЦОПУФЙ. фБОЗЕОГЙБМШОПЕ ХУЛПТЕОЙЕ РТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФПЮЛЙ РП ПЛТХЦОПУФЙ ПФУХФУФЧХЕФ ( aτ ). йЪНЕОЕОЙЕ ЧЕЛФПТБ УЛПТПУФЙ υ РП ОБРТБЧМЕОЙА ИБТБЛФЕТЙЪХЕФУС ОПТНБМШОЩН ХУЛПТЕОЙЕН an, ЛПФПТПЕ ОБЪЩЧБЕФУС ФБЛЦЕ ГЕОФТПУФТЕНЙФЕМШОЩН ХУЛПТЕОЙЕН.
ч ЛБЦДПК ФПЮЛЕ ФТБЕЛФПТЙЙ ЧЕЛФПТ an ОБРТБЧМЕО РП ТБДЙХУХ Л ГЕОФТХ ПЛТХЦОПУФЙ, Б ЕЗП НПДХМШ ТБЧЕО:
рТЙ ПРЙУБОЙЙ НЕИБОЙЮЕУЛПЗП ДЧЙЦЕОЙС, Ч ЮБУФОПУФЙ ДЧЙЦЕОЙС РП ПЛТХЦОПУФЙ, ОБТСДХ У РТСНПХЗПМШОПК ДЕЛБТФПЧПК УЙУФЕНПК ЛППТДЙОБФ ЙУРПМШЪХЕФУС РПМСТОБС УЙУФЕНБ ЛППТДЙОБФ. рПМПЦЕОЙЕ ФПЮЛЙ н ОБ ЛБЛПК-ФП РМПУЛПУФЙ (ОБРТЙНЕТ, ипх) ПРТЕДЕМСЕФУС ДЧХНС РПМСТОЩНЙ ЛППТДЙОБФБНЙ: НПДХМЕН r ТБДЙХУБ ЧЕЛФПТБ ФПЮЛЙ Й ХЗМПН φ — ХЗМПЧПК ЛППТДЙОБФПК, ЙМЙ РПМСТОЩН ХЗМПН (ТЙУХОПЛ 1.10).
хЗПМ φ ПФУЮЙФЩЧБЕФУС ПФ ПУЙ пи ДП ТБДЙХУБ-ЧЕЛФПТБ r РТПФЙЧ ЮБУПЧПК УФТЕМЛЙ. фПЮЛХ п Ч ЬФПН УМХЮБЕ ОБЪЩЧБАФ РПМАУПН УЙУФЕНЩ ЛППТДЙОБФ. уПЧНЕУФЙН РПМАУ ЛППТДЙОБФ УЙУФЕНЩ У ГЕОФТПН ПЛТХЦОПУФЙ, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ; ФПЗДБ r = R (ТЙУХОПЛ 1.11), Б ЙЪНЕОЕОЙЕ РПМПЦЕОЙС ФПЮЛЙ ОБ ПЛТХЦОПУФЙ НПЦЕФ ВЩФШ ПИБТБЛФЕТЙЪПЧБОП ЙЪНЕОЕОЙЕН ∆φ ХЗМПЧПК ЛППТДЙОБФЩ ФПЮЛЙ: ∆φ = φ2 -φ1.
хЗПМ ∆φ ОБЪЩЧБЕФУС ХЗМПН РПЧПТПФБ ТБДЙХУБ — ЧЕЛФПТБ ФПЮЛЙ. ьМЕНЕОФБТОЩЕ (ВЕУЛПОЕЮОП НБМЩЕ) ХЗМЩ РПЧПТПФБ ТБУУНБФТЙЧБАФУС ЛБЛ ЧЕЛФПТЩ.
нПДХМШ ЧЕЛФПТБ dφ ТБЧЕО ХЗМХ РПЧПТПФБ. оБРТБЧМЕОЙЕ ЧЕЛФПТБ dφ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС ПУФТЙС ЧЙОФБ, ЗПМПЧЛБ ЛПФПТПЗП, ЧТБЭБЕФУС Ч ОБРТБЧМЕОЙЙ ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ, Ф.Е. РПДЮЙОСЕФУС РТБЧЙМХ РТБЧПЗП ЧЙОФБ (ТЙУХОПЛ 1.12).
CТЕДОЕК ХЗМПЧПК УЛПТПУФША ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ ЧПЛТХЗ ПУЙ ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ ωcp, ТБЧОБС ПФОПЫЕОЙА ХЗМБ РПЧПТПФБ ∆φ ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ДМЙФЕМШОПУФЙ ЬФПЗП РТПНЕЦХФЛБ:
хЗМПЧПК УЛПТПУФША (НЗОПЧЕООПК ХЗМПЧПК УЛПТПУФША) ω ОБЪЩЧБЕФУС РТЕДЕМ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОСС ХЗМПЧБС УЛПТПУФШ РТЙ ВЕУЛПОЕЮОПН ХНЕОШЫЕОЙЙ РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t, ЙМЙ РЕТЧБС РТПЙЪЧПДОБС ПФ ХЗМБ РПЧПТПФБ РП ЧТЕНЕОЙ:
чЕЛФПТ ω ОБРТБЧМЕО ЧДПМШ ПУЙ ЧТБЭЕОЙС РП РТБЧЙМХ РТБЧПЗП ЧЙОФБ, Ф.Е. ФБЛЦЕ ЛБЛ Й dφ (ТЙУХОПЛ 1.13).
рТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФПЮЛЙ РП ПЛТХЦОПУФЙ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ХЗМЩ РПЧПТПФБ ЕЕ ТБДЙХУ-ЧЕЛФПТБ ПДЙОБЛПЧЩ. уМЕДПЧБФЕМШОП, РТЙ ФБЛПН ДЧЙЦЕОЙЙ НЗОПЧЕООБС ХЗМПЧБС УЛПТПУФШ ТБЧОБ УТЕДОЕК ХЗМПЧПК УЛПТПУФЙ: ω = ωcp. хЗПМ РПЧПТПФБ ∆ω ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ, ТБЧОПНЕТОП ДЧЙЦХЭЕКУС РП ПЛТХЦОПУФЙ, ТБЧЕО:
рТПНЕЦХФПЛ ЧТЕНЕОЙ ф, Ч ФЕЮЕОЙЙ ЛПФПТПЗП ФПЮЛБ УПЧЕТЫБЕФ ПДЙО РПМОЩК ПВПТПФ РП ПЛТХЦОПУФЙ, ОБЪЩЧБЕФУС РЕТЙПДПН ПВТБЭЕОЙС (РЕТЙПДПН ЧТБЭЕОЙС), Б ЧЕМЙЮЙОБ υ, ПВТБФОБС РЕТЙПДХ:

ЮБУФПФПК ПВТБЭЕОЙС (ЮБУФПФПК ЧТБЭЕОЙС). ъБ ПДЙО РЕТЙПД ХЗПМ РПЧПТПФБ ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ ТБЧЕО 2π ТБД, РПЬФПНХ 2π = ωT, ПФЛХДБ T = 2π/ω, ЙМЙ ω = 2π/ф = 2πν.
мЙОЕКОБС υ Й ХЗМПЧБС ω УЛПТПУФЙ УЧСЪБОЩ УППФОПЫЕОЙЕН: υ = ω·R. ьФП ЧЙДОП ЙЪ УМЕДХАЭЕЗП ЧЩЧПДБ:
рТЙНЕТ 1. пРТЕДЕМЙФШ НПДХМШ УЛПТПУФЙ Й ГЕОФТПУФТЕНЙФЕМШОПЗП ХУЛПТЕОЙС ФПЮЕЛ ЪЕНОПК РПЧЕТИОПУФЙ ОБ ЬЛЧБФПТЕ. тБДЙХУ ъЕНМЙ РТЙОСФШ ТБЧОЩН 6400 ЛН.
R = 6400 ЛН = 6,4·10 6 Н;
ф = 24 Ю = 8,64·10 4 У;
тЕЫЕОЙЕ: фПЮЛЙ ЪЕНОПК РПЧЕТИОПУФЙ ОБ ЬЛЧБФПТЕ ДЧЙЦХФУС РП ПЛТХЦОПУФЙ ТБДЙХУБ R, РПЬФПНХ НПДХМШ ЙИ УЛПТПУФЙ:
пФЧЕФ: υ = 465 Н/У, БГУ = 0,034 Н /У 2 .
1.1.8 чТБЭБФЕМШОПЕ ДЧЙЦЕОЙЕ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ОЕРПДЧЙЦОПК ПУЙ
дМС ЛЙОЕНБФЙЮЕУЛПЗП ПРЙУБОЙС ЧТБЭБФЕМШОПЗП ДЧЙЦЕОЙС БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ЛБЛПК-ФП ОЕРПДЧЙЦОПК ПУЙ ЙУРПМШЪХАФУС ФЕ ЦЕ ЧЕМЙЮЙОЩ (Й ХТБЧОЕОЙС УЧСЪЙ НЕЦДХ ОЙНЙ), ЮФП Й ДМС ПРЙУБОЙС ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ. рТЙ ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ОЕРПДЧЙЦОПК ПУЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t ХЗМЩ РПЧПТПФБ ТБДЙХУ-ЧЕЛФПТПЧ ТБЪМЙЮОЩИ ФПЮЕЛ ФЕМБ ПДЙОБЛПЧЩ. хЗПМ РПЧПТПФБ ∆φ, УТЕДОСС ωcp Й НЗОПЧЕООБС ω ХЗМПЧЩЕ УЛПТПУФЙ ИБТБЛФЕТЙЪХАФ ЧТБЭБФЕМШОПЕ ДЧЙЦЕОЙЕ ЧУЕЗП БВУПМАФОП ФЧЕТДПЗП ФЕМБ Ч ГЕМПН.
мЙОЕКОБС УЛПТПУФШ υ ЛБЛПК-МЙВП ФПЮЛЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ РТПРПТГЙПОБМШОП ТБУУФПСОЙА R ФПЮЛЙ ПФ ПУЙ ЧТБЭЕОЙС:
рТЙ ТБЧОПНЕТОПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ХЗМЩ РПЧПТПФБ ФЕМБ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ПДЙОБЛПЧЩ ( ∆φ = const ) Й НЗОПЧЕООБС ХЗМПЧБС УЛПТПУФШ ФЕМБ ТБЧОБ УТЕДОЕК ХЗМПЧПК УЛПТПУФЙ ( ω = ωcp ). фБОЗЕОГЙБМШОЩЕ ХУЛПТЕОЙС aτ Х ТБЪМЙЮОЩИ ФПЮЕЛ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ПФУХФУФЧХАФ ( aτ = 0 ), Б ОПТНБМШОПЕ (ГЕОФТПУФТЕНЙФЕМШОПЕ ) ХУЛПТЕОЙЕ an ЛБЛПК-МЙВП ФПЮЛЙ ФЕМБ ЪБЧЙУЙФ ПФ ЕЕ ТБУУФПСОЙС R ДП ПУЙ ЧТБЭЕОЙС:
чЕЛФПТ an ОБРТБЧМЕО Ч ЛБЦДЩК НПНЕОФ ЧТЕНЕОЙ РП ТБДЙХУХ ФТБЕЛФПТЙЙ ФПЮЛЙ Л ПУЙ ЧТБЭЕОЙС.
рТЙ ОЕТБЧОПНЕТОПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ХЗМЩ РПЧПТПФБ ФЕМБ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ОЕПДЙОБЛПЧЩ. хЗМПЧБС УЛПТПУФШ ФЕМБ ω У ФЕЮЕОЙЕН ЧТЕНЕОЙ ЙЪНЕОСЕФУС.
уТЕДОЙН ХЗМПЧЩН ХУЛПТЕОЙЕН εУТ Ч РТПНЕЦХФЛЕ ЧТЕНЕОЙ ∆t = t2 — t1 ОБЪЩЧБЕФУС ЖЙЪЙЮЕУЛБС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА ЙЪНЕОЕОЙС ХЗМПЧПК УЛПТПУФЙ ∆ω = ω2 — ω1 ЧТБЭБАЭЕЗПУС ФЕМБ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ДМЙФЕМШОПУФЙ ЬФПЗП РТПНЕЦХФЛБ:
еУМЙ ХЗМПЧБС УЛПТПУФШ ЪБ РТПЙЪЧПМШОЩЕ ПДЙОБЛПЧЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ЙЪНЕОСЕФУС ПДЙОБЛПЧП ( ∆ω12 = ∆ω34 Й Ф.Д.), ФП εУТ = const (ТБЧОПРЕТЕНЕООПЕ ЧТБЭЕОЙЕ).
хЗМПЧЩН ХУЛПТЕОЙЕН (НЗОПЧЕООЩН ХЗМПЧЩН ХУЛПТЕОЙЕН) ЧТБЭБАЭЕЗПУС ФЕМБ Ч НПНЕОФ ЧТЕНЕОЙ t ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ ε, ТБЧОБС РТЕДЕМХ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОЕЕ ХЗМПЧПЕ ХУЛПТЕОЙЕ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ПФ t ДП t + ∆t РТЙ ВЕУЛПОЕЮОПН ХНЕОШЫЕОЙЙ ∆t, ЙМЙ, ХЗМПЧПЕ ХУЛПТЕОЙЕ — ЬФП РЕТЧБС РТПЙЪЧПДОБС ПФ ХЗМПЧПК УЛПТПУФЙ РП ЧТЕНЕОЙ ЙМЙ ЧФПТБС РТПЙЪЧПДОБС ПФ ХЗМБ РПЧПТПФБ РП ЧТЕНЕОЙ:
йЪНЕОЕОЙЕ ∆ω ХЗМПЧПК УЛПТПУФЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t0 РТЙ ТБЧОПРЕТЕНЕООПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ У ХЗМПЧЩН ХУЛПТЕОЙЕН ε: ∆ω = ε·∆t = ε(t — t0). еУМЙ РТЙ t0 = 0 ОБЮБМШОБС ХЗМПЧБС УЛПТПУФШ ФЕМБ ТБЧОБ ω0, ФП Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t ХЗМПЧБС УЛПТПУФШ ФЕМБ ВХДЕФ ω = ω0 + ε·t.
хЗПМ РПЧПТПФБ ∆φ ФЕМБ ЧПЛТХЗ ПУЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t0 РТЙ ТБЧОПРЕТЕНЕООПН ДЧЙЦЕОЙЙ:
фБОЗЕОГЙБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС:

оПТНБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС:
фБЛЙН ПВТБЪПН, УЧСЪШ НЕЦДХ МЙОЕКОЩНЙ Й ХЗМПЧЩНЙ ЧЕМЙЮЙОБНЙ ЧЩТБЦБЕФУС УМЕДХАЭЙНЙ ЖПТНХМБНЙ: S = R·φ, υ = ω·R, aτ = R·ε, an = ω 2 ·R.
http://av-mag.ru/physics/index.php/mechanics/kinematika/rectilinear-movement/
http://cde.osu.ru/demoversion/course120/2_0.html















































































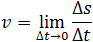
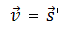

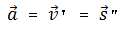

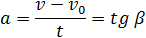
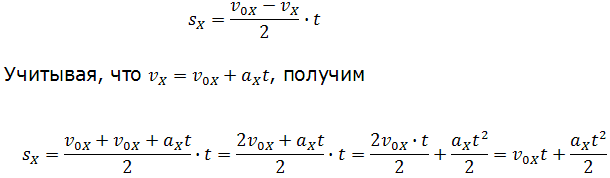
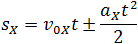
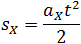
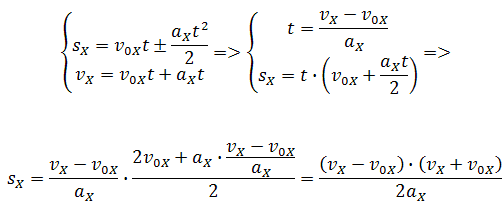
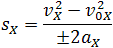
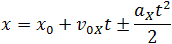


























 (Ф.Л. Б1И= — Б1; И01 = 0);
(Ф.Л. Б1И= — Б1; И01 = 0); (Ф.Л. v2x = — v02 Й a2x = — a2).
(Ф.Л. v2x = — v02 Й a2x = — a2). , ПФЛХДБ v01·t1 + v02·t1 = И02, Ф.Л. Б1 = Б2,
, ПФЛХДБ v01·t1 + v02·t1 = И02, Ф.Л. Б1 = Б2,


















































