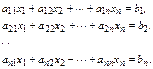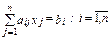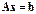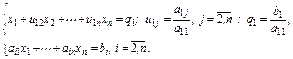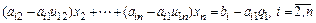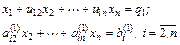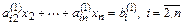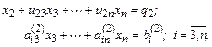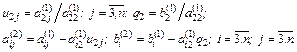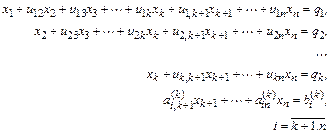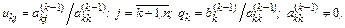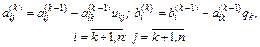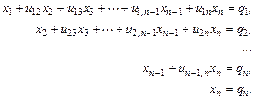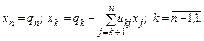Прямые методы решения СЛАУ
Дата добавления: 2013-12-23 ; просмотров: 17145 ; Нарушение авторских прав
Методы решения СЛАУ
Методы решения СЛАУ делятся на две группы:
– прямые (точные) методы;
– итерационные (приближенные) методы.
К прямымметодам относятся такие методы, которые в предположении, что вычисления ведутся без округлений, позволяют получить точные значения неизвестных. Они просты, универсальны и используются для широкого класса систем. Однако они не применимы к системам больших порядков (n –1 :
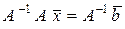
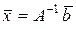
При реализации данного метода стоит проблема нахождения обратной матрицы А –1 , выбора экономичной схемы ее получения и достижения приемлемой точности.
Метод Гаусса. Этот метод является наиболее распространенным методом решения СЛАУ. В его основе лежит идея последовательного исключения неизвестных, в основном приводящая исходную систему к треугольному виду, в котором все коэффициенты ниже главной диагонали равны нулю.
Существуют различные вычислительные схемы, реализующие этот метод. Наибольшее распространение получили схемы с выбором главного элемента либо по строке, либо по столбцу, либо по всей матрице. С точки зрения простоты реализации, хотя и с потерей точности, перед применением этих схем целесообразно использовать так называемую схему единственного деления. Рассмотрим ее суть.
Посредством первого уравнения системы (2.1) исключается х1 из последующих уравнений. Далее посредством второго уравнения исключается х2 из последующих уравнений и т. д. Этот процесс называется прямым ходом Гаусса. Исключение неизвестных повторяется до тех пор, пока в левой части последнего n-го уравнения не останется одно неизвестное хn:
где a¢nn и b¢ – коэффициенты, полученные в результате линейных (эквивалентных) преобразований.
Прямой ход реализуется по формулам
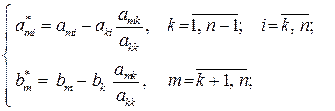
где m – номер уравнения, из которого исключается xk; i – номер столбца исходной матрицы; k – номер неизвестного, которое исключается из оставшихся (n – k) уравнений и обозначает номер уравнения, с помощью которого исключается xk; akk – главный (ведущий) элемент матрицы.
Во время счета необходимо следить, чтобы akk ¹ 0. В противном случае прибегают к перестановке строк матрицы.
Обратный ход метода Гаусса состоит в последовательном вычислении xn, xn–1, . x1, начиная с (2.5) по алгоритму:
xn = b¢ / a¢nn ; 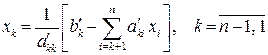
Точность полученного решения оценивается посредством невязки (2.3). В векторе невязки (r1, r2, . rn) Т отыскивается максимальный элемент и сравнивается с заданной точностью e. Приемлемым решение будет, если rmax Т корня 

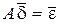
где 
Таким образом, решив линейную систему с прежней матрицей А и новым свободным членом 
Пример решения СЛАУ по методу Гаусса (с точностью до трех знаков). Нужно уточнить корни до 10 –4 :
В результате 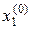


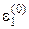

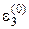
Получено уточнение 


Невязки будут равны d1 = −2×10 –4 ; d2 = −2×10 –4 ; d3 = 0.
Модифицированный метод Гаусса. В данном случае, помимо соблюдения требования akk ¹ 0, при реализации формул (2.6) накладываются дополнительные требования: ведущий (главный) элемент в текущем столбце в процессе преобразований исходной матрицы должен иметь максимальное по модулю значение, что достигается перестановкой строк матрицы.
Пример. В качестве иллюстрации преимущества модифицированного метода Гаусса рассмотрим систему третьего порядка:
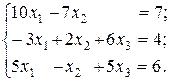
Прямой ход метода Гаусса. Исключаем х1 из второго и третьего уравнений (2.8). Для этого первое уравнение умножаем на 0,3 и складываем со вторым, а затем умножаем первое уравнение на (–0,5) и складываем с третьим. В результате получаем
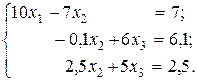
Замена второго уравнения третьим не производится, так как вычисления выполняются в рамках точной арифметики.
Умножив второе уравнение на 25 и сложив с третьим, получим
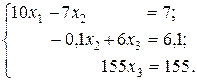
Обратный ход метода Гаусса. Выполняем вычисления начиная с последнего уравнения в полученной системе:
Подставляя полученное решение [0; –1; 1] в исходную систему (2.8), убеждаемся в его истинности.
Теперь изменим коэффициенты системы таким образом, чтобы сохранить прежнее решение, но при вычислении будем использовать округления в рамках арифметики с плавающей точкой, сохраняя пять разрядов. Изменению вычислений будет соответствовать следующая система:

Прямой ход метода для системы (2.8в) повторим по аналогичной технологии с исходной системой (2.8):

После исключения х2 третье уравнение примет вид (остальные – без изменения):
Выполнив обратный ход, получим
Очевидно, что полученные решения [0; –1; 1] и [–0,35; –1,4; 0,99993] различны. Причиной этого является малая величина ведущего элемента во втором уравнении преобразования (2.8г). Чтобы это исключить, переставим в (2.8г) вторую и третью строки:
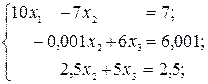

Система (2.8е) после исключения х2 из третьего уравнения примет следующий вид:
В данном случае, выполнив обратный ход:
получим решение системы (2.8в) [0; –1; 1], которое в точности совпадает с решением исходной системы.
Решая систему (2.8г), мы использовали модифицированный метод Гаусса, при выполнении которого на диагонали должен был находиться максимальный в текущем столбце элемент.
Рассмотрим блок-схему модифицированного метода Гаусса (рис. 2.1). Проведем анализ предложенной схемы на примере системы n = 3 (e = 0,001):

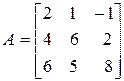
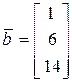
Блок 1. Ввод исходных данных: n – порядок системы, A – матрица коэффициентов при неизвестных, 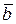
Блок 2. Цикл I прямого хода (для k, изменяющегося от единицы до предпоследнего значения, т. е. до n – 1) обеспечивает исключение из главной диагонали матрицы А элемента akk = 0 благодаря поиску максимального элемента akk в текущем столбце, осуществляемому в блоках 3 — 6 с помощью цикла II.
Далее с помощью цикла III в блоках 7 — 13 выполняется перестановка текущей строки и строки с максимальным элементом в k-м столбце (ее номер р).
Затем реализуются расчеты по формулам (2.6) прямого хода Гаусса в блоках циклов IV и V.
Проведем поблочный анализ в среде рассмотренных циклов I — V на примере (2.9).
Выход из цикла II и вход в цикл III:
В данном случае на диагонали оказался максимальный элемент, поэтому перестановка 2-й и 3-й строк не выполняется.
Выход из цикла III и выполнение блоков 11 – 13:
Свободный член b2 остается на своем месте.
Вход во вложенный цикл V:
Выход из циклов V и IV и завершение (выход) цикла I.
Выполнение обратного хода метода Гаусса:
В блоках 19 — 24 реализуются формулы (2.7). В блоке 19 из последнего уравнения (2.7) находится значение xn (n = 3):
Вход в цикл VI (блок 20), в котором значение переменной цикла k изменяется от n – 1 до 1 с шагом (–1):
Вход в цикл VII (блок 22):
Выход из цикла VII в блок 24 цикла VI:
Далее по аналогии:
Выход из последнего цикла VII.
В блоке 25 (цикл опущен) выполняется вывод на экран полученного решения СЛАУ – вектора 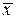
Метод прогонки. Данный метод является модификацией метода Гаусса для частного случая разреженных систем – систем с матрицей трехдиагонального типа (краевая задача дифференциальных уравнений).
Каноническая форма их записи:
aixi–1 + bixi + cixi+1 = di; i = 
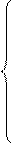
При этом, как правило, все коэффициенты bi ¹ 0.
Метод реализуется в два этапа – прямой и обратный ходы.
посредством прогоночных коэффициентов Ai и Bi. Определим алгоритм их вычисления.
Из первого уравнения системы (2.11) находим x1:

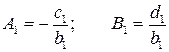
Из второго уравнения системы (2.11) определяем x2 через x3, подставляя найденное значение x1:

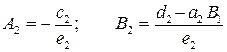
Ориентируясь на соотношения индексов при коэффициентах (2.12) и (2.12а), можно получить эти соотношения для общего случая:

Обратный ход.Из последнего уравнения системы (2.11) с использованием (2.12) при i = n – 1:
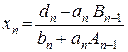
Далее посредством (2.12) и прогоночных коэффициентов (2.13), (2.14) последовательно вычисляем xn – 1, xn – 2, . x1.
При реализации метода прогонки нужно учитывать, что при выполнении условия
или хотя бы для одного bi имеет место строгое неравенство (2.16), деление на ноль исключается и система имеет единственное решение.
Заметим, что условие (2.16) является достаточным, но не необходимым. В ряде случаев для хорошо обусловленных систем (2.11) метод прогонки может быть устойчивым и при несоблюдении условия (2.16).
Схема алгоритма метода прогонки может иметь вид, представленный на рис. 2.2.
Метод квадратного корня. Данный метод используется для решения линейной системы

Решение системы (2.17) осуществляется в два этапа.
Прямой ход. Преобразование матрицы А и представление ее в виде произведения двух взаимно транспонированных треугольных матриц:
Перемножив S Т и S и приравняв матрице А, получим следующие формулы для определения sij:

После нахождения матрицы S систему (2.17) заменяем двумя ей эквивалентными системами с треугольными матрицами (2.18):

Обратный ход. Записываем системы (2.20) в развернутом виде:
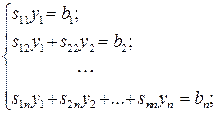

Используя (2.21) и (2.22), последовательно находим:
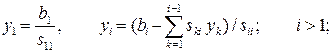

Метод квадратного корня дает большой выигрыш во времени по сравнению с рассмотренными ранее прямыми методами, так как, во-первых, существенно уменьшает число умножений и делений (почти в два раза), во-вторых, позволяет накапливать сумму произведений без записи промежуточных результатов. Числовой пример ручного счета рассмотрен в [1].
Машинная реализация метода квадратного корня предусматривает его следующую трактовку.
Исходная матрица А системы (2.17) представляется в виде произведения трех матриц:
где S T – транспонированная нижняя треугольная матрица; D – диагональная матрица с элементами dii = ±1; S – верхняя треугольная (sik = 0, если i > k , причем sii > 0).
Выполнение условия sii > 0 необходимо для полной определенности разложения. Это и определяет необходимость введения диагональной матрицы D.
Рассмотрим алгоритм разложения матрицы А с использованием матрицы D на примере матрицы второго порядка.
Пусть А – действительная симметричная матрица:
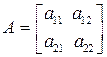
Будем искать S и D в виде


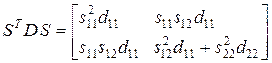
Из условия равенства A = S Т D S получим три уравнения:
Из первого уравнения находим
d11 = sign a11; s11 = 
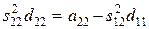
т. е. d22 = sign (a22 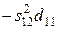
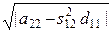
Здесь, как и для общего случая, матрицу S можно по аналогии с числами трактовать как корень квадратный из матрицы А, отсюда и название метода.
Итак, если S Т DS известно, то решение исходной системы 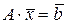

Нахождение элементов матрицы S (извлечение корня из А) выполняем по рекуррентным формулам, что исключает использование комплексных чисел:
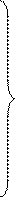

skk = 
skj = 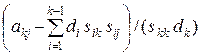
В (2.25) сначала полагаем k = 1 и последовательно вычисляем
d1 = sign (a11); s11 =
и все элементы первой строки матрицы S (s1j, j > 1), затем полагаем k = 2, вычисляем s22 и вторую строку матрицы s1j для j > 2 и т. д.
Решение систем (2.24а) ввиду треугольности матрицы S осуществляется по формулам, аналогичным обратному ходу метода Гаусса:
Метод квадратного корня почти вдвое эффективнее метода Гаусса, так как использует симметричность матрицы.
Схема алгоритма метода квадратного корня представлена на рис. 2.3. Значение функции sign(x) равно +1 для всех х > 0 и –1 для всех x
| | | следующая лекция ==> | |
| Основные понятия и определения | | | Итерационные методы решения СЛАУ |
Не нашли то, что искали? Google вам в помощь!
Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
Содержание:
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 



Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 

Тогда СЛАУ можно записать в матричном виде 





Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 


Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 
Если 
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 


Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Прямые и итерационные методы.
Часть 2. системЫ линейных
АлгебраичЕских уравнений
Лекция 2
ЦЕЛЬ ЛЕКЦИИ: Определить два класса численных методов (прямые и итерационные); показать, как строятся прямые методы Гаусса, LU-факторизации, Холесского; выполнить оценку их эффективности.
Постановка задачи.
Основная задача вычислительной алгебры – решение систем линейных алгебраических уравнений (СЛАУ)
В дальнейшем будем использовать запись этой системы в компактной форме:
( запись 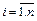
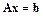
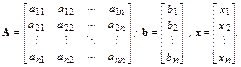 |
где
Предполагается, что матрица 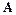
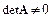
Прямые и итерационные методы.
Численные методы решения СЛАУ делятся на две большие группы: прямые и итерационные.
Прямые методы при отсутствии ошибок округления за конечное число арифметических операций позволяют получить точное решение 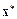
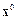
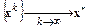
где k – номер итерации. В действительности итерационный процесс прекращается, как только 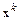
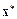
Имеется промежуточный класс методов, в которых решение ищется итерационно, однако для них заранее известно, какое число итераций необходимо выполнить, чтобы в отсутствии ошибок округления получить точное решение. На практике при вычислении приближенного решения число итераций в наиболее эффективных методах оказывается значительно меньшим, чем этого требует теория точного решения.
Какой класс методов лучше? Однозначно на этот вопрос ответить нельзя. Итерационные методы привлекательнее с точки зрения объема вычислений и требуемой памяти, когда решаются системы с матрицами высокой размерности. При небольших порядках системы используют прямые методы либо прямые методы в сочетании с итерационными методами.
Метод Гаусса.
В методе Гаусса линейная система
решается в два этапа. На первом этапе система 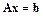
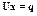
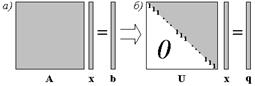 |
Рис. 2.1. Структура системы и портрет ее ненулевых элементов до (а) и после (б)
прямого хода Гаусса
где 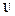
называемый прямой ход Гаусса). На втором этапе (обратный ход Гаусса) решается система 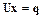
Прямой ход. Прямой ход Гаусса состоит из n шагов.
Первый шаг. Полагаем, что 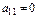
Умножим первое уравнение на 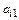
Обозначим 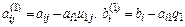
Второй шаг. На втором шаге из системы
исключается 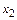
K-й шаг. Запишем общий вид преобразованной системы после k-го шага прямого хода Гаусса:
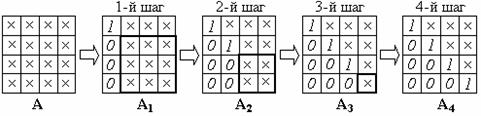
Проиллюстрируем, как меняется матрица системы в процессе прямого хода Гаусса на примере системы четвертого порядка (рис. 2.2; ненулевые элементы матрицы обозначены крестиками).
Рис. 2.2. Преобразование матрицы системы 4-го порядка на прямом ходе Гаусса
Оценим количество длинных операций (умножений и делений) на первом шаге прямого хода Гаусса. Преобразование первого уравнения требует n таких операций. Преобразование остальных n-1 уравнений – n(n-1) операций умножения и деления. Таким образом, первый шаг выполняется за 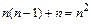
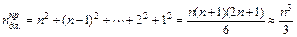
Последняя оценка имеет место для n>>1.
Обратный ход. Запишем систему, решаемую на обратном ходе, в координатном виде
Запись 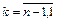
Требуемое число длинных операций на обратном ходе
Приближенная оценка справедлива для n>>1.
Общие затраты метода Гаусса:
Таким образом, при больших n основные затраты в методе Гаусса приходятся на прямой ход.
Дата добавления: 2015-11-24 ; просмотров: 2530 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://www.evkova.org/metodyi-resheniya-sistem-linejnyih-algebraicheskih-uravnenij-slau
http://helpiks.org/6-1.html


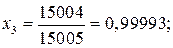
















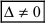 ), то система имеет единственное решение;
), то система имеет единственное решение;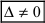 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 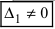 или
или 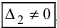 , или, . или
, или, . или 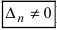 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);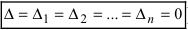 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.