Прямые заданные уравнениями пересекаются скрещиваются

Точка пересечения прямых в пространстве онлайн

С помощю этого онлайн калькулятора можно найти точку пересечения прямых в пространстве. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Точка пересечения прямых в пространстве − теория, примеры и решения

• Содержание
• 1. Точка пересечения прямых, заданных в каноническом виде.
• 2. Точка пересечения прямых, заданных в параметрическом виде.
• 3. Точка пересечения прямых, заданных в разных видах.
• 4. Примеры нахождения точки пересечения прямых в пространстве.

1. Точка пересечения прямых в пространстве, заданных в каноническом виде.

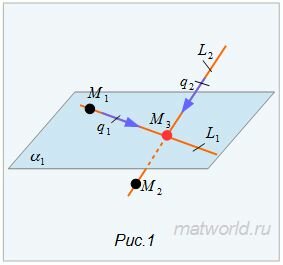
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L₁ и L₂:

,

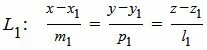(1)

,

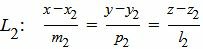(2)

Найти точку пересечения прямых L₁ и L₂ (Рис.1).

Запишем уравнение (1) в виде системы двух линейных уравнений:

,

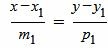(3)

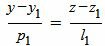(4)

Сделаем перекрестное умножение в уравнениях (3) и (4):

p1(x−x1)=m1(y−y1)

l1(y−y1)=p1(z−z1)

Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

p1x−m1y=p1x1−m1y1,

(5)

l1y−p1z=l1y1−p1z1.

(6)

Аналогичным образом преобразуем уравнение (2):

Запишем уравнение (2) в виде системы двух линейных уравнений:

,

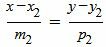(7)

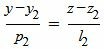(8)

Сделаем перекрестное умножение в уравнениях (7) и (8):

p2(x−x2)=m2(y−y2)

l2(y−y2)=p2(z−z2)

Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

p2x−m2y=p2x2−m2y2,

(9)

l2y−p2z=l2y2−p2z2.

(10)

Решим систему линейных уравнений (5), (6), (9), (10) с тремя неизвестными x, y, z. Для этого представим эту систему в матричном виде:

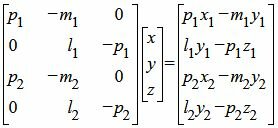(11)

Как решить систему линейных уравнений (11)(или (5), (6), (9), (10)) посмотрите на странице Метод Гаусса онлайн. Если система линейных уравнениий (11) несовместна, то прямые L₁ и L₂ не пересекаются. Если система (11) имеет множество решений, то прямые L₁ и L₂ совпадают. Единственное решение системы линейных уравнений (11) указывает на то, что это решение определяет координаты точки пересечения прямых L₁ и L₂ .

2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L₁ и L₂ в параметрическом виде:

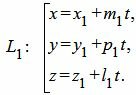(12)

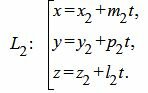(13)

Задачу нахождения нахождения точки пересечения прямых L₁ и L₂ можно решить разными методами.

Метод 1. Приведем уравнения прямых L₁ и L₂ к каноническому виду.

Для приведения уравнения (12) к каноническому виду, выразим параметр t через остальные переменные:

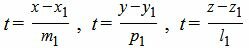(14)

Так как левые части уравнений (14) равны, то можем записать:

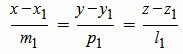(15)

Аналогичным образом приведем уравнение прямой L₂ к каноническому виду:

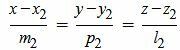(16)

Далее, для нахождения точки пересечения прямых, заданных в каноническом виде нужно воспользоваться параграфом 1.

Метод 2. Для нахождения точки пересечения прямых L₁ и L₂ решим совместно уравнения (12) и (13). Из уравнений (12) и (13) следует:

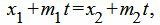(17)

(18)

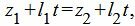(19)

Из каждого уравнения (17),(18),(19) находим переменную t. Далее из полученных значений t выбираем те, которые удовлетворяют всем уравнениям (17)−(19). Если такое значение t не существует, то прямые не пересекаются. Если таких значений больше одного, то прямые совпадают. Если же такое значение t единственно, то подставляя это зачение t в (12) или в (13), получим координаты точки пересечения прямых (12) и (13).

3. Точка пересечения прямых в пространстве, заданных в разных видах.

Если уравнения прямых заданы в разных видах, то можно их привести к одному виду (к каноническому или к параметрическому) и найти точку пересечения прямых, описанных выше.

4. Примеры нахождения точки пересечения прямых в пространстве.

Пример 1. Найти точку пересечения прямых L₁ и L₂:

(20)

(21)

Представим уравнение (20) в виде двух уравнений:

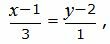(22)

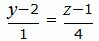(23)

Сделаем перекрестное умножение в уравнениях (22) и (23):

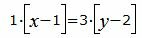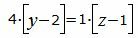Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

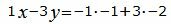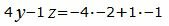Аналогичным образом поступим и с уравнением (2).

Представим уравнение (2) в виде двух уравнений:

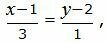(26)

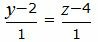(27)

Сделаем перекрестное умножение в уравнениях (7) и (8)

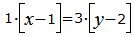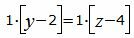Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

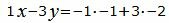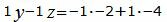Решим систему линейных уравнений (24), (25), (28), (29) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:

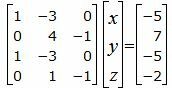(30)

Решим систему линейных уравнений (30) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

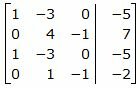Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строку 3 со строкой 1, умноженной на −1:

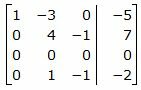Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 4 со строкой 2, умноженной на −1/4:

Сделаем перестановку строк 3 и 4.

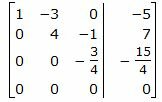Второй этап. Обратный ход Гаусса.

Исключим элементы 3-го столбца матрицы выше элемента a₃₃. Для этого сложим строку 2 со строкой 3, умноженной на −4/3:

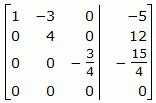Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на 3/4:

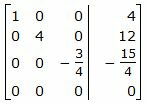Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

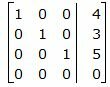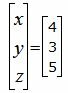Ответ. Точка пересечения прямых L₁ и L₂ имеет следующие координаты:

Пример 2. Найти точку пересечения прямых L₁ и L₂:

(31)

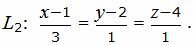(32)

Приведем параметрическое уравнение прямой L₁ к каноническому виду. Выразим параметр t через остальные переменные:

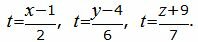Из равентсв выше получим каноническое уравнение прямой:

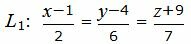(33)

Представим уравнение (33) в виде двух уравнений:

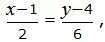(34)

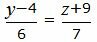(35)

Сделаем перекрестное умножение в уравнениях (34 и (35):

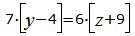Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

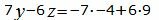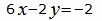(36)

.

(37)

Аналогичным образом поступим и с уравнением (2).

Представим уравнение (2) в виде двух уравнений:

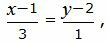(38)

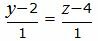(39)

Сделаем перекрестное умножение в уравнениях (38) и (39)

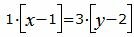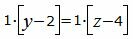Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

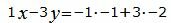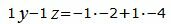Решим систему линейных уравнений (36), (37), (40), (41) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:

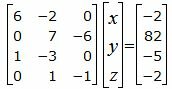(42)

Решим систему линейных уравнений (42) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строку 3 со строкой 1, умноженной на −1/6:

Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строки 3 и 4 со строкой 2, умноженной на 8/21 и −1/7, соответственно:

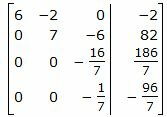Исключим элементы 3-го столбца матрицы ниже элементаa₃₃. Для этого сложим строку 4 со строкой 3, умноженной на -1/16:

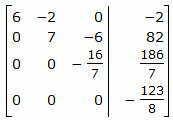Из расширенной матрицы восстановим последнюю систему линейных уравнений:

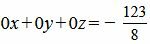(43)

Уравнение (43) несовместна, так как несуществуют числа x, y, z удовлетворяющие уравнению (43). Следовательно система линейных уравнений (42) не имеет решения. Тогда прямые L₁ и L₂ не пересекаются. То есть они или параллельны, или скрещиваются.

Прямая L₁ имеет направляющий вектор q₁=<2,6,7>, а прямая L₂ имеет направляющий вектор q₂=<3,1,1>. Эти векторы не коллинеарны. Следовательно прямые L₁ и L₂ скрещиваются .

Скрещивающиеся прямые. Проведение через одну из скрещивающихся прямых плоскости, параллельной другой прямой

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим определение скрещивающихся прямых и докажем теорему – признак скрещивающихся прямых. Далее рассмотрим три случая взаимного расположения двух прямых в пространстве. Докажем теорему о том, что через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.
В конце урока решим несколько задач в тетраэдре на скрещиваемость прямых.

Взаимное расположение двух прямых в пространстве.
Признак скрещивающихся прямых.
Угол между скрещивающимися прямыми

Взаимное расположение двух прямых в пространстве

Признак скрещивающихся прямых

Угол между скрещивающимися прямыми

Взаимное расположение двух прямых в пространстве

Все возможные случаи взаимного расположения двух прямых в пространстве представлены в следующей таблице.

Фигура	Рисунок	Определение
Две пересекающиеся прямые		Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.
Две параллельные прямые		Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек
Две скрещивающиеся прямые		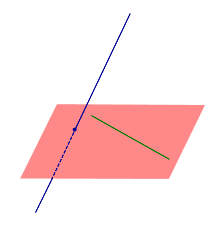Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые.

Две пересекающиеся прямые

Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.

Две параллельные прямые

Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек

Две скрещивающиеся прямые

Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые.

С перечисленными в предыдущей таблице случаями взаимного расположения двух прямых в пространстве близко связаны утверждения, представленные в следующей таблице.

Фигура	Рисунок	Тип утверждения и формулировка
Две различные точки		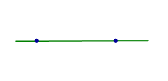Аксиома о прямой линии, заданной двумя точками Через две различные точки проходит одна и только одна прямая линия.
Прямая линия и точка, не лежащая на этой прямой		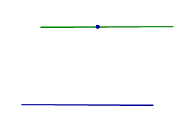Аксиома о параллельных прямых Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.
Две пересекающиеся прямые		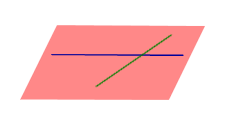Теорема о плоскости, определяемой двумя пересекающимися прямыми Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.
Две параллельные прямые		Теорема о плоскости, определяемой двумя параллельными прямыми Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Две различные точки

Аксиома о прямой линии, заданной двумя точками
Через две различные точки проходит одна и только одна прямая линия.

Прямая линия и точка, не лежащая на этой прямой

Аксиома о параллельных прямых
Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.

Две пересекающиеся прямые

Теорема о плоскости, определяемой двумя пересекающимися прямыми
Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Две параллельные прямые

Теорема о плоскости, определяемой двумя параллельными прямыми
Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Признак скрещивающихся прямых

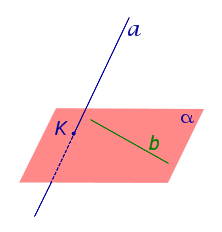
Признак скрещивающихся прямых . Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).

Доказательство . Напомним, что две прямые называют скрещивающимися, если не существует плоскости, содержащей обе эти прямые, и будем доказывать признак скрещивающихся прямых методом «От противного».

Для этого предположим, что прямая a , пересекающая плоскость в точке K , и прямая b , лежащая в плоскости α (рис. 1), не являются скрещивающимися. Из этого предположения следует, что существует плоскость, содержащая обе эти прямые. Обозначим эту плоскость буквой β и докажем, что плоскость β совпадает с плоскостью α . Действительно, поскольку обе плоскости α и β проходят через прямую b и точку K , не лежащую на этой прямой, то они совпадают. Следовательно, прямая a лежит в плоскости прямая a лежит в плоскости . Мы получили противоречие с тем, что по условию прямая a пересекает плоскость прямая a пересекает плоскость , а не лежит в ней. Доказательство признака скрещивающихся прямых завершено.

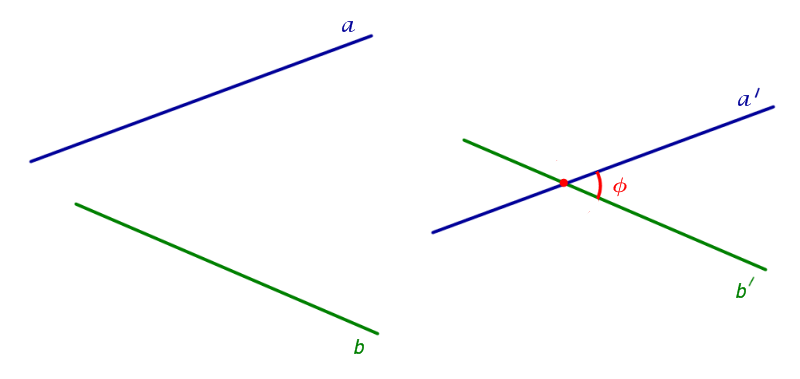
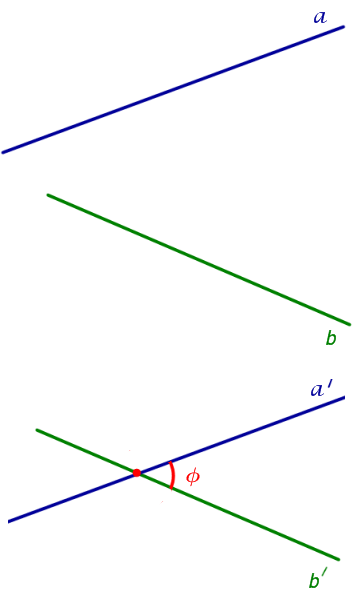
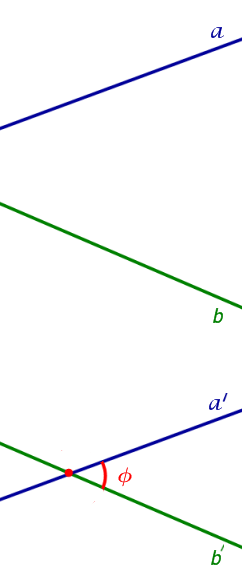
Угол между скрещивающимися прямыми

На рисунке 2 изображены скрещивающиеся прямые a и b . Прямая a’ параллельна прямой a , прямая b’ параллельна прямой b. Прямые a’ и b’ пересекаются. Угол φ и является углом между скрещивающимися прямыми a и b .

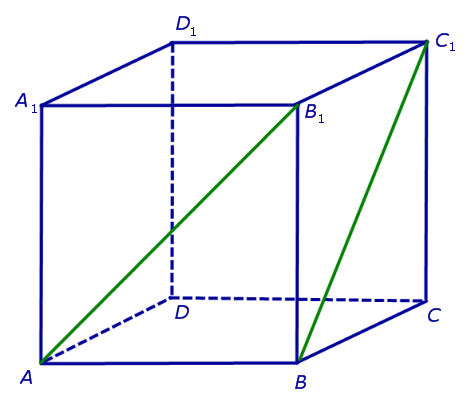
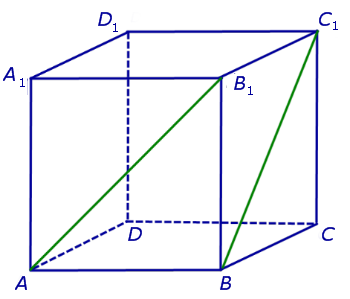
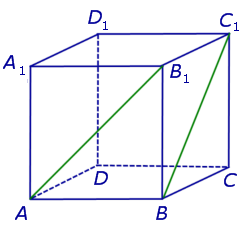
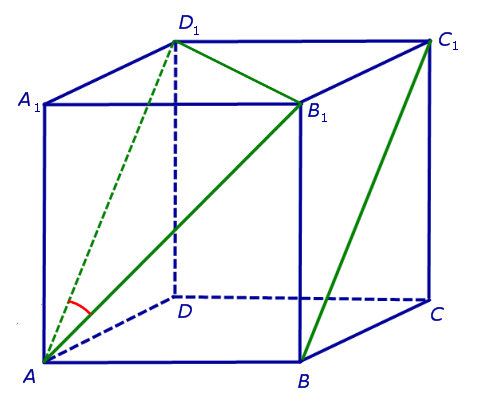
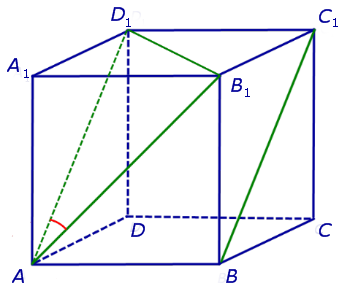
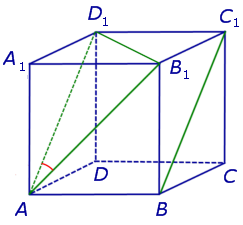
Для того, чтобы найти угол между прямыми AB₁ и BC₁ , проведем в кубе диагональ боковой грани AD₁ и диагональ верхнего основания D₁B₁ (рис. 4).

Замечание . Для более глубокого усвоения понятия «Скрещивающиеся прямые» рекомендуем ознакомиться с разделами нашего сайта «Свойства скрещивающихся прямых» и «Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости».