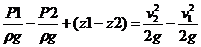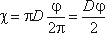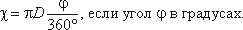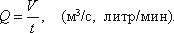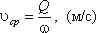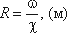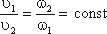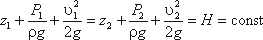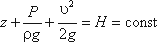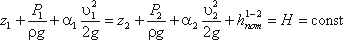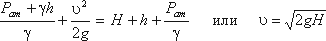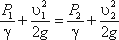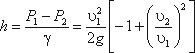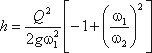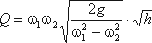Расход и уравнение постоянства расхода

Расход и уравнение постоянства расхода

5-я лекция, 2010 год.

5. КИНЕМАТИКА И ДИНАМИКА ЖИДКОСТИ

5.1. Основные понятия

5.2. Расход. Уравнение расхода

5.3. Уравнение Бернулли для элементарной струйки идеальной жидкости.

Три вида уравнения Бернулли для струйки идеальной жидкости.

5.1. Основные понятия

Кинематика жидкости существенно отличается от кинематики твердого тела. Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют; жидкость состоит из множества частиц движущихся одна относительно другой.

Скорость в данной точке пространства, занятого движущейся жидкостью, является функцией координат этой точки, а иногда и времени.

Задачей кинематики жидкости является определение скорости в любой точке жидкой среды, т. е. нахождение поля скоростей.

Мы сейчас рассмотрим движение идеальной жидкости, то есть жидкости, которая не обладает вязкостью.

В идеальной жидкости, так же как и в неподвижной реальной жидкости, возможен лишь один вид напряжений — нормальные напряжения сжатия, т. е. гидромеханическое давление.

Давление в движущейся идеальной жидкости обладает теми же свойствами, что и в неподвижной жидкости, на внешней поверхности жидкости оно направлено по нормали, а в любой точке внутри жидкости по всем направлениям одинаково.

Течение жидкости может быть установившимся или неустановившимся.

Установившимся называется течение жидкости, при котором давление и скорость являются функциями координат и не зависят от времени.

Давление и скорость могут измениться при перемещении частицы жидкости из одного положения в другое, но в данной неподвижной относительно русла точке давление и скорость при установившемся движении не изменяются во времени.

Последнее положение доказывается подобно тому, как это делалось для неподвижной жидкости (см. п. 1.4): составляются уравнения движения элементарного тетраэдра с учетом сил Д’Аламбера, которые затем вместе с массовыми силами стремятся к нулю при стягивании тетраэдра в точку.

р= f (х, у, z ); v = f ₂(х, у, z ); ,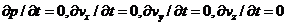

где индексы у скорости означают ее проекции на соответствующие оси, жестко связанные с руслом.

В частном случае установившееся течение может быть равномерным, когда скорость каждой частицы не изменяется с изменением ее координат и поле скоростей остается неизменным вдоль потока .

Примером установившегося течения может служить истечение жидкости из со суда, в котором поддерживается постоянный уровень, или движение жидкости в трубопроводе, создаваемое центробежным насосом с постоянной частотой вращения вала.

Неустановившимся называется течение жидкости, характеристики которого изменяются во времени в точках рассматриваемого пространства.

В общем случае при неустановившемся течении давление и скорость зависят как от координат, так и от времени:

Примерами неустановившегося течения жидкости могут служить быстрое опорожнение сосуда через отверстие в дне или движение во всасывающей или напорной трубе поршневого насоса, поршень которого совершает возвратно-поступательное движение.

Исследование установившихся течений гораздо проще, чем неустановившихся.

При установившемся течении траектории частиц жидкости являются неизменными по времени. При неустановившемся течении траектории различных частиц, проходящих через данную точку пространства, могут иметь разную форму. Поэтому для рассмотрения картины течения, возникающей в каждый данный момент времени, вводится понятие линии тока.

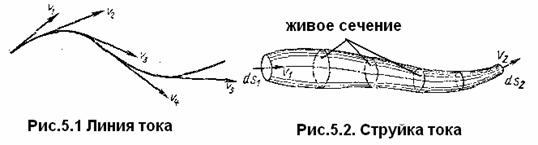
Линией тока называется кривая, в каждой точке которой вектор скорости в данный момент времени направлен по касательной к этой кривой (рис. 5.1).

Очевидно, что в условиях установившегося течения линия тока совпадает с траекторией частицы и не изменяет своей формы с течением времени.

Трубкой тока называется бесконечно малый замкнутый контур, выделенный в данный момент времени в движущейся жидкости, через все точки которого проведены линии тока. Это условная трубчатая поверхность.

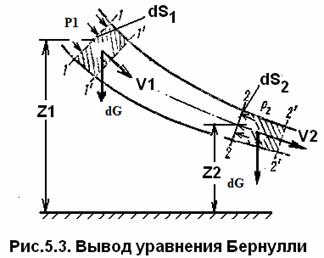
Элементарной струйкой называется часть потока, заключенная внутри трубки тока (рис.5.2).

В любой точке «трубки тока» т.е. на трубчатой поверхности струйки, векторы скорости направлены по касательной, а нормальные к этой поверхности составляющие скорости отсутствуют, следовательно, при установившемся движении ни одна частица жидкости, ни в одной точке трубки тока не может проникнуть внутрь струйки или выйти наружу.

Трубка тока, таким образом, является как бы непроницаемой стенкой, а элементарная струйка представляет собой самостоятельный элементарный поток.

Потоки конечных размеров будем сначала рассматривать, как совокупность элементарных струек, т. е. будем предполагать течение струйным. Из-за различия скоростей соседние струйки будут скользить одна по другой, но не будут перемешиваться одна с другой.

Живым сечением или сечением потока, называется площадь поверхности в пределах потока или струйки, проведенная нормально к линиям тока. Далее будем рассматривать в потоках такие участки, в которых струйки можно считать параллельными и, следовательно, живые сечения плоскими.

Различают напорные и безнапорные течения жидкости. Напорными называют течения в закрытых руслах без свободной поверхности, а безанапорными течения со свободной поверхностью. При напорных течениях давление вдоль потока обычно переменное, при безнапорном на свободной поверхности постоянное и чаще всего атмосферное. Примерами напорного течения могут служить течения в трубопроводах с повышенным (или пониженным) давлением, в гидромашинах или других гидроагрегатах. Безнапорными являются течения в реках, открытых каналах и лотках.

5.2. Расход. Уравнение расхода

Расходом называется количество жидкости, протекающее через живое сечение потока в единицу времени. Это количество можно измерить в единицах объема, в весовых единицах, в единицах массы в связи, с чем различают объемный Q , весовой Q_G и м ассовый расходы Q_m .

Для элементарной струйки, имеющей бесконечно малые площади сечений, можно считать истинную скорость одинаковой во всех точках каждого сечения. Следовательно, для этой струйки расходы равны.

объемный, (м 3 /с) dQ = v * dS , (5.136)

весовой, (Н/с) d Q_G = ρg * dQ , (5.2)

массовый, (кг/с) dQ_m = ρv * dS , (5.3)

где dS – площадь сечения струйки.

Для потока конечных размеров в общем случае скорость имеет различное значение в разных точках сечения, поэтому расход надо определять, как сумму элементарных расходов струек в данном сечении.

Q = 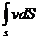. (5.4)

Обычно в рассмотрение вводят среднюю по сечению скорость v _ср = Q / S , откуда средний расход для струйки или потока равен

Условие неразрывности потока основывается на следующих свойствах, законе и предпосылках.

а) трубка тока имеет свойство непроницаемости для внешних, обтекающих ее потоков;

б) закон сохранения вещества;

в) предположение о сплошности (неразрывности) среды для установившегося течения несжимаемой жидкости.

На основании этих предпосылок и свойств можно утверждать, что объемный расход во всех сечениях элементарной струйки (см. рис.5.2) один и тот же

dQ = v ₁ * dS ₁ = v ₂ * dS ₂ → const (вдоль струйки). (5.6)
Это уравнение называется уравнением объемного расхода для элементарной струйки.

Аналогичное уравнение можно составить и для потока конечных размеров, ограниченного непроницаемыми стенками, только вместо истинных скоростей следует ввести средние скорости. В результате

Из последнего уравнения следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональны площадям сечений:

У равнение расхода (5.6‘) является следствием общего закона сохранения вещества для частных условий, в частности? для условий сплошности (неразрывности) течения.

5.3. Уравнение Бернулли для элементарной струйки

Рассмотрим установившееся течение идеальной жидкости находящейся под действием одной массовой силы — силы тяжести, и выведем для этого случая основное уравнение, связывающее между собой давление в жидкости и скорость ее движения.

Возьмем одну из элементарных струек, составляющих поток, выделим сечениями 1 и 2 участок этой струйки произвольной длины (рис.5.3). Пусть площадь первого сечения равна dS ₁ , скорость в нем V ₁ , давление P ₁ , а высота от произвольной плоскости сравнения Z ₁ . Во втором сечении dS ₂ , V ₂ , P ₂ и Z ₂ .

За бесконечно малый отрезок времени dt выделенный участок струйки переместится в положение 1’ – 2’ .

Применим к массе жидкости в объеме участка струйки теорему о кинетической энергии: работа сил, приложенных к телу, равна приращению кинетической энергии этого тела.

На жидкость действуют силы тяжести и силы давления, нормально к поверхности сечения рассматриваемого участка струйки.

Подсчитаем работу сил давления, сил тяжести и изменение кинетической энергии участка струйки за время dt . Эта теорема выглядит следующим образом.

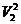
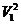
( m )/2 — ( m )/2 = G * h = G * (Z₁-Z₂)

Работа силы давления в первом сечении положительна, так как направление силы совпадает с направлением перемещения, и выражается как произведение силы p ₁* dS на путь V ₁ dt :

Работа силы давления во втором сечении имеет знак минус, так как направление силы прямо противоположно направлению перемещения, и определяется выражением

Силы давления, действующие по боковой поверхности отрезка струйки, работы не производят, так как они нормальны к этой поверхности и к перемещениям.

Работа сил давления равна

Работа силы тяжести равна изменению потенциальной энергии положения участка струйки, поэтому надо из потенциальной энергии жидкости в объеме 1 — 2 вычесть потенциальную энергию жидкости в объеме 1’- 2’ . При этом энергия промежуточного объема 1’- 2 сократится, и останется лишь разность энергии элементов 1- 1’ , 2- 2’ .

ПО уравнению расходов (закон сплошности среды) ( 5.6’ ) объемы и силы тяжести заштрихованных элементов 1 -1’ и 2 — 2’ равны между собой:

Тогда работа силы тяжести выразится как произведение разности высот на силу тяжести dG :

Чтобы подсчитать приращение кинетической энергии рассматриваемого участка струйки за время dt , необходимо из кинетической энергии объема 1’- 2’ вычесть кинетическую энергию объема 1 — 2. При вычитании кинетическая энергия промежуточного объема 1’ — 2 сократится, и останется лишь разность кинетических энергий элементов 2 — 2’ и 1 — 1’ , масса каждого из которых равна dG / g .

Таким образом, приращение кинетической энергии на участке струйки равно

Сложив работу сил давления (см. уравнение 5.7) с работой силы тяжести (5.9) и приравняв эту сумму приращению кинетической энергии (5.10), получим исходное уравнение для трех видов уравнения Бернулли.

Разделим это уравнение на dG (изменение силы тяжести элементарной струйки за время dt ) (см. формулу (5.8) , и произведя сокращения на

Сгруппируем члены, относящиеся к первому сечению, в левой части уравнения, а члены, относящиеся ко второму сечению, в правой:

( 5 . 12 )

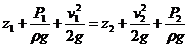
где z — геометрическая высота, или геометрический напор;

Р/ρ g – пьезометрическая высота или пьезометрический напор;

v 2 /2 g — скоростная высота или скоростной напор.

Полученное уравнение называется уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости. Оно было выведено Даниилом Бернулли в 1738 г .

Это уравнение является первой формой уравнения Бернулли, оно

( 5 . 13 )

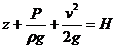
называется полным напором и имеет размерность длины.

Данное уравнение получено путем деления исходного уравнения (5.11), выражающего теорему об изменении кинетической энергии элементарной струйки, на ее изменении ее силы тяжести за время dt .

Уравнение Бернулли (5.13) записано для двух произвольно взятых сечении струйки и выражает равенство полных напоров Н в этих сечениях. Так как сечения взяты произвольно, следовательно, и для любого другого сечения этой же струйки полный напор будет иметь то же значение

(вдоль струйки)

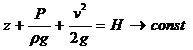
Для идеальной движущейся жидкости вдоль струйки тока сумма трех напоров: геометрического, пьезометрического и скоростного есть величина постоянная.

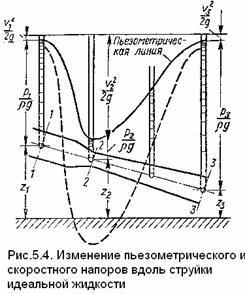
На рис. 5.4 показано изменение всех напоров вдоль струйки.

Линия изменения уровней жидкости в пьезометрах называется пьезометрической линией.

Из уравнения Бернулли и уравнения расхода следует, что если площадь поперечного сечения струйки уменьшается, т. е. струйка сужается, то скорость течения жидкости увеличивается, а давление уменьшается, и наоборот, если струйка расширяется, то скорость уменьшается, а давление возрастает.

На рис. 5.4 площадь поперечного сечения струйки от сечения 1 — 1 к сечению 2 — 2 уменьшается в 4 раза, скоростной напор увеличивается в 16 раз, а сечение 3 — 3 имеет ту же площадь, что и сечение 1-1.

Штриховой линией показано положение пьезометрической линия при тех же сечениях и при увеличении расхода в 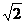раз, вследствие чего скоростные высоты увеличиваются в 2 раза, а в узкой части струйки давление становятся меньше атмосферного.

Уравнение Бернулли можно записать в двух других формах. Разделив уравнение (5.11) на расход dQ = dS ₁* v ₁ dt = dS ₂* v ₂ dt , учитывая, что dG = ρ *g*dQ, а dQ = dG / ρ g, получим

, (5.15)

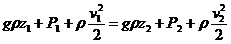
где все величины выражены в виде давлений.

В этой форме члены уравнения Бернулли имеют размерность давления и имеют следующие называния: ρ zg — весовое давление; р — гидромеханическое давление; ρ v 2 /2 — динамическое давление.

Разделив уравнение (5.11) на массу dm элементарного объема, равную ( ρ * v _1* dS ₁) * dt = ( ρ * v _2* dS ₂) * dt и преобразуем это уравнение подобно предыдущему. Тогда вместо выражения (5.15) будем иметь

(5.16)

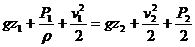
Введем понятие удельной энергии жидкости, в качестве которой рассмотрим отношение энергии к массе или объему.

Нетрудно показать, что члены уравнения (5.16) представляют собой различные формами удельной механической энергии, а именно:

gz — удельная потенциальная энергия (ее еще называют энергией положения), так как частица жидкости массой Δ m , находясь на высоте z , обладает энергией равной Δ mgz , а на единицу массы приходится энергия g Δ mz /Δ m = gz ;

р/ρ — удельная энергия давления (движущейся) жидкости, так как частица массой Δ m при давлении р обладает способностью подняться на высоту h = р/ρ g и приобрести, таким образом, энергию положения Δ mg р/(ρ g ) = р/ρ (после деления на Δ m получаем р/ρ);

сумма gz + р/ρ – удельная потенциальная энергия жидкости;

v 2 /2 — удельная кинетическая энергия жидкости, так как для той же частицы Δ m кинетическая энергия отнесенная к ее массе Δ m v 2 /2 : Δ m = v 2 /2;

Hg = zg + p /ρ+ v 2 /2 – полная удельная механическая энергия движущейся жидкости.

Таким образом, энергетический смысл уравнения Бернулли для элементарной струйки идеальной жидкости заключается в постоянстве вдоль струйки полной удельной энергии жидкости.

Механическая энергия жидкости может иметь три формы: потенциальная энергия, энергия давленияи и кинетическая энергия.

Первая и третья формы механической энергии известны из механики, они свойственны твердым и жидким телам.

Энергия давления является специфической для движущихся жидкостей. В процессе движения идеальной жидкости одна форма энергии может превращаться в другую, однако полная удельная энергия идеальной жидкости при этом как следует из уравнения Бернулли, остается без изменений.

Энергию давления легко преобразовать в механическую работу. Простейшим устройством, с помощью которого осуществляют такое преобразование, является цилиндр с поршнем (рис. 5.5). Покажем, что при этом преобразовании каждая единица массы жидкости совершает работу, численно равную р/ρ.

Пусть площадь поршня равна s , его ход L , избыточное давление жидкости в левой полости цилиндра необходимое для преодоления силы F равно Р = F / S , избыточное давление по другую сторону поршня равно нулю. Преодолевая силу F при перемещении поршня из левого положения, давление совершает работу А = Р SL . Расход жидкости, которую необходимо подвести к цилиндру для совершения этой работы за время t , равен объему цилиндра, т. е. Q t = W = SL .Удельная работа, приходящаяся на 1 кг массы,

Лекция по электроснабжение предприятий

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Тема: Основные уравнения движения

1. Уравнение неразрывности потока. Уравнение постоянства расхода

3. Уравнение Бернулли и его практическое применение

4. Дифференциальные уравнения движения идеальной и вязкой жидкости

5. Основные характеристики турбулентного движения

6. Подобие и моделирование гидромеханических процессов

1. Уравнение неразрывности потока. Уравнение постоянства расхода

Уравнение неразрывности элементарной струйки: скорости и площади поперечных сечений струек в различных живых сечениях могут меняться, однако произведение скорости отдельных частиц струйки на площади их поперечного сечения остаются постоянными

. (4.1)

Рассмотрим установившееся движение в русле переменного сечения (рисунок 4.1). Выберем два произвольных сечения I — I и II — II , нормальных к оси потока, и рассмотрим участок потока, заключённый между сечениями.

Рисунок 4.1 – Схема к уравнениям постоянства расхода и неразрывности потока

Так как жидкость несжимаема, а стенки русла жёсткие, то на основе второго свойства элементарной струйки можно записать уравнение постоянства расхода

. (4.2)

Уравнение постоянства расхода гласит: в любом сечении потока при установившемся движении несжимаемой жидкости её расход одинаков.

Так как , то получаем уравнение неразрывности потока

. (4.3)

Уравнение неразрывности потока гласит: при установившемся движении несжимаемой жидкости произведение средней скорости потока на площадь живого сечения является постоянной величиной.

Через сечения потока жидкости в единицу времени проходит одно и то же количество жидкости

. (4.4)

Из уравнения 4.4 следует, что средние скорости потока обратно пропорциональны площадям соответствующих сечений

или . (4.5)

Дифференциальное уравнение неразрывности имеет вид

, (4.6)

где — расход элементарной струйки;

— бесконечно малая площадь поперечного сечения струйки;

— скорость в поперечном сечении элементарной струйки.

Энергия – это физическая величина, которая показывает, какую работу, может совершить тело.

Известно, что механическая энергия любого тела характеризуется двумя величинами:

а) кинетической энергией (это энергия движения, зависящая от массы тела и скорости его движения)

, (4.7)

где — масса тела или частицы;

— скорость движения тела или частицы;

б) потенциальной энергией (это энергия, которая определяется взаимным расположением тел или частей одного тела).

Потенциальная энергия тела или частицы, поднятого на высоту

. (4.8)

Если масса жидкого тела занимает объём и находится под давлением , то это тело ещё обладает потенциальной энергией давления

. (4.9)

Полная механическая энергия элементарной струйки (частицы) определяется по формуле

, (4.10)

где — масса элементарной струйки (частицы);

— скорость элементарной струйки (частицы).

Удельная энергия струйки – это энергия, отнесённая к единице веса.

, (4.11)

где — удельная кинетическая энергия струйки;

— удельная потенциальная энергия струйки.

Так как поток жидкости представляет собой совокупность множества элементарных струек, и, принимая движение потока установившимся или плавно изменяющимся, можно определить удельную энергию потока жидкости конечных размеров.

Рассмотрим поток жидкости в виде наклонной трубы с плавно изменяющимся сечением (рисунок 4.2).

Рисунок 4.2 – Схема к выводу уравнения энергии потока жидкости

Внутри потока выделим некоторую точку . Обозначим расстояние от этой точки до произвольно выбранной плоскости (плоскость сравнения) — , давление жидкости в центре тяжести сечения — , среднюю скорость движения жидкости в выбранном сечении — .

Полная энергия потока будет равна

,

где — удельная кинетическая энергия потока;

— удельная потенциальная энергия.

Удельная кинетическая энергия определяется

, (4.12)

где — число элементарных струек;

— скорости элементарных струек;

— средняя скорость потока;

— коэффициент, учитывающий неравномерность распределения скорости по сечению.

Удельная потенциальная энергия согласно гидростатическому закону определяется

, (4.13)

то есть для всех точек данного объёма покоящейся жидкости удельная потенциальная энергия относительно выбранной плоскости сравнения постоянна.

Тогда полная удельная энергия потока в выбранном сечении примет вид

. (4.14)

Так как распределение скоростей в потоке неизвестно, то в механике жидкостей и газов эти скорости принимаются одинаковыми, а при определении кинетической энергии потока вводится поправочный коэффициент .

Поправочный коэффициент — коэффициент кинетической энергии (коэффициент Кориолиса) учитывает изменение кинетической энергии из-за неравномерного распределения скоростей в живом сечении потока.

— для равномерных турбулентных потоков.

— для равномерных ламинарных потоков.

3. Уравнение Бернулли и его практическое применение

В потоке жидкости, движущейся в трубке с плавно изменяющимся сечением (рисунок 4.3), выберем два произвольных сечения I — I и II — II . Обозначим и — давления в центрах тяжести сечений и , и — средние скорости, и — вертикальные координаты оси потока в выбранных сечениях.

Рисунок 4.3 – Схема к выводу уравнения Бернулли

Тогда величины полной удельной энергии потока в сечениях I и II соответственно могут быть записаны

. (4.15)

. (4.16)

При движении реальной жидкости часть энергии затрачивается на преодоление силы трения (сопротивления) на пути от первого сечения до второго. Эта энергия обращается в тепло и рассеивается.

Величину потерь обозначим .

Тогда баланс энергии в сечениях I и II (уравнение Бернулли для реального потока жидкости) можно записать

, (4.17)

, (4.18)

где — высота скоростного потока;

— пьезометрическая высота, отсчитываемая в каждом сечении по пьезометру;

— геометрическая высота;

— потерянный напор, равный части энергии, превращённой в тепло.

Уравнение Бернулли устанавливает математическую связь между основными элементами движения жидкости, то есть средней скоростью и гидродинамическим давлением. Оно показывает, что за счёт преобразования одного вида энергии в другой наблюдается при возрастании скорости и уменьшение давления и, наоборот, при уменьшении скорости – возрастание давления.

Физический (энергетический) смысл уравнения Бернулли состоит в том, что при установившемся движении жидкости сумма трёх удельных энергий (положения, давления и кинетической) остаётся неизменной.

Гидродинамический напор – это сумма скоростного напора, геометрической и пьезометрической высот

. (4.19)

На основании уравнения Бернулли сконструирован ряд приборов (водомер Вентури, водоструйный насос, эжектор и др.).

Рассмотрим применение уравнения Бернулли на примере водомерного устройства в трубах – водомера Вентури (рисунок 4.4), который представляет собой вставку в основную трубу диаметром трубы меньшего диаметра . Труба меньшего диаметра соединена с основной трубой коническими переходами.

В основной трубе (сечение I — I ) и в суженном сечении (сечение II — II ) присоединены пьезометры, по показаниям которых определяется расход жидкости в трубе.

Рисунок 4.4 – Схема водомера Вентури

Выведем общую формулу водомера для определения расхода жидкости.

Примем для заданных условий ; и ( из-за малости расстояния между сечениями). Составим уравнение Бернулли для точек, расположенных в центре тяжести сечений при плоскости сравнения О-О, проходящей по оси трубы

или .

Из рисунка 4.4 видно, что

→ .

В последнем уравнении неизвестны величины и . Применяя уравнение неразрывности, можно записать , откуда .

.

Скорость течения в основной трубе (сечение I — I ) равна

.

Так как , то .

Обозначим постоянную величину для данного водомера через :

, тогда ,

где — коэффициент, учитывающий потери напора в водомере, принимается равным 0,96…0,98.

Таким образом, зная диаметры водомера в расширенном и суженном сечениях, по разности давлений , измеряемой пьезометрами, можно легко определить расход воды.

В водоструйном насосе (рисунок 4.5) вода из бака 1 поступает в трубу, имеющую сужение. В узком сечении трубы скорость возрастает. При этом в соответствии с уравнением Бернулли давление здесь падает ниже атмосферного, поэтому происходит подсасывание жидкости по трубке, опущенной в бак 2. При больших скоростях движения жидкость будет подсасываться из бака 2 непрерывно.

Рисунок 7.5 – Схема водоструйного насоса

Скорость течения движущейся жидкости можно определить трубкой Пито . Этот прибор (рисунок 4.6) представляет собой стеклянную трубку, открытую с двух концов. При этом изогнутый под прямым углом конец трубки располагается в жидкости так, чтобы ось нижнего колена совпадала с линией тока.

Рисунок 4.6 – Схема прибора с трубкой Пито

В трубке Пито создаётся дополнительное давление от воздействия скорости движущейся жидкости (скоростной напор)

; ;

практически ,

где — коэффициент, зависящий от конструкции трубки и определяемый путём тарировки.

4. Дифференциальные уравнения движения идеальной и вязкой жидкости

Рассматриваемые уравнения представляют собой математическое выражение закона сохранения количества движения применительно к жидкому элементу: скорость изменения вектора количества движения равна сумме всех массовых и поверхностных сил, действующих на рассматриваемый жидкий элемент.

В качестве такого элемента используем жидкий прямоугольный параллелепипед с рёбрами (рисунок 4.7), на который действуют суммарный вектор поверхностных сил и вектор массовых сил, причём оба эти вектора отнесены к единице объёма.

Рисунок 4.7 – Схема к выводу дифференциальных уравнений движения идеальной жидкости

В данном случае рассматривается движение идеальной жидкости. Единственной поверхностной силой является сила, обусловленная гидродинамическим давлением .

На грани, перпендикулярные оси , будут действовать следующие силы: на левую грань — ; на правую грань — .

Учитывая принятое направление осей, получаем для поверхностей силы, отнесённой к единице объёма, действующей в направлении оси , .

Аналогично ; .

Уравнения движения идеальной жидкости (уравнения Эйлера) имеют вид

;

; (4.20)

.

Для плоского установившегося движения уравнения Эйлера имеют вид

;

. (4.21)

При одномерном течении (когда параметры потока и скорость зависят только от одной координаты) уравнение Эйлера имеет вид

. (4.22)

Уравнения движения, записанные с учётом сил вязкости, существенно усложняются. В отличие от идеальной жидкости поверхностные силы в общем случае направлены не нормально, а под произвольным углом к выделенной площадке.

Для вязкой жидкости уравнение движения (уравнение Навье-Стокса) имеет вид

;

; (4.23)

;

.

5. Основные характеристики турбулентного движения

Для турбулентного режима характерны перемешивание жидкости , пульсации скоростей и давлений в процессе движения. Поэтому механизм турбулентного потока очень сложен.

Движение жидкости становится турбулентным при достижении числом Рейнольдса критического значения. Тогда от стенок трубы отрываются отдельные жидкие массы, попадающие внутрь потока и своим перемещением нарушающие существовавшее до того упорядоченное (подслойное) движение.

В результате возникает диффузия образовавшихся у стенки вихрей, сопровождающаяся гашением заключённой в вихрях кинетической энергии турбулентности. При этом механическая энергия потока переходит частично в тепловую.

Из-за интенсивного вихреобразования частицы жидкости при турбулентном движении описывают весьма сложные траектории, а местные скорости не сохраняются постоянными даже в том случае, когда расход потока постоянен во времени.

Установившегося движения в турбулентном потоке не существует. В каждой точке потока скорость непрерывно меняется по величине и направлению.

Мгновенная местная скорость – это скорость в точке турбулентного потока.

Разложим мгновенную скорость на три взаимно перпендикулярных направления. Получим продольную составляющую , направленную по нормали к живому сечению, и две поперечные составляющие и , лежащие в плоскости живого сечения потока (рисунок 4.8).

Рисунок 4.8 – Составляющие пульсационных скоростей в турбулентном потоке

Как продольные, так и поперечные составляющие мгновенной скорости всё время меняются.

Пульсация скорости – это изменение во времени проекции мгновенной местной скорости на какое-либо направление. Пульсация скорости наблюдается с помощью чувствительных приборов. На рисунке 4.9 показан график пульсации.

Рисунок 4.9 – Пульсация мгновенной местной скорости в турбулентном потоке

Изменения скорости кажутся беспорядочными, но осреднённое за достаточно длинный промежуток времени значение скорости сохраняется постоянным. Это значит, что скорость непрерывно пульсирует около некоторого среднего (осреднённого во времени) значения .

Пульсировать – это подвергаться знакопеременным изменениям относительно какой-то средней величины.

Графически осреднённая скорость выражается высотой прямоугольника, равновеликого площади, заключённой между пульсационной кривой, осью абсцисс и двумя ординатами, соответствующими начальному и конечному моменту наблюдения. Для определения осреднённой скорости важно иметь достаточный период наблюдений, так как закономерной периодичности пульсационных кривых не обнаружено.

Осреднённая скорость – средняя скорость движения в данной точке, определяемая за достаточно продолжительный промежуток времени.

Пульсационная составляющая скорости (пульсационная добавка) – это разность между истинным и осреднённым значением местной скорости. Пульсационные добавки обозначаются теми же буквами, что и сами скорости, но со штрихом.

Пульсационная составляющая в продольном направлении имеет вид

. (4.24)

В турбулентном потоке вместо поля мгновенных скоростей можно рассматривать поле осреднённых скоростей. Только имея в виду осреднённые скорости, можно говорить об установившемся турбулентном движении.

Уравнение осреднённого движения турбулентного потока (уравнение Рейнольдса) имеет вид

, (4.25)

где — период наблюдений.

Также можно осреднить и другие компоненты скорости — и , а также любую другую быстро меняющуюся во времени величину, например произведение скоростей и , давление и другие.

Обычно рассматриваются не истинная, а только осреднённая скорость, а также поле осреднённых скоростей.

Вопросы для самопроверки

1 Как выглядит уравнение неразрывности элементарной струйки?

2 Какой вид имеет уравнение неразрывности потока и о чём оно гласит?

3 Что такое энергия?

4 Какими величинами характеризуется механическая энергия любого тела?

5 В чём заключается различие между кинетической и потенциальной энергиями?

6 Как определяется полная механическая энергия элементарной струйки?

7 Как определить удельную энергию струйки?

8 Чему равна полная энергия потока?

9 Как определить удельную кинетическую и удельную потенциальную энергии?

10 Чему равна полная удельная энергия потока?

11 Что учитывает коэффициент Кориолиса?

12 Какой вид имеет уравнение Бернулли для реального потока жидкости?

13 В чём заключается энергетический смысл уравнения Бернулли?

14 Что такое гидродинамический напор?

15 Как применяется уравнение Бернулли для водомера Вентури?

16 Практическое применение уравнения Бернулли на примере водоструйного насоса.

17 Что представляет собой трубка Пито?

18 Какой вид имеет дифференциальное уравнение движения идеальной жидкости?

19 как запишется уравнение Эйлера для плоского установившегося движения и одномерного течения?

20 какой вид имеет дифференциальное уравнение движения для вязкой жидкости?

21 Каковы основные характеристики турбулентного движения?

22 Дайте определение понятию мгновенной местной скорости.

23 Что такое пульсация скорости?

24 Что называется осреднённой скоростью и пульсационной составляющей скорости?

Расход и уравнение постоянства расхода

Гидродинамика — раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие с неподвижными и подвижными поверхностями.

Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.

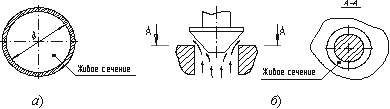
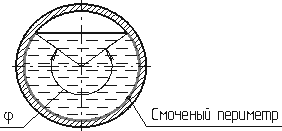
Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную к направлению течения. Например, живое сечение трубы — круг (рис.3.1, б); живое сечение клапана — кольцо с изменяющимся внутренним диаметром (рис.3.1, б).

Смоченный периметр χ («хи») — часть периметра живого сечения, ограниченное твердыми стенками (рис.3.2, выделен утолщенной линией).

Для круглой трубы

если угол в радианах, или

Расход потока Q — объем жидкости V, протекающей за единицу времени t через живое сечение ω.

Средняя скорость потока υ — скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

Гидравлический радиус потока R — отношение живого сечения к смоченному периметру

Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным

Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Трубка тока — трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока называется элементарной струйкой.

Течение жидкости может быть напорным и безнапорным. Напорное течение наблюдается в закрытых руслах без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением). Безнапорное — течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые каналы, лотки и т.п.). В данном курсе будет рассматриваться только напорное течение.

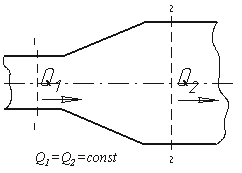
Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q₁=Q₂= const, откуда

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:

Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.

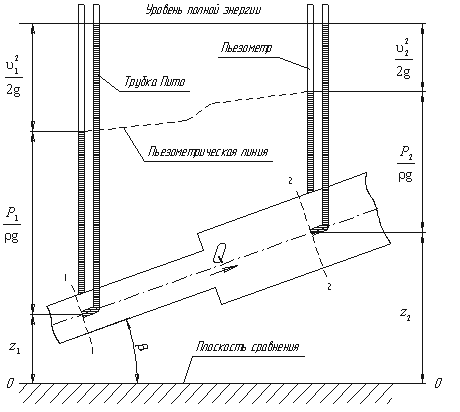
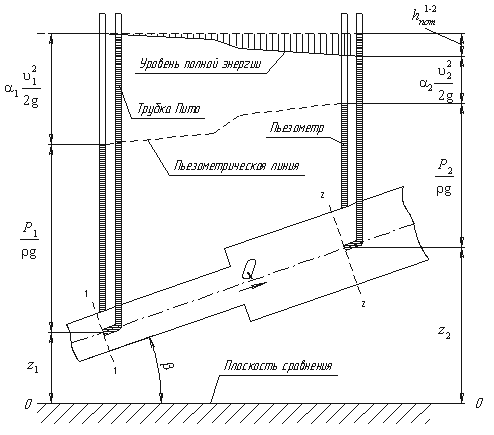
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).

Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.

Для измерения давления жидкости применяют пьезометры — тонкостенные стеклянные трубки, в которых жидкость поднимается на высоту 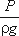. В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.

Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.

Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).

Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.

Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.

Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:

Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.

С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:

z1 и z2 — удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;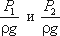
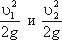
— удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
— удельные кинетические энергии в тех же сечениях.

Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.

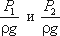
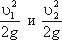
Уравнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Глядя на рис.3.5, можно заметить, что z1 и z2 — геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения; — пьезометрические высоты; — скоростные высоты в указанных сечениях.

В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).

Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента α₁ и α₂, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).

Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

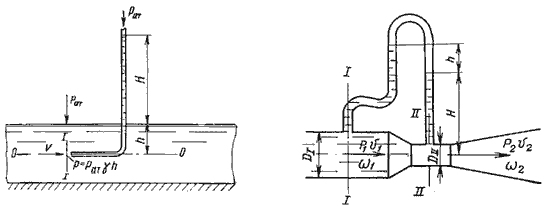
Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим

где Н — столб жидкости в трубке Пито.

Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:

Выражение, стоящее перед 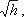, является постоянной величиной, носящей название постоянной водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.