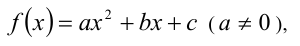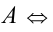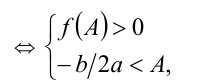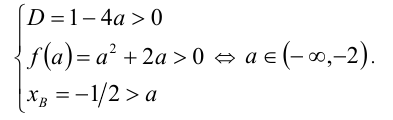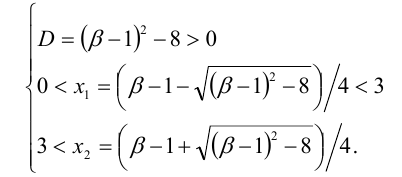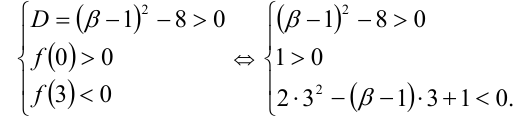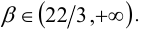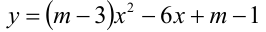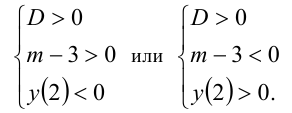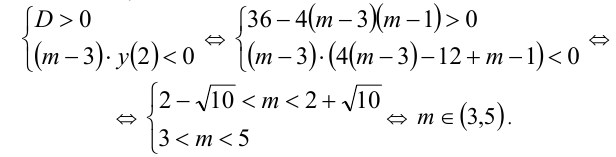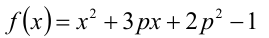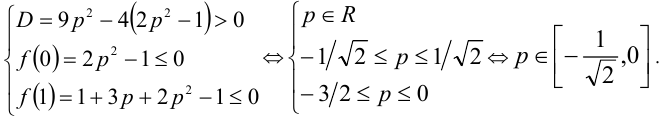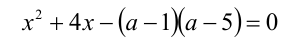Расположение корней квадратного уравнения относительно заданных точек

Расположение корней квадратного уравнения относительно заданных точек

Разделы: Математика

“Будущий математик, как и всякий человек учится при помощи практики и подражания… .Ему следует решать задачи, выбирая те, которые соответствуют его интересам, размышлять над их решением и изобретать новые задачи.”
Дьердь Пойа

• Повторить свойства графика квадратичной функции у = aх² + bх + с, а ≠ 0;
• Повторить теорему Виета для корней квадратного уравнения ах² + bх + с = 0;
• Рассмотреть алгоритм решения квадратного уравнения с параметром в котором поставлено условие для корней х₁ и х₂;
• Применять алгоритм для решения уравнений с параметром с поставленными условиями;
• Воспитывать чувство ответственности перед товарищами и умение работать в группах
• Развивать логическое мышление.

1. Организационный момент.
2. Актуализация знаний учащихся:

• Повторение свойств графика квадратичной функции
• Повторение Теоремы Виета.

3. Изучение нового материала. Работа в группах:
Исследовательская работа. Отчет о проделанной работе.
4. Закрепление изученного материала.
5. Домашнее задание.
6. Итог занятия.

Оборудование: Мультимедийное оборудование, презентация, (Приложение 1)

1. Организационный момент

Рассмотреть рисунки. Что общего на всех эти картинах? Что просматривается на этих картинах? (Слайд 3, 4 ,5)

2. Актуализация знаний учащихся.

Парабола…
Что такое парабола?
Как может располагаться парабола в системе координат? Отчего это зависит? (Слайд 6, 7)

3. Изучение нового материала.

Нас сегодня будет интересовать случай, когда парабола пересекает ось абсцисс в двух точках, т.е. квадратное уравнение ах²+bх+с=0 имеет два корня.
Возьмем на оси абсцисс произвольную точку М. Давайте рассмотрим все случаи расположения точки М и корней квадратного уравнения х₁ и х2.

Исследовательская работа в группах: (Слайд 8, 9, 10, 11)

А вы, ребята, должны провести исследовательскую работу.

(Работа в группах.)

Задания даны на ваших инструкционных картах вместе с графиком.
Работаем 6–8 минут. А затем готовим выступление по своей работе.
Выводы записываем в заранее заготовленную таблицу на доске (или через компьютерную презентацию).

Вместе вырабатываем (план) Алгоритм решения квадратного уравнения с параметром относительно заданных точек.

Алгоритм решения. (Cлайд 12)

• Постановка проблемы.
• Путь решения.
• Составить математическую модель. (Ввести функцию.)
• Найти решение.
• Записать ответ.

5. Закрепление изученного материала. (Слайд 13)

При каких значениях а оба корня уравнения х² – ах + 2 = 0 лежат в промежутке (0; 3)

1. Проблема поставлена условием задачи.
2. Воспользуемся первым способом решения:

3. Составим модель решения квадратного уравнения с параметром.

D = b ² – 4 ac
a ² – 4•1 •2 > 0

лежат в промежутке (-1; 5)Ответ:

Самостоятельно в тетрадях:

При каких значениях а оба корня лежат в промежутке (-1; 2)

6. Домашнее задание.

1) х 2 – ах + 2 = 0 лежат в промежутке (1; 3) Ответ: [2√2; 3)

2) 4х 2 – 2х + а = 0 лежат в промежутке (-1; 1) Ответ: (-2; 0,25]

7. Итог занятия. (Слайд 14)

“Считать несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию”
Ян Амос Каминский

– Что нового узнали?
– Чему научились?

Расположение корней квадратного трёхчлена относительно одной-двух заданных точек («метод парабол»)

Расположение корней квадратного трёхчлена относительно одной-двух заданных точек («метод парабол»)

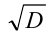
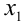
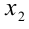
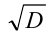
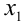
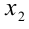
Многие задачи с параметрами сводятся к исследованию расположения корней квадратного трёхчлена относительно заданной точки или заданного промежутка (отрезка, интервала, луча). При этом если дискриминант D квадратного трёхчлена есть полный квадрат некоторого выражения (т.е. извлекается ), то в подавляющем большинстве случаев проще найти корни ,квадратного трёхчлена и подчинить их условиям задачи. Если же — не извлекается (остаётся радикал), то в принципе также можно найти корни , квадратного трёхчлена и подчинить их условиям задачи, но при этом придётся решать непростые иррациональные неравенства, которые приводят к большим и утомительным вычислениям. В этом случае более удобным оказывается следующий подход (иногда называемый методом парабол), использующий графическую интерпретацию расположения корней квадратного трёхчлена, вершины его графика по отношению к заданной точке (точкам).

Итак, пусть задана квадратичная функция

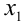
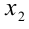
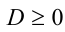
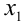
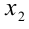
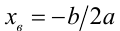
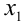
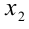
график которой имеет точки, пересечения с осью абсцисс (т.е. ). Пусть, для определённости, ветви параболы направлены вверх. Выпишем, например, условия, необходимые и достаточные для того, чтобы оба корня , были меньше заданного действительного числа А . Очевидно, что в этом случае вершина параболы должна располагаться левее точки x = А , и значение данной квадратичной функции в точке А должно быть положительно. Таким образом, оба корня , меньше заданного числа

т.е. данная система условий однозначно задаёт рассматриваемую ситуацию в расположении корней по отношению к А .

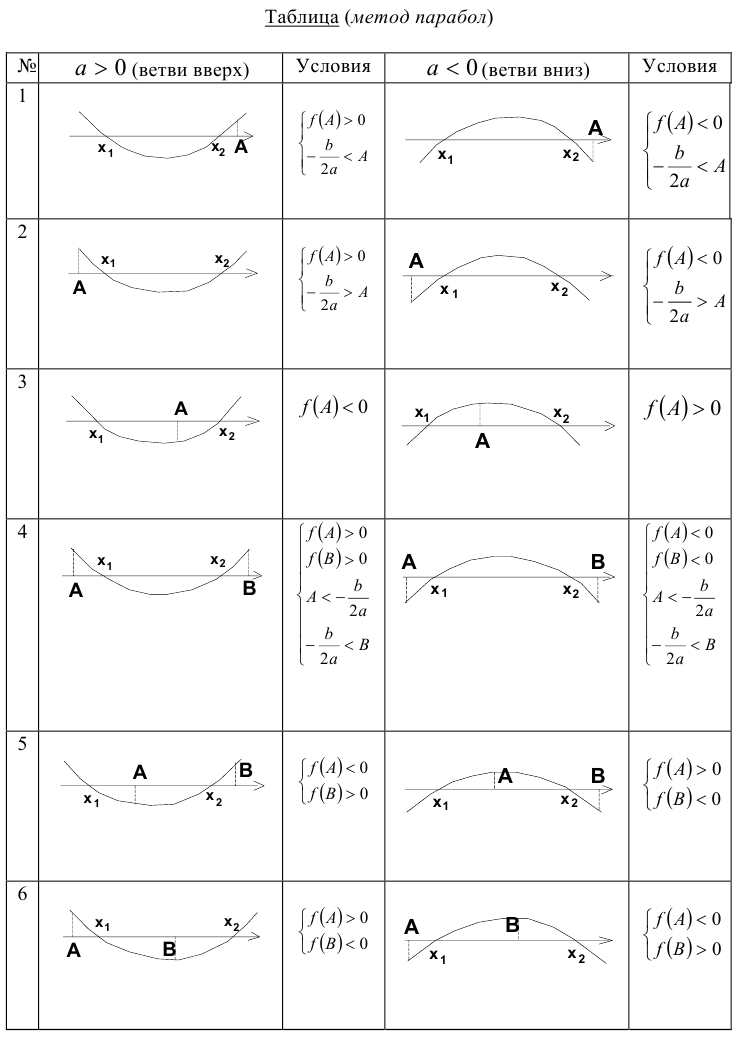
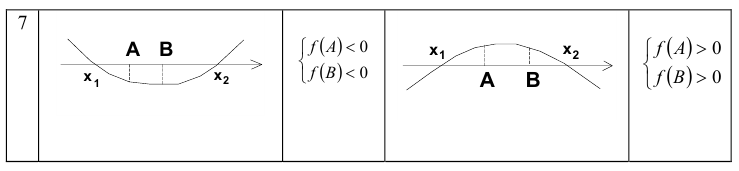
Понятно, что по отношению к одному заданному числу А возможны всего три ситуации: оба корня меньше А , оба корня больше А , корни расположены по разные стороны от А . Если же заданы два действительных числа А и В , то по отношению к ним возможны уже четыре ситуации расположения корней квадратного трёхчлена. Оформим полученный специальный метод в виде следующей таблицы.

Замечание. При использовании данного метода внимательно читайте условие задачи. В зависимости от постановки задачи знак в неравенствах, приведённых в таблице, может быть как строгим, так и нестрогим. Неверно поставленный знак может привести к потере или, наоборот, к приобретению посторонних корней.

Пример №164.

Найти все значения параметра а , при которых корни уравнения 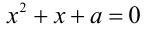действительные, различные и оба больше а .

Решение:

В этой задаче реализуется случай 2 из таблицы выше. Обозначим 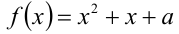. В соответствии с методом, решение задачи сводится к системе

Пример №165.

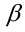
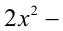
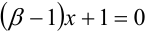
При каких значениях оба корня уравнения положительны и расположены по разные стороны от числа 3?

Решение:

Выпишем два способа решения задачи — стандартный и специальный, изложенный выше, и сравним их по эффективности.

Стандартный способ решения сводится к решению системы

Специальный метод состоит в решении следующей системы (см. случай 6 в таблице; через f(x) обозначен многочлен в левой части уравнения):

Условие положительности дискриминанта учтено в обоих способах решения. Но если при стандартном способе надо решать два иррациональных неравенства (одно из которых двойное), то при выборе второго способа вместо этого имеем два линейных неравенства (одно из которых тривиально). Безусловно, при решении данной задачи следует предпочесть второй вариант решения.

Ответ:

Пример №166.

Найти все значения параметра m , при которых один из корней квадратного трёхчлена

меньше, а другой больше двух.

Решение:

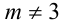
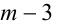
По условию . В зависимости от знака старшего коэффициента возможны два случая (см. пункт 3 в таблице):

Заметим, что эти случаи легко объединить в один:

Пример №167.

Найти наибольшее значение параметра p , при котором функция

принимает отрицательные значения в интервале (0,1).

Решение:

По условию задачи составляем систему (см. пункт 7 в таблице):

Ответ: наибольшее значение p равно 0.

Заметим, что необходимость использования приведённого метода при решении задач, связанных с корнями квадратного уравнения, возникает не всегда. Например, в следующей задаче вполне можно обойтись стандартным методом.

Пример №168.

При каких значениях параметра а больший корень уравнения

принадлежит промежутку [0,1) ?

Решение:

В данной задаче дискриминант является полным квадратом и, следовательно, корни имеют рациональные выражения: 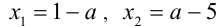. Согласно условию задачи, возможны два случая.

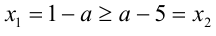
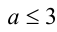
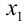
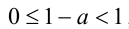
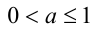
1) Если , т.е. , то большим является корень , и условие задачи приводит к неравенству , откуда .

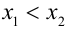
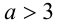
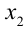
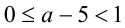
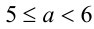
2) Если же , т.е. , то большим является корень , и условие задачи приводит к неравенству , откуда находим .

Ответ: .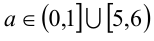

Общая рекомендация такова: если дискриминант квадратного уравнения является полным квадратом и, следовательно, корни имеют рациональный вид, во многих задачах приемлем (часто оказывается проще других методов) стандартный подход. Но если это не так и корни иррациональны, то более удобными могут оказаться специальный метод, эффективность которого была продемонстрирована выше на примерах, и теорема Виета, которые не требуют нахождения корней уравнения в явном виде.

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Квадратные уравнения с параметрами

Ханты-Мансийский автономный округ — Югра

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа №4»

Индекс 628681 Российская Федерация, Тюменская область, Ханты-Мансийский автономный округ – Югра, г. Мегион, /1

Cайт: http//www. megionschool4.ru

Департамент финансов администрации города Мегиона

( МБОУ «Средняя общеобразовательная школа №4»

р/с в РКЦ г. Нижневартовска,

Квадратные уравнения с параметрами

(Методическая разработка для учащихся 9-11 классов)

учитель математики высшей квалификационной категории,

заместитель директора по УВР

1.Теоремы о расположении корней квадратного трехчлена

§2.Применение теоремы Виета

3.Примеры решения задач для подготовки к ГИА и ЕГЭ по математике

Список рекомендованной литературы

В методической разработке систематизированы теоремы о расположении корней квадратного трехчлена (необходимые и достаточные условия расположения корней квадратичной функции относительно заданных точек); особое внимание уделено использованию свойств квадратичной функции; приведено применение теоремы Виета к решению квадратных уравнений с параметрами; все идеи проиллюстрированы примерами, рассмотрены основные методы решения квадратных уравнений с параметрами, подробные методические указания по решению квадратных уравнений с параметрами.

Методическая разработка предназначена для учащихся 9-11 классов, студентов педагогических вузов, а также для учителей. Пособие поможет в подготовке к вступительному экзамену в вуз, сдаче ЕГЭ по математике и к ГИА в новой форме.

Разработка посвящена одному из наиболее трудных разделов элементарной математики: задачам с параметрами. В последние годы в тестах ЕГЭ и ГИА по математике, и на вступительных экзаменах в высшие учебные заведения широкое распространение получили задачи, содержащие параметры. Решение задач с параметрами носит учебно-исследовательский характер, они играют важную роль в формировании логического мышления, развитии творческих способностей учащихся, в формировании научно-исследовательских умений. Задачи с параметрами представляют собой как бы небольшую модель будущей научной работы учащегося. В задачах с параметрами содержится множество приёмов, необходимых не только для математического развития личности, но и и в любом другом научном исследовании. Поэтому решение задач с параметрами и в частности решение квадратных уравнений с параметрами является пропедевтикой научно-исследовательской работы учащихся. На ЕГЭ по математике (часто задания С5), ГИА (задания части 2) и на вступительных экзаменах встречаются, в основном, два типа задач с параметрами. Первый: «Для каждого значения параметра найти все решения некоторого уравнения или неравенства». Второй: «Найти все значения параметра, при каждом из которых для данного уравнения или неравенства выполняются некоторые условия». Соответственно и ответы в задачах этих двух типов различаются по существу. В ответе к задаче первого типа перечисляются все возможные значения параметра и для каждого из этих значений записываются решения уравнения. В ответе к задаче второго типа указываются все значения параметра, при которых выполняются условия, указанные в задаче.

Как известно, решению задач с параметрами в школе уделяется очень мало внимания. Поэтому решение задач с параметрами всегда вызывает большие трудности у учащихся; трудно рассчитывать на то, что учащиеся, подготовка которых не содержала «параметрическую терапию», смогут в жесткой атмосфере конкурсного экзамена успешно справиться с подобными задачами, следовательно, учащиеся должны специально готовиться к «встрече с параметрами». Многие учащиеся воспринимают параметр как «обычное» число. Действительно, в некоторых задачах параметр можно считать постоянной величиной, но это постоянная величина принимает неизвестные значения. Поэтому необходимо рассматривать задачу при всех возможных значениях этой постоянной величины. В других задачах бывает удобно искусственно объявить параметром одну из неизвестных.

Задачи с параметрами обладают диагностической и прогностической ценностью – с помощью задач с параметрами можно проверить знание основных разделов школьной математики, уровень математического и логического мышления, первоначальные навыки научно-исследовательской деятельности, а главное, перспективные возможности успешного овладения курсом математики данного вуза.

Анализ вариантов ЕГЭ по математике и вступительных экзаменов в различные вузы показывает, что большинство предлагаемых задач с параметрами связано с расположением корней квадратного трехчлена. Будучи основной в школьном курсе математики, квадратичная функция формирует обширный класс задач с параметрами, разнообразных по форме и содержанию, но объединенных общей идеей – в основе их решения лежат свойства квадратичной функции. При решении таких задач рекомендуется работать с тремя типами моделей:

1. вербальная модель – словесное описание задачи;

2. геометрическая модель – эскиз графика квадратичной функции;

3. аналитическая модель – система неравенств, при помощи которой описывается геометрическая модель.

Методическое пособие содержит теоремы о расположении корней квадратного трехчлена (необходимые и достаточные условия расположения корней квадратичной функции относительно заданных точек), применение теоремы Виета к решению квадратных уравнений с параметрами. Приведены подробные решения 15 задач с методическими рекомендациями. Назначение данного пособия – помочь выпускнику и учителю математики в подготовке к сдаче ЕГЭ и ГИА по математике, и вступительного экзамена в вуз в виде теста или в традиционной форме.

1. Теоремы о расположении корней квадратного трехчлена

Теоремы о расположении корней квадратного трехчлена не входят непосредственно ни в школьную программу по математике, ни в программу для поступающих в вузы, поэтому выпускник или абитуриент, пользуясь ими, вообще говоря, должен уметь их доказывать. В то же время, обоснование теорем о расположении корней квадратного трехчлена строится на элементарных фактах школьной математики. В данном пособии приведены доказательства нескольких теорем.

Введем следующие обозначения: х1, х2 – корни квадратного трехчлена f(x), х1 ≤ х2, D – дискриминант f(x), xb – абсцисса вершины параболы, являющейся графиком f(x). Решение большинства задач с параметром, в которых необходимо провести исследование квадратного трехчлена, сводится к определению необходимых и достаточных условий реализации одного или нескольких из следующих случаев:

Теорема 1.Для того чтобы оба корня квадратного трехчлена f(x) = ax2 + bx + c (a ≠ 0) были больше некоторого числа n,необходимо и достаточно выполнение следующих условий:

Геометрическая интерпретация. Для того чтобы парабола (см. рис. 1, 2) – график функции f(x) = ax2 + bx + c – пересекала ось ОХ в точках (х1; 0) и (х2; 0), лежащих правее точки (n; 0), необходимо и достаточно выполнения трех условий:

1. вершина параболы – либо лежит в нижней полуплоскости, либо в верхней полуплоскости, либо на оси ОХ ( условие D≥0);

2. ось симметрии параболы – прямая хb = — — лежит правее прямой х = n ( условие xb>n );

3. парабола пересекается с прямой х = n в точке, лежащей в верхней полуплоскости при a>0 и в точке, лежащей в нижней полуплоскости при а 0).

Рис. 1

Доказательство теоремы 1.

Достаточность. Так как D ≥ 0,то по теореме о дискриминанте, получим, что квадратный трехчлен имеет два корня х1 и х2; пусть х1≤х2. Так как вершина параболы расположена между корнями трехчлена, т. е.х1≤хв≤х2, и, по условию, n 0 и уже доказанное неравенство х2 > n:

f(n) = a∙(n – x1)∙(n – x2).

Сравнение знаков левой и правой частей этого неравенства приводит нас к выводу, что выполнено неравенство n – х1 n.

Необходимость. Так как трехчлен имеет два корня, то по теореме о дискриминанте, D≥0. Так как х1> n и х2> n, то х1+х2 > 2n, поэтому

хв = > = n.

По теореме о разложении на линейные множители, с учетом известных по условию знаков, получим запись f(n) = a∙(n – x1)∙(n – x2), из которой следует, что f(n) > 0. Тем самым теорема доказана полностью.

Теорема 2. Для того чтобы оба корня квадратного трехчлена f(х) были меньше некоторого числа m, необходимо и достаточно выполнение следующих условий:

Рис. 3

Рис. 4

Теорема 3.Для того чтобы оба корня квадратного трехчлена f(x) принадлежали заданному промежутку (n; m), необходимо и достаточно выполнение следующих условий:

Рис. 5

Рис. 6

Теорема 4. Только меньший корень квадратного трехчлена f(x) принадлежит заданному промежутку (n; m) тогда и только тогда, когда одновременно выполняются условия:

Рис. 7

Теорема 5. Только больший корень квадратного трехчлена f(x) принадлежит заданному промежутку (n; m) тогда и только тогда, когда одновременно выполняются условия:

Рис. 8

Теорема 6. Для того чтобы оба корня квадратного трехчлена f(x) лежат вне заданного промежутка (n; m), необходимо и достаточно выполнение следующих условий:

Рис. 9

Теорема 7.Для того чтобы один из корней квадратного трехчлена f(x) был больше заданного числа n, а другой меньше, необходимо и достаточно выполнение условия (или для того чтобы некоторое число n лежало между корнями квадратного трехчлена, необходимо и достаточно выполнение условия):

Рис. 10

Теорема 8. Квадратный трехчлен f(x) имеет один корень внутри интервала (n;m), а другой расположен вне этого интервала тогда и только тогда, когда выполняется условие f(n)∙f(m) 6 дискриминант оказывается отрицательным, следовательно, квадратное уравнение не имеет корней.

Ответ: при уравнение не имеет корней; при а = 1 уравнение имеет один корень х = -1; при уравнение имеет два корня ; при а = 2 уравнение имеет единственный корень ; при а = 6 уравнение имеет единственный корень .

Пример 2.При каком значении параметра а уравнение (а — 2)х2 + (4 – 2а)х + 3 = 0 имеет единственный корень?

Решение. Если а = 2, то уравнение превращается в линейное∙х + 3 = 0; которое не имеет корней.

Если а ≠ 2, то уравнение – квадратное и имеет единственный корень при нулевом дискриминанте D.

.

D = 0 при а1 = 2 и a2 = 5. Значение а = 2 исключается, так как противоречит условию, что исходное уравнение – квадратное.

4.При каких значениях параметра а квадратное уравнение

(а — 1)х2 + (2а + 3)х + а + 2 = 0 имеет корни одного знака?

Решение. Так как по условию задачи рассмотренное уравнение – квадратное, значит, а ≠ 1. очевидно, условие задачи предполагает также существование корней квадратного уравнения, что означает неотрицателность дискриминанта

Так как по условию корни должны быть одинаковых знаков, то х1∙х2 > 0, т. е. .Решением последнего неравенства является .С учетом условий D ≥ 0 и а ≠ 1 получим .

Ответ: .

Пример 3.Найти все значения а, для которых уравнение х2 – 2(а – 1)х + (2а + 1) = 0 имеет два положительных корня.

Решение. Из теоремы Виета для того чтобы оба корня х1 и х2 данного уравнения были положительными, необходимо и достаточно, чтобы дискриминант квадратного трехчлена х2 – 2(а – 1)х + (2а + 1) был неотрицательным, а произведение х1∙х2 и сумма х1 + х2 были положительными. Получаем, что все а, удовлетворяющие системе

И только они, являются решениями поставленной задачи. Э та система равносильна системе

Решением которой, а следовательно, и самой задачи являются все числа из промежутка [4; + ∞).

Пример 4.При каких значениях параметра а уравнение (а — 2)х2 — 2(а + 3)х + 4а = 0

имеет два корня, один из которых меньше 2, а другой больше 3?

Решение. По теореме 6, для того чтобы оба корня данного квадратного трехчлена лежали вне заданного промежутка, необходимо и достаточно выполнение условий Получим систему неравенств:

Ответ: .

Пример 5.При каких значениях а уравнение (а — 1)∙х2 = (а + 1)∙х – а имеет единственное решение, удовлетворяющее условию 0 х1. Искомые значения параметра а удобнее найти, решив систему неравенств:

у

Рис.18 0 х1 2 3 х2 5 х

Ответ: (1;3)

Пример 8.При каких значениях параметра а один корень уравнения ах4 – (а — 3)х2 + 3а = 0 меньше –2, три остальных больше –1?

Решение. Пусть х2 = t. Исходя из требований, предъявляемых к корням исходного уравнения, достаточно решить следующую задачу: при каких значениях а один корень уравнения at2 – (a — 3)t + 3a = 0 больше 4, другой меньше 1, но не меньше 0? Очевидно а ¹ 0, D > 0. Представим уравнение в виде:

.

Его корни будут удовлетворять указанным выше условиям, если f(1) 0. Поскольку f(0) = 3, то достаточно решить систему

Решением уравнения является . Ответ: .

Пример 9.Найдите все значения параметра а, при которых все корни уравнения

(2 — а)х2 – 3ах + 2а = 0 больше .

Решение. Введем обозначения f(x) = (2 — a)x2 – 3ax + 2a, ;

Если а = 2, то . для случая а ≠ 2, чтобы сформулировать нужные условия, представим себе график трехчлена f(x), оба корня которого больше .

(к рис.19) (к рис.20)

(к рис.21) (к рис.22)

Объединяя эти условия, получим систему:

Ответ: .

Пример 10. Найти все значения а, при которых уравнение cos8x + sin8x = a имеет корни, и решить это уравнение.

Решение. Используя равенства cos8x + sin8x = (cos4x – sin4x)2 + 2cos4x×sin4x = cos22x + и полагая cos 4x = t, преобразуем исходное уравнение к виду t2 + 14t + 17 – 32a = 0. Задача сводится к нахождению тех значений а при которых последнее уравнение имеет действительные корни такие, что хотя один из них удовлетворяет условию . Имеем дискриминант уравнения:

и неравенство D1 ³ 0 выполняется при а ³ -1. находим корни t1 и t2 уравнения :

; .

Заметим, что t1 1.

Первый случай реализуется неравенством D = -4a + 5