Точка пересечения прямой и плоскости онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямой и плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямой и плоскости задайте вид уравнения прямой («канонический» или «параметрический» ), введите данные в уравнения прямой и плоскости и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Точка пересечения прямой и плоскости − теория, примеры и решения
- Содержание
- 1. Точка пересечения плоскости и прямой, заданной в каноническом виде.
- 2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
- 3. Примеры нахождения точки пересечения прямой и плоскости.
1. Точка пересечения плоскости и прямой, заданной в каноническом виде
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямая L1:
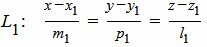 , , | (1) |
| α: Ax+By+Cz+D=0. | (2) |
Найти точку пересечения прямой L1 и плоскости α (Рис.1).
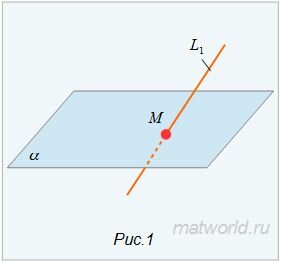 |
Запишем уравнение (1) в виде системы двух линейных уравнений:
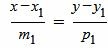 , , | (3) |
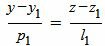 | (4) |
Сделаем перекрестное умножение в уравнениях (3) и (4):
| p1(x−x1)=m1(y−y1) |
| l1(y−y1)=p1(z−z1) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p1x−m1y=p1x1−m1y1, | (5) |
| l1y−p1z=l1y1−p1z1. | (6) |
Решим систему линейных уравнений (2), (5), (6) с тремя неизвестными x, y, z. Для этого в уравнении (2) переведем свободный член в правую часть уравнения и запишем эту систему в матричном виде:
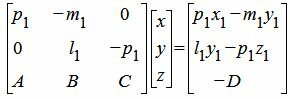 | (7) |
Как решить систему линейных уравнений (11)(или (2), (5), (6)) посмотрите на странице Метод Гаусса онлайн или на примерах ниже. Если система линейных уравнениий (7) несовместна, то прямая L1 и плоскость α не пересекаются. Если система (7) имеет множество решений, то прямая L1 лежит на плоскости α. Единственное решение системы линейных уравнений (7) указывает на то, что это решение определяет координаты точки пересечения прямой L1 и плоскости α.
Замечание. Если прямая задана параметрическим уравнением, то уранение прямой нужно приводить к каноническому виду и применить метод, описанный выше, или же
2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L1 в параметрическом виде:
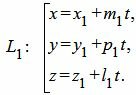 | (8) |
| α: Ax+By+Cz+D=0. | (9) |
Задачу нахождения нахождения точки пересечения прямых L1 и плоскости α можно решить разными методами.
Метод 1. Приведем уравнения прямой L1 к каноническому виду.
Для приведения уравнения (8) к каноническому виду, выразим параметр t через остальные переменные:
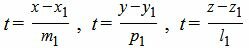 | (10) |
Так как левые части уравнений (10) равны, то можем записать:
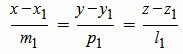 | (11) |
Далее, для нахождения точки пересечения прямой и плоскости нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямой L1 и плоскости α решим совместно уравнения (8) и (9). Из уравнений (8) подставим x, y, z в (9):
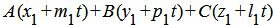 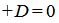 | (13) |
Откроем скобки и найдем t:
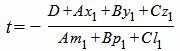 | (14) |
Если числитель и знаменатель в уравнении (14) одновременно равны нулю, то это значит, что прямая L1 лежит на полскости α. Если в уравнении (14) числитель отличен от нуля, а знаменатель равен нулю, то прямая и плоскость параллельны.
Если же числитель и знаменатель в уравнении (14) отличны от нуля, то прямая и плоскость пересекаются в одной точке. Для нахождения координат точки пересечения прямой L1 и плоскости α подставим полученное значение t из (14) в (8).
3. Примеры нахождения точки пересечения прямой и плоскости.
Пример 1. Найти точку пересечения прямой L1:
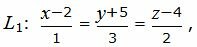 | (15) |
| α: 7x−5y+2z+19=0. | (16) |
Представим уравнение (15) в виде двух уравнений:
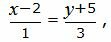 | (17) |
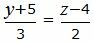 | (18) |
Сделаем перекрестное умножение в уравнениях (17) и (18):
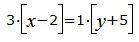 |
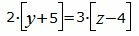 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
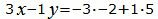 |
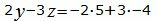 |
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (19) и (20). Для этого переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (19) и (20):
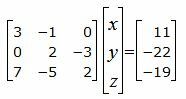 | (21) |
Решим систему линейных уравнений (21) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
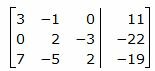 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −7/3:
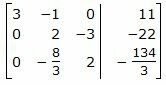 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на 4/3:
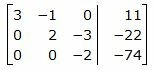 |
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −3/2:
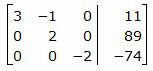 |
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 1/2:
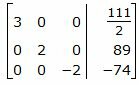 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
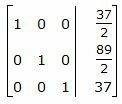 |
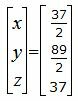 |
Ответ. Точка пересечения прямой L1 и плоскости α имеет следующие координаты:
| M (37/2, 89/2, 37). |
Пример 2. Найти точку пересечения прямой L1:
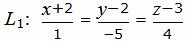 | (22) |
| α: 6x+2y+z+7=0. | (23) |
Представим уравнение (22) в виде двух уравнений:
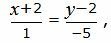 | (24) |
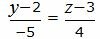 | (25) |
Сделаем перекрестное умножение в уравнениях (24) и (25):
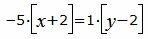 |
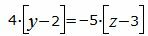 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
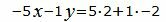 |
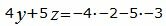 |
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (26) и (27). Переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (26) и (27):
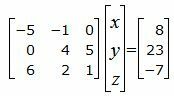 | (28) |
Решим систему линейных уравнений (21) отностительно x, y, z. Для этого построим расширенную матрицу:
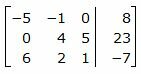 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 3 со строкой 1, умноженной на 6/5:
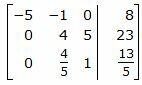 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на −1/5:
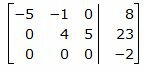 |
Из расширенной матрицы восстановим систему линейных уравнений:
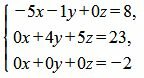 | (29) |
Легко можно заметить, что последнее уравнение в (29) несовместна, так как несуществуют такие x, y, z чтобы выполнялось это равенство. Следовательно система линейных уравнений (2), (26) и (27) несовместна. Тогда прямая L1 и плоскость α не пересекаются, т.е. они параллельны.
Ответ. Прямая L1 и плоскость α параллельны, т.е. не имеют общую точку.
Пример 3. Найти точку пересечения прямой в параметрическом виде L1:
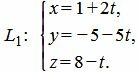 | (30) |
| α: 2x+y−z+11=0. | (31) |
Решение. Для нахождения точки пересечения прямой L1 и плоскости α нужно найти такое значение t, при котором точка M(x, y, z) удовлетворяет уравнению (31). Поэтому подставим значения x, y, z из (30) в (31):
| 2(1+2t)+(−5−5t)−(8−t)+11=0. |
| 2+4t−5−5t−8+t+11=0. | (32) |
Упростив уравнение, получим:
Как видим, любое значение t удовлетворяет уравнению (33), т.е. любая точка на прямой L1 удовлетворяет уравнению плоскости α. Следовательно прямая L1 лежит на плоскости α.
Ответ. Прямая L1 лежит на плоскости α.
Взаимное расположение прямой и плоскости в пространстве.
Признак параллельности прямой и плоскости
Все возможные случаи взаимного расположения прямой и плоскости в пространстве представлены в следующей таблице.
| Фигура | Рисунок | Формулировка | ||||||||||
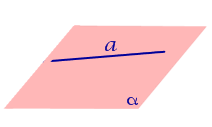
| Прямая лежит на плоскости (принадлежит плоскости) |  | |||||||||||
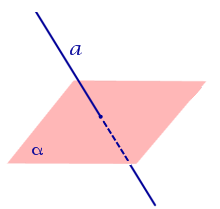
| Прямая пересекает плоскость | 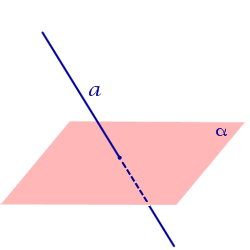 | |||||||||||
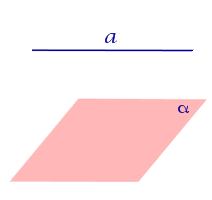
| Прямая параллельна плоскости | 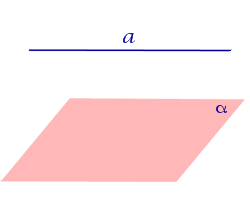 |
| Прямая лежит на плоскости (принадлежит плоскости) | |
| Прямая пересекает плоскость | |
| Прямая параллельна плоскости | |
 |
 |
| Рис.1 |
 |
| Рис.2 |
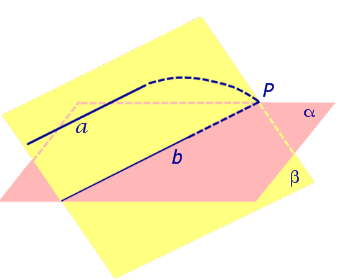
Доказательство . Рассмотрим случай 2 и предположим противное. Предположим, что прямые a и b пересекаются в некоторой точке P (рис.3) .
Но тогда точка P оказывается точкой пересечения прямой a и плоскости α , и мы получаем противоречие с тем, что прямая a и плоскость α параллельны. Полученное противоречие и завершает доказательство утверждения 1.
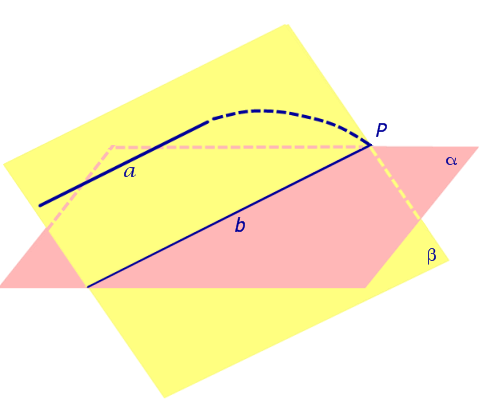
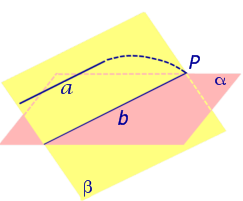
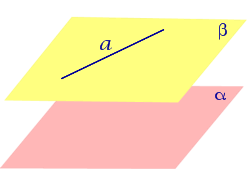
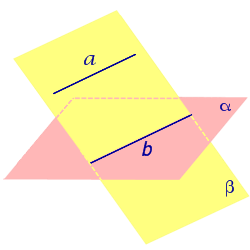
Утверждение 2 (признак параллельности прямой и плоскости) . Если прямая a , не лежащая в плоскости α , параллельна некоторой прямой b , лежащей в плоскости α , то прямая a и плоскость α параллельны.
Доказательство. Докажем признак параллельности прямой и плоскости «от противного». Предположим, что прямая a пересекает плоскость α в некоторой точке P . Проведем плоскость β через параллельные прямые a и b Проведем плоскость β через параллельные прямые a и b (рис. 4).
Точка P лежит на прямой a и принадлежит плоскости β. Но по предположению точка P принадлежит и плоскости α , следовательно точка P лежит на прямой b , по которой пересекаются плоскости α и β . Однако прямые a и b параллельны по условию и не могут иметь общих точек.
Полученное противоречие завершает доказательство признака параллельности прямой и плоскости.
Прямая, плоскость и их уравнения
Начальные сведения
Введено понятие прямой, показаны принятые обозначения, рассмотрены варианты взаимного расположения прямой и точки, двух прямых, перечислены способы задания прямой на плоскости.
Получите представление о прямой линии в пространстве, рассмотрите варианты взаимного расположения прямых и способы задания прямой в пространстве.
Дано понятие плоскости в трехмерном пространстве, представлены варианты ее взаимного расположения с точкой, прямой и другой плоскостью, показаны способы задания.
Уравнения прямой на плоскости
Что называют уравнением прямой и какие виды уравнения прямой на плоскости существуют? В этой статье Вы найдете ответы на эти вопросы.
Познакомьтесь с направляющим вектором прямой, узнайте как его координаты участвуют в записи уравнения прямой.
Узнайте что такое нормальный вектор прямой и как определяются его координаты по уравнению прямой на плоскости.
Всесторонне разобрано общее уравнение прямой, показаны неполные уравнения, приведены примеры и графические иллюстрации.
Научитесь работать с каноническими уравнениями прямой, разберитесь как в их записи участвуют координаты направляющего вектора прямой, рассмотрите решения характерных задач.
Откройте для себя уравнение прямой в отрезках, узнайте почему оно получило такое название и почему с помощью уравнения этого вида легко построить прямую с прямоугольной системе координат.
Рассмотрено уравнение прямой с угловым коэффициентом, введены определения угла наклона и углового коэффициента, разобраны решения характерных задач на составление уравнений прямой этого вида.
Познакомьтесь с параметрическими уравнениями прямой на плоскости, научитесь от уравнений прямой другого вида переходить к параметрическим уравнениями и обратно.
Узнайте как выводится нормальное уравнение прямой и как оно применяется для нахождения расстояния от точки до прямой.
Уравнения плоскости
Узнайте какими уравнениями описываются плоскости в прямоугольной системе координат в трехмерном пространстве.
Запомните определение нормального вектора плоскости, посмотрите как его координаты участвуют в записи уравнений плоскости.
Познакомьтесь с полными и неполными общими уравнениями плоскости, рассмотрите примеры и решения характерных задач.
Показано как из общего уравнения плоскости получить уравнение плоскости в отрезках и как его использовать для построения плоскости.
Разобрано как нормальное (нормированное) уравнение плоскости получается из общего и как оно применяется для нахождения расстояния от точки до плоскости.
Уравнения прямой в пространстве
Показано с помощью каких уравнений можно задать прямую линию в пространстве в заданной прямоугольной системе координат.
Разобрано как прямая линия в прямоугольной системе координат в пространстве задается уравнениями двух пересекающихся плоскостей.
Познакомьтесь с параметрическими уравнениями прямой в пространстве, рассмотрите примеры их составления и способы перехода к уравнениям другого вида.
Подробно рассмотрены канонические уравнения прямой в пространстве, показана их связь с другими видами уравнений, приведены решения характерных примеров и задач.
Параллельность и перпендикулярность
Даны основные сведения о параллельных прямых, перечислены признаки и условия параллельности прямых в том числе через направляющие и нормальные векторы.
Приведены начальные сведения о перпендикулярных прямых, разобраны признаки и условия перпендикулярности прямых.
Получите основные сведения о параллельных прямой и плоскости, научитесь выяснять параллельны ли прямая и плоскость.
Примите к сведению условия и признаки перпендикулярности прямой и плоскости, ознакомьтесь с решением характерных примеров.
Познакомьтесь с определением параллельных плоскостей и с условиями параллельности, разберите решения характерных примеров и задач.
Приведены признаки и условия перпендикулярности плоскостей, позволяющие устанавливать параллельны ли плоскости, заданные своими уравнениями.
Составление уравнений прямой
Научитесь составлять уравнение прямой, когда известны координаты двух лежащих на ней точек, в этом Вам помогут прведенные решения примеров с пояснениями.
Узнайте как составляются уравнения прямой, когда известны уравнения параллельной ей прямой и координаты точки, через которую она проходит.
Разберитесь с составлением уравнений прямой, проходящей через данную точку перпендикулярно заданной прямой, рассмотрите решения характерных примеров.
Познакомьтесь с принципом составления уравнений прямой, которая проходит через заданную точку перпендикулярно заданной плоскости.
Показана суть составления уравнений прямой для данных условий, приведены готовые решения примеров.
Составление уравнений плоскости
Узнайте как составляется уравнение плоскости, когда даны координаты трех ее точек, рассмотрите решения примеров.
На примерах показано как составить уравнение плоскости, когда известно уравнение лежащей на ней прямой и координаты точки.
Научитесь записывать уравнение плоскости, которая проходит через две заданные параллельные или пересекающиеся прямые.
Показано как составляется уравнение плоскости, если известны координаты одной ее точки и уравнение прямой, которой она перпендикулярна.
Разберитесь с составлением уравнения плоскости, когда известны координаты точки, через которую она проходит, и уравнение плоскости, которой она параллельна.
Показаны примеры составления уравнения плоскости, которая перпендикулярна двум заданным плоскостям и проходит через заданную точку.
Нахождение углов методом координат
Получена формула для нахождения косинуса угла и самого угла между пересекающимися прямыми, показаны решения примеров.
Дано определение угла между скрещивающимися прямыми и разобрано как находить этот угол методом координат.
Узнайте как находить угол между прямой и плоскостью когда известны их уравнения, разберитесь в решениях характерных примеров.
Разберитесь с нахождением угла между пересекающимися плоскостями, запомните формулу и рассмотрите приведенные решения примеров.
Нахождение координат точек пересечения
Узнайте как находить координаты точки пересечения двух прямых на плоскости и в пространстве, разберите решения характерных задач.
На примерах показаны способы нахождения координат точки пересечения прямой и плоскости.
Нахождение расстояний методом координат
Разобраны различные способы нахождения расстояния от заданной точки до заданной прямой, в том числе с использованием нормального уравнения прямой, приведены решения примеров.
Научитесь находить расстояние от точки до плоскости методом координат, для этого удобно использовать нормальное уравнение плоскости.
Познакомьтесь со способами нахождения расстояния между параллельными прямыми в прямоугольной системе координат.
Узнайте как определяется расстояние между скрещивающимися прямыми, разберите примеры нахождения расстояния методом координат.
Показано как находить расстояние между прямой и плоскостью, которые параллельны, для пояснения приведены решения примеров.
Разберитесь с нахождением расстояния между параллельными плоскостями, когда известны их уравнения.
Связки и пучки
Узнайте что такое пучок прямых, рассмотрите его уравнение и связанные с пучками прямых характерные примеры.
Познакомьтесь с пучком плоскостей и видом уравнения пучка плоскостей.
Дано определение связки плоскостей и ее уравнение, показаны решения примеров.
Проекция точки на прямую и плоскость
Узнайте что называют проекцией точки на прямую и как находятся координаты проекции.
Показано как находить координаты проекции точки на плоскость, разобраны решения примеров.
http://www.resolventa.ru/demo/fiz/trege.htm
http://www.cleverstudents.ru/line_and_plane/index.html