Расстояние между прямыми в пространстве онлайн
С помощю этого онлайн калькулятора можно найти расстояние между прямыми в пространстве. Дается подробное решение с пояснениями. Для вычисления расстояния между прямыми в пространстве, задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние между прямыми в пространстве − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
 . . | (1) |
 , , | (2) |
Прямые (1) и (2) в пространстве могут совпадать, быть паралленьными, пересекаться, или быть скрещивающимся. Если прямые в пространстве пересекаются или совпадают, то расстояние между ними равно нулю. Мы рассмотрим два случая. Первый − прямые параллельны, и второй − прямые скрещиваются. Остальные являются частыми случаями. Если при вычислении расстояния между параллельными прямыми мы получим расстояние равным нулю, то это значит, что эти прямые совпадают. Если же расстояние между скрещивающимися прямыми равно нулю, то эти прямые пересекаются.
1. Расстояние между параллельными прямыми в пространстве
Рассмотрим два метода вычисления расстояния между прямыми.
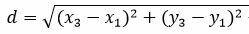  |
которое и является расстоянием между прямыми L1 и L2 (Рис.1).
 |
Пример 1. Найти расстояние между прямыми L1 и L2:
 | (3) |
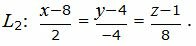 | (4) |
| q1=<m1, p1, l1>= |
| q2=<m2, p2, l2>= |
Найдем проекцию точки M1 на прямую L2. Для этого построим плоскость α, проходящей через точку M1 и перпендикулярной прямойL2.
Для того, чтобы плоскость α было перепендикулярна прямой L2, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L2, т.е. в качестве нормального вектора плоскости α можно взять направляющий вектор прямой L2. Тогда уравнение искомой плоскости, проходящей через точку M1(x1, y1, z1) имеет следующий вид:
| m2<x−x1)+p2(y−y1)+ l2(z−z1)=0 | (5) |
| 2(x−1)−4(y−2)+ 8(z−1)=0 |
После упрощения получим уравнение плоскости, проходящей через точку M1 и перпендикулярной прямой L2:
| 2x−4y+ 8z−2=0 | (6) |
Найдем точку пересечения прямой L2 и плоскости α, для этого построим параметрическое уравнение прямой L2.
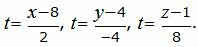 |
Выразив переменные x, y, z через параметр t, получим параметрическое уравнение прямой L2:
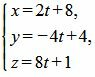 | (7) |
Чтобы найти точку пересечения прямой L2 и плоскости α, подставим значения переменных x, y, z из (7) в (6):
 |
Решив уравнение получим:
 | (8) |
Подставляя полученное значение t в (7), получим точку пересеченияпрямой L2 и плоскости α:
 |
Остается найти расстояние между точками M1 и M3:
 |
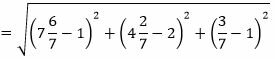  |
Ответ: Расстояние между прямыми L1 и L2 равно d=7.2506.
Метод 2. Найдем расстояние между прямыми L1 и L2 (уравнения (1) и (2)). Во первых, проверяем параллельность прямых L1 и L2. Если направляющие векторы прямых L1 и L2 коллинеарны, т.е. если существует такое число λ, что выполнено равенство q1=λq2, то прямые L1 и L2 параллельны.
Данный метод вычисления расстояния между параллельными векторами основана на понятии векторного произведения векторов. Известно, что норма векторного произведения векторов 
 |
Вычислим координаты вектора 
 |
Вычислим векторное произведение векторов 
 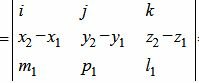 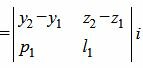  |
Вычисляя определители второго порядка находим координаты вектора c:
Далее находим площадь параллелограмма:
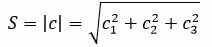 . . |
Расстояние между прямыми L1 и L2 равно:
 , , |
 , , |
Пример 2. Решим пример 1 методом 2. Найти расстояние между прямыми
 | (25) |
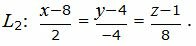 | (26) |
| q1=<m1, p1, l1>= |
| q2=<m2, p2, l2>= |
Векторы q1 и q2 коллинеарны. Следовательно прямые L1 и L2 параллельны. Для вычисления расстояния между параллельными прямыми воспользуемся векторным произведением векторов.
Построим вектор 
Вычислим векторное произведение векторов 

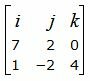 |
Вычислим определитель этой матрицы, разложив ее по первой строке. Результатом этих вычислений получим векторное произведение векторов 
   |
Таким образом, результатом векторного произведения векторов 
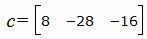 |
Поскольку векторное произведение векторов 
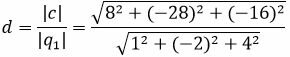  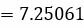 |
Ответ: Расстояние между прямыми L1 и L2 равно d=7.25061.
2. Расстояние между скрещивающимися прямыми в пространстве
Пусть задана декартова прямоугольная симтема координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 (уравнения (1) и (2)).
Пусть прямые L1 и L2 не параллельны (паралельные прямые мы расстотрели в предыдущем параграфе). Чтобы найти расстояние между прямыми L1 и L2 нужно построить параллельные плоскости α1 и α2 так, чтобы прямая L1 лежал на плоскости α1 а прямая L2 − на плоскости α2. Тогда расстояние между прямыми L1 и L2 равно расстоянию между плоскостями L1 и L2 (Рис. 3).
 |
Поскольку плоскость α1, проходит через прямую L1, то он проходит также через M1(x1, y1, z1). Следовательно справедливо следующее равенство:
| A1x1+B1y1+C1z1+D1=0. | (27) |
где n1=<A1, B1, C1> − нормальный вектор плоскости α1. Для того, чтобы плоскость α1 проходила через прямую L1, нормальный вектор n1 должен быть ортогональным направляющему вектору q1 прямой L1, т.е. скалярное произведение этих векторов должен быть равным нулю:
| A1m1+B1p1+C1l1=0. | (28) |
Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:
| A1m2+B1p2+C1l2=0. | (29) |
Решая систему линейных уравнений (27)−(29), с тремя уравнениями и четыремя неизвестными A1, B1, C1, D1, и подставляя в уравнение
| A1x+B1y+C1z+D1=0. | (30) |
получим уравнение плоскости α1. (Как построить уравнение плоскости, проходящей через прямую, параллельно другой прямой подробно изложено здесь).
Аналогичным образом находим уравнение плоскости α2:
| A2x+B2y+C2z+D2=0. | (31) |
Плоскости α1 и α2 параллельны, следовательно полученные нормальные векторыn1=<A1, B1, C1> и n2=<A2, B2, C2> этих плоскостей коллинеарны. Если эти векторы не равны, то можно умножить (31) на некторое число так, чтобы полученный нормальный вектор n2 совпадал с нормальным вектором уравнения (30).
Тогда расстояние между параллельными плоскостями вычисляется формулой:
 . . |
Полученное расстояние между плоскостями α1 и α2 является также расстоянием между прямыми L1 и L2.
Пример 3. Найти расстояние между прямыми
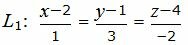 | (32) |
 | (33) |
Построим плоскость α1, проходящую через прямую L1, параллельно прямой L2.
Поскольку плоскость α1 проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(2, 1, 4) и нормальный вектор n1=<m1, p1, l1> плоскости α1 перпендикулярна направляющему вектору q1 прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
| A1x1+B1y1+C1z1+D1=0. | (34) |
а условие параллельности прямой L1 и искомой плоскости α1 представляется следующим условием:
| A1m1+B1p1+C1l1=0. | (35) |
Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:
| A1m2+B1p2+C1l2=0. | (36) |
| A1·2+B1·1+C1·4+D1=0. | (37) |
| A1·1+B1·3+C1·(−2)=0. | (38) |
| A1·2+B1·(−3)+C1·7=0. | (39) |
Представим эти уравнения в матричном виде:
 | (40) |
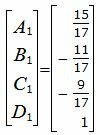 | (41) |
Искомая плоскость может быть представлена формулой:
| A1x+B1y+C1z+D1=0. | (42) |
 |
Упростим уравнение, умножив на число 17.
 | (43) |
Построим плоскость α2, проходящую через прямую L2, параллельно прямой L1.
Поскольку плоскость α2 проходит через прямую L2 , то она проходит также через точку M2(x2, y2, z2)=M2(6, −1, 2) и нормальный вектор n2=<m2, p2, l2> плоскости α2 перпендикулярна направляющему вектору q2 прямой L2. Тогда уравнение плоскости должна удовлетворять условию:
| A2x2+B2y2+C2z2+D2=0. | (44) |
а условие параллельности прямой L2 и искомой плоскости α2 представляется следующим условием:
| A2m2+B2p2+C2l2=0. | (45) |
Так как плоскость α2 должна быть параллельной прямой L1, то должна выполнятся условие:
| A2m1+B2p1+C2l1=0. | (46) |
| A1·6+B1·(−1)+C1·2+D1=0. | (47) |
| A1·2+B1·(−3)+C1·7=0. | (48) |
| A1·1+B1·3+C1·(−2)=0. | (49) |
Представим эти уравнения в матричном виде:
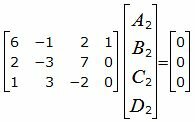 | (50) |
 | (51) |
Искомая плоскость может быть представлена формулой:
| A2x+B2y+C2z+D2=0. | (52) |
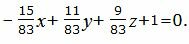 |
Упростим уравнение, умножив на число −83.
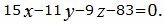 | (53) |
Расстояние между построенными плоскостями (43) и (53) будет расстоянием между прямыми (1) и (2).
Запишем формулы уравнений плоскостей α1 и α2 :
| A1x+B1y+C1z+D1=0. |
| A2x+B2y+C2z+D2=0. |
Поскольку нормальные векторы плоскостей α1 и α2 совпадают, то можно найти расстояние между плоскостями α1 и α2, используя следующую формулу:
 | (54) |
 |
Упростим и решим:
 |
Расстояние между прямыми равно: d=4.839339
Расстояние между скрещивающимися прямыми: формула
Вы будете перенаправлены на Автор24
Скрещивающиеся прямые — это прямые, не лежащие в одной плоскости и не пересекающиеся между собой.
Наименьшим расстоянием между двумя скрещивающимися прямыми является перпендикуляр, опущенный с одной прямой на другую. У каждой пары скрещивающихся прямых при этом есть только один такой общий перпендикуляр.
Рисунок 1. Кратчайшее расстояние между скрещивающимися прямыми. Автор24 — интернет-биржа студенческих работ
Через каждую из скрещивающихся прямых возможно провести лишь одну плоскость, параллельную второй скрещивающейся прямой, соответственно, для определения расстояния между скрещивающимися прямыми, достаточно определить расстояние между одной из скрещивающихся прямых и плоскостью, на которой лежит вторая прямая.
Соответственно, задачу поиска расстояния между прямой и параллельной ей плоскостью можно свести к поиску расстояния между любой точкой, лежащей на вышеозначенной прямой, и плоскостью.
Как найти расстояние между скрещивающимися прямыми: координатный метод
Рассмотрим методику нахождения расстояния между двумя скрещивающимися прямыми $L_1$ и $L_2$ через координатный метод.
Прежде всего необходимо найти уравнение плоскости $β$, параллельной прямой $L_1$. Для этого необходимо найти векторное произведение направляющих векторов прямых $L_1$ и $L_2$, данное произведение представляет собой координаты нормального вектора плоскости $β$:
При вычислении выражения $(1)$ мы получим коэффициенты для общего уравнения плоскости $β$ — $A, B$ и $C$.
Готовые работы на аналогичную тему
Для того чтобы записать всё общее выражение плоскости, подставим координаты любой точки, лежащей на $L_2$ в общую форму, например, можно подставить точку с координатами $(x_2;y_2; z_2)$, получим следующее:
$A (x-x_2) + B (y – y_2) + C(z- z_2) + D=0$.
Теперь достаточно выбрать любую точку на прямой $L_1$, пусть это будет точка $M_1$ с координатами $(x_1;y_1; z_1)$.
Расстояние от плоскости $β$ до точки $M_1$ составит:
где $A, B, C$ и $D$ — коэффициенты уравнения плоскости $β$, а $(x_1;y_1; z_1)$ — координаты точки, лежащей на прямой $L_1$.
Данная формула позволяет высчитать расстояние между двумя скрещивающимися прямыми.
Определить расстояние между скрещивающимися прямыми $L_1$ и $L_2$.
Найдём нормальный вектор плоскости, в которой лежит прямая $L_2$, для этого выпишем направляющие вектора для каждой из прямых:
$L_1: \vec
$L_2: \vec
Теперь найдём векторное произведение векторов $\vec
$[\vec
Подставим координаты точки $(-1;0;1)$, принадлежащей прямой $L_2$, в общее уравнение плоскости:
$-2 \cdot (x+1) + (y-0) – 1 \cdot(z-1)=0$
Упрощаем и в конечном итоге имеем следующее уравнение плоскости:
Теперь, используя координаты точки $(2;-1;0)$, лежащей на первой прямой, можно воспользоваться формулой $(2)$ для вычисления расстояния между двумя скрещивающимися прямыми:
Координатная формула вычисления расстояния между скрещивающимися прямыми
Также аналогичное уравнение для поиска расстояния между скрещивающимися прямыми можно использовать сразу в полной координатной форме:
$ρ=\frac<\begin
Для того чтобы воспользоваться данной формулой, возможно нужно освежить в памяти способы нахождения определителей матриц.
Найти расстояние между вышеприведёнными прямыми с помощью формулы $(3)$.
Выпишем сначала точки, принадлежащие данным прямым и их направляющие векторы:
$L_1$ имеет направляющий вектор $\<2; -3; -1\>$, а принадлежащая ей точка имеет координаты $(2; -1; 0)$.
$L_2$ имеет направляющий вектор $\<1; -2; 0 \>$, а принадлежащая ей точка имеет координаты $(-1; 0; 1)$.
Воспользуемся формулой $(3)$:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 06 03 2021
Расстояние между скрещивающимися прямыми: определение и примеры нахождения
Статья нацелена на нахождение расстояния между скрещивающимися прямыми методом координат. Будет рассмотрено определение расстояния между этими прямыми, получим алгоритм при помощи которого преобразуем нахождение расстояния между скрещивающимися прямыми. Закрепим тему решением подобных примеров.
Расстояние между скрещивающимися прямыми – определение
Предварительно необходимо доказать теорему, которая определяет связь между заданными скрещивающимися прямыми.
Раздел взаимного расположения прямых в пространстве говорит о том, что если две прямые называют скрещивающимися, если их расположение не в одной плоскости.
Через каждую пару скрещивающихся прямых может проходить плоскость, параллельная данной, причем только одна.
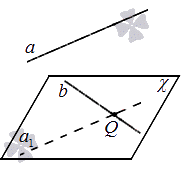
По условию нам даны скрещивающиеся прямые a и b . Необходимо доказать проходимость единственной плоскости через прямую b , параллельную данной прямой a . Аналогичное доказательство необходимо применять для прямой a , через которую проходит плоскость, параллельная данной прямой b .
Для начала необходимо отметить точку Q на прямой b . Если следовать из определения параллельности прямых, то получаем, что через точку пространства можно провести прямую, параллельную заданной прямой, причем только одну. Значит, через точку Q проходит только одна прямая, параллельная прямой a . Примем обозначение а а 1 .
Раздел способов задания плоскости было говорено о том, что прохождение единственной плоскости возможно через две пересекающиеся прямые. Значит, получаем, что прямые b и а 1 – пересекающиеся прямые, через которые проходит плоскость, обозначаемая χ .
Исходя из признака параллельности прямой с плоскостью, можно сделать вывод, что заданная прямая a параллельна относительно плоскости χ , потому как прямая a параллельна прямой а 1 , расположенной в плоскости χ .
Плоскость χ является единственной, так как прямая, проходящая через заданную прямую, находящуюся в пространстве, параллельна заданной прямой. Рассмотрим на рисунке, предоставленном ниже.
При переходе от определения расстояния между скрещивающимися прямыми определяем расстояние через расстояние между прямой и параллельной ей плоскостью.
Расстоянием между скрещивающимися прямыми называют расстояние между одной из скрещивающихся прямых и параллельной ей плоскостью, проходящей через другую прямую.
То есть расстояние между прямой и плоскостью является расстоянием от заданной точки к плоскости. Тогда применима формулировка определения расстояния между скрещивающимися прямыми.
Расстоянием между скрещивающимися прямыми называют расстояние от некоторой точки скрещивающихся прямых к плоскости, проходящей через другую прямую, параллельную первой прямой.
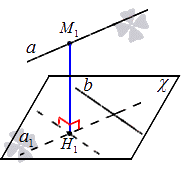
Произведем подробное рассмотрение прямых a и b . Точка М 1 располагается на прямой a , через прямую b проводится плоскость χ , параллельная прямой a . Из точки М 1 проводим перпендикуляр М 1 Н 1 к плоскости χ . Длина этого перпендикуляра является расстоянием между скрещивающимися прямыми a и b . Рассмотрим на рисунке, приведенном ниже.
Нахождение расстояния между скрещивающимися прямыми – теория, примеры, решения
Расстояния между скрещивающимися прямыми находятся при построении отрезка. Искомое расстояние равняется длине этого отрезка. По условию задачи его длина находится по теореме Пифагора, по признакам равенства или подобия треугольников или другим.
Когда имеем трехмерное пространство с системой координат О х у z с заданными в ней прямыми a и b , то вычисления следует проводить, начиная с расстояния между заданными скрещивающимися при помощи метода координат. Произведем подробное рассмотрение.
Пусть по условию χ является плоскостью, проходящей через прямую b , которая параллельна прямой a . Искомое расстояние между скрещивающимися прямыми a и b равняется расстоянию от точки М 1 , расположенной на прямой a , к плоскости _ χ . Для того, чтобы получить нормальное уравнение плоскости χ , необходимо определить координаты точки M 1 ( x 1 , y 1 , z 1 ) , расположенной на прямой a . Тогда получим cos α · x + cos β · y + cos γ · z — p = 0 , которое необходимо для определения расстояния M 1 H 1 от точки M 1 x 1 , y 1 , z 1 к плоскости χ . Вычисления производятся по формуле M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p . Необходимое расстояние равняется искомому расстоянию между скрещивающимися прямыми.
Данная задача предполагает получение координат точки М 1 , которая располагается на прямой a , нахождение нормального уравнения плоскости χ .
Определение координат точки М 1 необходимо и возможно при знании основных видов уравнений прямой в пространстве. Чтобы получить уравнение плоскости χ , необходимо остановиться подробней на алгоритме вычисления.
Если координаты x 2 , y 2 , z 2 будут определены при помощи точки М 2 , через которую проведена плоскость χ , получаем нормальный вектор плоскости χ в виде вектора n → = ( A , B , C ) . Следуя из этого, можно записать общее уравнение плоскости χ в виде A · x — x 2 + B · ( y — y 2 ) + C · ( z — z 2 ) = 0 .
Вместо точки М 2 может быть взята любая другая точка, принадлежащая прямой b , потому как плоскость χ проходит через нее. Значит, координаты точки М 2 найдены. Необходимо перейти к нахождению нормального вектора плоскости χ .
Имеем, что плоскость χ проходит через прямую b , причем параллельна прямой a . Значит, нормальный вектор плоскости χ перпендикулярен направляющему вектору прямой a , обозначим a → , и направляющему вектору прямой b , обозначим b → . Вектор n → будет равняться векторному произведению a → и b → , что значит, n → = a → × b → . После определения координат a x , a y , a z и b x , b y , b z направляющих векторов заданных прямых a и b , вычисляем
n → = a → × b → = i → j → k → a x a y a z b x b y b z
Отсюда находим значение координат A , B , C нормального вектора к плоскости χ .
Знаем, что общее уравнение плоскости χ имеет вид A · ( x — x 2 ) + B · ( y — y 2 ) + C · ( z — z 2 ) = 0 .
Необходимо привести уравнение к нормальному виду cos α · x + cos β · y + cos γ · z — p = 0 . После чего нужно произвести вычисления искомого расстояния между скрещивающимися прямыми a и b , исходя из формулы M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p .
Чтобы найти расстояние между скрещивающимися прямыми a и b , необходимо следовать алгоритму:
- определение координат ( x 1 , y 1 , z 1 ) и x 2 , y 2 , z 2 точек М 1 и М 2 , расположенных на прямых a и b соответственно;
- получение координат a x , a y , a z и b x , b y , b z , принадлежащих направляющим векторам прямых a и b ;
- нахождение координат A , B , C , принадлежащих вектору n → на плоскости χ , проходящей через прямую b , расположенную параллельно a , по равенству n → = a → × b → = i → j → k → a x a y a z b x b y b z ;
- запись общего уравнения плоскости χ в виде A · x — x 2 + B · ( y — y 2 ) + C · ( z — z 2 ) = 0 ;
- приведение полученного уравнения плоскости χ к уравнению нормального вида cos α · x + cos β · y + cos γ · z — p = 0 ;
- вычисление расстояния M 1 H 1 от M 1 x 1 , y 1 , z 1 к плоскости χ , исходя из формулы M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p .
Пример 1
Имеются две скрещивающиеся прямые в прямоугольной системе координат О х у z трехмерного пространства. Прямая a определена параметрическим уравнением прямой в пространстве x = — 2 y = 1 + 2 · λ z = 4 — 3 · λ , прямая b при помощи канонического уравнения прямой в пространстве x 1 = y — 1 — 2 = z + 4 6 . Найти расстояние между скрещивающимися прямыми.
Понятно, что прямая а пересекает точку M 1 ( — 2 , 1 , 4 ) с направляющим вектором a → = ( 0 , 2 , — 3 ) , а прямая b пересекает точку M 2 ( 0 , 1 , — 4 ) с направляющим вектором b → = ( 1 , — 2 , 6 ) .
Для начала следует произвести вычисление направляющих векторов a → = ( 0 , 2 , — 3 ) и b → = ( 1 , — 2 , 6 ) по формуле. Тогда получаем, что
a → × b → = i → j → k → 0 2 — 3 1 — 2 6 = 6 · i → — 3 · j → — 2 · k →
Отсюда получаем, что n → = a → × b → — это вектор плоскости χ , который проходит через прямую b параллельно a с координатами 6 , — 3 , — 2 . Получим:
6 · ( x — 0 ) — 3 · ( y — 1 ) — 2 · ( z — ( — 4 ) ) = 0 ⇔ 6 x — 3 y — 2 z — 5 = 0
Находим нормирующий множитель для общего уравнения плоскости 6 x — 3 y — 2 z — 5 = 0 . Вычислим по формуле 1 6 2 + — 3 2 + — 2 2 = 1 7 . Значит, нормальное уравнение примет вид 6 7 x — 3 7 y — 2 7 z — 5 7 = 0 .
Необходимо воспользоваться формулой, чтобы найти расстояние от точки M 1 — 2 , 1 , 4 до плоскости, заданной уравнением 6 7 x — 3 7 y — 2 7 z — 5 7 = 0 . Получаем, что
M 1 H 1 = 6 7 · ( — 2 ) — 3 7 · 1 — 2 7 · 4 — 5 7 = — 28 7 = 4
Отсюда следует, что искомым расстоянием является расстояние между заданными скрещивающимися прямыми, является значение 4 .
http://spravochnick.ru/matematika/rasstoyanie_mezhdu_skreschivayuschimisya_pryamymi_formula/
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/rasstojanie-mezhdu-skreschivajuschimisja-prjamymi/