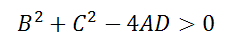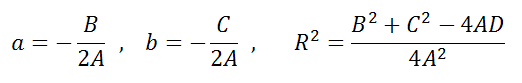Расстояние на координатной плоскости уравнение окружности

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

| A1A2| 2 = = ( x2 – x1) 2 + ( y2 – y1) 2 .

(1)

что и требовалось доказать.

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Планиметрия. Страница 6

1 2 3 4 5 6 7 8 9 10 11 12

1.Декартова система координат

Раздел геометрии, в котором геометрические фигуры и их свойства исследуются с помощью алгебры, называется аналитической геометрией. В основе этого метода лежит метод координат, который впервые был применен французским ученым Рене Декартом. Согласно этому методу любой геометрической фигуре или кривой на плоскости можно сопоставить некоторое математическое уравнение, которое связывает координаты данной фигуры или кривой.

(Рене Декарт (1596-1650) — французский философ, математик, физик, физиолог. В своих научных работах заложил основы аналитической геометрии и дал понятие переменной величины и функции, ввел также многие математические обозначения. Сформулировал закон сохранения количества движения и дал понятие импульса силы.)

Проведем на плоскости две взаимно перпендикулярные прямы x и y, пересекающиеся в точке О. Данные прямые называются осями координат. Прямая х — называется осью абсцисс и обозначается Ох, а прямая y — осью ординат и обозначается Оy. Точка О называется началом координат для обоих осей Ох и Оy. На оси Ох вправо откладываются положительные значения, а влево — отрицательные. По оси Оy вверх откладываются положительные значения, а вниз — отрицательные. (Рис.1)

Рис.1 Декартова система координат.

Вся плоскость делится осями координат Ox и Oy на четыре четверти I, II, III, IV. Любую точку на плоскости можно задать двумя числами (координатами). Например, точка А имеет координаты (3,4). Она будет находится в I четверти, т.к. обе координаты у нее положительны. Точка В имеет координаты (-4,-2) и она будет находится в III четверти, т.к. обе координаты у нее отрицательны. Во II и IV четвертях координаты точек будут иметь, соответственно, разные знаки.
Введенные на плоскости кординаты x и y называются декартовыми, которые названы так в честь французского ученого Рене Декарта.

2.Расстояние между точками

Пусть на плоскости в прямоугольной системе координат заданы две точки А(x1;y1) и B(x2;y2). (Рис.2) Проведем через точки А и В прямые, перпендикулярные осям координат. Точка С будет являться точкой пересечения этих прямых. Тогда в полученном прямоугольном треугольнике АВС расстояние между точками А и В можно найти по теореме Пифагора как

АВ 2 = АС 2 + ВС 2 .

или в координатной форме:

d 2 = (x2 — x1) 2 + (y2 — y1) 2 .

где d — расстояние между точками А и В.

Данная формула остается верной при условии,
что x1 = x2, y1 = y2
или x1 = x2, y1 ≠ y2
или x1 ≠ x2, y1 = y2

Рис.2 Расстояние между точками.

3.Уравнение окружности

Пусть дана окружность радиуса R и центром в точке О(x0;y0). Найдем уравнение окружности. (Рис.3). Любая точка, лежащая на окружности, равноудалена от центра окружности. Используя формулу расстояния между двумя точками, получим:

Т.е. координаты любой точки, лежащей на окружности, удовлетворяют последнему уравнению.

Если центр окружности лежит в начале координат,
т.е. x0 = y0 = 0, то уравнение имеет следующий вид:

Рис.3 Уравнение окружности.

4.Уравнение прямой

Пусть в прямоугольной системе координат задана прямая, которая пересекает ось y в точке В(0;b) и образует с осью Ох угол α (Рис.4). Если взять на прямой произвольную очку М(x,y) то тангенс угла наклона прямой с осью Ох можно найти из прямоугольного треугольника АВМ.

Уравнение остается справедливым и в случае, если угол α больше 90 градусов.

Рис.4 Уравнение прямой.

5.Координаты точки пересечения

Пусть даны две прямые a и b. Тогда, если они не параллельны, то они пересекаются в одной точке M. Следовательно, координаты точки пересечения должны удовлетворять обоим уравнениям прямых. (рис.5)

Рис.5 Координаты точки пересечения.

Репетитор: Васильев Алексей Александрович

Предметы: математика, физика, информатика, экономика, программирование.

2000 руб / 120 мин — подготовка к ЕГЭ и ГИА для школьников. 3000 руб / 120 мин — индивидуально (базовый уровень). 2000 руб / 120 мин — студенты.

Тел. 8 916 461-50-69, email: alexey-it@ya.ru

6.Пример 1

Докажите, что четырехугольник АВСD с вершинами в точках А (-4;-4), В (-5;4), С (4;2), D (5;-6) является параллелограммом. Найдите точку пересечения его диагоналей. (Рис.6)

Доказательство:

Согласно свойству параллелограмма, у него диагонали пересекаются в точке, которая делит их пополам. Следовательно, необходимо найти середины отрезков АС и BD. Если середины этих отрезков совпадут, то точки ABCD образуют параллелограмм.

Найдем середину отрезка АС — точку О (х;y):

х = (4-4)/2 = 0, y = (2 — 4)/2 = -1

Теперь найдем середину отрезка BD — точку О₁ (х₁;y₁):

Отсюда можно сделать вывод, что точки ABCD образуют параллелограмм. А точка О (0;-1) является точкой пересечения его диагоналей.

Рис.6 Задача. Докажите, что четырехугольник АВСD.

Пример 2

Докажите, что точки А (-3;-2), В (1;1), С (3;2,5) лежат на одной прямой. Какая из них лежит между двумя другими.(Рис.7)

Решение:

Составим уравнение прямой, проходящей через точки А и В. Пусть прямая проходит через точки А и В. Тогда:

-2 = -3*k + b прямая проходит через точку А.

1 = k + b прямая проходит через точку В.

Из первого уравнения b = 3*k — 2 подставим во второе:

1 = k + 3*k — 2 или 3 = 4*k

Отсюда, k = 3/4, b = 1/4

Отсюда следует, что уравнение прямой, проходящей через точку А и В имеет вид:

Проверим, удовлетворяет ли этому уравнению точка С (3;2,5):

2,5 = 3 * 3/4 + 1/4 или 10/4 = 10/4

Следовательно, все три точки А,В и С лежат на одной прямой. А так как x_A Рис.7 Задача. Докажите, что точки А (-3;-2), В (1;1), С (3;2,5).

Пример 3

Найдите на оси х точку, равноудаленную от точек А (3;3) и В (-4;-4).

Решение:

Пусть эта точка С, лежащая на оси х с координатами (х;0). Тогда, так как расстояние от точек А и В равны, то можно составить следующее соотношение:

(х — 3) 2 + (0 — 3) 2 = (х + 4) 2 + (0 + 4) 2

x 2 — 6 x + 9 + 9 = x 2 + 8 x + 16 + 16

Следовательно, координаты точки С (-1;0)

Действительно, если опустить перпендикуляры от точек А и В на ось х (Рис.8), то прямоугольные треугольники ADF и BCD равны, так как их катеты имеют одинаковые длины 3 и 4 ед. А следовательно, и равны гипотенузы.

Рис.8 Задача. Найдите на оси х точку.

Пример 4

Даны точки А (-4;-1) и В (3;3). Составьте уравнение окружности, диаметром которой является отрезок АВ.

Решение:

Так как отрезок АВ является диаметром окружности, то можно найти координаты центра окружности, найдя середину отрезка АВ. Составим следующие соотношения:

Т.е. центр окружности находится в точке О (-1/2;1).

Теперь найдем R 2 , используя формулу расстояния между точками О (-1/2;1) и В (3;3):

R 2 = (3 + 1/2) 2 + (3 — 1) 2 = 65/4

Таким образом, уравнение окружности примет следующий вид:

(х + 1/2) 2 + (y — 1) 2 = 65/4 (Рис.9)

Рис.9 Задача. Даны точки А (-4;-1) и В (3;3).

Пример 5

При каких значениях с прямая x + y + c = 0 и окружность х 2 + y 2 = 1 пересекаются, касаются, не имеют общих точек.

Решение:

По условию задачи уравнение прямой имеет вид: x + y + c = 0. Следовательно, x = — y — c. Если окружность и прямая пересекаются, то они имеют общие точки. Поэтому мы можем подставить это выражение в уравнение окружности.

y 2 + 2cy + c 2 + y 2 = 1

2y 2 + 2cy + c 2 — 1 = 0

D = (2c) 2 — 4*2 (c 2 — 1) = 8 — 4c 2 ≥ 0

c 2 ≤ 2 или — ≤ c ≤

Отсюда можно сделать вывод :

а) если | c | > , то решений нет (т.е. точек пересечения);

б) если | c | = , то окружность и прямая имеют одну точку пересечения;

в) если | c | Рис.10 Задача. При каких значениях с.

Окружность на координатной плоскости

Окружность на плоскости — это множество точек на плоскости равноудаленных от точки центра. На рисунке данная точка обозначена C.

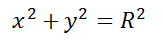
Окружность радиуса R с центром в точке C(a;b) представляется уравнением:

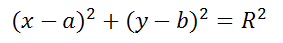
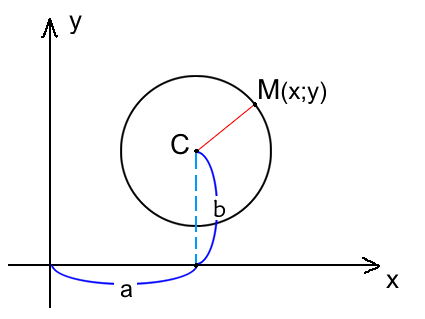
Расстояние от центра окружности С(a;b) до точки M(x;y) называется радиусом окружности R (на рисунке красная линия ).
Это уравнение можно записать в виде: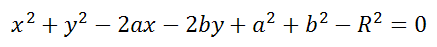

Если уравнение помножить на любое число A, то получим

Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.

Необходимые условия для этого:
1. Отсутствие в уравнение второй степени члена с произведением xy;
2. Коэффициенты при x 2 и y 2 были равны в уравнение вида: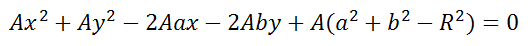

3. Если выполняется неравенство

Как найти радиус и центр окружности

Уравнение Ax 2 +Bx+Ay 2 +Cy+D=0 если оно удовлетворяет примечаниям (1, 2 и 3), то тогда (a;b) и радиус R окружности можно найти по формулам:

Пример 1
Уравнение 5x 2 -10x+5y 2 +20y-20=0
Здесь
A=5, B=-10, C=20, D=-20
Оно удовлетворяет примечаниям 1, 2 и выполняется неравенство

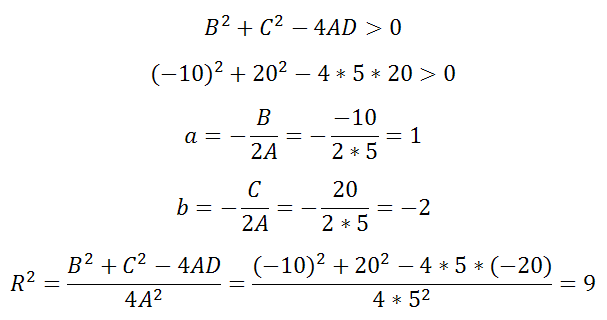
Решая, получаем что центр есть (1;-2), а радиус R=3

Анимационный график окружности

Пример 2
Уравнение второй степени x 2 +4xy+y 2 =1 не является окружностью, так как в нём есть член 4xy.

Пример 3
Уравнение второй степени 4x 2 +9y 2 =36 не представляет окружность, так как в нём коэффициенты при x 2 и y 2 не равны.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 3.8 / 5. Количество оценок: 6