Онлайн калькулятор. Расстояние от точки до прямой на плоскости
Предлагаю вам воспользоваться онлайн калькулятором для вычисления расстояния от точки до прямой.
Воспользовавшись онлайн калькулятором, вы получите детальное пощаговое решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление расстояния от точки до прямой на плоскости и закрепить пройденный материал.
Найти расстояние от точки до прямой на плоскости
Ввод данных в калькулятор для вычисления расстояния от точки до прямой на плоскости
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления расстояния от точки до прямой на плоскости
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория: Расстояние от точки до прямой на плоскости
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Если задано уравнение прямой на плоскости A x + B y + C = 0, то расстояние от точки M(M x , M y ) до прямой можно найти используя следующую формулу
| d = | |A·M x + B·M y + C| |
| √ A 2 + B 2 |
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Вычисление расстояния от точки до прямой
Этот калькулятор онлайн вычисляет расстояние от точки до прямой заданной в каноническом виде (для трехмерного случая):
Онлайн калькулятор для вычисления расстояния от точки до прямой не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: \( -\frac<2> <3>\)
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: \( -1\frac<5> <7>\)
Расстояние от точки до прямой онлайн
С помощю этого онлайн калькулятора можно найти расстояние от точки до прямой. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до прямой, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние от точки до прямой − теория, примеры и решения
Рассмотрим эту задачу в двухмерном и трехмерном пространствах.
1. Расстояние от точки до прямой на плоскости
Пусть в двухмерном пространстве задана точка M0(x0, y0) и прямая L:
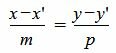 , , | (1) |
где q=(m,p) направляющий вектор прямой L.
Найдем расстояние от точки M0 до прямой (1)(Рис.1).
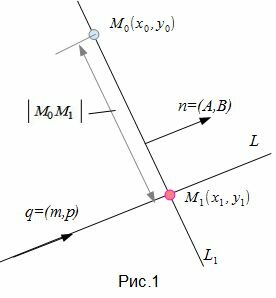 |
Алгоритм нахождения расстояния от точки M0 до прямой L содержит следующие шаги:
- построить прямую L1, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение прямых L и L1(точка M1)
- найти найти расстояние между точками M0 и M1.
Уравнение прямой, проходящей через точку M0(x0, y0) имеет следующий вид:
| A(x−x0)+B(y−y0)=0 | (2) |
Как видно из рисунка Рис.1, для того, чтобы прямая L1 была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L1, поэтому в качестве нормального вектора прямой L1 достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L1, представленной уравнением (2) можно записать так:
| m(x−x0)+p(y−y0)=0 | (3) |
| mx+py−mx0−py0=0 | (4) |
Для нахождения точки пересечения прямых L и L1, которая и будет проекцией точки M0 на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M1(x1, y1).
Найдем точку пересечения прямых L и L1 другим методом.
Выведем параметрическое уравнение прямой (1):
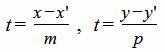 |
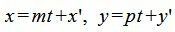 | (5) |
Подставим значения x и y в (4):
| m(mt+x’)+p(pt+y’)−mx0−py0=0 |
| m 2 t+mx’+p 2 t+py’−mx0−py0=0 |
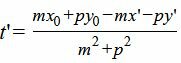 | (6) |
Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L1(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M0 на прямую L:
Далее находим расстояние между точками M0 и M1 используя формулу:
 . . | (7) |
Пример 1. Найти расстояние от точки M0(−6, 2) до прямой
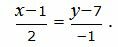 | (8) |
Направляющий вектор прямой (8) имеет вид:
Т.е. m=2, p=−1. Из уравнения прямой (8) видно, что она проходит через точку M’ (x’, y’)=(1, 7)(в этом легко убедится − подставляя эти значения в (8) получим тождество 0=0), т.е. x’=1, y’=7. Подставим значения m, p, x0, y0, x’, y’ в (6):
 |
 |
 , , |
Подставляя значение t в (5), получим:
 |
Вычислим расстояние между точками M0(-6, 2) и M1
 |
Упростим и решим:
  |
Расстояние от точки M0(-6, 2) до прямой (8) :
 |
2. Расстояние от точки до прямой в пространстве
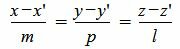 , , | (9) |
где q=(m, p, l) направляющий вектор прямой L.
Найдем расстояние от точки M0 до прямой (9)(Рис.2).
 |
Алгоритм нахождения расстояния от точки до прямой L содержит следующие шаги:
- построить плоскость α, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение плоскости α и прямой L(точка M1)
- найти расстояние между точками M0 и M1.
| A(x−x0)+B(y−y0)+C(z−z0)=0 | (10) |
где n=(A,B,C) нормальный вектор плоскости α.
Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (10) можно записать так:
| m(x−x0)+p(y−y0)+l(z−z0)=0 |
| mx+py+lz−mx0−py0−lz0=0 | (11) |
Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M0 на прямую L, выведем параметрическое уравнение прямой (9):
 |
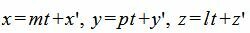 | (12) |
Подставим значения x и y в (11):
| m(mt+x’)+p(pt+y’)+l(lt+z’)−mx0−py0−lz0=0 |
| m 2 t+mx’+p 2 t+py’+l 2 t+ly’−mx0−py0−lz0=0 |
 | (13) |
Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (11). Следовательно, подставляя значение t’ в (12) получим координаты проекции точки M0 на прямую L:
| M1(x1, y1, , z1), |
Далее вычисляем расстояние между точками M0 и M1 используя формулу
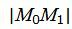 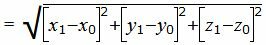 , , | (14) |
которое является расстоянием между точкой M0 и прямой (9).
Пример 2. Найти расстояние от точки M0(1, 2, 1) до прямой
 | (15) |
Направляющий вектор прямой (15) имеет вид:
Т.е. m=2, p=4, l=−6. Из уравнения прямой (15) видно, что она проходит через точку M’ (x’, y’, z’)=(4, 3, 1)(в этом легко убедится − подставляя эти значения в (15) получим тождество 0=0=0), т.е. x’=4, y’=3, z’=1. Подставим значения m, p, l x0, y0, z0 x’, y’, z’ в (13):
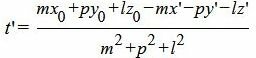 |
 |
 |
Подставляя значение t=t’ в (12), получим координаты точки M1:
 , , |
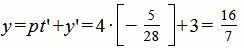 , , |
 . . |
Далее, используя формулу (14) вычисляем расстояние от точки M0 до прямой (15):
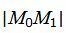 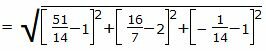 . . |
Упростим и решим:
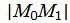   . . |
Расстояние от точки M0(1, 2, 1) до прямой (15) :
http://www.math-solution.ru/math-task/lp-dist-point-line
http://matworld.ru/analytic-geometry/rasstojanie-tochka-prjamaja.php