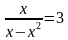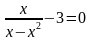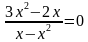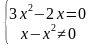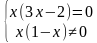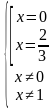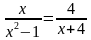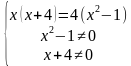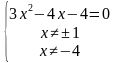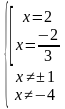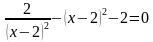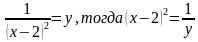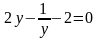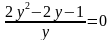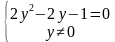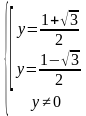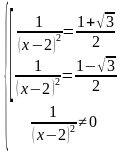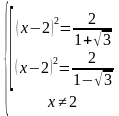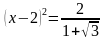«Решение неравенств». 10-й класс
Разделы: Математика
Класс: 10
Цели:
- Систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением методов решения рациональных неравенств.
- Содействовать развитию математического мышления учащихся,умению комментировать,тренировать память.
- Воспитание ответственного отношения к учебному труду,чувства товарищества и взаимопомощи.
Оборудование: интерактивная доска, раздаточный материал(разноуровневые карточки с практическими заданиями).
Структура урока:
- Сообщение темы и цели урока (1 мин.)
- Проверка домашнего задания (5 мин.)
- Систематизация знаний и умений по пройденному материалу (10 мин.)
- Инструктирование по выполнению заданий в группах (3 мин.)
- Выполнение заданий в группах (15 мин.)
- Проверка и обсуждение полученных результатов (8 мин.)
- Постановка домашнего задания (2 мин.)
- Подведение итогов урока (1 мин.)
Ход урока
I. Сообщение темы и цели урока.
Сегодня на уроке мы будем решать неравенства методом интервалов и методом замены переменных. Эпиграфом к сегодняшнему уроку будут слова Ньютона:“При изучении наукпримеры не менее поучительны,нежели правила” и слова Ломоносова: “Примеры учат больше,чем теория”.
II. Проверка домашнего задания.
На дом были даны неравенства. Проверьте ваше решение по интерактивной доске.
Отметим на числовой оси корни числителя и знаменателя.
Ответ: 
≥
Преобразуем исходное неравенство
–
≥ 0



Применим метод интервалов.
III. Систематизация знаний и умений по пройденному материалу.
Решим методом интервалов следующее неравенство. (Учитель на доске дает образец решения неравенств).
≥ 0
Рассмотрим функцию
1. Область определения функции f(x)находим из системы неравенств
Область определения: [-4; 3) U (3; 4]
2. Уравнение f (x) ═ 0 имеет корни: -4; 4; 3,5
Ответ: [-4; 3) U [3,5; 4]
Следующее неравенство решим методом замены переменных.
(
)² + 7 (
) +12 0
≤ 0
≥ 0
V. Выполнение заданий в группах.
VI. Проверка и обсуждение полученных результатов.
Проверьте по интерактивной доске решение работы.
Учащиеся осуществляют самопроверку и самооценку заданий. Получают разъяснения по возникающим при этом вопросам.
Ответы к рассмотренному варианту.
Воспользуемся методом интервалов, получим :
≤ 0
Замена
Тогда t-1 — 
Урок в 10 классе «Рациональные уравнения».
методическая разработка по алгебре (10 класс) по теме
Данный урок предназначен для изучения темы в 10 классе: «Рациональные уравнения.» Тип урока: урок- лекция.
Скачать:
| Вложение | Размер |
|---|---|
| Данный урок предназначен для изучения темы в 10 классе: «Рациональные уравнения.» Тип урока: урок- лекция. | 166 КБ |
| 10 класс: «Рациональные уравнения.» | 209.5 КБ |
Предварительный просмотр:
МОУ «Гимназия № 5 г. Белгорода»
Тема урока: Рациональные уравнения.
УМК : Алгебра и начала анализа: учеб. Для 10кл. общеобразоват. учреждений/[С.М.Никольский, М.К. Потапов.].-5-е изд., доп.-М.: Просвещение , 2006.-432с. Стр.65-74., 45-47.
Образовательная: систематизировать и обобщить известные из основной школы сведения о рациональных выражениях; показать способы решения рациональных уравнений;
Развивающая: расширить и углубить изучение различных видов рациональных уравнений разнообразными методами.
Воспитывающая: показать значимость изучаемой темы в разделе математика.
Тип урока: урок- лекция.
- Постановка цели урока (1мин).
- Подготовка к изучению нового материала(2 мин).
- 3.Ознакомление с новым материалом(38мин).
- 4.Итог урока.(2 мин)
- 5.Домашнее задание (2 мин)
Оборудование урока: интерактивная доска, проектор, компьютер.
1. Рациональные выражения.
2. Рациональные уравнения.
3.Системы рациональных уравнений.
Алгебра возникла из решения практических задач с помощью уравнений. Цели алгебры оставались неизменными на протяжении тысячелетий- решались уравнения: сначала линейные, потом квадратные, а там и уравнения еще больших степеней. Но форма, в которой излагались алгебраические результаты, менялись до неузнаваемости.
Уравнение- это самая распространенная форма математической задачи. Учение об уравнениях является главным содержанием школьного курса алгебры. Для решения уравнений нужно уметь производить действия над одночленами, многочленами алгебраическими дробями, уметь производить разложение на множители, раскрывать скобки и т. д. Нужно привести свои знания в порядок. Мы начнем повторение с понятия «рациональные выражения». Сообщение ученика о рациональных выражениях известных из основной школы. Таким образом, учение об уравнениях невозможно без учения о законах действий.
II. Основная часть.
Главное в понятии уравнения – это постановка вопроса о его решении. Уравнение, левая и правая части которого есть рациональные выражения относительно х, называют рациональным уравнением с неизвестным х.
Например, уравнения 5х 6 — 9х 5 + 4х — Зх + 1 = 0, являются рациональными.
Корнем (или решением) уравнения с неизвестным х называют число, при подстановке которого в уравнение вместо х получается верное числовое равенство.
Решить уравнение — значит найти все его корни или показать, что их нет. При решении рациональных уравнений приходится умножать и делить обе части уравнения на не равное нулю число, переносить члены уравнения из одной части в другую, применять правила сложения и вычитания алгебраических дробей. В результате будет получаться уравнение, равносильное предшествующему, т. е. уравнение, имеющее те же корни, и только их.
Перечислим стандартные уравнения, которые были нами изучены. Ответы учащихся.( линейное уравнение , квадратное уравнение, простейшее степенное уравнение х n =а). Преобразование уравнений к одному из стандартных является основным шагом в решении уравнения. Полностью алгоритмизировать процесс преобразования нельзя, однако полезно запомнить некоторые приемы, общие для всех типов уравнений.
1).Уравнение вида А(х)•В(х) = О, где А(х) и В(х) — многочлены относительно х, называют распадающимся уравнением .
Множество всех корней распадающегося уравнения есть объединение множеств всех корней двух уравнений А(х)=0 и В(х)=0. К уравнениям вида А(х)=0 применяется метод разложения на множители. Суть этого метода : нужно решить уравнение А(х)=0, где А(х)=А 1 (х)А 2 (х)А 3 (х). Уравнение А(х)=0 заменяют совокупностью простых уравнений: А 1 (х)=0,А 2 (х)=0,А 3 (х)=0. Находят корни уравнений этой совокупности и делают проверку. Метод разложения на множители используется в основном для рациональных и тригонометрических уравнений.
Решим уравнение (х 2 — 5х + 6) (х 2 + х — 2) = 0.
Уравнение распадается на два уравнения.
х 2 — 5х + 6 = 0 х 1 = 2 и х 2 = 3
х 2 + х — 2 = 0. х 3 = -2 и х 4 = 1
Значит, уравнение исходное имеет корни х 1 = 2, х 2 = 3, х 3 = -2, х 4 =1.
ПРИМЕР. Решим уравнение х 3 -7х+6=0.
х-1=0 , х 1 =1; х 2 +х-6=0, х 2 =2,х 3 =-3.
2).Уравнение вида , где А(х) и В(х) — многочлены относительно х.
Сначала решим уравнение
х 2 + 4х — 21 = 0. х 1 = 3 и х 2 = -7
Подставив эти числа в знаменатель левой части исходного уравнения, получим
х 1 2 — х 1 -6 = 9-3-6 = 0,
х 2 2 — х 2 — 6 = 49 + 7 — 6 = 50 ≠0.
Это показывает, что число х 1 = 3 не является корнем исходного уравнения, а число х 2 =- 7 — корень этого уравнения.
где А(х), В(х), С(х) и D(х) — многочлены относительно х, обычно решают по следующему правилу.
Решают уравнение А(х)•D(х) — С(х)·В(х) = 0 и отбирают из его корней те, которые не обращают в нуль знаменатель уравнения.
х 2 — 5х + 6 — (2х + 3) (х — 3) = 0.
х 1 = -5 и х 2 = 3.
Число х 1 не обращает в нуль знаменатель х — 3, а число х 2 обращает. Следовательно, уравнение имеет единственный корень = -5.
Найти корни рационального уравнения часто помогает замена неизвестного. Умение удачно ввести новую переменную- важный элемент математической культуры. Удачный выбор новой переменной делает структуру уравнения более прозрачной.
Решим уравнение х 8 + 4х 6 -10х 4 + 4х 2 + 1 = 0.
Число х 0 = 0 не является корнем уравнения, поэтому уравнение равносильно уравнению
х 4 + 4х 2 — 10 + + =0
Обозначим t = ,тогда х 4 + =t 2 -2 ,
получаем t 2 + 4t — 12 = 0, х 1 = 2 и х 2 = -6.
Следовательно, корни уравнения найдем, объединив все корни двух уравнений: =2, и =-6,
Первое уравнение имеет два корня -1 и 1, а второе уравнение не имеет действительных корней, поэтому уравнение имеет только два корня: -1 и 1. Ответ. -1; 1.
4). Симметрические уравнения.
Многочлен от нескольких переменных называют симметрическим многочленом, если его вид не изменяется при любой перестановке этих переменных.
Например, многочлены х + у, а 2 + b 2 — 1, zt и 5а 3 + 6ab + 5b 3 — симметрические многочлены от двух переменных, а многочлены х + у + г, а 3 + b 3 + с 3 , — симметрические многочлены от трех переменных.
В то же время многочлены х — у, а 2 –b 2 и а 3 + аb – b 3 — не симметрические многочлены.
Уравнение ax 4 +bx 3 +cx 2 +bx+a=0, где а R/ ,b R, с R называется симметрическим уравнением четвертой степени. Чтобы решить это уравнение необходимо:
1).Поделить обе части уравнения на х 2 и сгруппировать полученные выражения: .
2).Введение переменной уравнение приводится к квадратному.
Решите уравнение х 4 +5х 3 +4х 2 -5х+1=0.
Число 0 не является корнем уравнения. Поделим обе части уравнения на х 2 ≠0.
Системы рациональных уравнений.
Системы уравнений появляются при решении задач, в которых неизвестными являются несколько величин. Эти величины связаны определенной зависимостью, которые записываются в виде уравнений.
Уравнение, левая и правая части которого есть рациональные выражения относительно х и у, называют рациональным уравнением с двумя неизвестными х и у.
Если надо найти все пары чисел х и у, каждая из которых является решением каждого из данных уравнений с двумя неизвестными х и у, то говорят, что надо решить систему уравнений с двумя неизвестными х и у и каждую такую пару называют решением этой системы.
Неизвестные могут обозначаться и другими буквами. Аналогично определяется система уравнений, число неизвестных в которой больше двух.
Если каждое решение первой системы уравнений является решением второй системы, а каждое решение второй системы уравнений является решением первой системы, то такие системы называют равносильными. В частности, равносильными считаются две системы, не имеющие решений.
Например, равносильны системы
1). Способ подстановки .
ПРИМЕР 1. Решим систему уравнений
Выразив у через х из первого уравнения системы, получим уравнение:
Решив уравнение 5x 2 -4(3x-1)+3(3x-1) 2 =9, найдем его корни х 1 = 1 и х 2 = . Подставив найденные числа х 1 и х 2 в уравнение у = 3х — 1 , получим у 1 = 2
и у = Следовательно, система имеет два решения: (1; 2) и ( ; )
2). Метод алгебраического сложения.
ПРИМЕР 2. Решим систему уравнений
Оставив без изменения первое уравнение системы и сложив первое уравнение со вторым, получим систему равносильную системе.
Все решения системы есть объединение всех решений двух систем:
Решив каждую из этих систем, найдем все решения системы :
3). Метод введение новых неизвестных.
ПРИМЕР 3. Решим систему уравнений
Обозначив u = ху, v = х — у, перепишем систему в виде
Найдем ее решения: u 1 = 1, v 1 = 0 и u 2 = 5, v 2 = 4. Следовательно, все решения системы есть объединение всех решений двух систем:
Решив методом подстановки каждую из этих систем, найдем ее решения системы: (1; 1), (-1; -1), (5; 1), (-1; -5).
Ответ. (1; 1), (-1; -1), (5; 1), (-1; -5).
4). Уравнение вида ах 2 + bху + су 2 = 0, где а, b, с — данные неравные нулю числа, называют однородным уравнением относительно неизвестных х и у.
Рассмотрим систему уравнений, в котором есть однородное уравнение.
ПРИМЕР 4. Решим систему уравнений
Обозначив t = , перепишем первое уравнение системы в виде t 2 +4t+3=0.
Уравнение имеет два корня t 1 = -1 и t 2 = -3, поэтому все решения системы есть объединение всех решений двух систем:
Решив каждую из этих систем, найдем все решения системы:
При решении некоторых систем помогает знание свойств симметрических многочленов.
Введем новые неизвестные α = х + у и β= ху, тогда, х 4 +у 4 = α 4 -4 α 2 β+2 β 2
Поэтому систему можно переписать в виде
Решим квадратное уравнение относительно β: β 1 =6, β 2 =44.
Следовательно, все решения системы являются объединением
всех решении двух систем:
Первая система имеет два решения х 1 = 2, у 1 = 3 и х 2 = 3, у 2 =2, а вторая система не имеет действительных решений. Следовательно, система имеет два решения: (х: 1 ; у 1 ) и (х 2 ;у 2 )
Сегодня мы подвели итоги изучения темы рациональные уравнения. Мы поговорили об общих идеях, общих методах, на которых основана вся школьная линия уравнений.
Выделили методы решения уравнений:
1) метод разложения на множители;
2) метод введения новых переменных.
Расширили представления о методах решения систем уравнений.
На следующих 4 уроках проведем практические занятия. Для этого необходимо выучить теоретический материал, и подобрать из учебника по 2 примера на рассмотренные методы решения уравнений и систем уравнений, на 6 уроке будет проведен семинар по этой теме, для этого необходимо подготовить вопросы: формула бинома Ньютона, решение симметрических уравнений 3,5 степени. Заключительный урок по этой теме — зачет.
- Алгебра и начала анализа: учеб. Для 10кл. общеобразоват. учреждений/[С.М.Никольский, М.К. Потапов.].-5-е изд., доп.-М.: Просвещение , 2006.-432с. Стр.65-74., 45-47.
- Математика: тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов/сост. Г.И.Ковалева, Т.И. Бузулина — Волгоград: Учитель,2009.-494с. – стр. 62-72,194-199.
- Титаренко А.М. Математика : т9-11 классы: 6000 задач и примеров/А.М. Титаренко.-М.:Эксмо,2007.-336с.
Много можно говорить об уравнениях. В этой области математики существуют вопросы, на которые математики еще не дали ответа. Возможно, кто-то из вас найдет ответы на эти вопросы.
Альберт Эйнштейн говорил: « Мне приходиться делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента. А уравнения будут существовать вечно ».
Уроки 2-5 отводиться практическим занятиям. Основным видом занятий на этих уроках является самостоятельная работа учащихся по закреплению и углублению теоретического материала, изложенного на лекции. На каждом из них проводится повторение вопросов теории и опрос учащихся. На основе самостоятельной работы на уроке и дома обеспечивается повторение и усвоение вопросов теории, ведется целенаправленная работа по выработке умений и навыков решения задач различного уровня сложности, проводится опрос учащихся. Цель: закрепить и углубить теоретический материал изложенный на лекции, научиться применять его на практике, усвоить алгоритмы решения типовых примеров и задач, добиться, чтобы все учащиеся усвоили основное содержание изучаемого раздела на уровне программных требований.
На семинар отводится 6-й и 7-й уроки, причем целесообразно на 6-м уроке провести семинар, а 7-м- зачет.
План урока – семинара.
Цель: повторение, углубление и обобщение пройденного материала, отработать основные методы, способы и приемы решения математических задач, приобретение новых знаний, обучение самостоятельному применению знаний в нестандартных ситуациях.
1. В начале урока организуется программный контроль. Цель проведения работы- проверка сформированности умений и навыков выполнения несложных упражнений. В процессе фронтального опроса учеников, неверно указавших номер ответа, учитель выясняет, какие из заданий вызвали затруднение. Далее ведется устная или письменная работа по устранению ошибок. На проведение программированного контроля отводится не более 10 минут.
2. Дифференцированный опрос нескольких учащихся по вопросам теории.
3. Историческая справка о возникновении и развитии понятия уравнения (сообщение ученика). Формула бином Ньютона. Решение симметрических уравнений третьей степени, четвертой степени, пятой степени.
х 4 -2х 3 -х 2 -2х+1=0
2х 4 +х 3 -11х 2 +х+2=0
х 5 -х 4 -3х 3 -3х 2 -х+1=0
2х 5 +3х 4 -5х 3 -5х 2 +3х+2=0
4. Решение примеров, проверка готовности учащихся к выполнению контрольной работы – это одна из главных задач семинара.
Проведение зачета не означает отказ от текущего контроля знаний учащихся. Оценки выставляются на практических и семинарских занятиях. На зачет выносятся некоторые типичные упражнения. Заранее ученикам сообщается, какой теоретический материал и упражнения будут представлены на зачете. Приведем содержание одной из карточек для проведения зачета по рассматриваемой теме.
Решите уравнения: (х+3) 4 +(х 2 +х-6) 2 =2(х-2) 4
Повторение. Рациональные уравнения и неравенства
Урок №10. СКАЧИВАЙТЕ файл на устройства, чтобы все знаки и формулы были видны и распознаны. Во время чтения файла онлайн происходит потеря формул.
Просмотр содержимого документа
«Повторение. Рациональные уравнения и неравенства»
Тема урока: Повторение. Рациональные уравнения и неравенства
Цели: обобщить и систематизировать знания учащихся по теме.
Откройте тетради и запишите сегодняшнее число и тему урока. Записываем решение только тех примеров, которые вызывают у вас затруднение при решении.
Пример 1. Решить уравнение:
Решение. Приведем данное уравнение к стандартному виду, перенеся 3 в левую часть:
Приведем к общему знаменателю, приведем подобные члены и получим уравнение:
Решение данного уравнения запишем через систему:
Вынесем за скобки общий множитель:
Получим следующее решение:
Учитывая ОДЗ, получим ответ: 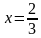
Пример 2. Решить уравнение:
Решение. Распишем данное уравнение, применяя основное свойство пропорции, и учтем ОДЗ:
В первом уравнении системы раскроем скобки, перенесем всё в левую часть, приведем подобные. Второе и третье задают ОДЗ, их тоже решим:

Решаем квадратное уравнение:
Оба корня подходят по ОДЗ.
Ответ: 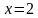
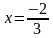
Пример 3. Решить уравнение:
Решение. Введем замену:
Получим уравнение относительно новой переменной следующего вида:
Приведем его к общему знаменателю:
Получили дробно-рациональное уравнение общего вида. Распишем его решение с помощью системы:
Решим квадратное уравнение, получим корни:
Вернемся к замене:
Применим свойство пропорции, получим:
Рассмотрим первое уравнение:
Правая часть больше 0, значит можем извлечь корень квадратный из обеих частей уравнения:
Тогда решением будет:
Рассмотрим второе уравнение:
Его правая часть меньше нуля, значит оно решений не имеет (квадрат не может быть отрицательным).
Пример 4. Решить неравенство
Решение. Найдем ОДЗ. В знаменателе корень четной степени, значит подкоренное выражение строго больше 0:
Так как знаменатель всегда положителен, перепишем неравенство в виде:
Применим формулу кубов к выражению и перепишем неравенство:
Вынесем общий множитель за скобку:
Решим данное неравенство методом интервалов, нанеся точки -1, 0, 1, и ОДЗ:
ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ
Домашнее задание: решить уравнение и неравенство
http://nsportal.ru/shkola/algebra/library/2013/03/03/urok-v-10-klasse-ratsionalnye-uravneniya
http://multiurok.ru/files/povtorenie-ratsionalnye-uravneniia-i-neravenstva.html






 ≥
≥ 
 –
–  ≥ 0
≥ 0 ≥ 0
≥ 0

 )² + 7 (
)² + 7 ( ) +12 0
) +12 0 ≤ 0
≤ 0 ≥ 0
≥ 0
 ≤ 0
≤ 0