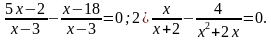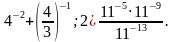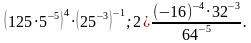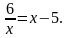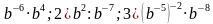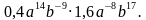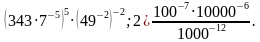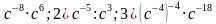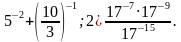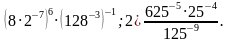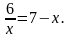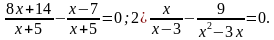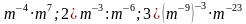Рациональные уравнения степень с целым показателем функция

Рациональные уравнения с примерами решения

Содержание:

Рациональные уравнения. Равносильные уравнения

два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.

Так, например, равносильными будут уравнения

Уравнения — не равносильны, так как корнем первого уравнения является число 10, а корнем второго — число 9.

Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.

1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;

2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;

3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.

Левая и правая части каждого из них являются рациональными выражениями.

Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.

В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения — дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.

Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.

Применение условия равенства дроби нулю

Напомним, что когда

Пример №202

Решите уравнение

Решение:

С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду где и — целые рациональные выражения. Имеем:

Окончательно получим уравнение:

Чтобы дробь равнялась нулю, нужно, чтобы числитель равнялся нулю, а знаменатель не равнялся нулю.

Тогда откуда При знаменатель Следовательно, — единственный корень уравнения.

Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:

Значит, решая дробное рациональное уравнение, можно:

1) с помощью тождественных преобразований привести уравнение к виду

2) приравнять числитель к нулю и решить полученное целое уравнение;

3) исключить из его корней те, при которых знаменатель равен нулю, и записать ответ.

Использование основного свойства пропорции

Если то где

Пример №203

Решите уравнение

Решение:

Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то Имеем: то есть ОДЗ переменной содержит все числа, кроме 1 и 2.

Сложив выражения в правой части уравнения, приведем его к виду: получив пропорцию:

По основному свойству пропорции имеем:

Решим это уравнение:

откуда

Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.

Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:

Таким образом, для решения дробного рационального уравнения можно:

1) найти область допустимых значений (ОДЗ) переменной в уравнении;

2) привести уравнение к виду

3) записать целое уравнение и решить его;

4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.

Метод умножения обеих частей уравнения на общий знаменатель дробей

Пример №204

Решите уравнение

Решение:

Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:

Областью допустимых значений переменной будут те значения при которых то есть все значения кроме чисел А простейшим общим знаменателем будет выражение

Умножим обе части уравнения на это выражение:

Получим: а после упрощения: то есть откуда или

Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.

Следовательно, число 12 — единственный корень уравнения. Ответ. 12.

Решая дробное рациональное уравнение, можно:

3) умножить обе части уравнения на этот общий знаменатель;

4) решить полученное целое уравнение;

5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.

Пример №205

Являются ли равносильными уравнения

Решение:

Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.

Первое уравнение имеет единственный корень а второе — два корня (решите уравнения самостоятельно). Следовательно, уравнения не являются равносильными.

Степень с целым показателем

Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:

где — натуральное число,

В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: кг. Как понимать смысл записи

Рассмотрим степени числа 3 с показателями — это соответственно

В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:

Число должно быть втрое меньше числа равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно, Равенство справедливо для любого основания при условии, что

Нулевая степень отличного от нуля числа а равна единице, то есть при

Вернемся к строке со степенями числа 3, где слева от числа записано число Это число втрое меньше, чем 1, то есть равно Следовательно, Рассуждая аналогично получаем: и т. д.

Приходим к следующему определению степени с целым отрицательным показателем:

если натуральное число, то

Контрольная работа № 3 по теме «Рациональные уравнения. Степень с целым отрицательным показателем. Функция y=k/x и её график» (8 класс, Мерзляк А.Г. и др.)

Даны четыре варианта контрольной работы, удобно вносить изменения и печатать.

Просмотр содержимого документа
«Контрольная работа № 3 по теме «Рациональные уравнения. Степень с целым отрицательным показателем. Функция y=k/x и её график» (8 класс, Мерзляк А.Г. и др.)»

Контрольная работа № 3 по теме «Рациональные уравнения. Степень с целым отрицательным показателем. Функция 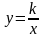и ее график»»

1. Решите уравнение:

1)

2. Запишите в стандартном виде число:

1) 324000; 2) 0,0042.

3. Представьте в виде степени с основанием а выражение:

1)

4. Упростите выражение

5. Найдите значение выражения:

1)

6. Преобразуйте выражение 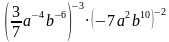так, чтобы оно не содержало степеней с отрицательными показателями.

1)

8. Решите графически уравнение

9. Порядок числа а равен –4, а порядок числа b равен 5. Каким может быть порядок значения выражения:

1. Решите уравнение:

1)

2. Запишите в стандартном виде число:

1) 275000; 2) 0,0028.

3. Представьте в виде степени с основанием b выражение:

1)

4. Упростите выражение

5. Найдите значение выражения:

1)

6. Преобразуйте выражение 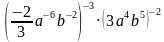так, чтобы оно не содержало степеней с отрицательными показателями.

1)

8. Решите графически уравнение

9. Порядок числа m равен –2, а порядок числа n равен 3. Каким может быть порядок значения выражения:

1. Решите уравнение:

1)

2. Запишите в стандартном виде число:

1) 419000; 2) 0,0051.

3. Представьте в виде степени с основанием c выражение:

1)

4. Упростите выражение

5. Найдите значение выражения:

1)

6. Преобразуйте выражение так, чтобы оно не содержало степеней с отрицательными показателями.

1)

8. Решите графически уравнение

9. Порядок числа b равен 6, а порядок числа c равен 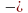5. Каким может быть порядок значения выражения:

1. Решите уравнение:

1)

2. Запишите в стандартном виде число:

1) 563000; 2) 0,0074.

3. Представьте в виде степени с основанием m выражение:

1)

4. Упростите выражение

5. Найдите значение выражения:

6. Преобразуйте выражение так, чтобы оно не содержало степеней с отрицательными показателями.

8. Решите графически уравнение

9. Порядок числа а равен 4, а порядок числа b равен –3. Каким может быть порядок значения выражения:

ГДЗ дидактические материалы по алгебре 8 класс Мерзляк, Полонский, Рабинович Вентана-Граф Задание: Вариант 2

1. Решите уравнение:

2. Запишите в стандартном виде число:

3. Представьте в виде степени с основанием a выражение:

4. Упростите выражение 0,2a^8b^(-10)*1,7a^(-6)b^12.

5. Найдите значение выражения:

6. Преобразуйте выражение (-2/3a^(-4)b^(-8))^(-2)*(3a^2b^12)^(-3) так, чтобы оно не содержало степеней с отрицательными показателями.

7. Вычислите:

8. Решите графически уравнение 6/x=5-x.

9. Порядок числа x равен -3, а порядок числа y равен 2. Каким может быть порядок значения выражения: