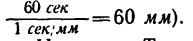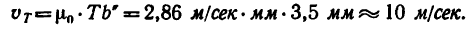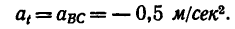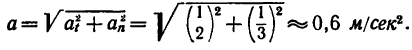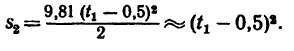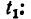Равнопеременное прямолинейное движение
Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
Проекция вектора скорости на ось ОХ:
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
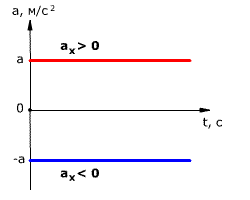
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
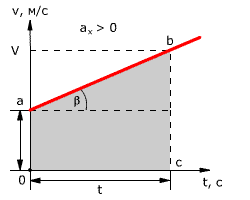
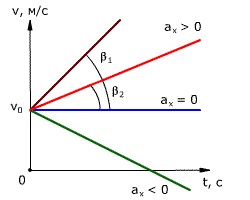
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
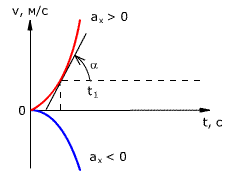
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx
Равнопеременное движение точки в теоретической механике
Равнопеременное движение точки:
Если
Если же постоянным остается только числовое значение касательного уравнения
то 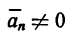
При 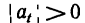
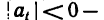
Уравнение равнопеременного движения независимо от его траектории имеет вид (см. § 63 в учебнике Е. М. Никитина)
Здесь 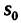
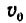
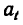
Числовое значение скорости точки в любой момент времени определяется из уравнения
Уравнения (1) и (2) являются основными формулами равнопеременного движения и они содержат шесть различных величин: три постоянные: 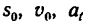
Следовательно, для решения задачи на равнопеременное движение точки в ее условии должно быть дано не менее четырех величин (систему двух уравнений можно решить лишь в том случае, если они содержат два неизвестных).
Если неизвестные входят в оба основных уравнения, например, неизвестны 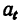
после исключения 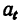

после исключения t из (1) и (2) 
В частном случае, когда начальные величины 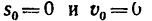
Уравнения (5) и (6) являются основными, а уравнения (7) и (8) — вспомогательными.
Равноускоренное движение из состояния покоя, происходящее под действием только силы тяжести, называется свободным падением. К этому движению применимы формулы (5) —(8), причем
Задача №1
Шарик, размерами которого можно пренебречь, начинает скатываться по наклонной плоскости из состояния покоя. Через 20 сек после начала движения шарик находится от исходного положения на расстоянии 6 м.
Определить ускорение шарика и его скорость в конце 10-й и 20-й сек, а также расстояние, пройденное шариком за первые 10 шс.
1. Из условия задачи следует, что 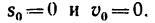
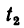
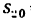
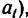
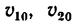
2. Найдем из формулы (7) скорость шарика, которую он приобретает в конце 20-й сек:
3. Найдем из формулы (6) ускорение шарика, которое он имеет, двигаясь по наклонной плоскости:
4. Теперь из этой же формулы (6) можно найти скорость в конце
10-й сек
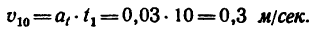
5. Из формулы (5) находим расстояние, пройденное точкой за первые 10 сек: 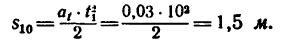
Задачу можно решить в ином порядке. Сначала из формулы (5) определить ускорение
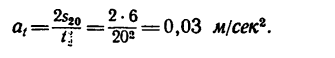
Затем из формулы (6) определить 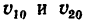
Задача №2
Автомобиль, движущийся равномерно и прямолинейно со скоростью 60 км/ч, увеличивает в течение 20 сек скорость до 90 км/ч. Определить, какое ускорение получит автомобиль и какое расстояние он проедет за это время, считая движение рарноускоренным.
1. Здесь также четыре данных величины:
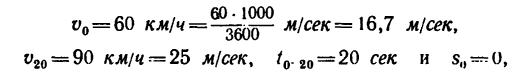
так как движение автомобиля рассматривается только на том участке траектории (дороги), где он движется с ускорением.
2. Из вспомогательной формулы (3), полагая в ней 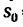
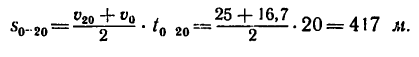
3. Из формулы (2) найдем ускорение, полученное автомобилем:
Задачу можно решить несколько иным путем. Сначала из формулы (2) найти ускорение автомобиля, а затем из формулы (1) найти пройденное расстояние.
Задача №3
Имея скорость 20 м/сек, автомобиль въезжает на криволинейный участок дороги, имеющий радиус закругления 200 м. За 40 сек равнопеременного движения он проезжает расстояние 400 м.
Определить, с каким касательным ускорением движется автомобиль, какова его скорость в конце пройденных 400 м и каково полное ускорение на середине этого пути.
1. Изобразим участок дороги, по которой движется автомобиль (рис. 197): О — начало участка, В— конец участка и А—его середина.
Для равнопеременного движения в задаче имеется четыре основных данных: 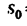
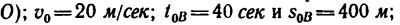
2. Из формулы (3) найдем скорость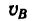
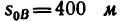
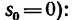
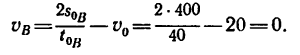
В конце рассматриваемого участка автомобиль останавливается, значит движение равнозамедленное *.
3. Найдем касательное ускорение автомобиля из формулы (2): 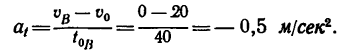
Получившееся отрицательное значение ускорения — подтверждение того, что движение автомобиля равнозамедленное.
4. Для того чтобы определить полное ускорение автомобиля в середине А участка ОВ, нужно сначала найти скорость 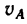
Эту скорость найдем из уравнения (4), приняв 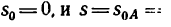
5. Находим нормальное ускорение автомобиля в точке А: 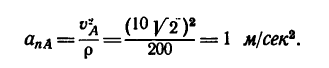
6. И, наконец, находим полное ускорение автомобиля:
Ускорение получается отрицательным, значит движение равнозамедленное. ** В дальнейшем для определения а„ нужно иметь значение
* Решение задачи можно начать с определения касательного ускорения из
формулы (I), считая 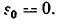
7. Вектор полного ускорения 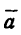
под углом 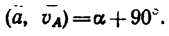
Задача №4
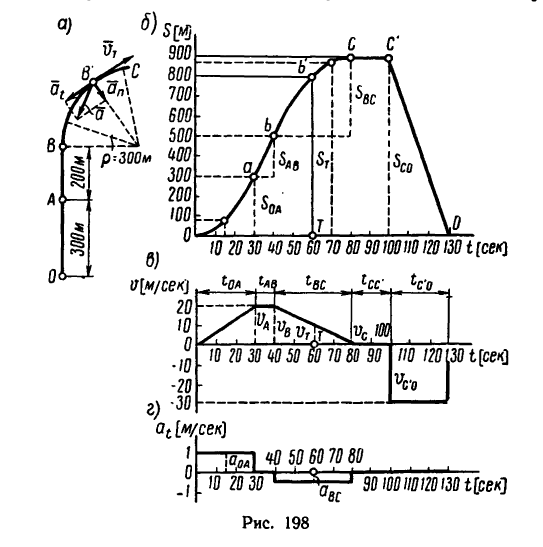
Точка движется в горизонтальной плоскости по заданной траектории ОАВС (рис. 198, а). Начав движение из состояния покоя, точка проходит участок ОА = 300 м равноускоренно за 30 сек, а расстояние от А до В, равное 200 м, она проходит
равномерно с той же скоростью, которую имеет в конце участка ОА. Из В точка движется в С уже равнозамедленно и проходит это расстояние за 40 сек. Остановившись в С, точка находится в покое 20 сек, а затем возвращается обратно в О по той же траектории, двигаясь равномерно и затратив на это движение 30 сек.
Построить графики перемещения, скорости и касательного ускорения точки.
Определить полное ускорение точки в момент времени через 60 сек после начала движения.
1. На уяастке О А, длина которого 300 м, точка движется равноускоренно из состояния покоя и проходит этот участок за 30 сек:
2. Находим ускорение 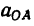
3. Скорость точки в конце участка О А находим из уравнения (6): 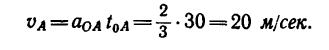
4. Следующий участок траектории АВ длиной 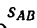
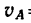
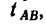
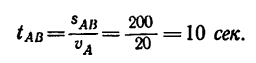
Причем в конце участка АВ скорость 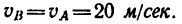
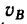
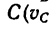
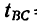
Длину участка ВС найдем по формуле (3), приняв
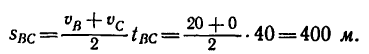
5. Ускорение аВс точки на участке ВС определяем из формулы (2): 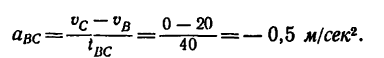
6.В конце траектории точка находится в покое в течение времени 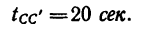
7. Затем точка движется обратно и проходит равномерно путь
за время
Скорость точки в этом движении
она направлена относительно скоростей первой части движения (например, относительно скоростей 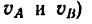
8. На все движение точки по траектории ОАВС в одну и другую сторону вместе с остановкой в конце траектории С 3атрачено 130 сек, которые складываются из времени:
= 30 сек — равноускоренного движения,
— равномерного движения,
— равнозамедленного движения,
— стояния точки,
— равномерного обратного движения.
9. Описанное выше движение точки изображаем графически, построив три графика: перемещений, скоростей и ускорений, расположенных один под другим (рис. 198, б, в, г).
Для построения графиков необходимо выбрать удобные масштабы для времени и остальных величин.
Рекомендуется графики, показанные на рис. 198, вычертить самостоятельно на отдельном листе бумаги в клетку. Масштабы по оси времени на всех трех графиках одинаковы. Масштаб времени / принят равным 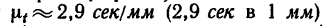
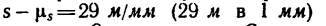
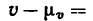
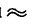
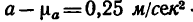

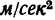
При самостоятельном построении этих графиков следует все масштабы увеличить, например принять 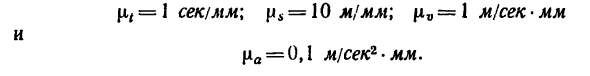
10. После построения графиков определяем ускорение точки в момент времени Т=60 сек после начала движения (см. условие задачи). Для этого прежде всего на графике перемещения из точки О (начало осей координат) по оси времени откладываем отрезок 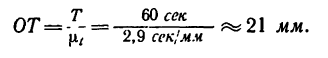
Этот отрезок определит на оси времени время Т = 60 сек (на самостоятельно построенном графике расстояние получится большим:
Из точки Т восставим перпендикуляр 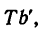
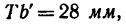
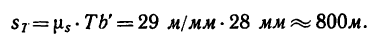
Если это расстояние отложить па траектории, то увидим, что точка в момент времени Т = 60 сек будет находиться на криволинейном участке траектории (положение 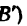
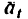
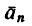
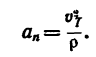
Скорость 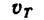
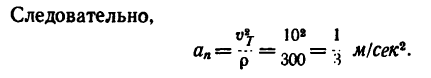
Касательное ускорение а, находим из графика ускорений
Полное ускорение движущейся точки в момент времени Т = 60 сек
Векторы 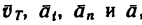
Задача №5
С крыши высотного дома через каждые 0,5 сек отрываются и свободно падают одна за другой капельки воды.
Определить, через сколько времени после отрыва первой капли расстояние между этой и следующей за ней каплей достигает 7,6 м?
1. Эта задача отличается от предыдущей тем, что в ней рассматривается движение не одной, а сразу двух материальных точек.
2. Изобразим перемещение обеих точек (рис. 199). Первая капля за искомое время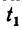
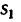
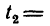
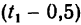
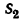
3. Расстояние 7,6 м между каплями через 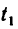

Используя формулу (5), получим уравнения падения капель: для первой капли:
для .второй капли
4. Подставив в уравнение (а) значения 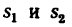
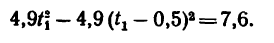
После раскрытия скобок и приведения подобных членов получим: 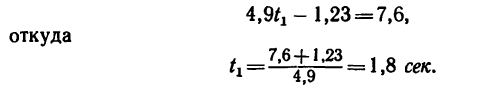
Таким образом, через 1,8 сек после отрыва первой капли или через 1,8-0,5 = 1,3 сек после отрыва второй расстояние между ними будет составлять 7,6 м.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Неравномерное движение точки по любой траектории
- Определение траектории, скорости и ускорения точки
- Кинематический способ определения радиуса кривизны траектории
- Равномерное вращательное движение
- Равновесие пространственной системы сходящихся сил
- Определение положения центра тяжести тела
- Равномерное прямолинейное движение точки
- Равномерное криволинейное движение точки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Прямолинейное равнопеременное движение
Прямолинейное равнопеременное движение — движение тела вдоль прямой, характеризующееся постоянным по модулю и направлению линейным ускорением.
Траектория такого движения — прямая, поэтому в задачах равнозначными являются понятия пути и модуля перемещения. Такое движение может быть описано несколькими соотношениями:
- вектор скорости тела при равнопеременном движении
- где
- — вектор конечной скорости движения
- — вектор начальной скорости движения
- — вектор ускорения
- — время движения
- вектор перемещения тела при равнопеременном движении
Однако это векторные уравнения, с которыми работать достаточно сложно, а иногда, просто не хочется. Попробуем, анализируя условия задачи, составить уравнения скалярного вида, спроецировав вектора на некую ось.
Рис. 1. Равноускоренное движение 1
Пример 1. Тело движется прямо с начальной скоростью и ускоряется. По задаче выставляем вектора на ось OX (движение прямолинейное) (рис. 1). Сказано, что тело движется вдоль оси (вектор направлен по оси) и ускоряется (вектор также направлен вдоль оси). Осталось зафиксированные вектора спроецировать:
- Для уравнения (1):
- Для уравнения (2):
В общем случае, мы не можем предугадать направления векторов и , соответственно, мы не можем указать точный знак проекции этих векторов на выбранную ось. Но не заморачиваемся: в результате решения задачи мы получим одно и то же по модулю число, даже если ошибёмся. Т.е. выбираем направления как хотим, а потом анализируем ответ.
Рис. 2. Равноускоренное движение-2
Пример 2. Тело движется в положительном направлении оси и затормаживает. По задаче тело движется вдоль оси (вектор направлен по оси), а торможение говорит о том, что вектор ускорения ( ) направлен против оси OX (рис. 2). Проецируем:
- Для уравнения (1):
- Для уравнения (2):
Рис. 3. Равноускоренное движение-3
Пример 3. Тело движется в отрицательном направлении оси и затормаживает. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а торможение говорит о том, что вектор ускорения ( ) направлен против движения, а значит, по оси OX (рис. 3). Проецируем:
- Для уравнения (1):
- Для уравнения (2):
Рис. 4. Равноускоренное движение-4
Пример 4. Тело движется в отрицательном направлении оси и ускоряется. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а ускорение говорит о том, что вектор ускорения ( ) направлен в сторону движения, а значит, против оси OX (рис. 4). Проецируем:
- Для уравнения (1):
- Для уравнения (2):
Вывод: только что мы получили восемь различных формул, применимых для решения задач. Очень не хотелось бы их помнить. К счастью, есть выход: запомнить и понять векторный вид этих уравнений (1) и (2), а далее, применительно к данной вам задаче, просто адаптировать их, используя проекции.
Кроме формул (1) и (2), имеется ещё одна расчётная формула, которая чаще всего используется, когда в задаче на нужно найти время или его не дано. Воспользуемся уже имеющимися (1) и (2), считая движение тела равноускоренным. Выделим из (1) время:
Подставим (3) в (2) при условии :
Таким образом, мы получили формулу, в которой нет параметра времени.
http://www.evkova.org/ravnoperemennoe-dvizhenie-tochki-v-teoreticheskoj-mehanike
http://www.abitur.by/fizika/teoreticheskie-osnovy-fiziki/mexanicheskoe-dvizhenie/pryamolinejnoe-ravnoperemennoe-dvizhenie/
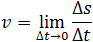
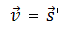

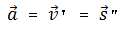

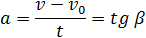
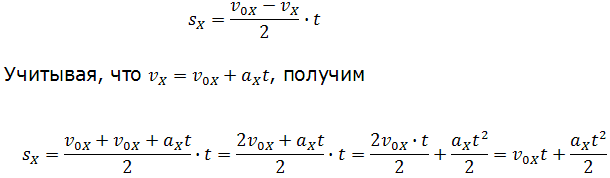
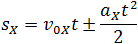
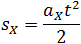
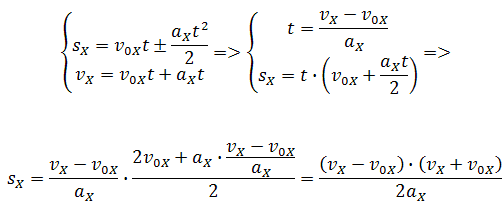
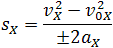
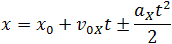
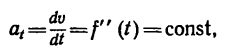




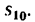
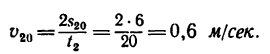
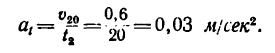
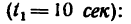
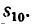
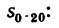
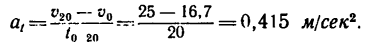
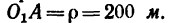
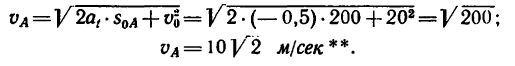
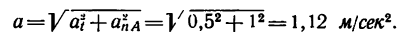
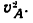
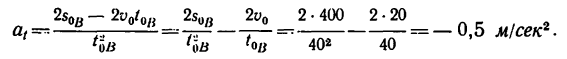
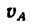
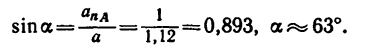
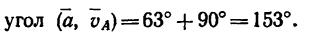
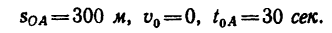
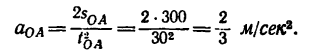
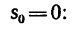
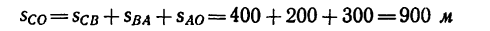
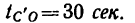
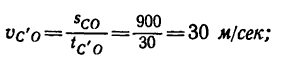
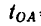 = 30 сек — равноускоренного движения,
= 30 сек — равноускоренного движения,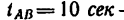 — равномерного движения,
— равномерного движения,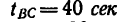 — равнозамедленного движения,
— равнозамедленного движения,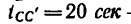 — стояния точки,
— стояния точки,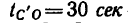 — равномерного обратного движения.
— равномерного обратного движения.