Равносильные переходы в решении уравнений и неравенств

Равносильные неравенства, преобразование неравенств

В процессе решения неравенств зачастую происходит переход от заданного неравенства к неравенствам иного вида, имеющим то же решение, но определяемое проще. Иными словами, в результате преобразований заданное неравенство возможно заменить равносильным ему, облегчающим поиск решения. Данная статья посвящена способам равносильных преобразований. Сформулируем определение, рассмотрим основные виды преобразований.

Равносильные неравенства: определение, примеры

Равносильные неравенства – неравенства, имеющие одни и те же решения. В частном случае, неравенства, не имеющие решений, тоже называются равносильными.

Иными словами, если неравенства равносильны и имеют решения, то любое решение первого будет являться и решением второго. Ни одно из равносильных неравенств не имеет решений, не являющихся решениями других, равносильных ему неравенств.

Даны три равносильных неравенства: x > 2 , 2 · x : 2 > 2 и x > 3 — 1 . В самом деле, множества решений этих неравенств одинаковые, решение каждого их них – числовой промежуток ( 2 , + ∞ ) .

Неравенства х 6 ≥ — 2 и | х + 7 | 0 являются равносильными, поскольку оба не имеют решений.

Неравенства х > 3 и х ≥ 3 – не равносильные: х = 3 служит решением второго из этих равенств, но не служит решением первого.

Отметим, что указанное определение относится к неравенствам как с одной переменной, так и с двумя, тремя и более.

Равносильные преобразования неравенств

Возможно совершить некоторые действия с правой и левой частью неравенств, что даст возможность получать новые неравенства, имеющие решения, как и у исходного.

Равносильное преобразование неравенства – это замена исходного неравенства равносильным ему, т.е. таким, которое имеет то же множество решений. Сами действия-преобразования, приводящие к равносильному неравенству, тоже называют равносильными преобразованиями.

Равносильные преобразования дают возможность находить решения неравенств, преобразуя заданное неравенство в равносильное ему, но более простое и удобное для решения.

Рассмотрим основные виды равносильных преобразований: по сути без них не обходится решение ни одного неравенства. Отметим также, что равносильные преобразования неравенств очень похожи на равносильные преобразования уравнений. Схожи и принципы доказательства, только, конечно, в данном случае доказательства будут строиться на основе свойств числовых неравенств.

Итак, перечислим основные виды равносильных преобразований неравенств:

1. Замена выражений в обоих частях неравенства тождественно равными выражениями на области допустимых значений (ОДЗ) переменных заданного неравенства есть равносильное преобразование неравенства.

Доказательство 1

Докажем утверждение. Пусть дано неравенство с одной переменной A ( x ) B ( x ) , где A ( x ) и B ( x ) — некие выражения с переменной x . Допустим, выражение C ( x ) является тождественно равным выражению A ( x ) , а выражение D ( x ) является тождественно равным B ( x ) на ОДЗ заданного неравенства. Найдем доказательство, что неравенство C ( x ) D ( x ) служит равносильным неравенству A ( x ) B ( x ) . С этой целью нам нужно продемонстрировать тот факт, что любое решение q заданного неравенства будет также решением неравенства C ( x ) D ( x ) , и наоборот: любое решение неравенства C ( x ) D ( x ) будет решением заданного неравенства A ( x ) B ( x ) .

Мы приняли, что q – решение неравенства A ( x ) B ( x ) , тогда верным будет числовое неравенство A ( q ) B ( q ) . Отсюда по разностному определению неравенства выводим, что A ( q ) − B ( q ) 0 .

Выражение A ( q ) − B ( q ) можно записать в виде A ( q ) + ( C ( q ) − C ( q ) ) − B ( q ) + ( D ( q ) − D ( q ) ) , что является тем же самым, ( A ( q ) − C ( q ) ) + C ( q ) − ( B ( q ) − D ( q ) ) − D ( q ) . Выражения A ( x ) и C ( x ) , B ( x ) и D ( x ) по условию тождественно равны, тогда: A ( q ) = C ( q ) и B ( q ) = D ( q ) , откуда A ( q ) − C ( q ) = 0 и B ( q ) − D ( q ) = 0 . Таким образом, ( A ( q ) − C ( q ) ) + C ( q ) − ( B ( q ) − D ( q ) ) − D ( q ) = 0 + C ( q ) − 0 − D ( q ) = C ( q ) − D ( q ) . Мы продемонстрировали, что значение выражения A ( q ) − B ( q ) равно значению выражения C ( q ) − D ( q ) , а поскольку A ( q ) − B ( q ) 0 , то и C ( q ) − D ( q ) 0 . Отсюда делаем вывод, что C ( q ) D ( q ) . И крайнее неравенство означает, что q – решение неравенства C ( x ) D ( x ) .

Таким же образом доказывается, что любое решение неравенства C ( x ) D ( x ) будет решением и неравенства A ( x ) B ( x ) , тем самым будет доказано и исходное утверждение.

Подобные преобразования не должны сужать ОДЗ заданного неравенства, тогда возможно совершать тождественные преобразования обеих сторон неравенства.

Покажем пример использования.

Рассмотрим неравенство x > 2 + 6 . В правой части возможно заменить сумму значением так, чтобы получилось равносильное неравенство x > 8 .

В неравенстве 3 · ( x + 1 ) − 2 · x + 11 ≤ 2 · y + 3 · ( y + 1 ) + x , в обоих его частях мы раскроем скобки и приведем подобные слагаемые, получив в итоге равносильное неравенство x + 14 ≤ 5 · y + 3 + x . Если детально разобрать наши действия, то мы заменили левую часть данного неравенства тождественно равным ей выражением x + 14 , а правую часть – тождественно равным ей выражением 5 · y + 3 + x на области допустимых значений переменных x и y заданного неравенства.

Еще раз особенно укажем, как важен учет ОДЗ (область допустимых значений) при совершении замены частей неравенства тождественными выражениями. В случае, когда ОДЗ нового неравенства будет отлична от ОДЗ исходного, неравенство не может считаться равносильным. Это крайне важный аспект, пренебрежение им приводит к неверным ответам при решении неравенств.

1. Прибавление или вычитание из обеих частей неравенства одного и того же числа является равносильным преобразованием.

Доказательство 2

Приведем обоснование указанного утверждения. Допустим, задано неравенство A ( x ) B ( x ) и некое число c . Необходимо доказать, что заданному равносильно неравенство A ( x ) + c B ( x ) + c , которое мы получим, прибавив к обеим частям исходного неравенства число c . Продемонстрируем, что любое решение q заданного неравенства будет также и решением неравенства A ( x ) + c B ( x ) + c , и наоборот.

Мы приняли, что q – решение неравенства A ( x ) B ( x ) , тогда верно следующее: A ( q ) B ( q ) . Из свойств числовых неравенств следует, что к обеим частям верного числового неравенства можно прибавить любое число. Мы прибавим число c к обеим частям крайнего неравенства, получим A ( q ) + c B ( q ) + c , и это означает, что q служит решением неравенства A ( x ) + c B ( x ) + c .

Подобным же образом можно доказать, что любое решение неравенства A ( x ) + c B ( x ) + c будет являться и решением неравенства A ( x ) B ( x ) . Мы приняли, что q — решение неравенства A ( x ) + c B ( x ) + c , тогда A ( q ) + c B ( q ) + c , из обеих частей вычтем число c , получим A ( q ) B ( q ) , где q – решение неравенства A ( x ) B ( x ) .

Таким образом, неравенства A ( x ) B ( x ) и A ( x ) + c B ( x ) + c являются равносильными. Для наглядности укажем пример: x > 2 и x − 5 > 2 − 5 – равносильные неравенства, а, учитывая рассматриваемое выше утверждение, равносильным им является и неравенство x − 5 > − 3 .

1. Свойство, которое мы доказали выше, возможно расширить: прибавив к левой и правой частям неравенства одно и то же выражение с учетом соблюдения ОДЗ данного неравенства, получим равносильное неравенство.

Пример 3

Исходному неравенству x 7 будет равносильно неравенство x + ( 12 · x − 1 ) 7 + ( 12 · x − 1 ) .

1. Указанные выше равносильные преобразования дают как следствие еще одно действие, пожалуй, основное в процессе преобразования неравенств: перенос любого слагаемого из одной части неравенства в другую с противоположным знаком служит равносильным преобразованием.

Пример 4

Исходному неравенству 3 · x − 5 · y > 12 равносильно неравенство 3 · x > 12 + 5 · y .

1. Равносильным преобразованием также является умножение или деление обеих частей неравенства на одно и то же положительное число. И, умножив (или разделив) обе части неравенства на одно и то же отрицательное число, поменяв при этом знак неравенства на противоположный ( на > , > на , ≤ на ≥ , а ≥ на ≤ ), получим равносильное неравенство.

Доказательство 3

Докажем сначала первую часть утверждения. Допустим, задано неравенство A ( x ) B ( x ) и c – некое положительное число. Приведем доказательство, что A ( x ) B ( x ) и A ( x ) · c B ( x ) · c — равносильные неравенства. Примем q как решение заданного неравенства, в таком случае верным будет числовое неравенство A ( q ) B ( q ) . Опираясь на свойства числовых неравенств, можем утверждать, что, умножив обе части верного числового неравенства на положительное число, получим верное числовое неравенство. Производим умножение на заданное число c , что дает нам A ( q ) · c B ( q ) · c . Это значит, что q — решение неравенства A ( x ) · c B ( x ) · c .

Теперь в обратную сторону: примем q как решение неравенства A ( x ) · c B ( x ) · c , в таком случае: A ( q ) · c B ( q ) · c . Разделим обе части этого числового неравенства на положительное число c (опираясь на свойства числовых неравенств), что даст нам верное числовое неравенство A ( q ) B ( q ) . Отсюда можно сделать вывод, что q — решение неравенства A ( x ) B ( x ) . Так, мы доказали, что при положительном числе c неравенства A ( x ) B ( x ) и A ( x ) · c B ( x ) · c являются равносильными.

Таким же образом приводится доказательство второй части утверждения. Здесь можно опереться на свойство умножения и деления числовых неравенств на отрицательное число при смене знака неравенства на противоположный.

Задано неравенство 2 · x ≤ 5 . Умножим его левую и правую части на положительное число 3 , что даст нам равносильное неравенство 6 · x ≤ 15 .

Задано неравенство — 2 3 · z 1 . Разделим левую и правую его части на отрицательное число — 2 3 , сменив знак неравенства. Получим z > — 1 1 2 — неравенство, равносильное заданному.

Расширим и это свойство неравенств:

• умножив обе части заданного неравенства на одно и то же выражение, положительное при любых значениях переменных из ОДЗ заданного неравенства, не изменяющее ОДЗ, получим равносильное неравенство;
• умножив обе части неравенства на одно и то же выражение, отрицательное при любых значениях переменных из ОДЗ заданного неравенства и не изменяющее ОДЗ, а также изменив знак равенства на противоположный, получим равносильное неравенство.

Пример 7

Задано неравенство x > 1 . Умножим его правую и левую части на выражение x 2 + 1 , положительное на всей ОДЗ, и получим равносильное неравенство x · ( x 2 + 1 ) > 1 · ( x 2 + 1 ) .

В целом, есть и другие равносильные преобразования, однако, они не так распространены и скорее имеют отношение к конкретному виду неравенств, например, к логарифмическим неравенствам. Познакомиться с ними можно подробнее в соответствующей теме.

Результат неравносильных преобразований неравенств

Сколь уж существуют равносильные преобразования, имеют место и неравносильные. Такие действия приводят к искажению заданного неравенства и дают в итоге решение, не являющееся истинным для исходного неравенства. Случается, что и при неравносильных преобразованиях получается верный ответ, но это не более чем случайность.

Собственно, вывод очевиден: решая неравенства, производить только равносильные преобразования.

Разберем примеры для лучшего понимания теории.

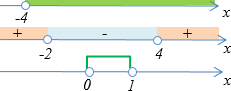
Пусть заданы неравенства x > − 2 и 1 x — 1 x + x > — 2 . Решением первого будет числовой промежуток ( − 2 , + ∞ ) , а второго – множество — 2 , 0 ∪ 0 , + ∞ .

Пусть необходимо решить второе неравенство.

Конечно, сазу приходит мысль об упрощении левой части приведением слагаемых, произведя замену просто на х, что даст переход к простому неравенству x > − 2 . Однако мы намеренно не учтем, что переход надо осуществить на ОДЗ переменной х ( х ≠ 0 ) , тогда предложенное выше преобразование даст нам неравносильное неравенство x > − 2 , а следовательно – неверный ответ ( − 2 , + ∞ ) взамен нужного — 2 , 0 ∪ 0 , + ∞ .

Посмотрим с другой стороны:

Мы решим неравенство x > − 2 . При этом нам захотелось заменить его якобы равносильным неравенством 1 x — 1 x + x > — 2 . Однако оно не является таковым: нуль не служит его решением, однако служит решением исходного неравенства. Суть в том, что выражение в его левой части тождественно равно не на всей области допустимых значений исходного неравенства: когда х = 0 , неравенство не равно x (при х = 0 оно не определено). Совершенные действия приведут нас к неверному ответу — 2 , 0 ∪ 0 , + ∞ взамен правильного ( − 2 , + ∞ ) .

Признак вероятного неравносильного преобразования – сужение области допустимых значений. Вновь обратимся к примеру выше: когда мы производили переход от неравенства x > − 2 к неравенству 1 x — 1 x + x > — 2 , произошло сужение ОДЗ со всего множества действительных чисел до множества без нуля. Такое положение вещей точно указывает на то, что полученное в итоге неравенство никак не будет равносильным исходному, т.е. такой переход не приведет к необходимому верному результату.

Неравносильные преобразования чаще всего происходят при невнимательном использовании свойств корней, логарифмов и модуля. Эти моменты будут детально рассмотрены в темах о решении неравенств соответствующих видов.

40. Алгебра Читать 0 мин.

40.710. Равносильные системы

Два неравенства являются равносильными, если множества их решений совпадают. При решении неравенств иногда приходится переходить от одного неравенства к другому, более простому. Рассмотрим несколько равносильных переходов: для решения иррациональных, показательных, логарифмических неравенств, неравенств с модулем, дробно-рациональных неравенств.

1. Равносильные переходы для решения иррациональных неравенств

Для избавления от радикалов в иррациональных неравенствах требуется умение возводить обе части неравенства в соответствующую степень. Однако нужно быть осторожными при возведении в четную степень, если хотя бы одна из частей неравенства отрицательная. Неосторожное возведение в квадрат неравенства может повлечь за собой приобретение или потерю решений.

Корни четной степени извлекаются только из неотрицательных чисел, это непосредственно относится к возведению корня четной степени $ \sqrt[2n] $ в соответствующую четную степень, после чего $f(x)$ стоит уже не под корнем, а значит, лишено неявного ограничения $f(x)\geq 0$. Следовательно, это неявное ограничение мы должны учесть, однако, учитываем мы его для меньшего подкоренного выражения (т.к. для большего это ограничение выполнится автоматически).

$\sqrt[2n]\geq \sqrt[2n]\leftrightarrow \left\< \begin f(x)\geq g(x) \\ g(x)\geq 0. \end \right. $

Пример. Решите неравенство

Решение. Применим равносильный переход:

$\left\< \begin x^<2>-5x+6\geq 0 \\ (x-3)(x-1)\geq 0 \end \right. \leftrightarrow \left\< \begin (x-2)(x-3)\geq 0 \\ (x-3)(x-1)\geq 0 \end \right. $

Видим, что решением системы является промежуток $x\in (-\infty ;1]\cup \lbrack 3;\infty )$

Ответ: $x\in (-\infty ;1]\cup \lbrack 3;\infty )$

Встречаются такие неравенства, в которых корень сравнивают с выражением. Тогда тоже пользуемся возведением в квадрат для избавления от иррациональности, однако, накладываем дополнительное ограничение – неотрицательность выражения, поскольку значение корня четной степени – число неотрицательное.

$\sqrt[2n] &lt g(x) \leftrightarrow \left\ < \begin f(x)&lt g^<2n>(x), \\ f(x)\geq 0, \\ g(x)>0. \end \right. $

$\sqrt[2n]\leq g(x)\leftrightarrow \left\< \begin f(x)\leq g^<2n>(x), \\ f(x)\geq 0, \\ g(x)\geq 0. \end \right. $

Пример. Решите неравенство

$\sqrt 0 \end \right. \leftrightarrow \left\< \begin x+5 -7 \end \right. \leftrightarrow \left\< \begin x^<2>-15x+44>0 \\ x\geq -5 \\ x 0 \\ x\geq -5 \\ x g(x)\leftrightarrow \left[ \begin \left\< \begin f(x)>g^<2n>(x) \\ g(x)\geq 0, \end \right. \\ \left\< \begin f(x)\geq 0, \\ g(x) 7-x$

Воспользуемся равносильным переходом.

Пример. Решите неравенство $\sqrt[3]>\sqrt[3]<2x+1>$

Решение. Воспользуемся равносильным переходом:

$x 1$, тогда неравенство $a^\vee a^$ равносильно неравенству $f\vee g$.

В этом правиле последнее неравенство имеет тот же знак, что и первое, т.к. показательная функция с основанием $a>1$ возрастает.

Пример. Решите неравенство: $0,1^+4x> 0;$

Ответ $x\in (-\infty ;-2)\cup (-2;+\infty )$.

Ответ: $x\in (-\infty ;-2)\cup (-2;+\infty )$

Если неизвестная входит как в основание, так и в показатель степени, то заранее неизвестно, будет ли основание степени больше или меньше единицы, поэтому при решении неравенства нужно учитывать оба этих случая. Если неравенство строгое, то получаем следующий равносильный переход:

$(\phi (x))^ &gt (\phi (x))^\Leftrightarrow \left[ \begin \left\< \begin f(x)>g(x) \\ \phi (x) &gt 1 \end \right. \\ \left\< \begin f(x) &lt g(x) \\ 0 &lt \phi (x) (x+5)^<4>$

Используем следующий равносильный переход:

Если неравенство нестрогое, то нужно дополнительно рассмотреть случай – основание равно единице, т.к. тогда получается, что единица в любой степени равна единице, неравенство выполнится. Т.е. получаем следующий равносильный переход:

$(\phi (x))^\geq (\phi (x))^\Leftrightarrow \left[ \begin \left\< \begin f(x)>g(x) \\ \phi (x)>1 \end\right. \\ \left\< \begin f(x) &lt g(x) \\ 0 0 \end \right. \leftrightarrow \left\< \begin x\neq 0 \\ x>0 \end \right. $

Используем следующий равносильный переход:

$\left[ \begin \left\< \begin x^<2>\geq -(x^<2>-4) \\ \frac<4><9>x>1 \end \right. \\ \left\< \begin x^<2>\leq -(x^<2>-4) \\ 0 &lt \frac<4><9>x &lt 1 \end \right. \\ \frac<4><9>x=1 \end \right. \leftrightarrow \left[ \begin \left\< \begin x^<2>+x^<2>-4\geq 0 \\ x>\frac<9> <4>\end \right. \\ \left\< \begin x^<2>+x^<2>-4\leq 0 \\ 0 &lt \frac<<>><9>x &lt \frac<9> <4>\end \right. \\ x=\frac<9> <4>\end \right. \leftrightarrow \left[ \begin \left\< \begin 2x^<2>+4\geq 0 \\ x>\frac<9> <4>\end \right. \\ \left\< \begin 2x^<2>+4\leq 0 \\ 0 &lt x &lt \frac<9> <4>\end \right. \\ x=\frac<9> <4>\end \right. \leftrightarrow \left[ \begin \left\< \begin 2(x^<2>+2)\geq 0 \\ x>\frac<9> <4>\end \right. \\ \left\< \begin 2(x^<2>+2)\leq 0 \\ 0 &lt x &lt \frac<9> <4>\end \right. \\ x=\frac<9> <4>\end \right. \leftrightarrow $

Таким образом, решение неравенства: $x\in \lbrack \frac<9><4>;\infty )$

Ответ $x\in \lbrack 2,25;\infty )$

3. Равносильные переходы для решения логарифмических неравенств

Метод решений простейших логарифмических неравенств опирается на монотонность логарифмической функции, т.е. на правило отбрасывания логарифмов. Однако есть отличие от аналогичного правила отбрасывания оснований, которое объясняется тем, что при отбрасывании логарифмов расширяется ОДЗ неравенства. Значит, выражения, стоящие под логарифмами после отбрасывания последних могут стать отрицательными или равными нулю, следовательно, мы должны дополнительно учесть, что подлогарифмическое выражение положительно.

Если неизвестная входит как в основание, так и под знак логарифма, то заранее неизвестно, будет ли основание больше или меньше единицы, поэтому при решении неравенства нужно учитывать оба этих случая.

Воспользуемся равносильным переходом:

$\left[ \begin \left\< \begin 2-x>1+x \\ 2-x>0 \\ 1+x>0 \\ 1+x>1 \end \right. \\ \left\< \begin 2-x &lt 1+x \\ 2-x>0 \\ 1+x>0 \\ 0 &lt 1+x &lt 1 \end \right. \end \right. \leftrightarrow \left[ \begin \left\< \begin -x-x>1-2 \\ -x>-2 \\ x>-1 \\ x>0 \end \right. \\ \left\< \begin -x-x &lt 1-2 \\ <-x>-2> \\ -1> \\ -1 &lt x &lt 0 \end \right. \end \right. \leftrightarrow \left[ \begin \left\< \begin -2x>-1 \\ x &lt 2 \\ x>-1 \\ x>0 \end \right. \\ \left\< \begin -2x &lt -1 \\ x &lt 2 \\ x>-1 \\ <-1 &lt x &lt 0>\end \right. \end \right. \leftrightarrow \left[ \begin \left\< \begin x &lt 0,5 \\ x &lt 2 \\ x>-1 \\ x>0 \end \right. \\ \left\< \begin x>0,5 \\ x &lt 2 \\ x>-1 \\ <-1 &lt x &lt 0>\end \right. \end \right. $

Решением первой системы является интервал (0;0,5)

При решении неравенств второй системы видим, что пересечений решений нет.

Таким образом, решением совокупности является интервал (0;0,5)

Пример. Решите неравенство

Воспользуемся равносильным переходом:

$\left[ \begin \left\< \begin x^<2>-2x-8\geq x^ <2>\\ x^<2>-2x-8>0 \\ x^<2>>0 \\ x>1 \end \right. \\ \left\< \begin x^<2>-2x-8\leq x^ <2>\\ x^<2>-2x-8>0 \\ x^<2>>0 \\ 0 &lt x &lt 1 \end \right. \end \right. \leftrightarrow \left[ \begin \left\< \begin x^<2>-2x-8-x^<2>\geq 0 \\ (x-4)(x+2)>0 \\ x\neq 0 \\ x>1 \end\right. \\ \left\< \begin x^<2>-2x-8-x^<2>\leq 0 \\ (x-4)(x+2)>0 \\ x\neq 0 \\ 0 &lt x &lt 1 \end \right. \end \right. \leftrightarrow \left[ \begin \left\< \begin -2x-8\geq 0 \\ (x-4)(x+2)>0 \\ x\neq 0 \\ x>1 \end \right. \\ \left\< \begin -2x-8\leq 0 \\ (x-4)(x+2)>0 \\ x\neq 0 \\ 0 &lt x &lt 1 \end \right. \end \right. $

$\left[ \begin \left\< \begin -2(x+4)\geq 0 \\ (x-4)(x+2)>0 \\ x\neq 0 \\ x>1 \end \right. \\ \left\< \begin -2(x+4)\leq 0 \\ (x-4)(x+2)>0 \\ x\neq 0 \\ 0 &lt x &lt 1 \end \right. \end \right. \leftrightarrow \left[ \begin \left\< \begin x+4\leq 0 \\ (x-4)(x+2)>0 \\ x\neq 0 \\ x>1 \end \right. \\ \left\< \begin x+4\geq 0 \\ (x-4)(x+2)>0 \\ x\neq 0 \\ 0 &lt x &lt 1 \end \right. \end \right. $

$\left\< \begin x+4\leq 0 \\ (x-4)(x+2)>0 \\ x\neq 0 \\ x>1 \end \right. \leftrightarrow \left\< \begin x\leq -4 \\ (x-4)(x+2)>0 \\ x\neq 0 \\ x>1 \end \right. $

видим, что для указанной системы нет решений, т.к. и $x>1$

$\left\< \begin x+4\geq 0 \\ (x-4)(x+2)>0 \\ x\neq 0 \\ 0 &lt x &lt 1 \end \right. \leftrightarrow \left\< \begin x\geq -4 \\ (x-4)(x+2)>0 \\ x\neq 0 \\ 0 &lt x &lt 1 \end \right. $

$\left\< \begin x\geq -4 \\ (x-4)(x+2)>0 \\ x\neq 0 \\ 0 &lt x &lt 1 \end\right. $

При нанесении решений каждого неравенства системы на числовую прямую видим, что пересечений решений нет. Значит, неравенство не имеет решений.

Ответ: решений нет.

4. Равносильные переходы для решения неравенств, содержащих знак модуля

Если модуль меньше функции, то избавляемся от модуля, но взамен получаем систему из двух неравенств. Учитываем случаи: если число под модулем положительно и если число под модулем отрицательно:

$\left\vert f(x)\right\vert &ltg(x) \leftrightarrow \left\< \begin f(x) &lt g(x) \\ f(x)>-g(x), \end \right. $

$\left\vert f(x)\right\vert \leq g(x)\leftrightarrow \left\< \begin f(x)\leq g(x) \\ f(x)\geq -g(x), \end \right. $

Этот метод работает всегда, даже если выражение $g(x)$ отрицательно. Убедимся в этом на примерах.

Пример. Решите неравенство: -5, \end \right. \leftrightarrow \left\< \begin x &lt 8 \\ x>-2 \end \right. $

Пример. Решите неравенство: $\left\vert x-3\right\vert &lt -5$

Решение. Воспользуемся равносильным переходом:

$\left\< \begin x-3 &lt -5 \\ x-3>-5 \end \right. \leftrightarrow \left\< \begin x &lt -2 \\ x>8 \end\right. $

Ответ: решений нет

Рассмотренный пример наглядно демонстрирует, что метод работает всегда. Мы помним, что модуль числа по определению является величиной неотрицательной. В примере модуль меньше отрицательного числа, очевидно, что такое неравенство не имеет решений.

Пример. Решите неравенство

$\left\vert x+4\right\vert &lt 2x$

Воспользуемся равносильным переходом.

$\left\< \begin x+4 &lt 2x \\ x+4>-2x \end \right. \leftrightarrow \left\< \begin x+4-2x &lt 0 \\ x+4+2x>0 \end \right. \leftrightarrow \left\< \begin -x+4 &lt 0 \\ 3x+4>0 \end \right. \leftrightarrow \left\< \begin x>4 \\ x>-\frac<4> <3>\end \right. $

Решением системы является луч (4;∞).

Ответ: $x\in (4;\infty )$

Пример. Решите неравенство

$\left\vert x+2\right\vert \leq 5x$

Воспользуемся равносильным переходом.

$\left\< \begin x+2\leq 5x \\ x+2\geq -5x \end \right. \leftrightarrow \left\< \begin x+2-5x\leq 0 \\ x+2+5x\geq 0 \end \right. \leftrightarrow \left\< \begin -4x\leq -2 \\ 6x\geq -2 \end \right. \leftrightarrow \left\< \begin x\geq 0,5 \\ x\geq -\frac<1> <3>\end \right. $

Решением системы является луч (0,5;∞).

Ответ: $x\in (0,5;\infty )$

Если модуль больше выражения, то здесь иной равносильный переход.

$\left\vert f(x)\right\vert >g(x)\leftrightarrow \left\< \begin f(x)>g(x) \\ f(x) &lt -g(x) \end \right. $

$\left\vert f(x)\right\vert \geq g(x)\leftrightarrow \left\< \begin f(x)\geq g(x) \\ f(x)\leq -g(x) \end \right. $

Другими словами, мы рассматриваем два случая: 1) сначала просто игнорируем модуль — решаем обычное неравенство; 2) затем по сути раскрываем модуль со знаком «минус», а затем умножаем обе части неравенства на −1, меня при этом знак. При этом варианты объединены квадратной скобкой, т.е. перед нами совокупность двух требований.

Пример. Решите неравенство

$\left\vert x-7\right\vert >8x$

Воспользуемся равносильным переходом.

$\left[ \begin x-7>8x \\ x-7 &lt -8x \end \right. \leftrightarrow \left[ \begin x-7-8x>0 \\ x-7+8x &lt 0 \end \right. \leftrightarrow \left[ \begin -7x>7 \\ 9x &lt 7 \end\right. \leftrightarrow \left[ \begin x &lt 1 \\ x &lt \frac<7> <9>\end \right. $

Решением совокупности является луч (-∞;1).

Ответ: $x\in (-\infty ;1)$

Пример. Решите неравенство

$\left\vert 2x+8\right\vert \geq x-5$

Воспользуемся равносильным переходом.

$\left[ \begin 2x+8\geq x-5 \\ 2x+8\leq -(x-5) \end \right. \leftrightarrow \left[ \begin 2x-x\geq -5-8 \\ 2x+x\leq 5-8 \end \right. \leftrightarrow \left[ \begin 2x-x\geq -5-8 \\ 2x+x\leq 5-8 \end \right. \leftrightarrow \left[ \begin x\geq -13 \\ 3x\leq -3 \end \right. \leftrightarrow \left[ \begin x\geq -13 \\ x\leq -1 \end \right. $

Решением совокупности является луч все множество действительных значений

Ответ: $x\in (-\infty ;\infty )$

5. Метод расщепления неравенств

Ключевой момент в решении неравенства – преобразование его к виду, в котором левая часть представляет собой произведение каких-либо функций, а правая – равна нулю. Дробно-рациональные неравенства $\frac\vee 0$ можно привести к равносильной системе:

$\frac\geq 0\leftrightarrow \left[ \begin \left\< \begin f(x)\geq 0 \\ g(x)>0 \end \right. \\ \left\< \begin f(x)\leq 0 \\ g(x) &lt 0 \end \right. \end\right. $

$\frac\leq 0\leftrightarrow \left[ \begin \left\< \begin f(x)\leq 0 \\ g(x)>0 \end \right. \\ \left\< \begin f(x)\geq 0 \\ g(x) &lt 0 \end \right. \end \right. $

То есть иными словами, дробь положительна, когда числитель и знаменатель одного знака; дробь отрицательна, когда числитель и знаменатель разных знаков.

Произведение двух множителей равносильно совокупности систем:

$f(x)\cdot g(x)\geq 0\leftrightarrow \left[ \begin \left\< \begin f(x)\geq 0 \\ g(x)\geq 0 \end \right. \\ \left\< \begin f(x) \leq 0 \\ g(x)\leq 0\end \right. \end \right. $

$f(x)\cdot g(x)\leq 0\leftrightarrow \left[ \begin \left\< \begin f(x)\leq 0 \\ g(x)\geq 0 \end \right. \\ \left\< \begin f(x)\geq 0 \\ g(x)\leq 0 \end \right. \end \right. $

То есть иными словами, произведение двух множителей положительно, когда оба множителя одного знака; произведение отрицательно, когда оба множителя разных знаков.

Пример. Решите неравенство $\frac\geq 0$

Решение. Воспользуемся равносильным переходом.

$\left[ \begin \left\< \begin x-15\geq 0 \\ x-4>0 \end \right. \\ \left\< \begin x-15\leq 0 \\ x-4 &lt 0 \end \right. \end \right. \leftrightarrow \left[ \begin \left\< \begin x\geq 15 \\ x>4 \end \right. \\ \left\< \begin x\leq 15 \\ x &lt 4 \end \right. \end \right. $

Решение первой системы – луч [15;∞)

Решение второй системы – открытый луч (-∞;4).

Значит, решением совокупности является объединение полученных решений, т.е. $x\in (-\infty ;4)\cup \lbrack 15;\infty )$

Ответ: $x\in (-\infty ;4)\cup \lbrack 15;\infty )$

Пример. Решите неравенство $\frac<2x-3>\leq 0$

Решение. Воспользуемся равносильным переходом.

$\left[ \begin \left\< \begin 2x-3\leq 0 \\ x-1>0 \end \right. \\ \begin 2x-3\geq 0 \\ x-1 &lt 0 \end \end \right. \leftrightarrow \left[ \begin \left\< \begin 2x\leq 3 \\ x>1 \end \right. \\ \begin 2x\geq 3 \\ x &lt 1 \end \end \right. \leftrightarrow \left[ \begin \left\< \begin x\leq 1,5 \\ x>1 \end \right. \\ \begin x\geq 1,5 \\ x &lt 1 \end \end \right. $

Решение первой системы – полуинтервал (1;1,5]

Вторая система не имеет решений.

Значит, решением совокупности является $x\in (1;1,5]$

Использование равносильных переходов и нестандартных приемов при решении иррациональных и логарифмических уравнений

Разделы: Математика

Цели урока:

1. показать широкие возможности использования равносильных переходов при решении уравнений,
2. показать некоторые нестандартные приёмы при решении иррациональных уравнений.

Анализ решения уравнений при проведении ЕГЭ показывает, что с уравнениями обычно складывается странное положение. Эти задачи не считаются обычно трудными, и большинство решающих с ними, по их мнению, справляются. В то же время, многим не засчитываются эти решения из-за грубых ошибок.

Почему же так происходит?

Дело в том, что у многих, окончивших среднюю школу, имеется огромный разрыв между приобретёнными техническими, вычислительными навыками и сознательным пониманием тех теоретических и логических основ, без которых правильно решать уравнения невозможно.

Упростить уравнение с помощью безошибочно проведённых выкладок может большинство, но заметить, как и почему эти выкладки приводят к приобретению или потере решения может далеко не каждый, а очень многие об этом даже и не задумываются.

Или взять вопрос о проверке. Одни считают, что это прихоть учителей, которой нужно волей или неволей подчиняться. Другие проверяют всё подряд. Такие мнения основаны на непонимании того, что такое проверка и какое значение она должна занимать в решении.

Короче говоря, всякий должен владеть тем теоретическим минимумом, который необходим для решения уравнений.

Остановимся на этом минимуме! [1]

1. Прежде всего, что такое ОДЗ – область допустимых значений уравнения?

Областью допустимых значений (ОДЗ) уравнения называется множество значений неизвестного, при котором имеют смысл (определены) его левая и правая части.

Уравнение 1:

ОДЗ ,

ОДЗ .

При решении уравнения ОДЗ изменилась. Но это ли привело к появлению посторонних корней, мы узнаем позже.

Уравнение 2:

ОДЗ

ОДЗ

При решении уравнения ОДЗ изменилась. Но это ли привело к появлению посторонних корней, мы узнаем позже.

Прежде ответим на следующие вопросы.

2. Какое уравнение является следствием другого?.

Ответ: Если все корни первого уравнения, являются корнями второго уравнения, то второе уравнение называется следствием первого.

3. Какие уравнения являются равносильными?

Ответ: Уравнения, имеющие одно и то же множество корней, называются равносильными.

4. Какие преобразования приводят к нарушению равносильности?

Ответ: Посторонние корни могут получиться:

1. при умножении обеих частей уравнения на выражение, содержащее неизвестные,
2. при возведении в чётную степень,
3. использование различных логарифмических формул, в частности заменяя на , мы расширяем ОДЗ уравнения,
4. при взаимном уничтожении подобных членов, может произойти снятие ограничений, при которых уничтожаемые слагаемые должны иметь смысл, и тем самым может произойти расширение ОДЗ.

Все эти преобразования приводят к образованию новых корней, которые можно отбросить с помощью проверки или следить, чтобы равносильность не нарушалась.

Также равносильность может нарушиться в другую сторону, т.е. может произойти потеря корней, что потом восстановить будет невозможно. Это может быть в следующих случаях:

1. при делении обеих частей уравнения на выражение, содержащее неизвестное,
2. обратная замена логарифма произведения на сумму логарифмов приводит к сужению ОДЗ, и поэтому недопустимо, при переходе к новому основанию логарифма,
3. введение универсальной тригонометрической подстановки.
4. Какие преобразования приводят к уравнению следствию?

Ответ: Все преобразования, которые ведут к расширению области корней, или оставляют её неизменной, приводят к уравнению следствию.

6. Одинаков ли будет ответ на эти два вопроса (4 и 5)?

Ответ: как видим ответы разные.

Равносильны ли уравнения? Объясните, какое преобразование было выполнено при переходе от первого уравнения ко второму и может ли оно привести к нарушению равносильности?

1. и ; (Да)
2. и ; (Да)
3. и ; (Нет)
4. и ; (Да)
5. и . (Нет)

Значит при переходе ко второму уравнению в случаях а), б), г) нужна оговорка (они равносильны в своей ОДЗ), а в случаях в) и д) нужно наложить условие (в случае «в»: , в случае «д»: ).

При каком условии равносильны уравнения:

1. и Ответ: при .
2. и Ответ: при .

Вернёмся к уравнениям:

Уравнение 1:

(I)

(II)

— посторонний корень.

Ответ: .

Вопрос: За счёт чего появился посторонний корень?

Ответ: Т.к. уравнение является уравнением следствием не только для уравнения , но и для постороннего уравнения . Таким образом при возведении в квадрат корни не теряются, но посторонние корни появиться могут.

Уравнения (I) и (II) неравносильны, но они равносильны на области .

Заменим уравнение (I) на равносильную систему:

Рассмотрим Уравнение 2:

(III)

(IV)

— посторонний корень,

Ответ: .

Вопрос: За счёт чего появился посторонний корень?

Ответ: За счёт расширения ОДЗ.

Уравнения (III) и (IV) неравносильны, но они неравносильны в ОДЗ первого уравнения, то есть заменим (III) на равносильную систему:

Рассмотрим следующие уравнения:

Уравнение 3: [3]

Уравнение 4: [3]

Уравнение 5: [3]

Все эти уравнения имеют вид .

В ОДЗ обе части неотрицательны, и возведение в квадрат даёт равносильное уравнение . Поэтому

[2]

При таком способе решения достаточно проверить неотрицательность одной из функций – можно выбрать более простую.

Применяя данный способ, решим каждое из этих уравнений.

Уравнение 3:

Ответ:

Уравнение 4:

Ответ:

Уравнение 5:

.

Ответ: корней нет.

Перейдём к логарифмическим уравнениям:

В тетрадях своих учащихся, я встретилась со следующими решениями логарифмических уравнений. Ребята были уверены, что решили всё правильно. Получив тетрадь разочаровывались, увидев оценку ниже, чем рассчитывали. Вам предстоит найти эти ошибки:

Пример 1:

(I)

(II)

Ответ: .

Пример 2:

(I)

(II)

Т.к. , то корней нет

Ответ: корней нет.

Ошибки состоят в следующем: в процессе решения в обоих случаях уравнение (I) заменено на уравнение (II), не являющееся его следствием. В этом случае имеется корень уравнения (I), не являющийся корнем уравнения (II). Поэтому произошла потеря корня. В примере 1 , В примере 2 .

В примере 1 корень был потерян при переходе к другому основанию логарифма. Перейдя к основанию, тем самым было исключено из ОДЗ число , которое является корнем исходного уравнения.

В примере 2, убрав показатель 4, нужно было перейти к равносильному уравнению вида

.

Подведём итог:

Таким образом, в процессе решения, каждое уравнение заменяется на какое-то новое, а у нового уравнения естественно могут быть новые корни. Проследить за изменением корней, не допустить потери и отбросить лишние корни – это и есть задача правильного решения уравнений.

Нестандартные приёмы при решении уравнений.

Кроме того, хочется сказать, что не всегда уравнения решают по алгоритму. Хотя внешний вид уравнений стандартен, но требует нестандартного подхода.

Уравнение 1: .

Решение «в лоб» даёт уравнение четвёртой степени, которое решить практически невозможно. Используем для решения метод оценки:

, , поэтому сумма.

Делаем вывод: корней нет.

Уравнение 2:

Решение: Данное уравнение можно решить стандартным способом, что приводит к «большим» числам в квадратном уравнении.

Однако, его можно решить проще: один корень легко находится подбором, это . Левая часть уравнения — сумма возрастающих функций есть функция возрастающая, т.е. монотонная на своей области определения, каждое своё значение принимающая при одном значении аргумента. Т.е. и значение 5 она принимает один раз при .

Ответ: .

Уравнение 3:

Решение: заметим, что сумма коэффициентов в каждом подкоренном выражении равна 0. Значит корень уравнения .

Возможно предположить, что ОДЗ состоит только из этого числа. Найдя ОДЗ, убеждаемся, что так оно и есть. Значит корень уравнения один .

Ответ: .

Уравнение 4:

Решение: т.к. левая часть является суммой двух неотрицательных слагаемых, то от уравнения перейдём к равносильной системе:

Ответ: .

Уравнение 5: [1]

Это уравнение можно переписать в виде

.

Итак, степени равны, основания равны. Чтобы не потерять корней, посмотрим, может ли основание быть равным 0 или 1. Так как выражение не имеет смысла, то число 0 не входит в ОДЗ, а потому не является корнем уравнения. Напротив, , очевидно, является корнем. Будем теперь искать корни, отличные от 0 и 1. Тогда, применяя указанное правило, получим , откуда находим второй корень уравнения .

Ответ: , .

Конечно, невозможно указать все методы решения «нестандартных» задач. Здесь приходится применять и графики, и самые различные свойства функций, и неравенства, и – последнее по счету, но первое по важности – логику.

Вывод: Сегодня на уроке мы постарались охватить тот минимум теоретических знаний, который необходим для решения уравнений. Знание этого минимума позволяет нам решать уравнения не допуская ошибок.

Список литературы:

1. Г.В. Дорофеев, М.К. Потапов, Н.Х. Розов «Пособие по математике для поступающих в вузы». Издательство «Наука» 1970.
2. С.И. Колесникова «Математика. Решение сложных задач единого государственного экзамена». Издательство «Айрис-пресс» 2006.
3. Г.В. Дорофеев, Г.К. Муравин, Е.А. Седова «Сборник заданий для проведения письменного экзамена по математике (курс А) и алгебре и началам анализа (курс Б) за курс средней школы. 11 класс». Издательство «Дрофа» 2006.