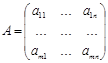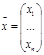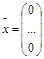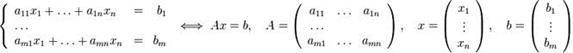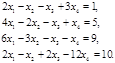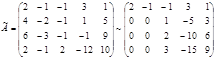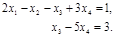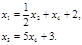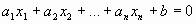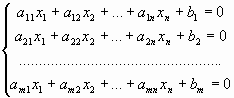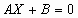Равносильные системы линейных уравнений матрицы

Равносильные системы уравнений, равносильные преобразования

В этой статье мы поговорим про равносильные системы уравнений. Здесь мы дадим соответствующее определение, а также разберем, какие существуют преобразования, позволяющие переходить от исходной системы уравнений к равносильной ей системе.

Навигация по странице.

Определение равносильных систем уравнений

В учебниках [1, с. 199; 2, с. 74] дается определение равносильных систем уравнений с двумя переменными:

Две системы уравнений с двумя переменными называются равносильными, если они имеют одни и те же решения или если обе системы не имеют решений.

В старших классах оно обобщается на системы с любым числом уравнений и переменных [3, с. 265] :

Две системы уравнений называются равносильными, если они имеют одни и те же решения или если обе системы не имеют решений.

Примеры равносильных и неравносильных систем приведем в следующем пункте.

Равносильны ли данные системы уравнений?

Чтобы сделать вывод о равносильности или неравносильности данных систем уравнений на основе определения, надо наперед знать решения этих систем. Приведем пример. Пусть нам известно, что системы уравнений и не имеют решений (это достаточно очевидно: первая содержит не имеющее решений уравнение 0·x=4 , а вторая – уравнение |x|=−1 ). А по определению системы уравнений, которые не имеют решений, равносильны.

Чтобы доказать неравносильность систем уравнений, достаточно привести одно частное решение, являющееся решением одной системы, но не являющееся решением другой. Например, легко обосновать, что системы уравнений и неравносильны. Действительно, пара (0, 0) является решением первой системы, при этих значениях переменных оба уравнения системы обращаются в верные числовые равенства 0=0 и 0=−0 , но не является решением второй, так как ее второе уравнение при подстановке этих значений дает неверное равенство 0−0=2 . А по определению решения равносильных систем должны быть одинаковыми.

А как доказать равносильность систем уравнений, если их решения неизвестны? Конечно, можно найти решения, после чего сделать вывод касательно равносильности на основе определения. Но иногда для этого решать системы необязательно, это касается тех случаев, когда видно, что одна система получена из другой при помощи некоторых так называемых равносильных преобразований. Их мы подробно изучим в следующем пункте, а пока приведем пример.

Рассмотрим две системы уравнений и . При внимательном взгляде на их записи можно заметить следующие вещи: уравнение второй системы есть результат почленного сложения соответствующих частей уравнений первой системы, а второе уравнение второй системы получено из второго уравнения первой системы посредством переноса слагаемого в другую часть. Описанные преобразования являются равносильными, и в результате их проведения получается система, равносильная исходной. Итак, указанные системы равносильны. А мы переходим к разбору основных равносильных преобразований.

Равносильные преобразования систем уравнений

Существует ряд преобразований, позволяющих преобразовать данную систему уравнений в равносильную ей систему. Они получили название равносильных преобразований, и нашли основное применение при решении систем уравнений. Эти преобразования можно считать свойствами систем уравнений. Рассмотрим и обоснуем основные из них.

Перестановка местами уравнений системы дает равносильную систему уравнений.

Доказательство этого утверждения очевидно. В силу определения решения системы уравнений любое отдельно взятое решение системы уравнений является решением каждого уравнения этой системы. Понятно, что оно является и решением каждого уравнения системы с этими же уравнениями, но переставленными местами, значит, является решением и системы с переставленными местами уравнениями.

К примеру, и — равносильные системы.

Если любое уравнение в системе заменить равносильным уравнением, то полученная система будет равносильна исходной.

Доказательство этого факта тоже лежит на поверхности. Любое решение системы уравнений является решением каждого уравнения системы. Мы также знаем, что равносильные уравнения имеют одинаковые решения. Поэтому, любое решение исходной системы уравнений будет решением всех уравнений системы, в которой какое-то уравнение заменено равносильным ему уравнением, а значит, и решением этой системы.

Важность доказанного свойства огромна: оно дает нам право на работу с отдельными уравнениями системы. С ними мы можем проводить всевозможные уже знакомые нам равносильные преобразования, например, перестановку местами слагаемых, перенос слагаемых из одной части в другую с противоположным знаком, умножение или деление обеих частей уравнения на отличное от нуля число и т.д.

Приведем пример. Пусть дана система . В ее первом уравнении можно выполнить умножение чисел, то есть, заменить его равносильным уравнением 12·x−y=1 . А во втором уравнении можно собрать все слагаемые в левой части, раскрыть скобки, после чего привести подобные слагаемые. В результате получится равносильная система более простого вида .

Если к левой и правой части одного из уравнений системы прибавить соответственно левую и правую часть другого уравнения системы, то полученная система будет равносильна исходной.

Для доказательства покажем, что любое решение изначальной системы уравнений является решением полученной, и обратно, что любое решение полученной системы является решением исходной. Это будет означать равносильность систем.

Любое решение начальной системы является решением каждого ее уравнения, оно обращает все уравнения в верные числовые равенства. Нам известно свойство числовых равенств, которое утверждает, что при почленном сложении верных числовых равенств получается верное равенство. Отсюда следует, что взятое нами решение начальной системы является решением уравнения, полученного в результате почленного прибавления к нему другого уравнения. Поэтому, это решение является решением и полученной системы уравнений, так как является решением каждого ее уравнения.

Теперь обратно. Возьмем любое решение полученной системы, оно является решением каждого ее уравнения, то есть, оно обращает их в верные числовые равенства. Существует свойство, позволяющее выполнять почленное вычитание верных числовых равенств. Вычтем из равенства, соответствующего уравнению, полученному в результате почленного сложения, равенство, соотетствующее прибавленному ранее уравнению. Это даст верное числовое равенство, отвечающее начальному уравнению системы до прибавления к нему другого уравнения. Отсюда следует, что взятое решение будет решением каждого уравнения исходной системы, а значит, и ее решением.

Приведем пример выполнения этого равносильного преобразования. Возьмем систему двух уравнений с двумя переменными . Прибавив к левой и правой части первого уравнения соответственно левую и правую часть второго, получим уравнение с одной переменной 3·y=3 , а система примет вид . Полученная система уравнений имеет более простой вид, но при этом равносильна исходной.

Понятно, что если система содержит три или большее число уравнений, то можно не ограничиваться почленным прибавлением к левой и правой части выбранного уравнения левой и правой части одного уравнения, а прибавлять левые и правые части двух, трех, да хоть всех остальных уравнений системы. В результате этих действий все равно получится равносильная система уравнений.

На доказанном равносильном преобразовании базируется один из методов решения систем уравнений – метод алгебраического сложения.

Если одно из уравнений системы представляет собой переменную, выраженную через другие переменные, то в любое другое уравнение системы можно подставить вместо этой переменной ее выражение, система, полученная в результате такого преобразования, равносильна исходной.

Приведем пример для пояснения. Возьмем систему . В ее первом уравнении переменная x выражена через y . Оставим первое уравнение системы без изменений, а во второе подставим вместо x ее выражение через y , то есть, 2·y−1 . В результате приходим к системе , которая равносильна исходной. Обоснуем это.

Пусть пара (x₀, y₀) – решение исходной системы, тогда x₀=2·y₀−1 и x₀+3·y₀−1=0 – верные числовые равенства. Докажем, что при этом равенство (2·y₀−1)+3·y₀−1=0 тоже верное, что будет доказывать, что (x₀, y₀) является решением системы, полученной после преобразования, а это будет означать, что полученная система имеет те же решения, что и исходная.

Легко показать, что при условии x₀=2·y₀−1 значения выражений x₀+3·y₀−1 и (2·y₀−1)+3·y₀−1 равны. Для этого составим их разность и покажем, что она равна нулю: x₀+3·y₀−1−((2·y₀−1)+3·y₀−1)= (x₀−(2·y₀−1))+(3·y₀−1−(3·y₀−1))= x₀−(2·y₀−1) , а полученное выражение равно нулю в силу равенства x₀=2·y₀−1 . Итак, справедливо равенство x₀+3·y₀−1=(2·y₀−1)+3·y₀−1 , но справедливо и равенство x₀+3·y₀−1=0 , а из них по свойству транзитивности вытекает справедливость равенства (2·y₀−1)+3·y₀−1=0 .

Аналогично доказывается, что любое решение системы уравнений является решением исходной системы. В итоге можно сделать вывод, что системы равносильны.

Суть доказательства рассматриваемого утверждения в общем виде та же. То есть, показывается, что любое решение исходной системы является решением системы, полученной после преобразования, и обратно.

Это равносильное преобразование дает разрешение на решение систем уравнений методом подстановки.

В заключение скажем, что обычно при решении систем уравнений разобранные равносильные преобразования используются сообща и иногда по нескольку раз. Дальше на практике Вы увидите это.

Системы линейных уравнений. Равносильные системы линейных уравнений. Решение системы линейных уравнений методом последовательного исключения переменных

(1)

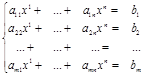
Составим матрицу при n-неизвестных.

Эту матрицу называют матрицей системы(1)илиосновной матрицей. Если к ней добавить столбец, то вновь полученную матрицу называют расширенной.

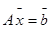
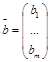
Систему (1) удобно переписать в виде , где А-матрица столбца неизвестных

— столбец свободных членов

Система (1) называется однородной, если вектор b-нулевой, в противном случае — неоднородной.

Система (1) называется совместной, если она имеет хотя бы одно решение, т.е. переменным ( 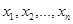) можно придать такие значения, которые будучи подставленными в (1) превращает уравнение в верное числовое равенство. Если система (1) решений не имеет, то ее называют несовместной.

Очевидно, что однородная система всегда совместна.

Однородная система линейных уравнений.Очевидно, что если какое-либо уравнение системы заменить суммой этого уравнения и любого другого уравнения, умноженного на некоторое число, то вновь полученная система будет => первоначальной. Множество решений таких систем совпадает. Так же очевидно, что если два уравнения системы переставить местами, так же получим эквивалентную систему. Это значит, что с матрицей системы можно производить элементарные преобразования 1 и 2 видов.

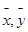
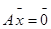
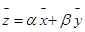
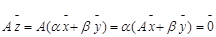
Пусть — решение однородной системы (2), покажем, что их линейная комбинация также будет решением этой системы ; .

Это означает, что множество всех решений однородной системы V является подпространством пространства | 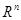. Размерность этого подпространства = n-r, где r – ранг матрицы А.

Пусть .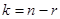

Базис линейного пространства V 1, f₂,…f_k>называется фундаментальной системой решения (ФСР) системы (2). Зная ФСР можно записать любое решение однородной системы (2).

Алгоритм решения однородной системы:

1.Выписываем матрицу системы.

2.Приводим матрицу к ступенчатому виду.

3.Переменные, соответствующие угловым коэффициентам в ступенчатой матрице, назовем зависимыми, а оставшиеся – независимыми. Затем выразим зависимые переменные через независимые. Кол-во зависимых = r(рангу матрицы), количество независимых (свободных) = k.

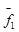
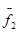
4.Векторы ФСР можно получить так: одной из свободных переменных придаем 1, а остальным – 0, и вычисляем значение зависимых переменных. Получаем , придавая значение 1 другой переменной, получим другой вектор и т.д., пока не получим ФСР.

5.Общее решение системы f будет иметь вид 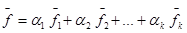, где α₁,α₂,…α_k — произвольные числа.

Неоднородные системы линейных ур-й. Метод Гаусса.

(1)

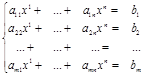
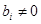
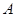
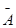
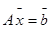
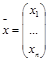
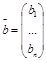
В системе (1) хотя бы одно из чисел . Обозначим — матрицу этой системы, — матрицу расширенную. Систему (1) можно переписать в векторном виде

(1), где , .

Наряду с системой (1) будем рассматривать однородную систему (2), которую назовем соответствующей системе (1).

(2)

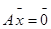
Неоднородная система может быть несовместной, т.е. не иметь решений.

Неоднородная система (1) совместна тогда и только тогда, когда ранг ее основной матрицы=рангу расширенной ( ).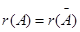

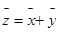
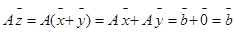
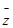
Пусть х – решение системы (1), а у – решение системы (2). Тогда -решение систем , т.о. — является решением системы (1)

Т.о. если к частному решению системы (1) прибавить какое-нибудь решение, соответствующей однородной системы (2), то снова получим решение системы (1).

Т.о. можно получить любое решение системы (1).

(3), где — общая неоднородная система; — общая однородная; — частная неоднородная

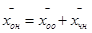
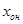
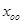
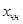
Поэтому для отыскания решения системы (1) необходимо найти какое-нибудь частное решение системы (1), найти все решения соответствующее неоднородной системы и воспользоваться формулой (3).

Метод Гаусса— классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Матрица A наз. основнойматрицей системы, b — столбцом свободных членов.

Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа:

На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.

На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из кот. выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.

Пример: Решить систему уравнений

Решение. Будем решать методом Гаусса. Выпишем расширенную матрицу системы и преобразуем её, вычитая первую строку, умноженную на 2, 3 и 1 соответственно из 2-ой, 3-ей и 4-ой строк:

Далее вторую строку, умноженную на 2 и 3, вычтем соответственно из третей и четвёртой строк:

Последняя матрица эквивалентна следующей ступенчатой системе:

Полученная упрощённая система представляет собой систему из двух уравнений для четырёх неизвестных. Следовательно, два из неизвестных можно выбрать за главные, а два — за свободные, через кот. будут выражены главные. В качестве главных неизвестных можно выбрать любую пару, если определитель, составленный из коэффициентов, стоящих перед ними, отличен от нуля (базисный

минор). В данной задаче в качестве главных неизвестных можно выбрать .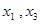

Действительно, определитель, составленный из их коэффициентов, отличен от нуля: .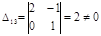

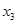
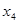
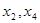
Теперь из второго уравнения выразим через . Затем подставим его в первое уравнение и найдём через . В итоге получим:

Переменные 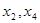принимают произвольные значения. Положив , общее решение системы можно записать в виде:

Равносильные системы линейных уравнений матрицы

Системы линейных уравнений

Линейное уравнение (л.у.) – уравнение вида

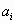
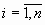
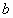
где – числа, называемые коэффициентами л.у., ,

– число, называемое свободным членом л.у.

Система линейных уравнений (СЛУ) – система вида

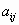
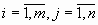
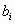
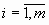
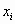
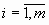
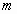
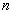
где – числа, называемые коэффициентами СЛУ, ,

– числа, называемые свободными членами СЛУ, ,

– переменные СЛУ, ,

– количество уравнений СЛУ,

– количество переменных СЛУ.

Сокращенная форма записи СЛУ (2)

, .

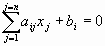
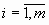
Матричная форма записи СЛУ (2)

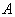
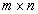
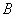
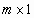
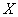
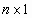
где – матрица коэффициентов СЛУ размерности ,

– вектор свободных членов СЛУ размерности ,

– вектор переменных СЛУ размерности ,

0 – нуль-вектор размерности .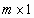

Квадратная СЛУ – СЛУ, состоящая из n уравнений с n переменными.

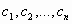
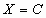
Решение СЛУ с n переменными – упорядоченная совокупность чисел ( для(4)), являющихся решением каждого из уравнений, входящих в систему.

1. Точные методы решения – методы решения, дающие точное решение задачи за конечное число арифметических и логических операций в предположении отсутствия округлений. Применяются для решения задач с малым числом переменных – не более 10 3 .

2. Итеративные методы решения – методы решения, дающие возможность получить решение с заданной точностью или точное решение. Применяются для решения задач со средним числом переменных – не более 10 6 . Требуют меньше вычислений, чем точные методы решения.

3. Вероятностные методы решения. Применяются для решения задач с большим числом переменных – более 10 6 .

Совместная СЛУ – СЛУ, имеющая одно или несколько решений.

Определенная СЛУ – совместная СЛУ, имеющая единственное решение.

Неопределенная СЛУ – совместная СЛУ, имеющая более одного решения.

Несовместная СЛУ – СЛУ, не имеющая ни одного решения.

Однородная СЛУ (ОСЛУ) – СЛУ, все свободные члены которой равны нулю

,

, ,

.

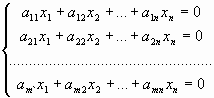
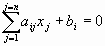
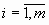
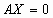
1. Любая ОСЛУ имеет хотя бы одно решение – тривиальное решение, т.е. .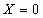

2. Для того чтобы ОСЛУ имела нетривиальные решения, необходимо и достаточно, чтобы ранг матрицы коэффициентов системы был меньше количества переменных системы.

Неоднородная СЛУ (НСЛУ) – СЛУ, у которой хотя бы один свободный член отличен от нуля

.

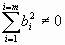
1. Для того чтобы НСЛУ была совместной СЛУ, необходимо и достаточно, чтобы ранг матрицы коэффициентов равен рангу расширенной матрицы (7).

2. Квадратная НСЛУ с вырожденной матрицей коэффициентов может быть совместной неопределенной системой или несовместной системой.

,

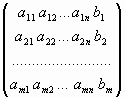
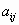
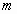
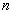
где – коэффициенты СЛУ, ,

– свободные члены СЛУ, ,

– количество уравнений СЛУ,

– количество переменных СЛУ.

Равносильные СЛУ – две СЛУ, множества решений которых совпадают.

1. Всякие две несовместные системы считаются равносильными.

Элементарные преобразования СЛУ :

— умножение некоторого уравнения системы на отличное от нуля число;

— прибавление к одному уравнению системы другого ее уравнения, умноженного на произвольное число;

— перестановка местами двух уравнений системы;

— перестановка местами двух неизвестных вместе с коэффициентами у всех уравнений.

Эквивалентные СЛУ – две СЛУ, полученные одна из другой с помощью элементарных преобразований.

1. Любые две эквивалентные СЛУ – равносильные.

2. Любая СЛУ приводится посредством элементарных преобразований к системе с трапециевидной матрицей.

3. Любая квадратная СЛУ с невырожденной матрицей коэффициентов A приводится посредством элементарных преобразований к системе с треугольной матрицей.