Равноускоренное прямолинейное движение его характеристики уравнения графики

Скорость. Ускорение. Равноускоренное прямолинейное движение

1. Реальное механическое движение — это движение с изменяющейся скоростью. Движение, скорость которого стечением времени изменяется, называют неравномерным движением.

При неравномерном движении координату тола уже нельзя определить но формуле ​ \( x=x_0+v_xt \) ​, так как значение скорости движения не является постоянным. Поэтому для характеристики быстроты изменения положения тела с течением времени при неравномерном движении вводят величину, называемую средней скоростью.

Средней скоростью ​ \( \vec_ <ср>\) ​ неравномерного движения называют физическую величину, равную отношению перемещении \( \vec \) тела ко времени ​ \( t \) ​, за которое оно произошло: ​ \( \vec_<ср>=\frac\) ​.

Записанная формула определяет среднюю скорость как векторную величину. В практических целях этой формулой можно воспользоваться для определения модуля средней скорости лишь в том случае, когда тело движется вдоль прямой в одну сторону. Если же нужно определить среднюю скорость движения автомобиля от Москвы до Санкт-Петербурга и обратно, чтобы рассчитать расход бензина, то эту формулу применить нельзя, поскольку перемещение в этом случае равно нулю и средняя скорость тоже равна нулю. Поэтому на практике при определении средней скорости пользуются величиной, равной отношению пути ​ \( l \) ​ ко времени ​ \( t \) ​, за которое этот путь пройден: \( v_<ср>=\frac\) . Эта скорость обычно называется средней путевой скоростью.

2. Важно, что, зная среднюю скорость неравномерного движения на каком-либо участке траектории, нельзя определить положение тела на этой траектории в любой момент времени. Например, если средняя скорость движения автомобиля за 2 часа 50 км/ч, то мы не можем сказать, где он находился через 0,5 часа от начала движения, через 1 час, 1,5 часа и т.п., поскольку он мог первые полчаса двигаться со скоростью 80 км/ч, затем какое-то время стоять, а какое-то время ехать в пробке со скоростью 20 км/ч.

3. Двигаясь по траектории, тело проходит последовательно все её точки. В каждой точке траектории оно находится в определённые моменты времени и имеет какую-то скорость.

Мгновенной скоростью называют скорость тела в данный момент времени в данной точке траектории.

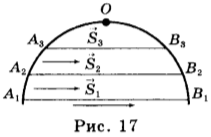
Предположим, некоторое тело совершает неравномерное прямолинейное движение (рис. 17), его скорость в точке О можно определить следующим образом: выделим на траектории участок AB, внутри которого находится точка О. Перемещение тела на этом участке — \( \vec_1 \) совершено за время \( t_1 \) . Средняя скорость движения на этом участке – \( \vec_<ср.1>=\frac \) . Уменьшим перемещение тела. Пусть оно равно \( \vec_2 \) , а время движения — ​ \( t_2 \) ​. Тогда средняя скорость за это время: \( \vec_<ср.2>=\frac \) . Еще уменьшим перемещение, средняя скорость на этом участке: \( \vec_<ср.3>=\frac \) .

При дальнейшем уменьшении перемещения и соответственно времени движения тела они станут такими маленькими, что прибор, например спидометр, перестанет фиксировать изменение скорости, и движение за этот малый промежуток времени можно считать равномерным. Средняя скорость на этом участке и есть мгновенная скорость тела в т.О.

Таким образом, мгновенной скоростью называют векторную физическую величину, равную отношению малого перемещения (​ \( \Delta<\vec> \) ​) к малому промежутку времени \( \Delta\) , за которое это перемещение произошло: ​ \( \vec=\frac<\Delta><\Delta> \) ​.

4. Одним из видов неравномерного движения является равноускоренное движение. Равноускоренным движением называют движение, при котором скорость тела за любые равные промежутки времени изменяется на одно и то же значение.

Слова «любые равные промежутки времени» означают, что какие бы равные промежутки времени (2 с, 1 с, доли секунды и т.п.) мы ни взяли, скорость всегда будет изменяться одинаково. При этом её модуль может как увеличиваться, так и уменьшаться.

5. Характеристикой равноускоренного движения, помимо скорости и перемещения, является ускорение.

Пусть в начальный момент времени ​ \( t_0=0 \) ​скорость тела равна ​ \( \vec_0 \) ​. В некоторый момент времени ​ \( t \) ​ она стала равной \( \vec \) . Изменение скорости за промежуток времени ​ \( t-t_0=t \) ​ равно ​ \( \vec-\vec_0 \) ​ (рис.18). Изменение скорости за единицу времени равно: \( \frac<\vec-\vec_0>\) . Эта величина и есть ускорение тела, она характеризует быстроту изменения скорости \( \vec=\frac<\vec-\vec_0>\) .

Ускорение тела при равноускоренном движении — векторная физическая величина, равная отношению изменения скорости тела к промежутку времени, за который это изменение произошло.

Единица ускорения ​ \( [a]=[v]/[t] \) ; ​ \( [a] \) ​​ = 1 м/с/1 с = 1 м/с 2 . 1 м/с 2 — это такое ускорение, при котором скорость тела изменяется за 1 с на 1 м/с.

Направление ускорения совпадает с направлением скорости движения, если модуль скорости увеличивается, ускорение направлено противоположно скорости движения, если модуль скорости уменьшается.

6. Преобразовав формулу ускорения, можно получить выражение для скорости тела при равноускоренном движении: \( \vec=\vec_0+\vect \) . Если начальная скорость тела ​ \( v_0=0 \) ​, то \( \vec = \vect \) .

Чтобы определить значение скорости равноускоренного движения в любой момент времени, следует записать уравнение для проекции скорости на ось ОХ. Оно имеет вид: \( v_x = v_ <0x>+ a_xt \) ; если \( v_<0x>=0 \) , то \( v_x = a_xt \) .

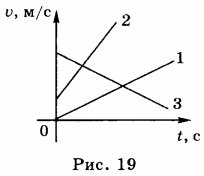
7. Как видно из формулы скорости равноускоренного движения, она линейно зависит от времени. Графиком зависимости модуля скорости от времени является прямая, составляющая некоторый угол с осью абсцисс (осью времени). На рисунке 19 приведены графики зависимости модуля скорости от времени.

График 1 соответствует движению без начальной скорости с ускорением, направленным так же, как и скорость; график 2 — движению с начальной скоростью \( v_ <02>\) и с ускорением, направленным так же, как и скорость; график 3 — движению с начальной скоростью \( v_ <03>\) и с ускорением, направленным в сторону, противоположную направлению скорости.

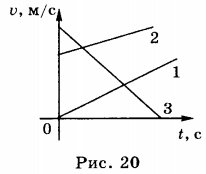
8. На рисунке приведены графики зависимости проекции скорости равноускоренного движения от времени (рис. 20).

График 1 соответствует движению без начальной скорости с ускорением, направленным вдоль положительного направления оси X; график 2 — движению с начальной скоростью \( v_ <02>\) , с ускорением и скоростью, направленными вдоль положительного направления оси X; график 3 — движению с начальной скоростью \( v_ <03>\) : до момента времени \( t_0 \) направление скорости совпадает с положительным направлением оси X, ускорение направлено в противоположную сторону. В момент времени \( t_0 \) скорость равна нулю, а затем и скорость, и ускорение направлены в сторону, противоположную положительному направлению оси X.

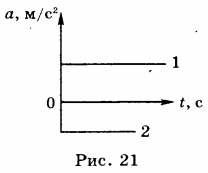
9. На рисунке 21 приведены графики зависимости проекции ускорения равноускоренного движения от времени.

График 1 соответствует движению, проекция ускорения которого положительна, график 2 — движению, проекция ускорения которого отрицательна.

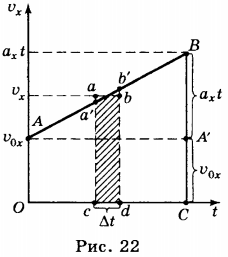
10. Формулу перемещения тела при равноускоренном движении можно получить, используя график зависимости проекции скорости этого движения от времени (рис. 22).

Выделим на графике малый участок ​ \( ab \) ​ и опустим перпендикуляры из точек​ \( a \) ​ и ​ \( b \) ​ на ось абсцисс. Если промежуток времени ​ \( \Delta\) ​, соответствующий участку ​ \( cd \) ​ на оси абсцисс мал, то можно считать, что скорость в течение этого промежутка времени не изменяется и тело движется равномерно. В этом случае фигура ​ \( cabd \) ​ мало отличается от прямоугольника и её площадь численно равна проекции перемещения тела за время, соответствующее отрезку ​ \( cd \) ​.

На такие полоски можно разбить всю фигуру ОАВС, и её площадь равна сумме площадей всех полосок. Следовательно, проекция перемещения тела за время ​ \( t \) ​ численно равна площади трапеции ОАВС. Площадь трапеции равна произведению полусуммы её оснований на высоту: ​ \( S_x= \frac<1><2>(OA+BC)OC \) ​.

Как видно из рисунка, ​ \( OA=v_<0x>,BC=v_x,OC=t \) ​. Отсюда следует, что проекция перемещения выражается формулой \( S_x= \frac<1><2>(v_<0x>+v_x)t \) . Так как \( v_x = v_ <0x>+ a_ \) , то \( S_x= \frac<1><2>(2v_ <0x>+ a_xt)t \) , отсюда \( S_x=v_<0x>t+ \frac <2>\) . Если начальная скорость равна нулю, то формула имеет вид \( S_x=\frac <2>\) . Проекция перемещения равна разности координат \( S_x=x-x_0 \) , поэтому: \( x-x_0=v_<0x>t+\frac <2>\) , или \( x=x_<0x>+v_<0x>t+\frac <2>\) .

Полученная формула позволяет определить положение (координату) тела в любой момент времени, если известны начальная скорость, начальная координата и ускорение.

11. На практике часто используют формулу или \( v^2_x-v^2_<0x>=2a_xs_x \) , или \( v^2-v^2_<0>=2as \) .

Если начальная скорость тела равна нулю, то: ​ \( v^2_x=2a_xs_x \) ​.

Полученная формула позволяет рассчитать тормозной путь транспортных средств, т.е. путь, который проезжает, например, автомобиль до полной остановки. При некотором ускорении движения, которое зависит от массы автомобиля и силы тяги двигателя, тормозной путь тем больше, чем больше начальная скорость автомобиля.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

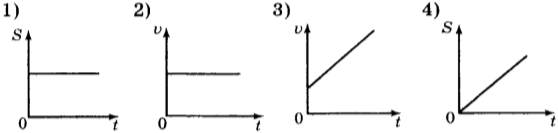
1. Hа рисунке приведены графики зависимости пути и скорости тела от времени. Какой график соответствует равноускоренному движению?

2. Автомобиль, начав двигаться из состояния покоя но прямолинейной дороге, за 10 с приобрел скорость 20 м/с. Чему равно ускорение автомобиля?

1) 200 м/с 2
2) 20 м/с 2
3) 2 м/с 2
4) 0,5 м/с 2

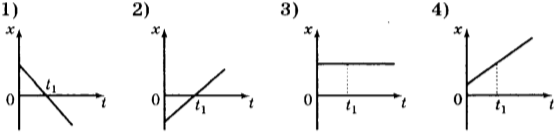
3. На рисунках представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси ​ \( Оx \) ​. У какого из тел в момент времени ​ \( t_1 \) ​ скорость движения равна нулю?

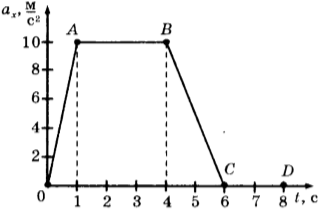
4. На рисунке представлен график зависимости проекции ускорения от времени для тела, движущегося прямолинейно вдоль оси ​ \( Оx \) ​.

Равноускоренному движению соответствует участок

1) только ОА
2) только АВ
3) только ОА и ВС
4) только CD

5. При изучении равноускоренного движения измеряли путь, пройденный телом из состояния покоя за последовательные равные промежутки времени (за первую секунду, за вторую секунду и т.д.). Полученные данные приведены в таблице.

Чему равен путь, пройденный телом за третью секунду?

1) 4 м
2) 4,5 м
3) 5 м
4) 9 м

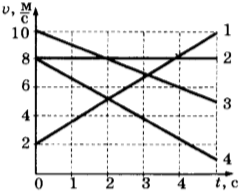
6. На рисунке представлены графики зависимости скорости движения от времени для четырёх тел. Тела движутся по прямой.

Для какого(-их) из тел — 1, 2, 3 или 4 — вектор ускорения направлен противоположно вектору скорости?

1) только 1
2) только 2
3) только 4
4) 3 и 4

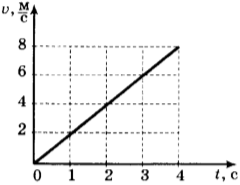
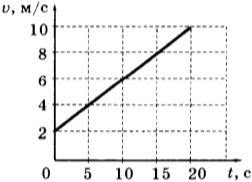
7. Используя график зависимости скорости движения тела от времени, определите его ускорение.

1) 1 м/с 2
2) -1 м/с 2
3) 2 м/с 2
4) -2 м/с 2

8. При изучении равноускоренного движения измеряли скорость тела в определённые моменты времени. Полученные данные, приведены в таблице. Чему равна скорость тела в момент времени 3 с?

1) 0 м/с
2) 2 м/с
3) 4 м/с
4) 14 м/с

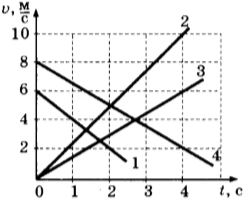
9. На рисунке приведены графики зависимости скорости движения четырёх тел от времени. Ускорение какого из тел равно -1,5 м/с?

10. Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 30-й секунды. Считать, что характер движения тела не изменился.

1) 14 м/с
2) 20 м/с
3) 62 м/с
4) 69,5 м/с

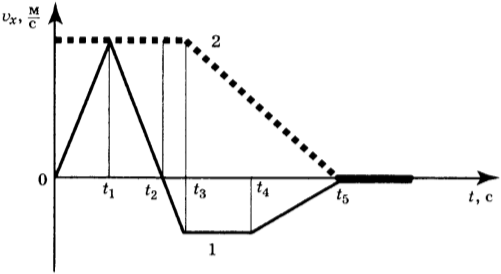
11. Два тела движутся по оси ​ \( Оx \) ​. На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) В промежутке времени ​ \( t_3-t_5 \) ​ тело 2 движется равноускоренно.
2) К моменту времени ​ \( t_2 \) ​ от начала движения тела прошли одинаковые пути.
3) В промежутке времени ​ \( 0-t_3 \) ​ тело 2 находится в покое.
4) В момент времени ​ \( t_5 \) ​ тело 1 останавливается.
5) В промежутке времени ​ \( t_3-t_4 \) ​ ускорение ​ \( a_x \) ​ тела 1 отрицательно.

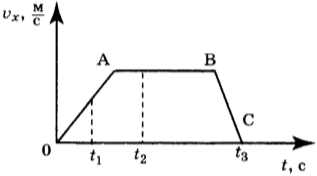
12. На рисунке представлен график зависимости проекции скорости от времени для тела, движущегося вдоль оси Ох.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) Участок ОА соответствует ускоренному движению тела.
2) Участок АВ соответствует состоянию покоя тела.
3) В момент времени ​ \( t_1 \) ​ тело имело максимальное по модулю ускорение.
4) Момент времени ​ \( t_3 \) ​ соответствует остановке тела.
5) В момент времени ​ \( t_2 \) ​ тело имело максимальное по модулю ускорение.

Часть 2

13. Зависимость координаты от времени для некоторого тела описывается уравнением ​ \( x=12t-t^2 \) ​. В какой момент времени скорость движения равна нулю?

Равноускоренное движение: формулы, примеры

Равноускоренное движение

Равноускоренное движение — это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение — частный случай равноускоренного движения с ускорением, равным нулю.

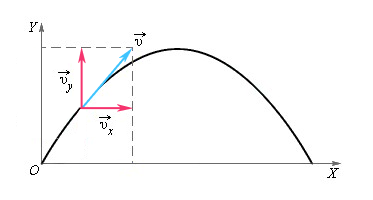
Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.

В любой точке траектории на тело действует ускорение свободного падения g → , которое не меняется по величине и всегда направлено в одну сторону.

Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y — равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.

Формулы для равноускоренного движения

Формула для скорости при равноускоренном движении:

Здесь v 0 — начальная скорость тела, a = c o n s t — ускорение.

Покажем на графике, что при равноускоренном движении зависимость v ( t ) имеет вид прямой линии.

​​​​​​​

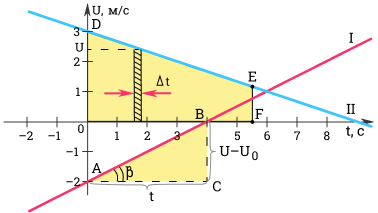
Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.

a = v — v 0 t = B C A C

Чем больше угол β , тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v 0 = — 2 м с ; a = 0 , 5 м с 2 .

Для второго графика: v 0 = 3 м с ; a = — 1 3 м с 2 .

По данному графику можно также вычислить перемещение тела за время t . Как это сделать?

Выделим на графике малый отрезок времени ∆ t . Будем считать, что он настолько мал, что движение за время ∆ t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆ t . Тогда, перемещение ∆ s за время ∆ t будет равно ∆ s = v ∆ t .

Разобьем все время t на бесконечно малые промежутки ∆ t . Перемещение s за время t равно площади трапеции O D E F .

s = O D + E F 2 O F = v 0 + v 2 t = 2 v 0 + ( v — v 0 ) 2 t .

Мы знаем, что v — v 0 = a t , поэтому окончательная формула для перемещения тела примет вид:

s = v 0 t + a t 2 2

Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.

Закон равноускоренного движения

y = y 0 + v 0 t + a t 2 2 .

Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения — нахождение координаты при заданных значениях начальной и конечной скоростей и ускорения.

Исключая из записанных выше уравнений t и решая их, получаем:

s = v 2 — v 0 2 2 a .

По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:

v = v 0 2 + 2 a s .

При v 0 = 0 s = v 2 2 a и v = 2 a s

Величины v , v 0 , a , y 0 , s , входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.

Графическое представление равноускоренного прямолинейного движения. Перемещение при равноускоренном движении

1.9. Графическое представление равноускоренного прямолинейного движения.

Перемещение при равноускоренном движении.

Многие физические величины, описывающие движения тел, с течением времени изменяются. Поэтому для большей наглядности описания движение часто изображают графически.

Покажем, как графически изображаются зависимости от времени кинематических величин, описывающих прямолинейное равноускоренное движения.

Равноускоренное прямолинейное движение — это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т. е. это движение с постоянным по модулю и направлению ускорением.

a=const — уравнение ускорения. Т. е а имеет численное значение, которое не изменяется со временем.

По определению ускорения

Отсюда мы уже нашли уравнения для зависимости скорости от времени: v = v0 + at.

Посмотрим, как это уравнение можно использовать для графического представления равноускоренного движения.

Изобразим графически зависимости кинематических величин от времени для трех тел

.

1 тело движется вдоль оси 0Х, при этом увеличивает свою скорость (вектор ускорения а сонаправленн с вектором скорости v). vx >0, ах > 0

2 тело движется вдоль оси 0Х, при этом уменьшает свою скорость (вектор ускорения а не сонаправленн с вектором скорости v). vx >0, ах 0

Ускорение по определению величина постоянная. Тогда для представленной ситуации график зависимости ускорения от времени a(t) будет иметь вид:

Из графика ускорения можно определить как изменялась скорость – увеличивалась или уменьшалась и на какое численное значение изменилась скорость и у какого тела скорость больше изменилась.

Если сравнить зависимость координаты от времени при равномерном движении и зависимость проекции скорости от времени при равноускоренном движении, можно увидеть, что эти зависимости одинаковы:

Это значит, что и графики зависимостей имеют одинаковый вид.

Для построения этого графика на оси абсцисс откладывают время движения, а на оси ординат — скорость (проекцию скорости) тела. В равноускоренном движении скорость тела с течением времени изменяется.

Перемещение при равноускоренном движении.

При равноускоренном прямолинейном движении скорость тела определяется формулой

В этой формуле υ0 – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. ).

По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. для графика I. Ускорение численно равно отношению сторон треугольника ABC:

Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.

Для графика I: υ0 = –2 м/с, a = 1/2 м/с2.

Для графика II: υ0 = 3 м/с, a = –1/3 м/с2.

График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной полоски (рис. ). Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены для графика II на рис. 1.4.2. Время t принято равным 5,5 с.

Так как υ – υ0 = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:

Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y0 прибавить перемещение за время t:

Так как υ – υ0 = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:

Для нахождения координаты x тела в любой момент времени t нужно к начальной координате x0 прибавить перемещение за время t:

При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ0 и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде

Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ0, ускорение a и перемещение s:

Если начальная скорость υ0 равна нулю, эти формулы принимают вид

Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ0, υ, s, a, y0 являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.

Пример решения задачи:

Петя съезжает со склона горы из состояния покоя с ускорением 0,5 м/с2 за 20 с и дальше движется по горизонтальному участку. Проехав 40 м, он врезается в зазевавщегося Васю и падает в сугроб, снизив свою скорость до 0м/с. С каким ускорением двигался Петя по горизонтальной поверхности до сугроба? Какова длина склона горы, с которой так неудачно съехал Петя?

Движение Пети состоит из двух этапов: на первом этапе, спускаясь со склона горы, он движется с возрастающей по модулю скоростью; на втором этапе при движении по горизонтальной поверхности его скорость уменьшается до нуля (столкнулся с Васей). Величины, относящиеся к первому этапу движения, запишем с индексом 1, а ко второму этапу с индексом 2.

Уравнение для скорости Пети в конце спуска с горы:

В проекциях на ось X получим:

Запишем уравнение, связывающее проекции скорости, ускорения и перемещения Пети на первом этапе движения:

или т. к. Петя ехал с самого верха горки с начальной скоростью V01=0

(на месте Пети, я бы поостереглась ездить с таких высоких горок)

Учитывая, что начальная скорость Пети на этом 2 этапе движения равна его конечной скорости на первом этапе:

v02x = v1x, v2x = 0, где v1 – скорость с которой Петя достиг подножия горки и начал двигаться к Васе. V2x — скорость Пети в сугробе.

Используем уравнение и найдем скорость v1

На горизонтальним участе дороги путь Пети рамен:

НО. целесообразнее воспользоваться другим уравнением, т. к. нам не известно время жвижения Пети до Васи t2

Ускорение получиться отрицательным – это значит, что Петя очень старался затормозить не об Васю, а несколько раньше.

II уровень. Письменно решить задачи.

1. Поезд метро, отходя от станции, может развить скорость 72 км/ч за 20 с. Определить с каким ускорением удаляется от вас сумка, забытая в вагоне метро. Какой путь при этом она проедет?

2. Велосипедист, движущийся со скоростью 3 м/с, начинает спускаться с горы с ускорением 0,8 м/с2. Найдите длину го­ры, если спуск занял 6 с.

3. Начав торможение с ускорением 0,5 м/с2, поезд прошел до остановки 225 м. Какова была его скорость перед началом торможения?

4. Начав двигаться, футбольный мяч достиг скорости 50 м/с, пройдя путь 50 м и врезался в окно. Определите время, за которое мяч прошел этот путь, и ускорение, с которым он двигался.

5. Время реакции соседа дяди Олега = 1,5 мин, за это время он сообразит, что случилось с его окном и успеет выбежать во двор. Определите какую скорость должны развить юные футболисты, что бы радостные владельцы окна их не догнали, если до своего подъезда им нужно бежать 350 м.

6. Два велосипедиста еду навстречу друг другу. Первый, имея скорость 36 км/ч, начал подниматься в гору с ускоре­нием 0,2 м/с2, а второй, имея скорость 9 км/ч, стал спус­каться с горы с ускорением 0,2 м/с2. Через сколько времени и в каком месте они столкнуться из-за своей рассеянности, если длина горы 100 м?