Равноускоренное прямолинейное движение кинематические уравнения графическое представление

Конспект по физике по теме «Равноускоренное прямолинейное движение» (10 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Равноускоренное движение. Графическое представление равнопеременного движения .

Прямолинейное равнопеременное движение – движение материальной точки, при котором скорость материальной точки за любые равные промежутки времени изменяется одинаково, а ее траекторией является прямая линия.

1) ; т .к. равноускоренное , т.к. прямолинейное , значит

Равноускоренное прямолинейное движение – движение с постоянным по величине и направлению ускорением.

2) , так как , значит .

Равноускоренное прямолинейное движение – движение, при котором скорость за любые равные промежутки времени изменяется одинаково.

Существует три способа описания механического движения. Рассмотрим их применительно к равнопеременному прямолинейному движению:

1) Словесный. Зададим кинематическую картину движения. Выберем тело отсчета и свяжем с ним систему координат. Т.к. движение прямолинейное, то достаточно одномерной системы координат OX . Установим часы. Укажем направления кинематических величин, характеризующих движение.

Пусть материальная точка начинает движение в точке с координатой х₀, а через время t оказывается в точке с координатой х. Вектор перемещения соединит эти точки. Скорость изменяется по величине. Нормальная составляющая ускорения равна нулю, тангенциальная составляющая ускорения постоянна.

Различают два вида равнопеременного прямолинейного движения

Равноускоренное прямолинейное движение

Равнозамедленное прямолинейное движение

ККД

ККД

ККД

ККД

при равноускоренном движении знаки проекций ускорений и начальной скорости одинаковые.

при равнозамедленном движении знаки проекций ускорений и начальной скорости разные.

2) Аналитический. Зададим уравнения движения (уравнения зависимости кинематических величин от времени).

При равнопеременном движении ускорение постоянно и по величине и по направлению. Проекция скорости на ось ОХ может быть как положительной, так и отрицательной, в зависимости от направления вектора изменения скорости.

При равнопеременном движении скорость можно выразить из определения ускорения: . Для проекции скорости на ось ОХ можно получить аналогичное уравнение: . При равнопеременном прямолинейном движении скорость точки и ее проекции на ось изменяются со временем по линейному закону.

Известно, что модуль вектора перемещения тела численно равен площади фигуры, заключенный между графиком скорости, осью Ot и перпендикулярами к этой оси, восстановленными из точек, соответствующих моментам начала и конца наблюдения. Построим этот график согласно полученному ранее закону:

Найдем площадь фигуры под графиком :

Или аналогичное уравнение в векторном виде:

Также можно вывести формулу расчета перемещения без учета времени:

;

Если =0, то

Обратимся к ККД. . Воспользуемся связью между радиус-вектором и вектором перемещения: . Получим

Существует связь между проекцией перемещения на ось и координатами начала и конца движения тела: Следовательно,

Путь всегда положителен и равен модулю перемещения (так как движение прямолинейное): .

Система векторных уравнений :

Система скалярных уравнений :

3) Графический. Зададим графики зависимости кинематических величин от времени (согласно полученным уравнениям).

Найдем площадь фигуры под графиком модуля ускорения: – изменение скорости.

Изменение скорости за промежуток времени t численно равно площади фигуры, ограниченной графиком ускорения, осью Ot и перпендикулярами к этой оси, восстановленными из точек, соответствующих моментам начала и конца наблюдения (площади фигуры ограниченной графиком ускорения).

По графику а_х( t ) можно:

1) определить ускорение в любой момент времени и по величине и по направлению;

2) найти изменение скорости тела и по величине и по направлению;

3) если , то можно найти скорость тела как площадь фигуры ограниченной графиком проекции ускорения.

По графику V_x ( t ) можно:

1) Найти значение скорости в любой момент времени по величине и направлению;

2) Определить начальную скорость как точку пересечения графика V_x ( t ) с осью ОХ;

3) Определить момент времени, когда скорость станет равной нулю – точка пересечения графика V_x ( t ) с осью t ;

4) Проекцию перемещения на ось ОХ как площадь фигуры, ограниченной графиком скорости;

5) Найдем tgα = -> Модуль вектора ускорения тела численно равен тангенсу угла наклона графика V_x ( t ) к оси времени. Чем больше угол наклона графика к оси времени, тем больше ускорение. Если ускорение одинаково по модулю, то графики x ( t ) параллельны.

По графику х( t ) можно:

1) Определить начальную координату – точка пересечения графика x ( t ) с осью ОХ;

2) Определить момент времени, когда координата станет равной нулю – точка пересечения графика x ( t ) с осью t ;

3) Найти координату точки в любой момент времени;

4) Определить направление ускорения;

5) Определить наличие или отсутствие начальной скорости.

Графическое представление равноускоренного прямолинейного движения. Перемещение при равноускоренном движении

1.9. Графическое представление равноускоренного прямолинейного движения.

Перемещение при равноускоренном движении.

Многие физические величины, описывающие движения тел, с течением времени изменяются. Поэтому для большей наглядности описания движение часто изображают графически.

Покажем, как графически изображаются зависимости от времени кинематических величин, описывающих прямолинейное равноускоренное движения.

Равноускоренное прямолинейное движение — это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т. е. это движение с постоянным по модулю и направлению ускорением.

a=const — уравнение ускорения. Т. е а имеет численное значение, которое не изменяется со временем.

По определению ускорения

Отсюда мы уже нашли уравнения для зависимости скорости от времени: v = v0 + at.

Посмотрим, как это уравнение можно использовать для графического представления равноускоренного движения.

Изобразим графически зависимости кинематических величин от времени для трех тел

.

1 тело движется вдоль оси 0Х, при этом увеличивает свою скорость (вектор ускорения а сонаправленн с вектором скорости v). vx >0, ах > 0

2 тело движется вдоль оси 0Х, при этом уменьшает свою скорость (вектор ускорения а не сонаправленн с вектором скорости v). vx >0, ах 0

Ускорение по определению величина постоянная. Тогда для представленной ситуации график зависимости ускорения от времени a(t) будет иметь вид:

Из графика ускорения можно определить как изменялась скорость – увеличивалась или уменьшалась и на какое численное значение изменилась скорость и у какого тела скорость больше изменилась.

Если сравнить зависимость координаты от времени при равномерном движении и зависимость проекции скорости от времени при равноускоренном движении, можно увидеть, что эти зависимости одинаковы:

Это значит, что и графики зависимостей имеют одинаковый вид.

Для построения этого графика на оси абсцисс откладывают время движения, а на оси ординат — скорость (проекцию скорости) тела. В равноускоренном движении скорость тела с течением времени изменяется.

Перемещение при равноускоренном движении.

При равноускоренном прямолинейном движении скорость тела определяется формулой

В этой формуле υ0 – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. ).

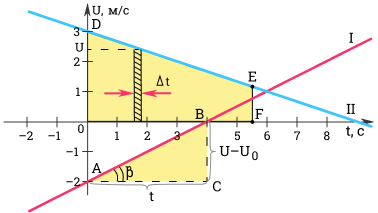
По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. для графика I. Ускорение численно равно отношению сторон треугольника ABC:

Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.

Для графика I: υ0 = –2 м/с, a = 1/2 м/с2.

Для графика II: υ0 = 3 м/с, a = –1/3 м/с2.

График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной полоски (рис. ). Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены для графика II на рис. 1.4.2. Время t принято равным 5,5 с.

Так как υ – υ0 = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:

Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y0 прибавить перемещение за время t:

Так как υ – υ0 = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:

Для нахождения координаты x тела в любой момент времени t нужно к начальной координате x0 прибавить перемещение за время t:

При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ0 и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде

Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ0, ускорение a и перемещение s:

Если начальная скорость υ0 равна нулю, эти формулы принимают вид

Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ0, υ, s, a, y0 являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.

Пример решения задачи:

Петя съезжает со склона горы из состояния покоя с ускорением 0,5 м/с2 за 20 с и дальше движется по горизонтальному участку. Проехав 40 м, он врезается в зазевавщегося Васю и падает в сугроб, снизив свою скорость до 0м/с. С каким ускорением двигался Петя по горизонтальной поверхности до сугроба? Какова длина склона горы, с которой так неудачно съехал Петя?

Движение Пети состоит из двух этапов: на первом этапе, спускаясь со склона горы, он движется с возрастающей по модулю скоростью; на втором этапе при движении по горизонтальной поверхности его скорость уменьшается до нуля (столкнулся с Васей). Величины, относящиеся к первому этапу движения, запишем с индексом 1, а ко второму этапу с индексом 2.

Уравнение для скорости Пети в конце спуска с горы:

В проекциях на ось X получим:

Запишем уравнение, связывающее проекции скорости, ускорения и перемещения Пети на первом этапе движения:

или т. к. Петя ехал с самого верха горки с начальной скоростью V01=0

(на месте Пети, я бы поостереглась ездить с таких высоких горок)

Учитывая, что начальная скорость Пети на этом 2 этапе движения равна его конечной скорости на первом этапе:

v02x = v1x, v2x = 0, где v1 – скорость с которой Петя достиг подножия горки и начал двигаться к Васе. V2x — скорость Пети в сугробе.

Используем уравнение и найдем скорость v1

На горизонтальним участе дороги путь Пети рамен:

НО. целесообразнее воспользоваться другим уравнением, т. к. нам не известно время жвижения Пети до Васи t2

Ускорение получиться отрицательным – это значит, что Петя очень старался затормозить не об Васю, а несколько раньше.

II уровень. Письменно решить задачи.

1. Поезд метро, отходя от станции, может развить скорость 72 км/ч за 20 с. Определить с каким ускорением удаляется от вас сумка, забытая в вагоне метро. Какой путь при этом она проедет?

2. Велосипедист, движущийся со скоростью 3 м/с, начинает спускаться с горы с ускорением 0,8 м/с2. Найдите длину го­ры, если спуск занял 6 с.

3. Начав торможение с ускорением 0,5 м/с2, поезд прошел до остановки 225 м. Какова была его скорость перед началом торможения?

4. Начав двигаться, футбольный мяч достиг скорости 50 м/с, пройдя путь 50 м и врезался в окно. Определите время, за которое мяч прошел этот путь, и ускорение, с которым он двигался.

5. Время реакции соседа дяди Олега = 1,5 мин, за это время он сообразит, что случилось с его окном и успеет выбежать во двор. Определите какую скорость должны развить юные футболисты, что бы радостные владельцы окна их не догнали, если до своего подъезда им нужно бежать 350 м.

6. Два велосипедиста еду навстречу друг другу. Первый, имея скорость 36 км/ч, начал подниматься в гору с ускоре­нием 0,2 м/с2, а второй, имея скорость 9 км/ч, стал спус­каться с горы с ускорением 0,2 м/с2. Через сколько времени и в каком месте они столкнуться из-за своей рассеянности, если длина горы 100 м?

Равноускоренное движение: формулы, примеры

Равноускоренное движение

Равноускоренное движение — это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение — частный случай равноускоренного движения с ускорением, равным нулю.

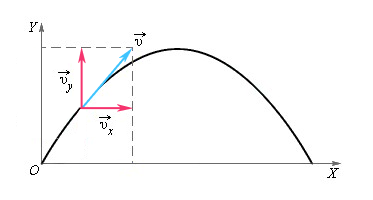
Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.

В любой точке траектории на тело действует ускорение свободного падения g → , которое не меняется по величине и всегда направлено в одну сторону.

Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y — равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.

Формулы для равноускоренного движения

Формула для скорости при равноускоренном движении:

Здесь v 0 — начальная скорость тела, a = c o n s t — ускорение.

Покажем на графике, что при равноускоренном движении зависимость v ( t ) имеет вид прямой линии.

​​​​​​​

Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.

a = v — v 0 t = B C A C

Чем больше угол β , тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v 0 = — 2 м с ; a = 0 , 5 м с 2 .

Для второго графика: v 0 = 3 м с ; a = — 1 3 м с 2 .

По данному графику можно также вычислить перемещение тела за время t . Как это сделать?

Выделим на графике малый отрезок времени ∆ t . Будем считать, что он настолько мал, что движение за время ∆ t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆ t . Тогда, перемещение ∆ s за время ∆ t будет равно ∆ s = v ∆ t .

Разобьем все время t на бесконечно малые промежутки ∆ t . Перемещение s за время t равно площади трапеции O D E F .

s = O D + E F 2 O F = v 0 + v 2 t = 2 v 0 + ( v — v 0 ) 2 t .

Мы знаем, что v — v 0 = a t , поэтому окончательная формула для перемещения тела примет вид:

s = v 0 t + a t 2 2

Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.

Закон равноускоренного движения

y = y 0 + v 0 t + a t 2 2 .

Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения — нахождение координаты при заданных значениях начальной и конечной скоростей и ускорения.

Исключая из записанных выше уравнений t и решая их, получаем:

s = v 2 — v 0 2 2 a .

По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:

v = v 0 2 + 2 a s .

При v 0 = 0 s = v 2 2 a и v = 2 a s

Величины v , v 0 , a , y 0 , s , входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.