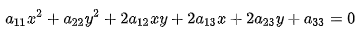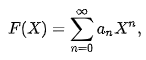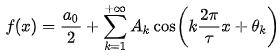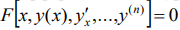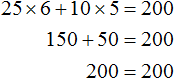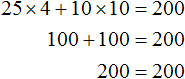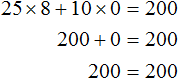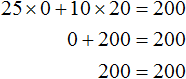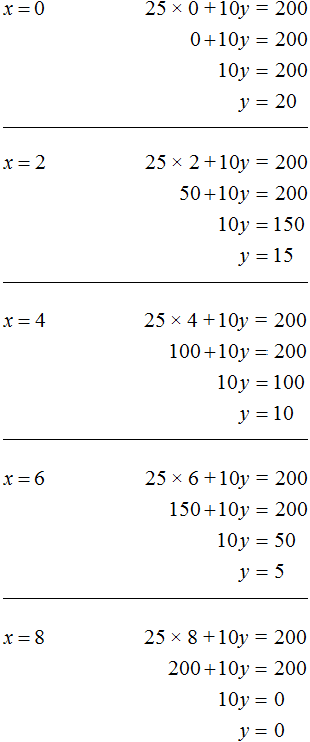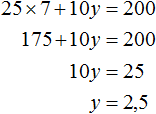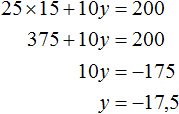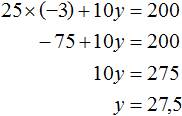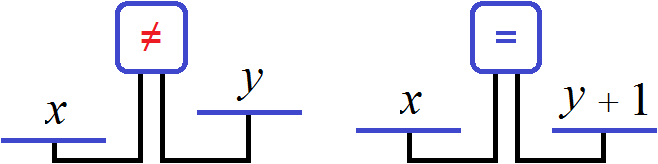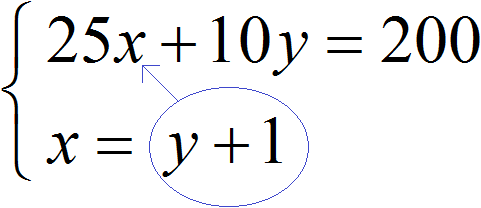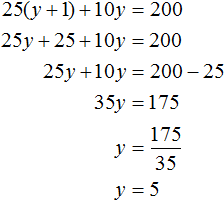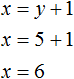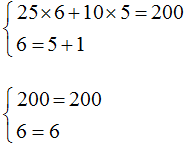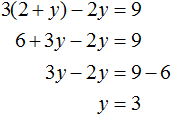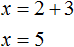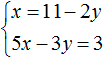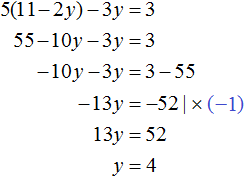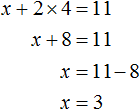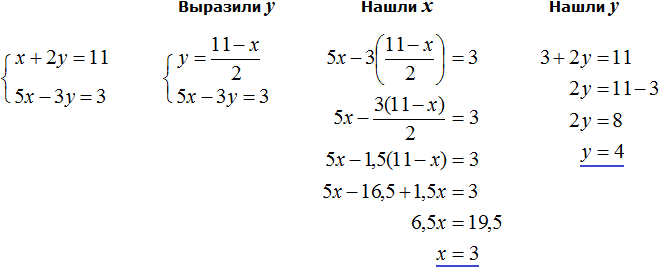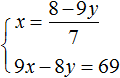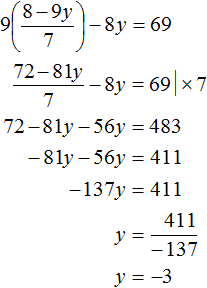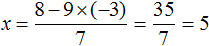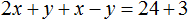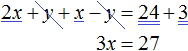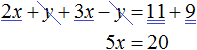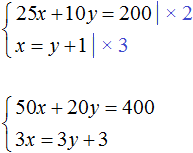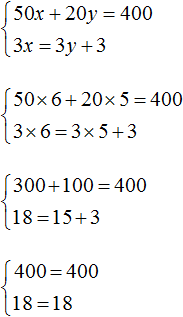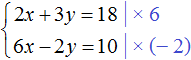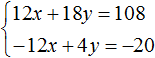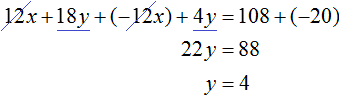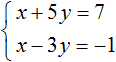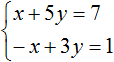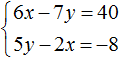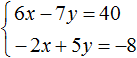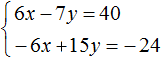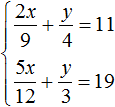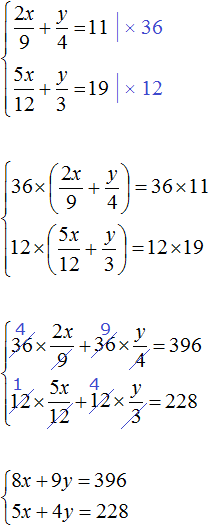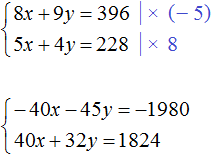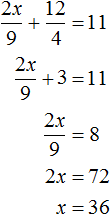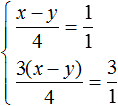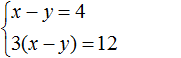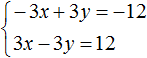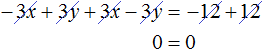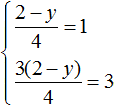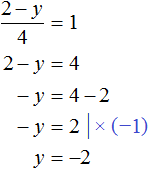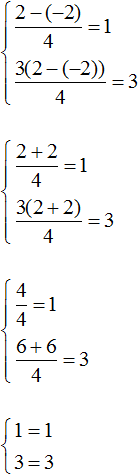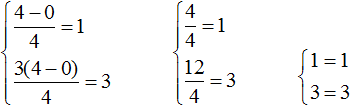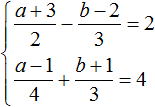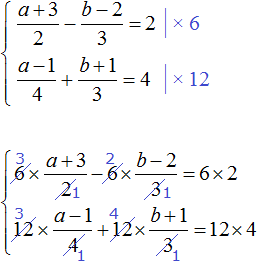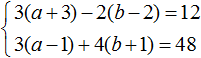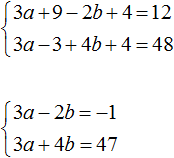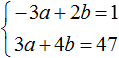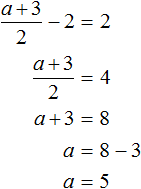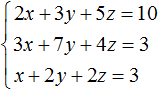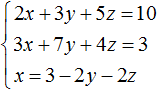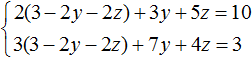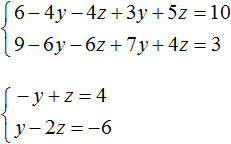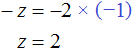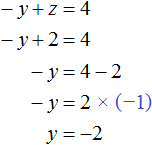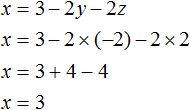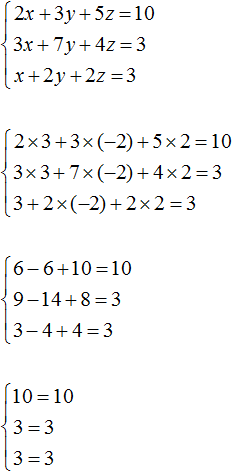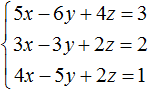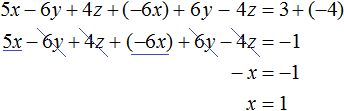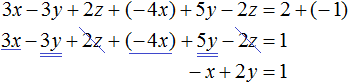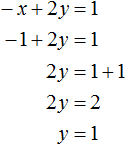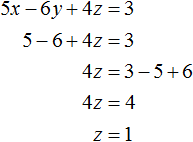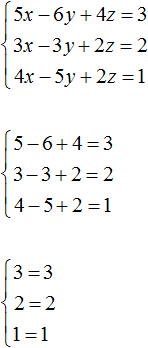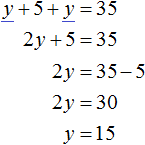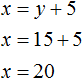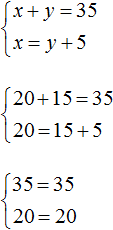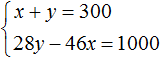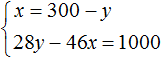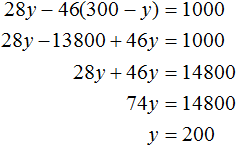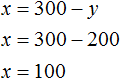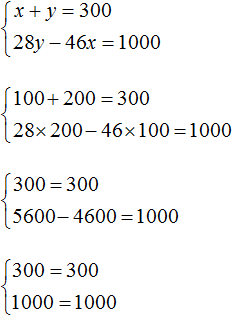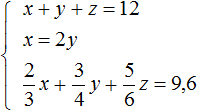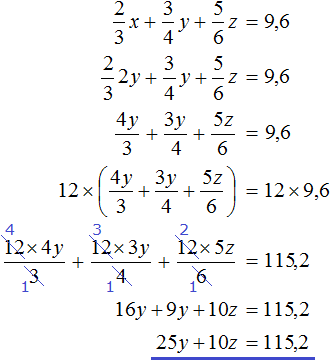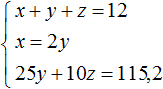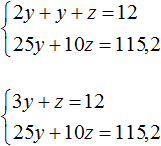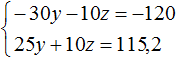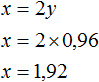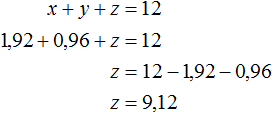Разделы высшей математики система уравнений

Системы уравнений: определение, виды, примеры решения

Статья знакомит с таким понятием, как определение системы уравнений и ее решением. Будут рассмотрены часто встречающиеся случаи решений систем. Приведенные примеры помогут подробно пояснить решение.

Определение системы уравнений

Чтобы перейти к определению системы уравнений, необходимо обратить внимание на два момента: вид записи и ее смысл. Чтобы понять это, нужно подробно остановиться на каждом из видов, тогда сможем прийти к определению систем уравнений.

Например, возьмем два уравнения 2 · x + y = − 3 и x = 5 , после чего объединим фигурной скобкой такого плана:

2 · x + y = — 3 , x = 5 .

Уравнения, объединенные фигурной скобкой, считаются записями систем уравнений. Они задают множества решений уравнений данной системы. Каждое решение должно являться решением всех заданных уравнений.

Другими словами это означает, что любые решения первого уравнения будут решениями всех уравнений, объединенных системой.

Системы уравнений – это некоторое количество уравнений, объединенных фигурной скобкой, имеющих множество решений уравнений, которые одновременно являются решениями для всей системы.

Основные виды систем уравнений

Видов уравнений достаточно много, как систем уравнений. Для того, чтобы было удобно решать и изучать их, подразделяют на группы по определенным характеристикам. Это поможет в рассмотрении систем уравнений отдельных видов.

Для начала уравнения классифицируются по количеству уравнений. Если уравнение одно, то оно является обычным уравнением, если их более, тогда имеем дело с системой, состоящей из двух или более уравнений.

Другая классификация затрагивает число переменных. Когда количество переменных 1 , говорят, что имеем дело с системой уравнений с одной неизвестной, когда 2 – с двумя переменными. Рассмотрим пример

x + y = 5 , 2 · x — 3 · y = 1

Очевидно, что система уравнений включает в себя две переменные х и у .

При записи таких уравнений считается число всех переменных, имеющихся в записи. Их наличие в каждом уравнении необязательно. Хотя бы одно уравнение должно иметь одну переменную. Рассмотрим пример системы уравнений

2 x = 11 , x — 3 · z 2 = 0 , 2 7 · x + y — z = — 3

Данная система имеет 3 переменные х , у , z . Первое уравнение имеет явный х и неявные у и z . Неявные переменные – это переменные, имеющие 0 в коэффициенте. Второе уравнение имеет х и z , а у неявная переменная. Иначе это можно записать таким образом

2 x + 0 · y + 0 · z = 11

А другое уравнение x + 0 · y − 3 · z = 0 .

Третья классификация уравнений – это вид. В школе проходят простые уравнения и системы уравнений, начиная с систем двух линейных уравнений с двумя переменными. Имеется в виду, что система включает в себя 2 линейных уравнения. Для примера рассмотрим

2 · x — y = 1 , x + 2 · y = — 1 и — 3 · x + y = 0 . 5 , x + 2 2 3 · y = 0

Это основные простейшие линейные уравнения. Далее можно столкнуться с системами, содержащими 3 и более неизвестных.

В 9 классе решают уравнения с двумя переменными и нелинейные. В целых уравнениях повышается степень для увеличения сложности. Такие системы называют системами нелинейных уравнений с определенным количеством уравнений и неизвестных. Рассмотрим примеры таких систем

x 2 — 4 · x · y = 1 , x — y = 2 и x = y 3 x · y = — 5

Обе системы с двумя переменными и обе являются нелинейными.

При решении можно встретить дробно-рациональные уравнения. Например

x + y = 3 , 1 x + 1 y = 2 5

Могут называть просто системой уравнений без уточнения, каких именно. Редко уточняют сам вид системы.

Старшие классы переходят к изучению иррациональных, тригонометрических и показательных уравнений. Например,

x + y — x · y = 5 , 2 · x · y = 3 , x + y = 5 · π 2 , sin x + cos 2 y = — 1 , y — log 3 x = 1 , x y = 3 12 .

Высшие учебные заведения изучают и исследуют решения систем линейных алгебраических уравнений (СЛАУ). Левая часть таких уравнений содержит многочлены с первой степенью, а правая – некоторые числа. Отличие от школьных в том, что количество переменных и количество уравнений может быть произвольным, чаще всего несовпадающим.

Решение систем уравнений

Решение системы уравнений с двумя переменными – это пара переменных, которая при подстановке обращает каждое уравнение в верное числовое неравенство, то есть является решением для каждого уравнения данной системы.

К примеру, пара значений х = 5 и у = 2 являются решением системы уравнений x + y = 7 , x — y = 3 . Потому как при подстановке уравнения обращаются в верные числовые неравенства 5 + 2 = 7 и 5 − 2 = 3 . Если подставить пару х = 3 и у = 0 , тогда система не будет решена, так как подстановка не даст верное уравнение, а именно, мы получим 3 + 0 = 7 .

Сформулируем определение для систем, содержащих одну и более переменных.

Решение системы уравнений с одной переменной – это значение переменной, которая является корнем уравнений системы, значит, все уравнения будут обращены в верные числовые равенства.

Рассмотрим на примере системы уравнений с одной переменной t

t 2 = 4 , 5 · ( t + 2 ) = 0

Число — 2 – решение уравнения, так как ( − 2 ) · 2 = 4 , и 5 · ( − 2 + 2 ) = 0 являются верными числовыми равенствами. При t = 1 система не решена, так как при подстановке получим два неверных равенства 12 = 4 и 5 · ( 1 + 2 ) = 0 .

Решение системы с тремя и более переменными называют тройку, четверку и далее значений соответственно, которые обращают все уравнения системы в верные равенства.

Если имеем значения переменных х = 1 , у = 2 , z = 0 , то подставив их в систему уравнений 2 · x = 2 , 5 · y = 10 , x + y + z = 3 , получим 2 · 1 = 2 , 5 · 2 = 10 и 1 + 2 + 0 = 3 . Значит, эти числовые неравенства верные. А значения ( 1 , 0 , 5 ) не будут решением, так как, подставив значения, второе из них будет неверное, как и третье: 5 · 0 = 10 , 1 + 0 + 5 = 3 .

Системы уравнений могут не иметь решений вовсе или иметь бесконечное множество. В этом можно убедиться при углубленном изучении данной тематики. Можно прийти к выводу, что системы уравнений – это пересечение множеств решений всех ее уравнений. Раскроем несколько определений:

Несовместной называют систему уравнений, когда она не имеет решений, в противном случае ее называют совместной.

Неопределенной называют систему, когда она имеет бесконечное множество решений, а определенной при конечном числе решений либо при их отсутствии.

Такие термины редко применяются в школе, так как рассчитаны для программ высших учебных заведений. Знакомство с равносильными системами углубит имеющиеся знания по решению систем уравнений.

Высшая математика

Здравствуйте, на этой странице я собрала полный курс лекций по предмету «высшая математика»

Лекции подготовлены для школьников и студентов любых специальностей и охватывает полный курс предмета « высшая математика ».

В лекциях вы найдёте основные законы, теоремы, формулы и примеры задач с подробным решением.

Высшая математика — курс обучения в средних и высших учебных заведениях, включающий высшую алгебру и математический анализ. Высшая математика включает обычно аналитическую геометрию, элементы высшей и линейной алгебры, дифференциальное и интегральное исчисления, дифференциальные уравнения, теорию множеств, теорию вероятностей и элементы математической статистики. Часто используется в экономике и технике. Является обязательным предметом в российских высших учебных заведениях, за исключением специальностей, в которых различные разделы математики разнесены по разным дисциплинам. wikipedia.org/wiki/Высшая_математика

Введение в высшую математику

Онлайн учебник содержит разделы курса «Высшая математика»: линейная и векторная алгебра, аналитическая геометрия, введение в математический анализ, дифференциальное и интегральное исчисление функции одной переменной, элементы высшей алгебры, соответствующие программе для инженерно-технических специальностей высших учебных заведений. Предназначено для студентов всех специальностей, изучающих дисциплину «Высшая математика».

1. В линейной алгебре изучаются внешне различные объекты: системы линейных уравнений, матрицы, арифметические пространства и линейные операторы в этих пространствах, квадратичные формы. Несмотря на внешнее различие, эти объекты тесно связаны между собой. Целью изучения данной темы и является формирование представлений об этих важных и имеющих многочисленные приложения объектах и их взаимосвязях.
2. В векторной алгебре изучаются геометрические векторы, линейные операции над векторами, скалярное, векторное и смешанное произведения векторов, линейная зависимость и независимость системы векторов, взаимное расположение векторов, понятия базиса и декартовой системы координат.
3. Аналитическая геометрия занимается изучением линий на плоскости и в пространстве и поверхностей в пространстве с использованием понятий вектора и координат. Рассматриваются различные формы уравнений прямой и плоскости, канонические уравнения кривых второго порядка и взаимное расположение прямых и плоскостей.
4. В дифференциальном исчислении функции одной переменной изучаются понятия производной и дифференциала и их применения при исследовании функций.
5. В интегральном исчислении функции одной переменной изучаются понятия первообразной, неопределенного и определенного интеграла, с геометрическими и механическими приложениями определенного интеграла.
6. В теории рядов изучаются понятия решения любых корректно поставленных задач с достаточной для практического использования точностью.
7. В численных (вычислительных) методах изучаются методы и понятия решения математических задач в численном виде.

Элементы линейной алгебры

Линейная алгебра — наиболее важная в приложениях часть алгебры. Первым по времени возникновения вопросом, относящимся к линейной алгебре, была теория линейных уравнений. Развитие последней привело к созданию теории определителей, а затем теории матриц и связанной с ней теории векторных пространств и линейных преобразований в них. В нашем курсе мы будем рассматривать два ключевых аспекта линейной алгебры: теорию матриц и определителей.

Идея введения определителей восходит к известному немецкому математику Готфриду Вильгельму Лейбницу (1646-1716), чей математический гений безграничен и чье имя еще не раз будет упомянуто нами. Лейбниц пришел к определителям при решении систем линейных уравнений в 1678 году. Впервые он сообщил о своем новом методе решения систем в 1693 году в письме к Гийому Лопиталю. В одном из следующих писем Лейбниц писал: «На мой взгляд, это одно из лучших открытий в анализе». К сожалению, Лейбницем в 1700 году был опубликован лишь метод обозначения коэффициентов без каких-либо практических приложений и выводов, поэтому открытие определителей прошло практически незамеченным.

В 1750 году определители были вновь изобретены женевским математиком Крамером, при этом Крамер употребил очень простые и понятные названия — «строки» и «столбцы» определителя, которые сразу же вошли в обиход. Метод Крамера был замечен и очень скоро стал основной частью школьной программы.

Первое исследование, посвященное определителям, было опубликовано французским математиком Вандермондом в 1772 году. Он впервые изложил цельную теорию, ему принадлежат многие классические результаты (например, условие равенства определителя нулю).

Первые полные изложения теории принадлежат Бине и французскому математику Огюстену Коши (1789-1857). Именно Коши ввел в употребление термин «детерминант» (от лат. — «ограничивать», «определять») или «определитель». Бине и Коши одновременно занялись теорией определителей, и, естественно, получили некоторые общие результаты. Во избежание споров о приоритете, они договорились сделать доклады в Академии Наук на одном заседании и опубликовать свои статьи одновременно (1812 год). Коши посвятил теории определителей еще 14 мемуаров. Именно он совсем близко подошел к современному обозначению элементов определителя, употребляя запись . Считают, что именно Коши превратил теорию определителей в самостоятельную дисциплину, оторвав ее от линейных уравнений.

Следующий этап в тридцатых-сороковых годах XIX века составили 30 работ Якоби, среди которых завершающая статья «О построении и свойствах определителей». Якоби ввел в рассмотрение функциональные определители и сделал их методом исследования в математическом анализе. Ему и Коши принадлежит термин «определитель 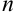-ro порядка». Но на этом математики не остановились: они стали рассматривать бесконечные определители (Котерич в 1770 г., Жюль Пуанкаре (1854-1912) и Кох в 1885).

Ко второй половине XIX века, казалось, не осталось такого раздела математики, куда бы не проникли определители. Но задача, породившая их: в каких случаях система линейных уравнений имеет решения, и если имеет, то сколько их? — еще не была решена. Такое исследование было проведено немецким математиком Леопольдом Кронекером (1823-1891) и изложено им на лекциях в 1864 году. Что касается методов вычисления определителей, то один из них — метод треугольников — придумал страсбургский профессор Саррюс. Другой основан на свойстве определителя, подмеченном Якоби в 1841 году.

Матрицы возникли в середине XIX века одновременно в исследованиях нескольких ученых. Английский математик Артур Кэли (1821-1895) открыл, что систему чисел можно рассматривать как единый математический объект, над которым могут производиться алгебраические действия. Идеи матричного исчисления развивали с 1843 года Кэли, Сильвестр, Лагерр (именно в его статье «Об исчислении линейных систем» матрицы трактуются почти в современной форме), Фробениус (пришел к теории квадратных матриц). Все эти исследования в конце XIX века слились в единую теорию матриц, к изучению которой мы и приступаем.

Понятие матрицы. Операции над матрицами

Матрица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов задает размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Лекции:

Определители. Свойства определителей

Определитель — это скалярная величина, которая может быть вычислена и поставлена в однозначное соответствие любой квадратной матрице.

Лекции:

Обратная матрица. Ранг матрицы

Обратная матрица — это такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

Лекции:

Системы линейных уравнений. Решение систем линейных уравнений по правилу Крамера и методом Гаусса

Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных.

Лекции:

Элементы аналитической геометрии

Геометрия — одна из наиболее древних и ранее других систематизированная ветвь математики. Еще древнегреческие математики изучали различные кривые и подразделяли их на «плоские» (прямая, окружность), «телесные» (определяемые сечением тел — эллипс, парабола, гипербола) и линейные (кривые, определяемые кинематически). Но единых методов решения геометрических задач, связанных с данными кривыми, не существовало. Найти такие методы с целью применения их к изучению важных для практики линий различной формы и была призвана аналитическая геометрия. Аналитическая геометрия позволила применять к решению задач не только геометрические модели, тесно связанные с графическим изображением, но и модели аналитические, позволяющие задать любую линию или поверхность с помощью уравнения.

Главным в становлении аналитической геометрии послужило создание координатного метода. В нем ведущую роль играют вычисления, построения же имеют вспомогательное значение. Создание координатного метода было подготовлено трудами древнегреческих математиков, в особенности Аполлония (3-2 в. до н.э.), заложившего основы теории плоских сечений конуса. Он исследовал их методами алгебры, поэтому может считаться одним из предвестников аналитической геометрии.

Систематическое развитие координатный метод получил в первой половине XVII века в работах французских математиков Пьера Ферма (1601-1665) и Рене Декарта (1596-1650). В 1636 году Ферма написал статью «Введение в изучение плоских и телесных мест». Он выбирал косоугольную систему координат и в ней показывал, что кривая, задающаяся квадратным уравнением, есть коническое сечение — эллипс, парабола или гипербола. Но это произведение долго оставалось в рукописи и не нашло широкого распространения.

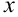
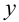
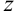
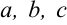
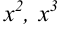
Опубликование в 1637 году «Геометрии» Декарта считается датой рождения аналитической геометрии благодаря использованию координатного метода. В «Геометрии» содержалось много нововведений. Именно Декарт стал обозначать неизвестные последними буквами латинского алфавита (, , ), а коэффициенты — первыми (). Он также ввел привычную нам запись степеней: . Но Декарт и Ферма рассматривали только плоские линии. К систематическому изучению пространственных линий и поверхностей координатный метод был впервые применен Леонардом Эйлером (1707-1783).

Что же касается понятия «вектора», то для математики оно относительно новое. К середине XIX века оно возникает одновременно в трудах нескольких ученых. Первое векторное исчисление на плоскости развил итальянский ученый Беллавитис (1835), в этом исчислении объектами служили отрезки. В это же время получили известность работы Аргана и Весселя о геометрической интерпретации комплексных чисел. Именно Арган обозначил направленный отрезок черточкой над буквой и ввел понятие «модуля» (от лат. 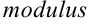— мера).

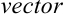
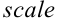
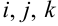
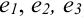
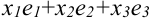
Сам термин «вектор» (от лат. — несущий) впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона (1805-1865) в работах по построению числовых систем, обобщающих комплексные числа. В созданных Гамильтоном кватернионах необходимо было различать скалярную и векторную часть. Поэтому Гамильтону пришлось ввести такие термины, как «скаляр» (от лат. — шкала, лестница), «скалярное произведение». Общепринятые ныне векторы также ввел Гамильтон в 1853 году. Почти одновременно с ним исследования в том же направлении, но с другой точки зрения вел немецкий математик Герман Грассман (1809-1877). Грассман ввел единичные векторы () и представление вектора в виде: .

Англичанин Уильям Клиффорд (1845-1879) сумел объединить эти два подхода в рамках общей теории. А окончательный вид оно приняло в трудах американского физика и математика Джозайи Уилларда Гиббса (1839-1903), который в 1901 году опубликовал обширный учебник по векторному анализу.

Итак, аналитическая геометрия — раздел математики, в котором изучение геометрических объектов (векторов, прямых, плоскостей, кривых, поверхностей) проводится при помощи их аналитических моделей.

Векторы. Операции над векторами. Координаты вектора

Вектор — это направленный отрезок с начальной и конечной точкой. Его можно перемещать параллельно самому себе.

Лекции:

Прямая на плоскости

Прямая на плоскости — это одно из фундаментальных понятий евклидовой геометрии. При систематическом изложении геометрии прямые линии обычно принимаются за одно из исходных (неопределяемых) понятий, их свойства и связь с другими понятиями (например, точки и плоскости) определяются аксиомами геометрии.

Лекции:

Кривые второго порядка

Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:

Лекции:

Основы математического анализа

Математическим анализом называют систему дисциплин, объединенных следующими характерными чертами. Предметом их изучения являются количественные соотношения окружающего мира (в отличие от геометрических дисциплин, занимающихся его пространственными свойствами). Эти соотношения выражаются при помощи чисел, как и в алгебре. Но в алгебре рассматриваются преимущественно постоянные величины (преобразование выражений, уравнения — они характеризуют состояние), а в математическом анализе — переменные величины, характеризующие процессы. В основе изучения зависимости между переменными величинами лежит понятие функции.

Зачатки методов математического анализа можно встретить еще у древнегреческих математиков. Так, Архимед (287-212 гг. до н.э.) при вычислении площадей некоторых фигур и при определении объема шара по существу использовал интегральное исчисление, хотя, естественно, не знал его общих методов. Систематическое развитие эти методы получили в XVII веке. Одним из основателей математического анализа стал английский ученый Исаак Ньютон (1643-1727). Исследования в области механики привели его к проблемам дифференциального и интегрального исчисления. Одновременно с Ньютоном проблемами анализа занимался и немецкий математик Готфрид Вильгельм Лейбниц (1646-1716). Оба этих великих ученых не только завершили создание дифференциального и интегрального исчисления (получившего название анализа бесконечно малых величин), но и заложили основы учения о рядах и дифференциальных уравнениях.

Грандиозные успехи естествознания и математики в последующие три столетия во многом были предопределены великим открытиям Ньютона и Лейбница. В XVIII веке большой вклад в развитие математического анализа внес швейцарский математик Леонард Эйлер (1707-1783), свыше 30 лет проработавший в России. Систематизацией уже имеющихся результатов, а также дальнейшим развитием теории занимались многие французские математики: Жан Даламбер (1717-1783), Жозеф Лагранж (1736-1818), Пьер Лаплас(1749-1827), А.Лежандр (1752-1833), Ж.Фурье (1768-1830). К концу XVIII века был накоплен огромный фактический материал, но он был недостаточно разработан в логическом отношении. Многие понятия ученые воспринимали интуитивно.

Очевидные противоречия привели к критическому пересмотру в XIX веке существующих методов и четкому логическому построению математического анализа. Только в XIX веке были даны строгие определения функции, непрерывности, были уточнены понятия предельного перехода и основанные на нем понятия производной и интеграла. Современное понятие функции сформировалось в первой половине XIX века благодаря исследованиям таких выдающихся математиков, как Николай Иванович Лобачевский (1792-1856), Петер Дирихле (1805-1859) и др. Производная была определена как предел отношения приращения функции к приращению аргумента (французский математик Огюстен Коши (1780-1856)), интеграл — как предельное значение интегральных сумм (немецкий математик Бернхард Риман (1826-1866)). До сих пор математическое образование основывается на этих подходах, хотя в XX веке они получили значительное развитие. Тогда же вошли в употребление термины математика «элементарная» (математика, предшествовавшая рождению математического анализа) и «высшая» (начинается с понятий производной, предела и интеграла).

Одним из важнейших завоеваний математического анализа в XIX веке стало рождение теории аналитических функций и функций комплексного переменного. Следует упомянуть немецкого математика Карла Гаусса (1777-1855), ставшего основателем теории функций комплексного переменного и определившего понятие предела, русских математиков Пафнутия Львовича Чебышева (1821-1866), создателя конструктивной теории функций, Софью Васильевну Ковалевскую (1850-1891), немецкого математика Давида Гильберта (1862-1943). Важнейшие труды, касающиеся стройного логического построения математического анализа, принадлежат немецким математикам Карлу Вейерштрассу (1815-1897), Юлиусу Дедекинду (1831-1916) и Георгу Кантору (1845-1918).

В XX веке, уже на новом уровне, происходит все большее слияние геометрии и математического анализа. Областью приложения анализа становятся кривые и поверхности, расположенные в многомерных пространствах с дополнительной алгебраической структурой. Исследования в области математического анализа продолжаются и в наши дни.

Теория пределов

Понятие предела — одно из основных понятий математического анализа, на котором базируются многие важные определения, в частности, определение производной. Истоки понятия предела следует искать в Древней Греции. Некоторым подобием предельного перехода был метод исчерпывания, изобретенный Евдоксом (ок. 408-355 до н.э.). В работах Архимеда (ок. 287-212 до н.э.) и Евклида (конец IV-III век до н.э.) этот метод дал поразительные результаты. В новое время идеи предела появляются у немецкого астронома и математика Иоганна Кеплера (1571-1630), итальянского математика Бонавентура Кавальери (1598-1647), английского математика Джона Валлиса (1616-1703).

Слово «лимит» (предел) произошло от латинского 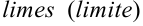— «межа», «граница». Этим словом впервые воспользовался Исаак Ньютон. Однако исторически сложилось так, что точное определение такого ключевого понятия, как предел, и такого важного понятия, как непрерывность, вплоть до конца XVIII века отсутствовали. Соответственно, и многие математические рассуждения содержали пробелы, а иногда были даже ошибочны. Характерный пример — определение непрерывности. Эйлер, Лагранж и даже Фурье (а он работал уже в начале XIX века) называли непрерывной функцию, заданную на области определения одним аналитическим выражением.

Тем самым бурно развивающаяся «новая» математика XVII-XVIII века не отвечала стандартам строгости, привычным для ученых еще со времен древних греков. Интуиция, столь необходимая математикам, существенно опередила логику. Гениальная интуиция таких гигантов, как Ньютон, Лейбниц, Эйлер, помогала им избегать ошибок. Но необходимы были прочные логические основы.

Решительный шаг к созданию прочного фундамента анализа был сделан в 20-е годы XIX века французским математиком Огюстеном Коши (1789-1857), предложившим точное определение пределов функции и последовательности и на их основе доказавшим многие фундаментальные теоремы анализа, в частности теоремы о пределах. Несколько раньше (в 1821 году) определение предела, непрерывности и ряд других замечательных результатов получил чешский математик Бернард Больцано (1781-1848), но его работы стали известны много позднее. После лекций известного немецкого профессора Карла Вейерштрасса (1815-1897), которому принадлежит современное обозначение предела, определение предела по-Коши (на языке 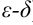) прочно вошло в обиход и используется нами по сей день.

Числовые последовательности

Числовая последовательность — это последовательность чисел. Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.

Лекции:

Предел функции

Предел функции — это такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке. Одно из основных понятий математического анализа.

Лекции:

Непрерывность функции

Непрерывная функция — это функция, которая меняется без мгновенных «скачков» (называемых разрывами), то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции. График непрерывной функции является непрерывной линией.

Лекции:

Дифференциальное исчисление функции одной действительной переменной

Дифференциальное исчисление — один из важнейших разделов математического анализа, в котором изучаются производные и их приложения к исследованию функций.

Дифференциальное исчисление было создано сравнительно недавно, в конце XVII века. К этому понятию одновременно в 70-х-80-х годах XVII века независимо друг от друга подошли два величайших человека своего времени: английский ученый Исаак Ньютон (1643-1727) и немецкий математик Готфрид Вильгельм Лейбниц (1646-1716). Грандиозные успехи естествознания и математики в последующие три столетия были во многом определены великим открытием Ньютона и Лейбница.

Ньютон исходил из необходимости описывать движение тел и развитие различных процессов. Он мыслил как физик — кинематически. Для него суть дифференцирования -нахождение скорости тела в любой момент времени по известному пути. Свое открытие он сделал в 1665-1666 годах, когда Англию постигла эпидемия чумы, и Ньютон вынужден был находиться в своем поместье Вулсторп. Впоследствии он написал работу «Метод флюксий и бесконечных рядов», где метод флюксий — не что иное, как дифференцирование. Но эта работа была опубликована лишь в 1736 году. Сочинения Ньютона по математике увидели свет лишь в XVIII веке, однако кое-что было известно его коллегам из писем. Так, некоторые свои результаты в математическом анализе Ньютон сообщил Лейбницу в 1676 году, когда тот уже сам пришел к открытию дифференциального исчисления.

Подход Лейбница был геометрическим. На него большое впечатление произвели работы Паскаля, в особенности задачи о проведении касательной. В 1765 году им были сделаны первые шаги по созданию нового исчисления: в рукописях Лейбница появляются основные понятия, вводятся операции и символы. Именно Лейбниц ввел термин «дифференциальное исчисление», который с удивительной точностью описывает суть теории. 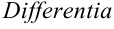по латыни — «разделение», «раздробление». Процесс дифференцирования состоит в замене функции на маленьком участке ее дифференциалом, т.е. кусочком ее касательной. Участку, на котором производится замена, Лейбниц дал название «бесконечно малый». Свои результаты Лейбниц опубликовал лишь в 1684 году в короткой статье из шести страниц «Новый метод максимумов и минимумов, а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления». С этого момента начинается официальная история математического анализа.

Следует отметить, что в предыдущие полвека Блез Паскаль (1623-1662), Пьер Ферма (1601-1665) и другие ученые фактически дали правила разыскания производных многих функций. Ферма предложил правила нахождения экстремумов. Ньютон и Лейбниц завершили это развитие, они разработали аппарат дифференциального исчисления до максимальных пределов, применили дифференциальное исчисление к решению многих задач геометрии и механики.

Исследования Лейбница в значительной степени определили развитие методов анализа в Европе. Среди его последователей — братья Иоганн (1667-1748) и Якоб (1654— 1705) Бернулли, Пьер Вариньон и Гийом де Лопиталь (1661-1704). Именно Лопиталь в 1696 году стал автором первого печатного учебника по дифференциальному исчислению.

Производная функции, нахождение производных различных функций

Производная функции — это понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Лекции:

Геометрический смысл производной. Дифференциал функции

Геометрический смысл производной — это когда численно производная функция в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох.

Лекции:

Производные и дифференциалы высших порядков. Правило Лопиталя

Производные высших порядков — это если функция y=f(x)y=f(x) имеет производную в каждой точке xx своей области определения, то ее производнаяf′(x)f′(x) есть функция от xx. Функция y=f′(x)y=f′(x), в свою очередь, может иметь производную, которую называют производной второго порядка функции y=f(x)y=f(x) (или второй производной) и обозначают символом f′′(x)f′′(x).

Дифференциалы высших порядков — это если функция y=f(x) зависит от переменной x и дифференцируема в точке x. Может оказаться, что в точке xдифференциал dy=f′(x)dx, рассматриваемый как функция от x, есть также дифференцируемая функция. Тогда существует дифференциал от дифференциала d(dy) данной функции, который называется дифференциалом второго порядка функции y=f(x).

Лекции:

Возрастание и убывание, экстремумы функций

Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.

Функция y=f(x) называется убывающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует меньшее значение функции.

Экстремум функции — это называются значения функции в точках максимума и минимума.

Лекции:

Выпуклость графика функции. Точки перегиба

Выпуклая функция — это функция, для которой любой отрезок между двумя любыми точками графика функции в векторном пространстве лежит не ниже соответствующей дуги графика. Эквивалентно, выпуклой является функция, на график которой является выпуклым множеством.

Точка перегиба — точка плоской кривой, в которой её ориентированная кривизна меняет знак. Если кривая является графиком функции, то в этой точке выпуклая часть функции отделяется от вогнутой (то есть вторая производная функции меняет знак).

Лекции:

Асимптоты графика функции

Асимптоты графика функции — это такая прямая, к которой график заданной функции приближается сколько угодно близко, но не пересекает ее.

Лекции:

Общая схема исследования функции и построения графика

В данной лекции мы подведем итог всему ранее изученному материалу. Конечная цель нашего долгого пути — уметь исследовать любую аналитически заданную функцию и строить ее график. Важными звеньями нашего исследования будут исследование функции на экстремумы, определение интервалов монотонности, выпуклости и вогнутости графика, поиск точек перегиба, асимптот графика функции.

Лекция:

Интегральное исчисление функции одной действительной переменной

Интегральное исчисление — один из важнейших разделов математического анализа, тесно связанный с дифференциальным исчислением. Интегральное исчисление возникло из потребностей создать общий метод нахождения площадей фигур и объемов тел.

Истоки интегрального исчисления следует искать в Древней Греции. Евдокс Книдский (ок. 408-355 до н.э.) создал метод исчерпывания, которым пользовался при вычислении площадей криволинейных фигур. Этот метод был усовершенствован Архимедом (ок. 287-212 до н.э.) и позволил ему найти объемы шара и эллипсоида, площадь сегмента параболы и т.д. Архимед предвосхитил многое идеи интегрального исчисления, но потребовалось более полутора тысяч лет, прежде чем эти идеи нашли четкое выражение и были доведены до уровня исследования.

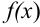
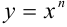
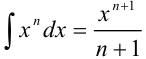
Математики XVII столетия, получившие многие новые результаты, учились на трудах Архимеда. Немецкий математик и астроном Иоганн Кеплер (1571-1630) правильно вычислил ряд площадей (криволинейную трапецию он представлял составленной из бесконечного числа вертикальных отрезков длиной ) и объемов (тело разрезалось на бесконечно тонкие пластинки). Эти исследования продолжили итальянские математики Бонавентура Кавальери (1598-1647) и Эванджелиста Торричелли (1608-1647). Французский математик Пьер Ферма (1601-1665) уже в 1629 году умел находить площадь под кривой , т.е. по существу вывел формулу . Кеплер при выводе своих знаменитых законов движения планет фактически опирался на идею приближенного интегрирования.

Первым человеком, сумевшим обнаружить связь между вычислением площади под кривой и задачей о проведении касательной, был учитель Ньютона, английский математик Исаак Барроу (1630-1677). Однако при всей значимости результатов, полученных математиками XVII века, исчисления еще не было. Нужно было выделить общие идеи, лежащие в основе многих частных задач, установить связь интегрирования и дифференцирования. Это сделали Исаак Ньютон и Готфрид Лейбниц, открывшие независимо друг от друга формулу, известную нам как формула Ньютона-Лейбница. Тем самым окончательно сформировался общий метод. Предстояло еще научиться находить первообразные многих функций, дать логические основы нового исчисления. Но главное уже было сделано: дифференциальное и интегральное исчисление создано.

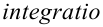
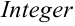
Термин «интегральное исчисление» возник в результате переписки Лейбница и И.Бернулли. Вероятно, оно происходит от лат. — «восстановление». Действительно, при интегрировании мы «восстанавливаем» функцию по известной производной. Существует и другая точка зрения. по-латыни — «целый», интегрирование — процесс объединения в целое малых элементов, из которых составлена фигура (при нахождении площади, объема).

Методы математического анализа активно развивались в XVIII веке. В первую очередь следует назвать Леонарда Эйлера (1707-1783), завершившего систематическое исследование интегрирования элементарных функций. Большое значение имели результаты русских ученых Пафнутия Львовича Чебышева (1828-1894), доказавшего, что существуют интегралы, невыразимые через элементарные функции, а также Михаила Васильевича Остроградского (1801-1862) и В.Я.Буняковского (1804-1889).

Строгое изложение теории интегралов появилось только в XIX веке. Решение этой задачи связано с именем Огюстена Коши (1789-1857). Теорию интегралов Коши обобщил крупнейший немецкий математик Бернхард Риман (1826-1866). Ответы на многие вопросы, связанные с существованием площадей и объемов фигур, были получены создателями теории меры (обобщение понятие площади и объема) Камилем Жорданом (1838-1922) и Анри Лебегом (1875-1941).

Неопределенный интеграл и его свойства. Таблица основных интегралов

Неопределённый интеграл — это совокупность всех первообразных данной функции.

Лекции:

Основные методы интегрирования неопределённых интегралов

Непосредственное интегрирование — это метод, при котором интеграл, путём тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла, приводится к одному или нескольким интегралам элементарных функций.

Интегралы от некоторых сложных функций — это интегралы, которые нельзя вычислить, используя таблицу интегралов.

Метод интегрирования подстановкой — это метод заключается во введении новой переменной интегрирования. При этом, заданный интеграл приводится к интегралу элементарной функции, или к нему сводящемуся.

Метод интегрирования по частям — это нахождение данного интеграла с помощью формулы интегрирования к нахождению другого интеграла. Смысл формулы интегрирования по частям состоит в том, чтобы в результате её применения новый интеграл оказался табличным или хотя бы стал проще первоначального.

Лекции:

Интегрирование рациональных и иррациональных функций. Универсальная подстановка

Рациональная функция — это функция, которая может быть представлена в виде дроби, числителем и знаменателем которой являются многочлены. К этому виду может быть приведено любое рациональное выражение. , то есть алгебраическое выражение, без радикалов.

Иррациональная функция — это те, которые содержат в себе аргумент под знаком корня (радикала).

Лекции:

Определенный интеграл

Определённый интеграл — это одно из основных понятий математического анализа, один из видов интеграла. Определённый интеграл является числом, равным пределу сумм особого вида (интегральных сумм).

Лекции:

Методы вычисления определенного интеграла

1. Формула Ньютона – Лейбница
2. Замена переменной в определенном интеграле
3. Интегрирование по частям в определенном интеграле

Лекции:

Приложения определенного интеграла в геометрии

Основными геометрическими приложениями определенного интеграла являются: вычисление площади плоской фигуры, вычисление объемов тел вращения вокруг осей координат и вычисление длины дуги плоской кривой.

Лекции:

Несобственные интегралы

Несобственный интеграл — это определённый интеграл, если при решении выполняется, по крайней мере, одно из следующих условий: Область интегрирования является бесконечной. Например, является бесконечным промежутком [a,+ ∞ ). Функция f(x) является неограниченной в окрестности некоторых точек области интегрирования.

Лекции:

Дифференциальное исчисление функции нескольких действительных переменных

Дифференциальное исчисление — это раздел математического анализа, в котором изучаются понятия производной и дифференциала и способы их применения к исследованию функций.

Функции нескольких действительных переменных. Предел и непрерывность

Переменная величина z называется функцией двух переменных величин х и у, если каждой паре допустимых значений х и у соответствует единственное значение z.

Лекции:

Частные производные. Дифференциал функции нескольких действительных переменных

Частная производная — это предел отношения приращения функции по выбранной переменной к приращению этой переменной, при стремлении этого приращения к нулю. В математическом анализе частная производная — одно из обобщений понятия производной на случай функции нескольких переменных.

Дифференциалом функции — это сумму произведений частных производных этой функции на приращения соответствующих независимых переменных.

Лекции:

Частные производные и дифференциалы высших порядков функции нескольких переменных

При вычислении дифференциалов высших порядков очень важно запомнить, что величина dx не зависит от x , то есть относительно переменной дифференцирования является константой, поэтому при дифференцировании по x величину dx следует рассматривать как постоянный множитель.

Лекции:

Интегральное исчисление функции нескольких действительных переменных

Интегральное исчисление — это раздел математического анализа, в котором изучаются понятия интеграла, его свойства и методы вычислений.

Двойные интегралы и их свойства

Двойные интегралы — это обобщение понятия определённого интеграла для функции двух переменных, заданной как z = f(x, y).

Лекции:

Сведение двойных интегралов к повторным в случае областей i и ii типа

Эффективным способом вычисления двойных интегралов является сведение их к однократным интегралам.

Лекции:

Приложение двойного интеграла к вычислению объемов геометрических тел

• Геометрический смысл двойного интеграла
• Вычисление объемов геометрических тел с помощью двойного интеграла

Лекции:

Приложение двойного интеграла к вычислению площадей плоских фигур

• Геометрический смысл двойного интеграла от единичной функции.
• Вычисление площадей плоских фигур с помощью двойного интеграла

Лекции:

Теория рядов

Ряд — это называемый также бесконечная сумма, одно из центральных понятий математического анализа. В простейшем случае ряд записывается как бесконечная сумма чисел.

Определение числового ряда. Свойства рядов. Необходимый признак сходимости

Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).

Лекции:

Признаки сравнения, Даламбера, Коши и интегральных положительных рядов

Признак д’Аламбера — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.

Признак Коши — признак сходимости числового ряда.

Лекции:

Рассмотренные достаточные признаки позволяют исследовать на сходимость фактически любой положительный числовой ряд. Только практика поможет приобрести необходимые навыки исследования и довести их до совершенства.

Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость

Знакочередующийся ряд — это математический ряд, члены которого попеременно принимают значения противоположных знаков.

Признак Лейбница — это признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем.

Абсолютная и условная сходимость — это ряд с действительными или комплексными членами ∞∑n=1an, называется абсолютно сходящимся, если сходится ряд ∞∑n=1|an|,

Лекции:

Функциональные и степенные ряды. Радиус и интервал сходимости

Функциональный ряд — это ряд, члены которого являются функциями одной или нескольких независимых переменных, определёнными на некотором множестве, называется функциональным рядом.

Степенной ряд — это функциональный ряд вида:

в котором коэффициенты a_n берутся из некоторого кольца R.

Лекции:

Ряды Тейлора и Маклорена. Разложение элементарных функций в ряд

Ряд Тейлора — это разложение функции в бесконечную сумму степенных функций.

Ряд Маклорена — это степенной ряд, в котором слагаемыми служат действительная функция f(x) в точке 0 и её производные всех порядков в точке 0, делённые на факториал соответствующий порядку производной и умноженные на x в соответствующей степени.

Лекции:

Ряды Фурье

Ряд Фурье — это представление функции f с периодом τ в виде ряда:

Лекции:

Дифференциальные уравнения

Различные проблемы, занимавшие математиков в конце XVII и начале XVIII столетий, привели к необходимости введения такого понятия как дифференциальные уравнения. Поскольку в дифференциальных уравнениях присутствуют производные или дифференциалы функций, то первые дифференциальные уравнения появились в работах создателей интегрального и дифференциального исчисления Исаака Ньютона (1643-1727) и Готфрида Лейбница (1646-1716). Именно Ньютон в 1687 году в своих «Началах» решил дифференциальное уравнение первого порядка.

Проблемой решения дифференциальных уравнений были заняты многие математики того времени. Особо следует отметить Иоганна (1667-1748) и Якоба (1654-1705) Бернулли, предложивших решение дифференциальных уравнений первого порядка с разделяющимися переменными, однородных и линейных. Но все применявшиеся ими методы по большинству были разрозненными, единой стройной теории дифференциальных уравнений не существовало.

Методическая разработка теории дифференциальных уравнений была начата известным математиком Леонардом Эйлером (1707-1783). Вместе с ним большой вклад в развитие методов решения дифференциальных уравнений внесли французские математики Жан Даламбер (1717-1783), Жозеф Лагранж (1736-1813), Пьер Лаплас (1749-1827), немецкий математик Бернхард Риман (1826-1866). Самое главное заключается в том, что решение подобных уравнений было необходимо для практических нужд, поскольку именно присутствующая в дифференциальных уравнениях производная описывает скорость изменения различных процессов. Некоторые виды дифференциальных уравнений появились при решении задач о колеблющихся струне и колеблющейся мембране. Даламбер сформулировал правила составления дифференциальных уравнений при движении материальных систем. Дифференциальные уравнения стали основой работ Леонарда Эйлера «Физическое исследование причины морских приливов и отливов», «Исследования по вопросу о неравенствах в движении Сатурна и Юпитера», «Исследование возмущений, которые испытывает движение планет от их взаимодействия».

Нельзя не сказать о вкладе французского математика Огюстена Коши (1789-1857) в теорию дифференциальных уравнений. Он впервые поставил общую задачу о нахождении решения дифференциального уравнения с заданными начальными условиями (называемую с тех пор задачей Коши), дал способ интегрирования дифференциальных уравнений в частных производных.

Известными авторами фундаментальных трудов по дифференциальным уравнениям являются французкий математик Жак Адамар (1865-1963), российские математики Владимир Игоревич Арнольд (род. 1937 г.), Андрей Николаевич Колмогоров (1903-1987).

Кстати тут дополнительная теория из учебников по высшей математике

Дифференциальные уравнения, основные понятия

Дифференциальное уравнение — это уравнение, в которое входят производные функции и могут входить сама функция, независимая переменная и параметры. Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или могут отсутствовать вовсе, кроме хотя бы одной производной. Не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением.

Лекции:

Однородные дифференциальные уравнения первого порядка

Однородные дифференциальные уравнения первого порядка — это дифференциальное уравнение вида:

называют обыкновенным дифференциальным уравнением. Оно содержит известную функцию F, независимую переменную x, её функцию y и производные (или дифференциалы) функции y(x).

Лекции:

Линейные дифференциальные уравнения первого порядка

Линейное дифференциальное уравнения первого порядка — это дифференциальное уравнение, если в нём функция и все её производные содержатся только в первой степени, отсутствуют и их произведения.

Лекции:

Дифференциальные уравнения второго порядка

Дифференциальные уравнения второго порядка — это уравнение вида F (x; y ; y’ ; y») =0

Лекции:

Основы теории комплексных чисел

Введение комплексных чисел было связано с открытием решения кубического уравнения. В середине XVI века итальянские математики Никколо Тарталья (1499-1557) и Джероламо Кардано (1501-1576) представили миру способ решения уравнения третьей степени. Но один из возможных случаев так и остался для них загадкой. Оказалось, что при выполнении вспомогательных действий рассматриваемая система нс имела решений, а исходное уравнение имело действительный корень. На это загадочное явление впервые пролил свет другой итальянский математик Рафаэле Бомбелли (1526-1572).

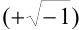
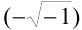
Бомбелли первым ввел в алгебру мнимые величины. Квадратный корень из отрицательного числа, как заметил Бомбелли, нс может быть ни положительным, ни отрицательным числом. Он предложил назвать эти новые «софистические» числа «плюсом из минуса» , когда их нужно складывать, и «минусом из минуса » . когда их нужно вычитать. И тогда у любого кубического уравнения прекрасно отыскивались корни! С этого момента комплексные числа уже нельзя было игнорировать. Бомбелли в своей «Алгебре» (1560, издана 1572) дал первое формальное обоснование действию над комплексными числами. Определение мнимой единицы, данное Бомбелли, за прошедшие 400 лет по свой сути нс изменилось, а арифметические действия с ней производятся именно так, как это делала Бомбелли в XVI веке.

Мнимые числа, введенные Бомбелли, более двух столетий воспринимались лишь как удобные символы. Математики применяли их только в промежуточных выкладках, но для результата использовали лишь «настоящие» — действительные числа. Лейбниц в 1702 году писал: «Мнимые числа — это прекрасное и чудесное убежище божественного духа, почти что сочетание бытия с небытием». Исчерпывающие правила действий с комплексными числами дал в середине XVIII века русский математик Леонард Эйлер (1707-1783) — один из величайших математиков всех времен и народов. Именно он предложил современное обозначение мнимой единицы — .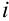

Комплексные числа не были в достаточной мере востребованы математиками еще и потому, что очень трудно было их представить. Наглядно представить мнимые числа попытался еще в XVII веке английский ученый Джон Валлис (1616-1703), но эти попытки были нс слишком удачные. В 1799 году датский математик — землемер Каспар Вессель (1745-1818) предложил простую геометрическую интерпретацию комплексных чисел, однако его работа осталась незамеченной, поскольку Вессель не имел контактов с научными кругами своего времени. Лишь через три десятка лет немецкий математик Карл Фридрих Гаусс (1777-1855) выпустил в свет свой труд «Теория биквадратных вычетов», в котором дал такое же геометрическое представление комплексных чисел, как и Вессель. Именно после опубликования этой работы в 1831 году геометрическое изображение комплексных чисел получило широкую известность и признание. Идея Веселя и Гаусса настолько прозрачна, что остается только удивляться, почему никто из ученых не додумался до нее раньше.

Алгебраическая форма комплексного числа. Геометрическая интерпретация комплексных чисел

Алгебраическая форма комплексного числа — это запись комплексного числа z в виде z=x+iy, где x и y – действительные числа, i – мнимая единица, удовлетворяющая соотношению i^<2>=-1 . Число x называется действительной частью комплексного числа z и имеет обозначение x = z. Число y называется мнимой частью комплексного числа z и имеет обозначение y = z .

Геометрическая интерпретация комплексных чисел — это kюбое комплексное число которое можно изобразить на плоскости, которую принято называть комплексной плоскостью. Комплексная плоскость аналогична прямоугольной декартовой системе координат, исключение составляют только названия осей: действительная ось (соответствует оси абсцисс); мнимая ось (соответствует оси ординат).

Лекции:

Тригонометрическая и показательная формы комплексного числа

Тригонометрическая форма комплексного числа — это запись z = r (cos φ + i sin φ) где r=√(x²+y²) — модуль комплексного числа z.

Показательная форма комплексного числа — это выражение z=re ^ i φ где r=|z|=√(x²+y²) — модуль комплексного числа, e^i φ — расширение экспоненты на случай, когда показатель степени является комплексным числом.

Лекции:

Переход между различными формами комплексных чисел

Существует три формы записи комплексных чисел: алгебраическая, тригонометрическая и показательная. Каждая форма записи удобна для решения задач, поэтому вы можете перевести комплексное число из одной формы в другую, в зависимости от поставленной задачи.

Лекции:

Численные методы

Численные методы в настоящее время относятся к основным методам решения задач математики и различных ее приложений. Они характеризуются тем, что сводят процесс решения математической задачи к некоторой конечной последовательности операций над числами и приводят к результатам, представленным в виде чисел, матриц, числовых таблиц. Их значение возрастает параллельно с развитием вычислительной техники.

Приближенные величины. Действия с приближенными числами

Все многообразие численных методов подразделяют на две группы:

• Точные – предполагают, что если вычисления ведутся точно, то с помощью конечного числа арифметических и логических операций могут быть получены точные значения искомых величин.
• Приближенные– которые даже в предположении, что вычисления ведутся без округлений, позволяют получить решение задачи лишь с заданной точностью.

Методы приближенного решения алгебраических и трансцендентных уравнений

Точные методы решения уравнений подходят только к узкому классу уравнений (квадратные, биквадратные, некоторые тригонометрические, показательные, логарифмические).

В общем случае решения уравнений находится приближённо в следующей последовательности:

• отделение (локализация) корня;
• приближённое вычисление корня до заданной точности.

Лекции:

Приближенные методы вычисления определенных интегралов

Наиболее употребляемыми приближенными методами вычисления определенных интегралов являются: метод прямоугольников, метод трапеций и метод парабол (Симпсона).

Лекции:

Численное решение обыкновенных дифференциальных уравнений методом Эйлера

Метод Эйлера — это простейший численный метод решения систем обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление». Метод Эйлера является явным, одношаговым методом первого порядка точности. Он основан на аппроксимации интегральной кривой кусочно-линейной функцией, так называемой ломаной Эйлера.

Лекции:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Системы линейных уравнений

Линейные уравнения с двумя переменными

У школьника имеется 200 рублей, чтобы пообедать в школе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе можно накупить на 200 рублей?

Обозначим количество пирожных через x , а количество чашек кофе через y . Тогда стоимость пирожных будет обозначаться через выражение 25x , а стоимость чашек кофе через 10y .

25x — стоимость x пирожных
10y — стоимость y чашек кофе

Итоговая сумма должна равняться 200 рублей. Тогда получится уравнение с двумя переменными x и y

Сколько корней имеет данное уравнение?

Всё зависит от аппетита школьника. Если он купит 6 пирожных и 5 чашек кофе, то корнями уравнения будут числа 6 и 5.

Говорят, что пара значений 6 и 5 являются корнями уравнения 25x + 10y = 200 . Записывается как (6; 5) , при этом первое число является значением переменной x , а второе — значением переменной y .

6 и 5 не единственные корни, которые обращают уравнение 25x + 10y = 200 в тождество. При желании на те же 200 рублей школьник может купить 4 пирожных и 10 чашек кофе:

В этом случае корнями уравнения 25x + 10y = 200 является пара значений (4; 10) .

Более того, школьник может вообще не покупать кофе, а купить пирожные на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 8 и 0

Или наоборот, не покупать пирожные, а купить кофе на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 0 и 20

Попробуем перечислить все возможные корни уравнения 25x + 10y = 200 . Условимся, что значения x и y принадлежат множеству целых чисел. И пусть эти значения будут бóльшими или равными нулю:

Так будет удобно и самому школьнику. Пирожные удобнее покупать целыми, чем к примеру несколько целых пирожных и половину пирожного. Кофе также удобнее брать целыми чашками, чем к примеру несколько целых чашек и половину чашки.

Заметим, что при нечетном x невозможно достичь равенства ни при каком y . Тогда значениями x будут следующие числа 0, 2, 4, 6, 8. А зная x можно без труда определить y

Таким образом, мы получили следующие пары значений (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Эти пары являются решениями или корнями уравнения 25x + 10y = 200 . Они обращают данное уравнение в тождество.

Уравнение вида ax + by = c называют линейным уравнением с двумя переменными. Решением или корнями этого уравнения называют пару значений ( x; y ), которая обращает его в тождество.

Отметим также, что если линейное уравнение с двумя переменными записано в виде ax + b y = c , то говорят, что оно записано в каноническом (нормальном) виде.

Некоторые линейные уравнения с двумя переменными могут быть приведены к каноническому виду.

Например, уравнение 2(16x + 3y − 4) = 2(12 + 8x − y) можно привести к виду ax + by = c . Раскроем скобки в обеих частях этого уравнения, получим 32x + 6y − 8 = 24 + 16x − 2y . Слагаемые, содержащие неизвестные сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой. Тогда получим 32x − 16x + 6y + 2y = 24 + 8 . Приведём подобные слагаемые в обеих частях, получим уравнение 16x + 8y = 32. Это уравнение приведено к виду ax + by = c и является каноническим.

Рассмотренное ранее уравнение 25x + 10y = 200 также является линейным уравнением с двумя переменными в каноническом виде . В этом уравнении параметры a , b и c равны значениям 25, 10 и 200 соответственно.

На самом деле уравнение ax + by = c имеет бесчисленное множество решений. Решая уравнение 25x + 10y = 200, мы искали его корни только на множестве целых чисел. В результате получили несколько пар значений, которые обращали данное уравнение в тождество. Но на множестве рациональных чисел уравнение 25x + 10y = 200 будет иметь бесчисленное множество решений.

Для получения новых пар значений, нужно взять произвольное значение для x , затем выразить y . К примеру, возьмем для переменной x значение 7. Тогда получим уравнение с одной переменной 25 × 7 + 10y = 200 в котором можно выразить y

Пусть x = 15 . Тогда уравнение 25x + 10y = 200 примет вид 25 × 15 + 10y = 200. Отсюда находим, что y = −17,5

Пусть x = −3 . Тогда уравнение 25x + 10y = 200 примет вид 25 × (−3) + 10y = 200. Отсюда находим, что y = 27,5

Система двух линейных уравнений с двумя переменными

Для уравнения ax + by = c можно сколько угодно раз брать произвольные значение для x и находить значения для y . Отдельно взятое такое уравнение будет иметь бесчисленное множество решений.

Но бывает и так, что переменные x и y связаны не одним, а двумя уравнениями. В этом случае они образуют так называемую систему линейных уравнений с двумя переменными. Такая система уравнений может иметь одну пару значений (или по-другому: «одно решение»).

Может случиться и так, что система вовсе не имеет решений. Бесчисленное множество решений система линейных уравнений может иметь в редких и в исключительных случаях.

Два линейных уравнения образуют систему тогда, когда значения x и y входят в каждое из этих уравнений.

Вернемся к самому первому уравнению 25x + 10y = 200 . Одной из пар значений для этого уравнения была пара (6; 5) . Это случай, когда на 200 рублей можно можно было купить 6 пирожных и 5 чашек кофе.

Составим задачу так, чтобы пара (6; 5) стала единственным решением для уравнения 25x + 10y = 200 . Для этого составим ещё одно уравнение, которое связывало бы те же x пирожных и y чашечек кофе.

Поставим текст задачи следующим образом:

«Школьник купил на 200 рублей несколько пирожных и несколько чашек кофе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе купил школьник, если известно что количество пирожных на одну единицу больше количества чашек кофе?»

Первое уравнение у нас уже есть. Это уравнение 25x + 10y = 200 . Теперь составим уравнение к условию «количество пирожных на одну единицу больше количества чашек кофе» .

Количество пирожных это x , а количество чашек кофе это y . Можно записать эту фразу с помощью уравнения x − y = 1. Это уравнение будет означать, что разница между пирожными и кофе составляет 1.

Либо второе уравнение можно записать как x = y + 1 . Это уравнение означает, что количество пирожных на единицу больше, чем количество чашек кофе. Поэтому для получения равенства, к количеству чашек кофе прибавлена единица. Это легко можно понять, если воспользоваться моделью весов, которые мы рассматривали при изучении простейших задач:

Получили два уравнения: 25x + 10y = 200 и x = y + 1. Поскольку значения x и y , а именно 6 и 5 входят в каждое из этих уравнений , то вместе они образуют систему. Запишем эту систему. Если уравнения образуют систему, то они обрамляются знаком системы. Знак системы это фигурная скобка:

Давайте решим данную систему. Это позволит увидеть, как мы придём к значениям 6 и 5. Существует много методов решения таких систем. Рассмотрим наиболее популярные из них.

Метод подстановки

Название этого метода говорит само за себя. Суть его заключается в том, чтобы одно уравнение подставить в другое, предварительно выразив одну из переменных.

В нашей системе ничего выражать не нужно. Во втором уравнении x = y + 1 переменная x уже выражена. Эта переменная равна выражению y + 1 . Тогда можно подставить это выражение в первое уравнение вместо переменной x

После подстановки выражения y + 1 в первое уравнение вместо x , получим уравнение 25(y + 1) + 10y = 200 . Это линейное уравнение с одной переменной. Такое уравнение решить довольно просто:

Мы нашли значение переменной y . Теперь подставим это значение в одно из уравнений и найдём значение x . Для этого удобно использовать второе уравнение x = y + 1 . В него и подставим значение y

Значит пара (6; 5) является решением системы уравнений, как мы и задумывали. Выполняем проверку и убеждаемся, что пара (6; 5) удовлетворяет системе:

Пример 2. Решить методом подстановки следующую систему уравнений:

Подставим первое уравнение x = 2 + y во второе уравнение 3x − 2y = 9 . В первом уравнении переменная x равна выражению 2 + y . Это выражение и подставим во второе уравнение вместо x

Теперь найдём значение x . Для этого подставим значение y в первое уравнение x = 2 + y

Значит решением системы 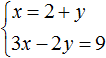является пара значение (5; 3)

Пример 3. Решить методом подстановки следующую систему уравнений:

Здесь в отличие от предыдущих примеров, одна из переменных не выражена явно.

Чтобы подставить одно уравнение в другое, сначала нужно выразить одну из переменных.

Выражать желательно ту переменную, которая имеет коэффициент единицу. Коэффициент единицу имеет переменная x , которая содержится в первом уравнении x + 2y = 11 . Эту переменную и выразим.

После выражения переменной x , наша система примет следующий вид:

Теперь подставим первое уравнение во второе и найдем значение y

Подставим y в первое уравнение и найдём x

Значит решением системы 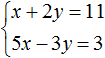является пара значений (3; 4)

Конечно, выражать можно и переменную y . Корни от этого не изменятся. Но если выразить y, получится не очень-то и простое уравнение, на решение которого уйдет больше времени. Выглядеть это будет следующим образом:

Видим, что в данном примере выражать x намного удобнее, чем выражать y .

Пример 4. Решить методом подстановки следующую систему уравнений:

Выразим в первом уравнении x . Тогда система примет вид:

Подставим первое уравнение во второе и найдём y

Подставим y в первое уравнение и найдём x . Можно воспользоваться изначальным уравнением 7x + 9y = 8 , либо воспользоваться уравнением 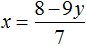, в котором выражена переменная x . Этим уравнением и воспользуемся, поскольку это удобно:

Значит решением системы 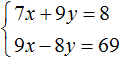является пара значений (5; −3)

Метод сложения

Метод сложения заключается в том, чтобы почленно сложить уравнения, входящие в систему. Это сложение приводит к тому, что образуется новое уравнение с одной переменной. А решить такое уравнение довольно просто.

Решим следующую систему уравнений:

Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. Получим следующее равенство:

Приведем подобные слагаемые:

В результате получили простейшее уравнение 3x = 27 корень которого равен 9. Зная значение x можно найти значение y . Подставим значение x во второе уравнение x − y = 3 . Получим 9 − y = 3 . Отсюда y = 6 .

Значит решением системы 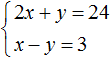является пара значений (9; 6)

Пример 2. Решить следующую систему уравнений методом сложения:

Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. В получившемся равенстве приведем подобные слагаемые:

В результате получили простейшее уравнение 5 x = 20, корень которого равен 4. Зная значение x можно найти значение y . Подставим значение x в первое уравнение 2 x + y = 11 . Получим 8 + y = 11 . Отсюда y = 3 .

Значит решением системы 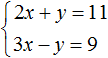является пара значений (4;3)

Процесс сложения подробно не расписывают. Его нужно выполнять в уме. При сложении оба уравнения должны быть приведены к каноническому виду. То есть к виду ax + by = c .

Из рассмотренных примеров видно, что основная цель сложения уравнений это избавление от одной из переменных. Но не всегда удаётся сразу решить систему уравнений методом сложения. Чаще всего систему предварительно приводят к виду, при котором можно сложить уравнения, входящие в эту систему.

Например, систему 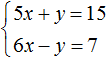можно сразу решить методом сложения. При сложении обоих уравнений, слагаемые y и −y исчезнут, поскольку их сумма равна нулю. В результате образуется простейшее уравнение 11x = 22 , корень которого равен 2. Затем можно будет определить y равный 5.

А систему уравнений 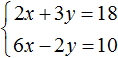методом сложения сразу решить нельзя, поскольку это не приведёт к исчезновению одной из переменных. Сложение приведет к тому, что образуется уравнение 8x + y = 28 , имеющее бесчисленное множество решений.

Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному. Это правило справедливо и для системы линейных уравнений с двумя переменными. Одно из уравнений (или оба уравнения) можно умножить на какое-нибудь число. В результате получится равносильная система, корни которой будут совпадать с предыдущей.

Вернемся к самой первой системе 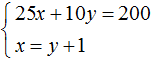, которая описывала сколько пирожных и чашек кофе купил школьник. Решением этой системы являлась пара значений (6; 5) .

Умножим оба уравнения, входящие в эту систему на какие-нибудь числа. Скажем первое уравнение умножим на 2, а второе на 3

В результате получили систему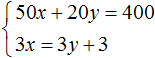
Решением этой системы по-прежнему является пара значений (6; 5)

Это значит, что уравнения входящие в систему можно привести к виду, пригодному для применения метода сложения.

Вернемся к системе 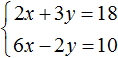, которую мы не смогли решить методом сложения.

Умножим первое уравнение на 6, а второе на −2

Тогда получим следующую систему:

Сложим уравнения, входящие в эту систему. Сложение компонентов 12x и −12x даст в результате 0, сложение 18y и 4y даст 22y , а сложение 108 и −20 даст 88. Тогда получится уравнение 22y = 88 , отсюда y = 4 .

Если первое время тяжело складывать уравнения в уме, то можно записывать как складывается левая часть первого уравнения с левой частью второго уравнения, а правая часть первого уравнения с правой частью второго уравнения:

Зная, что значение переменной y равно 4, можно найти значение x. Подставим y в одно из уравнений, например в первое уравнение 2x + 3y = 18 . Тогда получим уравнение с одной переменной 2x + 12 = 18 . Перенесем 12 в правую часть, изменив знак, получим 2x = 6 , отсюда x = 3 .

Пример 4. Решить следующую систему уравнений методом сложения:

Умножим второе уравнение на −1. Тогда система примет следующий вид:

Сложим оба уравнения. Сложение компонентов x и −x даст в результате 0, сложение 5y и 3y даст 8y , а сложение 7 и 1 даст 8. В результате получится уравнение 8y = 8 , корень которого равен 1. Зная, что значение y равно 1, можно найти значение x .

Подставим y в первое уравнение, получим x + 5 = 7 , отсюда x = 2

Пример 5. Решить следующую систему уравнений методом сложения:

Желательно, чтобы слагаемые содержащие одинаковые переменные, располагались друг под другом. Поэтому во втором уравнении слагаемые 5y и −2x поменяем местами. В результате система примет вид:

Умножим второе уравнение на 3. Тогда система примет вид:

Теперь сложим оба уравнения. В результате сложения получим уравнение 8y = 16 , корень которого равен 2.

Подставим y в первое уравнение, получим 6x − 14 = 40 . Перенесем слагаемое −14 в правую часть, изменив знак, получим 6x = 54 . Отсюда x = 9.

Пример 6. Решить следующую систему уравнений методом сложения:

Избавимся от дробей. Умножим первое уравнение на 36, а второе на 12

В получившейся системе 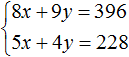первое уравнение можно умножить на −5, а второе на 8

Сложим уравнения в получившейся системе. Тогда получим простейшее уравнение −13y = −156 . Отсюда y = 12 . Подставим y в первое уравнение и найдем x

Пример 7. Решить следующую систему уравнений методом сложения:

Приведем оба уравнения к нормальному виду. Здесь удобно применить правило пропорции в обоих уравнениях. Если в первом уравнении правую часть представить как , а правую часть второго уравнения как , то система примет вид:

У нас получилась пропорция. Перемножим её крайние и средние члены. Тогда система примет вид:

Первое уравнение умножим на −3, а во втором раскроем скобки:

Теперь сложим оба уравнения. В результате сложения этих уравнений, мы получим равенство, в обеих частях которого будет ноль:

Получается, что система 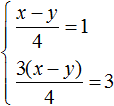имеет бесчисленное множество решений.

Но мы не можем просто так взять с неба произвольные значения для x и y . Мы можем указать одно из значений, а другое определится в зависимости от значения, указанного нами. Например, пусть x = 2 . Подставим это значение в систему:

В результате решения одного из уравнений, определится значение для y , которое будет удовлетворять обоим уравнениям:

Получившаяся пара значений (2; −2) будет удовлетворять системе:

Найдём еще одну пару значений. Пусть x = 4. Подставим это значение в систему:

На глаз можно определить, что значение y равно нулю. Тогда получим пару значений (4; 0), которая удовлетворяет нашей системе:

Пример 8. Решить следующую систему уравнений методом сложения:

Умножим первое уравнение на 6, а второе на 12

Перепишем то, что осталось:

Раскроем скобки в обоих уравнениях и приведём подобные слагаемые:

Первое уравнение умножим на −1. Тогда система примет вид:

Теперь сложим оба уравнения. В результате сложения образуется уравнение 6b = 48 , корень которого равен 8. Подставим b в первое уравнение и найдём a

Система линейных уравнений с тремя переменными

В линейное уравнение с тремя переменными входит три переменные с коэффициентами, а также свободный член. В каноническом виде его можно записать следующим образом:

Данное уравнение имеет бесчисленное множество решений. Придавая двум переменным различные значения, можно найти третье значение. Решением в этом случае является тройка значений (x; y; z) которая обращает уравнение в тождество.

Если переменные x, y, z связаны между собой тремя уравнениями, то образуется система трех линейных уравнений с тремя переменными. Для решения такой системы можно применять те же методы, которые применяются к линейным уравнениям с двумя переменными: метод подстановки и метод сложения.

Пример 1. Решить следующую систему уравнений методом подстановки:

Выразим в третьем уравнении x . Тогда система примет вид:

Теперь выполним подстановку. Переменная x равна выражению 3 − 2y − 2z . Подставим это выражение в первое и второе уравнение:

Раскроем скобки в обоих уравнениях и приведём подобные слагаемые:

Мы пришли к системе линейных уравнений с двумя переменными. В данном случае удобно применить метод сложения. В результате переменная y исчезнет, и мы сможем найти значение переменной z

Теперь найдём значение y . Для этого удобно воспользоваться уравнением −y + z = 4. Подставим в него значение z

Теперь найдём значение x . Для этого удобно воспользоваться уравнением x = 3 − 2y − 2z . Подставим в него значения y и z

Таким образом, тройка значений (3; −2; 2) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:

Пример 2. Решить систему методом сложения

Сложим первое уравнение со вторым, умноженным на −2.

Если второе уравнение умножить на −2, то оно примет вид −6x + 6y − 4z = −4 . Теперь сложим его с первым уравнением:

Видим, что в результате элементарных преобразований, определилось значение переменной x . Оно равно единице.

Вернемся к главной системе. Сложим второе уравнение с третьим, умноженным на −1. Если третье уравнение умножить на −1, то оно примет вид −4x + 5y − 2z = −1 . Теперь сложим его со вторым уравнением:

Получили уравнение x − 2y = −1 . Подставим в него значение x , которое мы находили ранее. Тогда мы сможем определить значение y

Теперь нам известны значения x и y . Это позволяет определить значение z . Воспользуемся одним из уравнений, входящим в систему:

Таким образом, тройка значений (1; 1; 1) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:

Задачи на составление систем линейных уравнений

Задача на составление систем уравнений решается путем ввода нескольких переменных. Далее составляются уравнения на основании условий задачи. Из составленных уравнений образуют систему и решают её. Решив систему, необходимо выполнить проверку на то, удовлетворяет ли её решение условиям задачи.

Задача 1. Из города в колхоз выехала машина «Волга». Обратно она возвращалась по другой дороге, которая была на 5 км короче первой. Всего в оба конца машина проехала 35 км. Сколько километров составляет длина каждой дороги?

Решение

Пусть x — длина первой дороги, y — длина второй. Если в оба конца машина проехала 35 км, то первое уравнение можно записать как x + y = 35. Это уравнение описывает сумму длин обеих дорог.

Сказано, что обратно машина возвращалась по дороге которая была короче первой на 5 км. Тогда второе уравнение можно записать как x − y = 5. Это уравнение показывает, что разница между длинами дорог составляет 5 км.

Либо второе уравнение можно записать как x = y + 5 . Этим уравнением и воспользуемся.

Поскольку переменные x и y в обоих уравнениях обозначают одно и то же число, то мы можем образовать из них систему:

Решим эту систему каким-нибудь из изученных ранее методов. В данном случае удобно воспользоваться методом подстановки, поскольку во втором уравнении переменная x уже выражена.

Подставим второе уравнение в первое и найдём y

Подставим найденное значение y в во второе уравнение x = y + 5 и найдём x

Длина первой дороги была обозначена через переменную x . Теперь мы нашли её значение. Переменная x равна 20. Значит длина первой дороги составляет 20 км.

А длина второй дороги была обозначена через y . Значение этой переменной равно 15. Значит длина второй дороги составляет 15 км.

Выполним проверку. Для начала убедимся, что система решена правильно:

Теперь проверим удовлетворяет ли решение (20; 15) условиям задачи.

Было сказано, что всего в оба конца машина проехала 35 км. Складываем длины обеих дорог и убеждаемся, что решение (20; 15) удовлетворяет данному условию: 20 км + 15 км = 35 км

Следующее условие: обратно машина возвращалась по другой дороге, которая была на 5 км короче первой . Видим, что решение (20; 15) удовлетворяет и этому условию, поскольку 15 км короче, чем 20 км на 5 км: 20 км − 15 км = 5 км

При составлении системы важно, чтобы переменные обозначали одни и те же числа во всех уравнениях, входящих в эту систему.

Так наша система 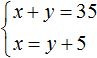содержит два уравнения. Эти уравнения в свою очередь содержат переменные x и y , которые обозначают одни и те же числа в обоих уравнениях, а именно длины дорог, равных 20 км и 15 км.

Задача 2. На платформу были погружены дубовые и сосновые шпалы, всего 300 шпал. Известно, что все дубовые шпалы весили на 1 т меньше, чем все сосновые. Определить, сколько было дубовых и сосновых шпал отдельно, если каждая дубовая шпала весила 46 кг, а каждая сосновая 28 кг.

Решение

Пусть x дубовых и y сосновых шпал было погружено на платформу. Если всего шпал было 300, то первое уравнение можно записать как x + y = 300 .

Все дубовые шпалы весили 46x кг, а сосновые весили 28y кг. Поскольку дубовые шпалы весили на 1 т меньше, чем сосновые, то второе уравнение можно записать, как 28y − 46x = 1000 . Это уравнение показывает, что разница масс между дубовыми и сосновыми шпалами, составляет 1000 кг.

В результате получаем два уравнения, которые образуют систему

Решим данную систему. Выразим в первом уравнении x . Тогда система примет вид:

Подставим первое уравнение во второе и найдём y

Подставим y в уравнение x = 300 − y и узнаем чему равно x

Значит на платформу было погружено 100 дубовых и 200 сосновых шпал.

Проверим удовлетворяет ли решение (100; 200) условиям задачи. Для начала убедимся, что система решена правильно:

Было сказано, что всего было 300 шпал. Складываем количество дубовых и сосновых шпал и убеждаемся, что решение (100; 200) удовлетворяет данному условию: 100 + 200 = 300.

Следующее условие: все дубовые шпалы весили на 1 т меньше, чем все сосновые . Видим, что решение (100; 200) удовлетворяет и этому условию, поскольку 46 × 100 кг дубовых шпал легче, чем 28 × 200 кг сосновых шпал: 5600 кг − 4600 кг = 1000 кг.

Задача 3. Взяли три куска сплава меди с никелем в отношениях 2 : 1 , 3 : 1 и 5 : 1 по массе. Из них сплавлен кусок массой 12 кг с отношением содержания меди и никеля 4 : 1 . Найдите массу каждого исходного куска, если масса первого из них вдвое больше массы второго.

Решение

Пусть x — масса первого куска, y — масса второго куска, z — масса третьего куска. Если из этих кусков сплавлен кусок массой 12 кг, то первое уравнение можно записать как x + y + z = 12 .

Масса первого куска вдвое больше массы второго куска. Тогда второе уравнение можно записать как x = 2y .

Полученных двух уравнений недостаточно для решения данной задачи. Если второе уравнение подставить в первое, то мы получим уравнение 2y + y + z = 12 , откуда 3y + z = 12 . Это уравнение имеет бесчисленное множество решений.

Составим ещё одно уравнение. Пусть это уравнение будет описывать количество меди, взятого с каждого сплава и сколько меди оказалось в получившемся сплаве.

Если первый сплав имеет массу x , а медь и никель находится нём в отношении 2 : 1 , то можно записать, что в новом сплаве содержится 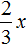меди от первого куска.

Если второй сплав имеет массу y , а медь и никель находится в нём в отношении 3 : 1 , то можно записать, что в новом сплаве содержится 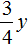меди от второго куска.

Если третий сплав имеет массу z , а медь и никель находится в отношении 5 : 1 , то можно записать, что в новом сплаве содержится 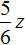меди от третьего куска.

Полученный сплав имеет имеет массу 12 кг, а медь и никель находится в нём в отношении 4 : 1 . Тогда можно записать, что в полученном сплаве содержится 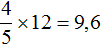меди.

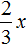
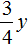
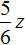
Сложим , , и приравняем эту сумму к 9,6. Это и будет нашим третьим уравнением:

Попробуем решить данную систему.

Для начала упростим третье уравнение. Подставим в него второе уравнение и посмотрим, что из этого выйдет:

Теперь в главной системе вместо уравнения 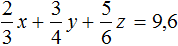запишем уравнение, которое мы сейчас получили, а именно уравнение 25y + 10z = 115,2

Подставим второе уравнение в первое:

Умножим первое уравнение на −10 . Тогда система примет вид:

Сложим оба уравнения. Тогда получим простейшее уравнение −5y = −4,8 откуда найдём y равный 0,96 . Значит масса второго сплава составляет 0,96 кг .

Теперь найдём x . Для этого удобно воспользоваться уравнением x = 2y. Значение y уже известно. Осталось только подставить его:

Значит масса первого сплава составляет 1,92 кг .

Теперь найдём z . Для этого удобно воспользоваться уравнением x + y + z = 12 . Значения x и y уже известны. Подставим их куда нужно:

Значит масса третьего сплава составляет 9,12 кг.