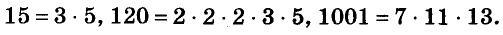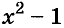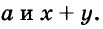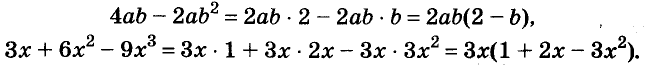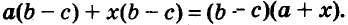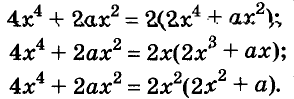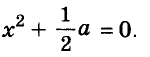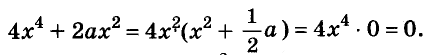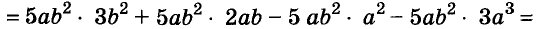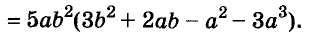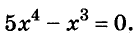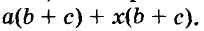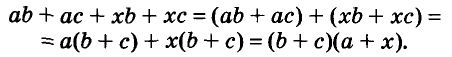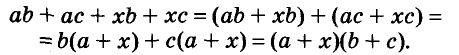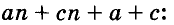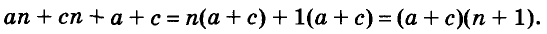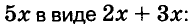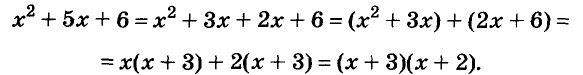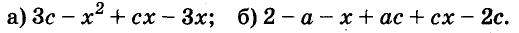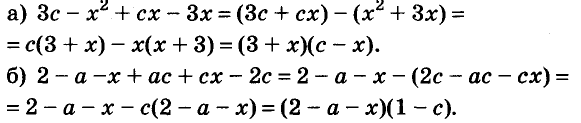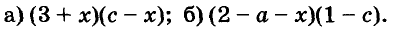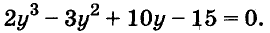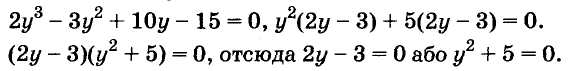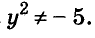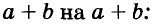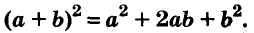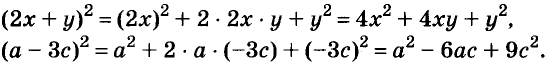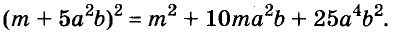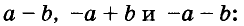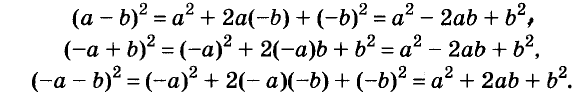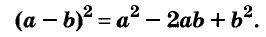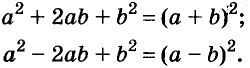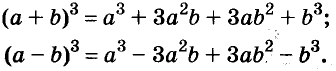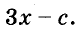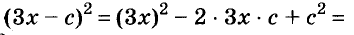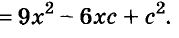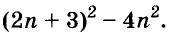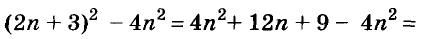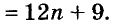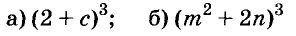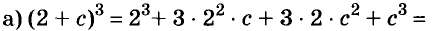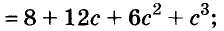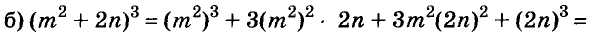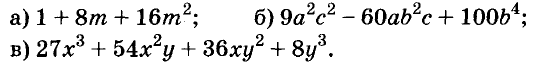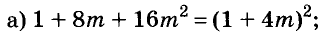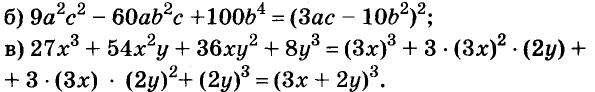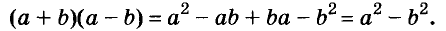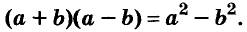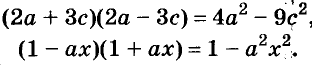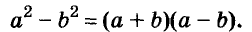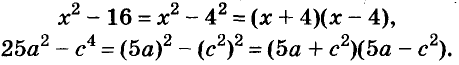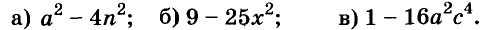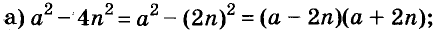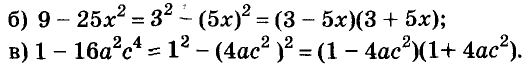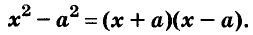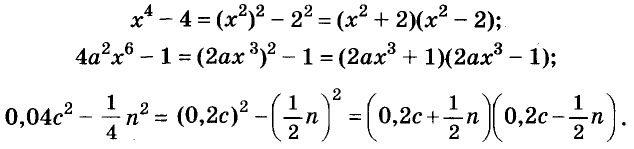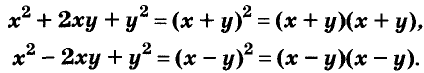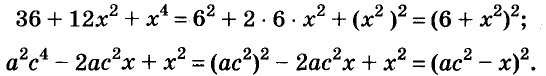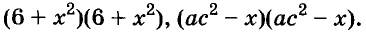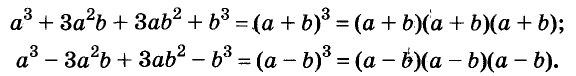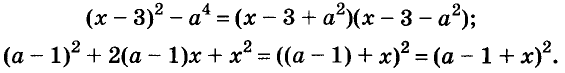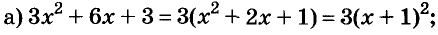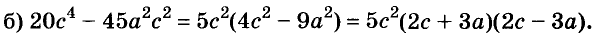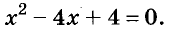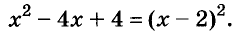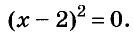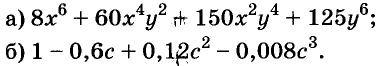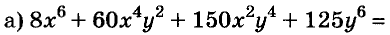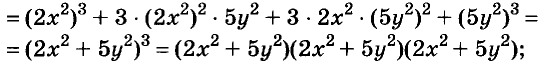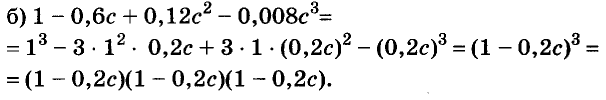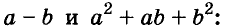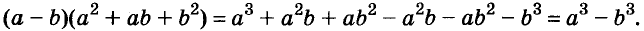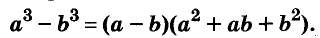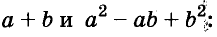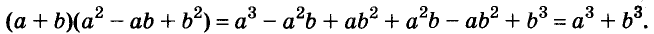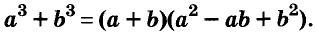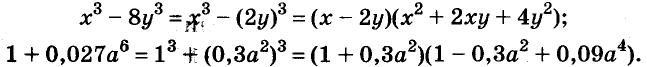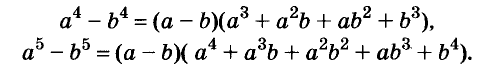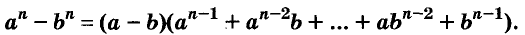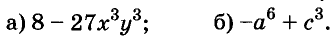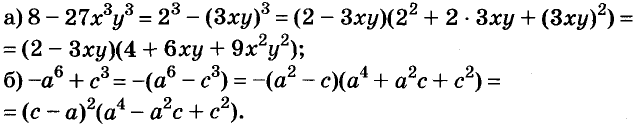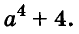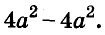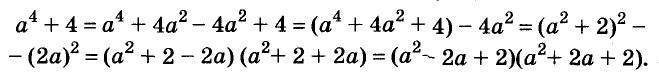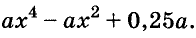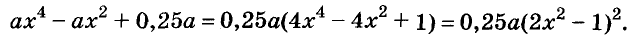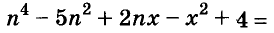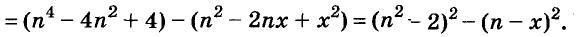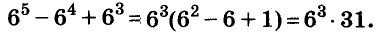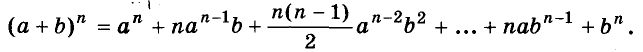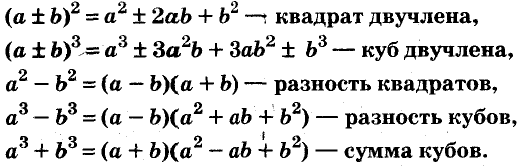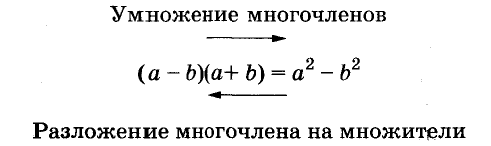Разложение разности квадратов на множители уравнение

Разложение разности квадратов на множители

Разделы: Математика

Цель урока: расширить знания учащихся о способах разложения многочлена на множители.

Задачи урока:
1. создать условия для актуализации ранее полученных знаний о разложении многочленов на множители;
2. способствовать приобретению навыков разложения многочленов на множители с помощью формулы a 2 – b 2 = (a – b)(a + b)
3. способствовать развитию познавательного интереса учащихся.
4. развивать умение анализировать, обобщать, делать выводы, развивать математическую речь учащихся (устную и письменную); формировать навыки самостоятельной работы с учебником, навыки самоконтроля, взаимоконтроля.

Тип урока: урок формирования умений и навыков.

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала(самостоятельная работа).

1) Вычислите произведение чисел:

2) Выполните умножение:

а) (3a – 4b)(3a + 4b);
б) (-6a – 5b)(6a –5b).

3) Упростите выражение: (2a – 3b)(2a + 3b) + 9b(b + 1).

1) Вычислите произведение чисел:

2) Выполните умножение:

а) (2b – 3a)(2b + 3a);
б) (-4a – 5b)(4a – 5b)

3) Упростите выражение: (3a – 4b)(3a + 4b) – 9b(a – 1).

III. Изучение нового материала.

В равенстве (a –b)(a + b) = a 2 – b 2 поменяем местами части и получим тождество a 2 – b 2 = (a – b)(a + b). Разность квадратов двух чисел (выражений) равна произведению разности этих чисел (выражений) и их суммы. Такое тождество называют формулой разности квадратов. Её используют для разложения на множители разности квадратов чисел или выражений.

Докажем, что число 47 4 – 32 2 составное .

Используем формулу разности квадратов и получим:

47 4 – 32 2 = (47 2 ) – 32 2 = (47 2 – 32)(47 2 + 32).

Видно, что у данного числа есть множители 47 2 – 32 и 47 2 + 32.Поэтому такое число по определению является составным.

Докажем, что число 16 4 – 231 2 кратно 25.

Применим формулу разности квадратов и получим: 16 4 – 231 2 = (16 2 ) 2 – 231 2 = 256 2 – 231 2 = (256 – 231)(256 + 231) = 25*487.

Так как данное число имеет делитель 25, то оно кратно 25.

Сократим дробь

Используя формулу разности квадратов, разложим числитель и знаменатель дроби на множители. Имеем:

Найдём значение выражения 100 2 – 99 2 + 98 2 – 97 2 +…+ 2 2 – 1 2 .

В приведённую сумму входят 100 чисел. Сгруппируем их последовательно попарно и используем формулу разности квадратов. Получаем:

100 2 – 99 2 + 98 2 – 97 2 +…+ 2 2 – 1 2 = (100 2 – 99 2 ) + (98 2 – 97 2 ) +…+ (2 2 – 1 2 ) = (100 – 99)(100 + 99) + (98 – 97)(98 + 97) +…+ (2 – 1)(2 + 1)= 1*199 + 1*195 +…+ 1*7 + 1*3 = 199 + 195 +…+ 7 + 3.

После группировки членов получилось 50 выражений, поэтому надо сложить 50 чисел. Каждое следующее число на 4 меньше предыдущего (т.е. числа образуют арифметическую прогрессию).

Чтобы найти сумму чисел так же сгруппируем их попарно: первое с последним, второе с предпоследним и т.д. Имеем: 199 + 195 +…+ 7 + 3=(199 + 3) + (195 + 7) +… = 202 +…+ 202*25 =5050.

Заметим, что при попарной группировке 50 чисел получилось 25 скобок и затем 25 одинаковых чисел 202.

Разложим на множители выражение 25х 4 – 16у 2 .

Представим этот двучлен в виде разности квадратов и используем формулу разности квадратов:

25х 4 – 16у 2 = (5х 2 ) 2 – (4у) 2 = (5х 2 – 4у)(5х 2 + 4у).

Разложим на множители квадратный трёхчлен х 2 + 4х + 3.

Дополним это выражение до квадрата суммы:

Х 2 + 4х + 3 = х 2 + 4х + 4 –1 = (х 2 + 4х + 4) – 1 = (х + 2) 2 – 1 2

Затем применим формулу разности квадратов:

(х + 2) 2 – 1 = (х + 2 – 1)(х + 2 + 1) = (х + 1)(х + 3).

Таким образом, получили х 2 + 4х + 3 = (х + 1)(х + 3)

Заметим, что ранее для разложения квадратных трёхчленов использовали способ группировки членов. Представим член 4х в виде 4х = х + 3х.

Тогда имеем: х 2 + 4х + 3 = х 2 + х + 3х + 3 = (х 2 + х) + (3х + 3) = х(х + 1) + 3(х + 1) = (х + 1)(х + 3).

Разложим на множители двучлен n 4 + 4.

Для разложения двучлена дополним его до квадрата суммы .Для этого прибавим и вычтем 4n 2 и используем формулу разности квадратов. Получаем: n 4 + 4 = n 4 + 4 + 4n 2 – 4n 2 = (n 4 + 4n 2 + 4) – 4n 2 = (n 3 + 2) 2 – (2n) 2 = (n 2 + 2 – 2n)(n 2 + 2 – 2n) = (n 2 – 2n + 2)(n 2 + 2n + 2).

IV. Задание на уроке.

№ 939(в); 940(б); 942(б, г); 943(а); 944(д); 945(в); 946(б, д); 948(в); 951(а, д); 953(а).

V. Задание на дом.

VI. Творческие задания.

1. Разложите на множители выражение:

а) х 2 + 6х+ 8;
б) 8 – х –х 2 ;
в) х 2 + 14х + 48;
г) -х 2 + 10х –24;
д) 4х 2 + 1;
е) х 4 + х 2 + 1.

(Ответы: а) (х + 2)(х + 4); б) (х + 4)(2 – х); в) (х + 6)(х + 8); г) (х –4)(6 – х); д) (2х 2 – 2х + 1)(2х 2 + 2х + 1) (добавить и вычесть 4х 2 ); е) (х 2 – х +1)(х 2 + х + 1) (добавить и вычесть х 2 ).)

2. Докажите,что при любом натуральном n значение выражения:

а) (3n 2 + 2) 2 – 4 2 кратно 3;
б) (5n + 1) 2 – 9 2 кратно 5;
в) (4n + 1) 2 – (2n + 5) 2 кратно 6;
г) (3n + 4) 2 – (4n + 3) 2 кратно 7.

Формулы сокращенного умножения. Разложение на множители.

теория по математике 📈 алгебраические выражения

Очень часто нам встречаются выражения, которые требуют различных преобразований. Для того, чтобы это короче выполнять в некоторых случаях, существуют специальные формулы сокращенного умножения.

Квадрат суммы и квадрат разности

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения:

(a+b) 2 =a 2 +2ab+b 2

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения:

(a–b) 2 =a 2 –2ab+b 2

Если сравнить два этих правила и формулы, то видно, что при возведении в квадрат есть отличие в знаках только перед удвоенным произведением. Рассмотрим применение данных формул на примерах.

Пример №1. Преобразуем выражение в многочлен: (с+8) 2 . По правилу выполняем последовательно: квадрат первого выражения это с 2 ; удвоенное произведение первого и второго выражения – это 2с8; квадрат второго выражения – это 8 2 . Выполним запись: (с+8) 2 =с 2 +2с8+8 2 . Теперь выполним умножение и возведение в степень чисел: (с+8) 2 =с 2 +2с8+8 2 =с 2 +16с+64. Получим многочлен. Промежуточные действия, выделенные жирным шрифтом, можно не записывать, а выполнять их устно.

Пример №2. Представим в виде многочлена выражение (2х–11) 2 . Выполним возведение в квадрат по правилу квадрата разности двух выражений: (2х–11) 2 =(2х) 2 –2•2х•11+11 2 =4х 2 –44х+121.

Пример №3. Представим в виде многочлена квадрат двучлена (–9х+4у) 2 . В данном выражении на первом месте стоит отрицательное число, на втором положительное, что не привычно для нас по работе с формулой. Но мы знаем, что можно просто поменять слагаемые местами, тогда получится разность двух выражений, которую возводим в квадрат по соответствующей формуле: (–9х+4у) 2 =(4у–9х) 2 =16у 2 –72ху+81х 2 .

Пример №4. Представим в виде многочлена выражение (–6с–10) 2 . Данное выражение содержит два слагаемых с минусом. Надо просто запомнить, что оно будет равносильно выражению (6с+10) 2 , потому что квадраты противоположных чисел равны (а 2 =(–а) 2 ) . Возведем данное выражение в квадрат по формуле квадрата суммы двух выражений: (–6с–10) 2 =(6с+10) 2 =36с 2 +120с+100.

Куб суммы и разности

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго плюс куб второго выражения:

(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго минус куб второго выражения:

(a–b) 3 =a 3 –3a 2 b+3ab 2 –b 3

Используя данные формулы, можно возводить в куб сумму и разность двух выражений. В данном случае не нужно выполнять промежуточные действия устно, чтобы избежать ошибок.

Пример №5. Возведем в куб сумму с+5а. Всё выполним и распишем строго по формуле:

(с+5а) 3 =с 3 +3с 2 •5а+3с(5а) 2 +(5а) 3 =с 3 +15ас 2 +75а 2 с+125а 3 .

Пример №6. Возведем в куб разность:

(х–10) 3 =х 3 –3х 2 10+3х10 2 –10 3 =х 3 –30х 2 +300х–1000.

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:

a 2 –b 2 =(a–b)(a+b)

Пример №7. Выполним умножение: (4–с)(4+с)=4 2 –с 2 =16–с 2 в данном выражении выполнили всё в соответствии с формулой: возвели в квадрат 4 и число с. Промежуточные записи (выделены жирным шрифтом) можно не делать, а выполнять их устно.

Пример №8. Упростим выражение: (5с+а)(5с–а)=25с 2 –а 2 в данном выражении мы видим, что первый множитель сумма, а второй – разность. Для выполнения задания по данной формуле это не имеет значения, так как мы знаем, что от перестановки множителей произведение не изменяется.

Применение формул сокращенного умножения для разложения многочленов на множители

Рассмотрим тождество, которое называют разностью квадратов двух выражений:

a 2 –b 2 =(a–b)(a+b)

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы. Эту формулу применяют для разложения на множители многочлена, содержащего разность квадратов. Рассмотрим на примерах.

Пример №9. Разложить на множители многочлен 100–с 2 . Из условия видно, что число 100 – это квадрат числа 10, следовательно, 100–с 2 =10 2 –с 2 , значит можно разложить на множители по формуле: 100–с 2 =10 2 –с 2 =(10–с)(10+с). Выделенное жирным шрифтом выражение можно не записывать, а выполнять устно.

Пример №10. Разложить на множители: х 2 у 2 –81=(ху–9)(ху+9). В данном выражении выполнено всё в соответствии с формулой, промежуточные записи не использованы.

Пример №11. Представим в виде произведения: х 4 –36=(х 2 –6)(х 2 +6). В данном выражении мы видим, что степень переменной может быть не только вторая, но и любая четная, чтобы ее можно было представить в виде квадрата переменной.

Пример №12. Представим в виде произведения х 10 с 6 –25=(х 5 с 3 –5)(х 5 с 3 +5). Здесь показаны разные четные степени переменных.

Для разложения на множители суммы и разности кубов существуют определенные правила и формулы.

Сумма и разность кубов

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности:

a 3 +b 3 =(a+b)(a 2 –ab+b 2 )

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:

a 3 –b 3 =(a–b)(a 2 +ab+b 2 )

Пример №13. Разложим на множители многочлен 8+с 3 . В данном случае мы видим число 8, которое нужно представить в виде куба числа, это будет 2 3 . Значит, 8+с 3 =2 3 +с 3 . Далее распишем по формуле суммы кубов: 8+с 3 =2 3 +с 3 =(2+с)(4–2с+с 2 ).

Пример №14. Запишем в виде произведения разность х 3 –а 12 . В этом выражении есть степень, отличная от третьей, поэтому представим а 12 в виде куба числа (а 4 ) 3 . Получим: х 3 –а 12 =х 3 –(а 4 ) 3 . Разложим на множители по формуле разности кубов: х 3 –а 12 =х 3 –(а 4 ) 3 =(х–а 4 )(х 2 +ха 4 +а 8 ).

Разложение многочлена формулой квадрата суммы и разности

Формулы квадрата суммы и квадрата разности также используют для разложения многочлена на множители. Для этого формулы записываются в обратном порядке, то есть меняются левая и правая части местами:

a 2 +2ab+b 2 =(a+b) 2

a 2 –2ab+b 2 =(a–b) 2

Пример №15. Преобразовать трехчлен 4х 2 +12х+9 в квадрат двучлена. Для этого определим, где здесь числа, которые можно представить в виде квадрата, это будут 4х 2 и 9, так как 4х 2 =(2х) 2 , а 9=3 2 . Соответственно проверим, является ли 12х удвоенным произведением чисел 2х и 3: 22х3=12х. Выполняем запись: 4х 2 +12х+9=(2х) 2 +2•2х•3+3 2 =(2х+3) 2 . Обычно промежуточное действие (выделено жирным) не записывается, квадраты чисел определяются устно.

Пример №16. Разложить на множители многочлен –16с+с 2 + Определяем, где здесь квадраты чисел – это с 2 и 64=8 2 . Слагаемое –16с не может быть квадратом числа, так как оно отрицательное и степень числа с первая, поэтому –16с это удвоенное произведение чисел с и 8. Выполняем разложение на множители: –16с+с 2 +64=(с–8) 2 . Обратим внимание на тот момент, что числа с и 8 можно записывать наоборот в ответе, так как квадраты противоположных чисел равны, то есть –16с+с 2 +64=(8–с) 2

P.S. Все формулы на одной картинке:

Найдите значение выражения: (x + 5) 2 — x (x- 10) при x = — 1/20

В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:

(x + 5) 2 – x (x – 10) = x 2 + 2 • 5 • x + 25 – x 2 + 10x

Затем приведем подобные слагаемые:

x 2 + 2 • 5 • x + 25 – x 2 + 10x = 20 x + 25

Далее подставим x из условия:

20 x + 25 = 20 • (-1/20) + 25 = – 1 + 25 = 24

pазбирался: Даниил Романович | обсудить разбор | оценить

Разложение многочленов на множители с примерами решения

Содержание:

Разложение многочленов на множители

Разложение многочленов на множители — операция, об-I ратная умножению многочленов. Как вы уже знаете, решая разные задачи, иногда умножают два или более чисел, а иногда — раскладывают данное число на множители. Подобные задачи возникают и при преобразовании целых алгебраических выражений. В этой главе вы узнаете о:

• вынесении общего множителя за скобки;
• способе группировки;
• формулах сокращённого умножения;
• применении разных способов разложения многочленов на множители.

Вынесение общего множителя за скобки

Вы уже умеете раскладывать на множители натуральные числа. Например,

На множители раскладывают и многочлены. Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену. Например, многочлен

Один из способов разложения многочленов на множители — вынесение общего множителя за скобки. Рассмотрим его.

Каждый член многочлена ах + ау имеет общий множитель а. На основании распределительного закона умножения 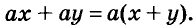Это означает, что данный многочлен ах + ау разложен на два множителя:

Чтобы убедиться, правильно ли разложен многочлен на множители, нужно выполнить умножение полученных множителей. Если всё верно, то в результате должен получиться данный многочлен.

Иногда приходится раскладывать на множители и выражения, имеющие общий многочленный множитель. Например, в выражении 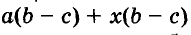общий множитель b — с. Его также можно выносить за скобки:

Один и тот же многочлен можно разложить на множители по-разному. Например,

Как правило, стараются вынести за скобки такой общий множитель, чтобы в скобках осталось простейшее выражение. Поэтому чаще всего в качестве коэффициента общего множителя берут наибольший общий делитель (НОД) коэффициентов всех членов данного многочлена или их модулей. Но не всегда. Все зависит от того, с какой целью раскладывают на множители многочлен.

Пусть, например, надо найти значение выражения 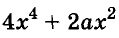при условии, когда

Чтобы использовать условие, это упражнение можно решить так:

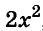
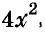
Здесь вынесено за скобки не , а тогда в скобках имеем выражение, значение которого известно из условия.

Пример:

Разложите на множители многочлен

Решение:

или

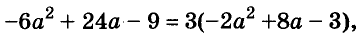
Пример:

Разложите на множители многочлен

Решение:

Пример:

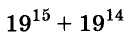
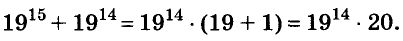
Докажите, что число делится на 20.

Последнее произведение делится на 20, поэтому делится на 20 и данная сумма.

Пример:

Решите уравнение

Решение:

поэтому данное уравнение равносильно уравнению Произведение двух чисел равно нулю тогда, когда хотя бы одно из них равно нулю.

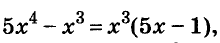
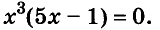
Значит, 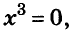отсюда х = 0, или 5х — 1 = 0, отсюда х = 0,2.

Ответ. Уравнение имеет два корня: 0 и 0,2.

Способ группировки

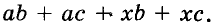
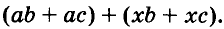
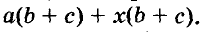
Разложим на множители многочлен Сгруппируем его члены так, чтобы слагаемые в каждой группе имели общий множитель Вынесем из первой группы за скобки общий множитель а, из второй — общий множитель х, получим выражение Слагаемые этого выражения имеют общий множитель b + с, вынесем его за скобки, получим выражение

Указанные преобразования можно записать цепочкой:

Такой способ разложения многочленов на множители называют способом группировки.

Замечание. Раскладывая на множители представленный выше многочлен, можно сгруппировать его члены иначе:

Получили такой же результат.

Разложим на множители многочлен

Записывать сумму а + с в виде 1 (а + с) необязательно, но сначала, чтобы не допускать ошибок, можно писать и так.

Чтобы воспользоваться способом группировки, иногда приходится один член данного многочлена представлять в виде суммы или разности одночленов. Чтобы разложить на множители трёхчлен 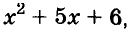• запишем одночлен

Подобные преобразования также можно выполнять, используя тождества.

Пример:

Разложите на множители многочлен:

Решение:

Ответ.

Пример:

Решите уравнение:

Решение:

Разложим левую часть уравнения на множители:

Корнем первого уравнения является у = 1,5, а второе уравнение корней не имеет, так как

Квадрат двучлена

Решая различные задачи, часто приходится умножать двучлены вида 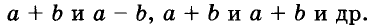Чтобы в таких случаях можно было сразу написать ответ, полезно запомнить тождества, которые называют формулами сокращённого умножения. Рассмотрим некоторые из них.

Умножим двучлен

Следовательно,

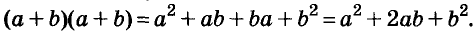
Квадрат двучлена равен квадрату первого его члена плюс удвоенное произведение первого на второй плюс квадрат второго члена.

Доказанное равенство — тождество, его называют формулой квадрата двучлена. Пользуясь ею, можно сразу записать:

Промежуточные преобразования желательно выполнять устно, тем самым сокращается запись:

По формуле квадрата двучлена можно возводить в квадрат любые двучлены, в том числе

Формулы квадрата двучлена используют и в «обратном направлении»:

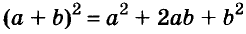
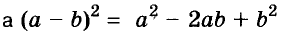
Формулу часто называют формулой квадрата суммы двух выражений, — квадрата разности двух выражений.

Для положительных чисел а и b формулу

можно доказать геометрически, как показано на рисунке 44. Так её доказывали ещё древние греки. Ведь площадь квадрата со стороной а + b равна сумме площадей квадратов а также прямоугольников ab и ab.

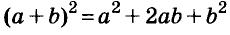
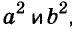
Существуют и другие формулы сокращённого умножения:

Пример:

Возведите в квадрат двучлен

Решение:

Пример:

Упростите выражение

Решение:

Пример:

Представьте в виде многочлена выражение:

Решение:

Пример:

Представьте выражение в виде степени двучлена:

Решение:

Разность квадратов

Умножим сумму переменных а и b на их разность.

Значит,

Это равенство — тождество. Словами его читают так:

Произведение суммы двух выражений и их разности равно разности квадратов этих выражений.

Пользуясь доказанной формулой, можно сразу записать:

Левую и правую части доказанной формулы можно поменять местами. Получим формулу разности квадратов двух выражений:

Разность квадратов двух выражений равна произведению их суммы и разности.

Пример:

Формула разности квадратов очень удобна для разложения многочленов на множители.

Для положительных чисел а и b формулу 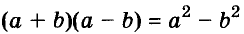можно проиллюстрировать геометрически (рис. 46). Но это тождество верно не только для положительных чисел, но и для любых других чисел и выражений.

Истинность формулы разности квадратов следует из правила умножения многочленов, а это правило — из законов действий сложения и умножения. Законы сложения и умножения чисел — это своеобразные аксиомы, следствиями которых являются алгебраические тождества.

Пример:

Напишите разность квадратов и квадрат разности выражений

Решение:

— разность квадратов; — квадрат разности данных выражений.

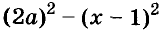
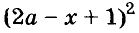
Пример:

Запишите в виде произведения двух двучленов выражение:

Решение:

Пример:

Представьте в виде двучлена выражение:

Решение:

.

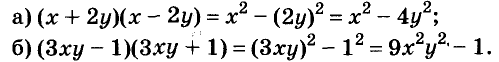
Используя формулу разности квадратов, промежуточные вычисления и преобразования можно выполнять устно, а записывать лишь конечный результат.

Использование формул сокращённого умножения

С помощью формул сокращённого умножения некоторые многочлены можно разложить на множители. Например, двучлен 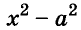можно представить в виде произведения по формуле разности квадратов:

Примеры:

Трёхчлены 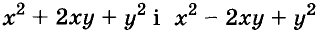раскладывают на множители по формуле квадрата двучлена:

Примеры:

Полученные, выражения можно разложить на множители и записать так:

Многочлен 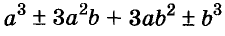можно разложить на множители по формуле куба двучлена:

Раскладывать на множители можно не только многочлены, но и некоторые другие целые выражения.

Например, 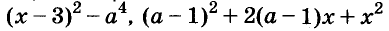— не многочлены, но и их можно представить в виде произведений многочленов:

Пример:

Разложите на множители многочлен:

Решение:

Пример:

Решите уравнение

Решение:

Значит, данное уравнение равносильно такому:

Квадрат числа равен нулю только тогда, когда это число равно 0. А х — 2 = 0, когда х = 2.

Пример:

Разложите на множители многочлен:

Решение:

Разность и сумма кубов

Выполним умножение многочленов

Следовательно, при любых значениях а и b

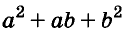
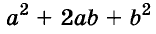
Трёхчлен называют неполным квадратом суммы выражений а и b (от он отличается только коэффициентом среднего члена). Поэтому доказанную формулу словами читают так:

разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

Выполним умножение многочленов

Трёхчлен 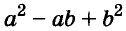называют неполным квадратом разности выражений а и b. Поэтому полученную формулу читаю так:

сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

С помощью доказанных формул можно раскладывать на множители многочлены, являющиеся разностями или суммами кубов.

Примеры:

Формулу «разность кубов» для положительных значений а и b можно проиллюстрировать геометрически, как показано на рисунке 49.

Если умножить на а — b выражения то получим формулы:

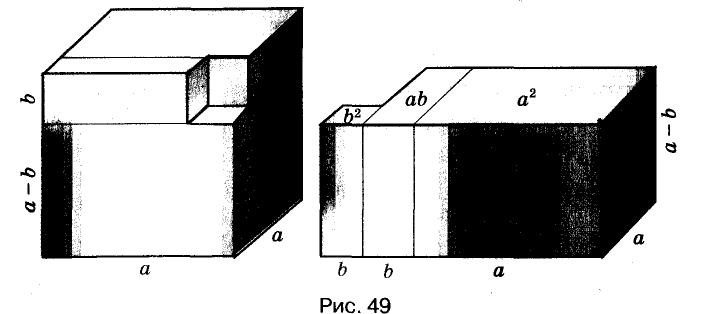
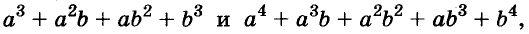
Можно доказать, что для каждого натурального значения n истинна формула:

Формулы «разность квадратов» и «разность кубов» — простейшие случаи этой общей формулы.

Пример:

Разложите на множители двучлен:

Решение:

Пример:

Найдите произведение многочленов: •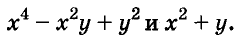

Решение:

Первый способ. По формуле суммы кубов:

Второй способ. По правилу умножения многочленов:

Применение разных способов разложения многочленов на множители

Чтобы разложить многочлен на множители, иногда приходится применять несколько способов.

Пример:

Разложите на множители многочлен

Решение:

Сначала за скобки вынесен общий множитель а, потом выражение в скобках разложено на множители по формуле разности квадратов.

Пример:

Разложите на множители выражение

Решение:

Здесь применены способ группировки, вынесение общего множителя за скобки и формула суммы кубов.

Чтобы разложить на множители более сложные многочлены, приходится применять несколько известных способов или искусственные приёмы.

В этом случае можно использовать такое правило-ориентир:

1. Вынести общий множитель (если он есть) за скобки.
2. Проверить, не является ли выражение в скобках разностью квадратов, разностью или суммой кубов.
3. Если это трёхчлен, то проверить, не является ли он квадратом двучлена.
4. Если многочлен содержит больше трёх членов, то надо попробовать группировать их и к каждой группе применить п. 1—3.

Иногда удаётся разложить многочлен на множители, прибавляя и вычитая из него одно и то же выражение.

Пример:

Разложите на множители двучлен

Решение:

Прибавим к данному двучлену выражение

Пример:

Разложите на множители выражение

Решение:

Пример:

Представьте многочлен 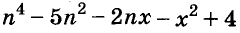в виде разности квадратов двух многочленов.

Решение:

Пример:

Докажите, что число 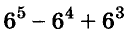делится на 31.

Последнее произведение делится на 31, поэтому делится на 31 и равное ему данное числовое выражение.

Исторические сведения:

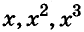
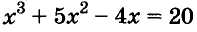
Наибольший вклад в развитие алгебраической символики внёс известный французский математик Ф. Виет, которого называли «отцом алгебры ». Он часто использовал буквенные обозначения. Вместо писал соответственно N,Q,C — первые буквы латинских слов Numerus (число), Quadratus (квадрат), Cubus (куб). Уравнение Ф. Виет записывал так:

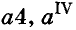
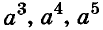
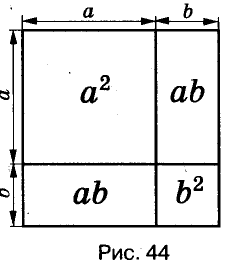
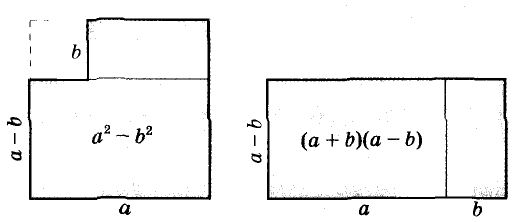
Степени чисел продолжительное время не имели специальных обозначений, четвёртую степень числа а записывали в виде произведения аааа. Позднее такое произведение начали записывать . Записи предложил Р. Декарт.

Формулы сокращённого умножения древним китайским и греческим математикам были известны за много веков до начала нашей эры. Записывали их тогда не с помощью букв, а словами и доказывали геометрически (только для положительных чисел). Пользуясь рисунком, объясняли, что для любых чисел а и b площадь квадрата со стороной а + b равна сумме площадей двух квадратов со сторонами а и b к двух прямоугольников со сторонами а, b. Итак, 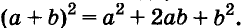Подобным способом обосновали и другие равенства, которые. мы теперь называем формулами сокращённого умножения.

В учебнике рассмотрены простейшие формулы сокращённого умножения.

Формулы квадрата и куба двучлена — простейшие случаи общей формулы бинома Ньютона:

Напомню:

Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену.

Простейшие способы разложения многочленов на множители:

• вынесение общего множителя за скобки;
• способ группировки;
• использование формул сокращённого умножения.

Примеры:

Формулы сокращённого умножения

Разложение многочленов на множители — это преобразование, обратное умножению многочленов. Схематично эти две операции можно изобразить, например, так.

• Системы линейных уравнений с двумя переменными
• Рациональные выражения
• Квадратные корни
• Квадратные уравнения
• Целые выражения
• Одночлены
• Многочлены
• Формулы сокращенного умножения

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.