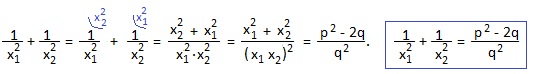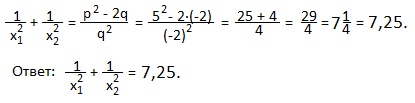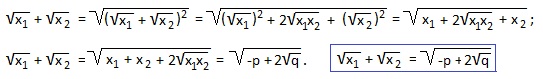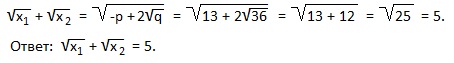Разность кубов корней квадратного уравнения

Иррациональные уравнения с кубическими радикалами

Разделы: Математика

Тема: «Иррациональные уравнения вида , .»

(Методическая разработка.)

Основные понятия

Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня (радикала) или знаком возведения в дробную степень.

Уравнение вида f(x)=g(x), где хотя бы одно из выражений f(x) или g(x) иррационально является иррациональным уравнением.

Основные свойства радикалов:

• Все радикалы четной степени являются арифметическими, т.е. если подкоренное выражение отрицательно, то радикал не имеет смысла (не существует); если подкоренное выражение равно нулю, то радикал тоже равен нулю; если подкоренное выражение положительно, то значение радикала существует и положительно.
• Все радикалы нечетной степени определены при любом значении подкоренного выражения. При этом радикал отрицателен, если подкоренное выражение отрицательно; равен нулю, если подкоренное выражение равно нулю; положителен, если покоренное выражение положительно.

Методы решения иррациональных уравнений

Решить иррациональное уравнение – значит найти все действительные значения переменной, при подстановке которых в исходное уравнение оно обращается в верное числовое равенство, либо доказать, что таких значений не существует. Иррациональные уравнения решаются на множестве действительных чисел R.

Областью допустимых значений уравнения состоит из тех значений переменной, при которых неотрицательны все выражения, стоящие под знаком радикалов четной степени.

Основными методами решения иррациональных уравнений являются:

а) метод возведения обеих частей уравнения в одну и ту же степень;

б) метод введения новых переменных (метод замен);

в) искусственные приемы решения иррациональных уравнений.

В данной статье остановимся на рассмотрении уравнений определённого выше вида и приведём 6 методов решения таких уравнений.

1 метод. Возведение в куб.

Этот способ требует применения формул сокращённого умножения и не содержит «подводных» камней, т.е. не приводит к появлению посторонних корней.

Пример 1. Решить уравнение

Перепишем уравнение в виде и возведём в куб обе его части. Получим уравнение равносильное данному уравнению ,

,

,

Пример 2. Решить уравнение .

Перепишем уравнение в виде и возведём в куб обе его части. Получим уравнение равносильное данному уравнению

,

,

,

и рассмотрим полученное уравнение как квадратное относительно одного из корней

,

,

следовательно, дискриминант равен 0,а уравнение может иметь решение х=-2.

Проверка:

Замечание: Проверка может быть опущена, в том случае, если дорешивается квадратное уравнение.

2 метод. Возведение в куб по формуле.

По-прежнему будем возводить уравнение в куб, но при этом пользоваться модифицированными формулами сокращенного умножения.

,

(незначительная модификация известной формулы), тогда

Пример3. Решить уравнение .

Возведём уравнение в куб с использованием формул, приведённых выше.

,

Но выражение должно быть равно правой части. Поэтому имеем:

, откуда

.

Теперь при возведении в куб получаем обычное квадратное уравнение:

, и два его корня

,

Оба значения, как показывает проверка, правильные.

Но все ли преобразования здесь равносильны? Прежде чем ответить на этот вопрос, решим ещё одно уравнение.

Пример4. Решить уравнение .

Возводя, как и ранее, обе части в третью степень, имеем:

.

Откуда (учитывая, что выражение в скобках равно ), получаем:

, значит

. Получаем, .Сделаем проверку и убедимся х=0 –посторонний корень.

Ответ: .

Ответим на вопрос: «Почему возникли посторонние корни?»

Равенство влечёт равенство . Заменим с на –с, получим:

и .

Нетрудно проверить тождество

,

Итак, если , то либо , либо . Уравнение можно представить в виде , .

Заменяя с на –с, получаем: если , то либо , либо

Поэтому при использовании этого метода решения обязательно нужно сделать проверку и убедиться что посторонних корней нет.

3 метод. Метод системы.

Пример 5. Решить уравнение .

Введём замену, составим и решим систему уравнений.

Пусть , . Тогда:

откуда очевидно, что

Второе уравнение системы получается таким образом, чтобы линейная комбинация подкоренных выражений не зависела от исходной переменной.

Легко убедиться , что система не имеет решения, следовательно и исходное уравнение не имеет решения.

Ответ: Корней нет.

Пример 6. Решить уравнение .

Введём замену, составим и решим систему уравнений.

Пусть , . Тогда

или

Возвращаясь к исходной переменной имеем:

х=0.

4 метод. Использование монотонности функций.

Прежде чем использовать данный метод обратимся к теории.

Нам понадобятся следующие свойства:

• Если функции y=f(x) и y=g(x) возрастают (убывают) на некотором множестве, то функция y=f(x)+g(x) также возрастает (убывает ) на этом множестве.
• Если функции y=f(x) и y=g(x) возрастают (убывают) на некотором множестве, при чем обе они принимают неотрицательные значения при всех допустимых х, то функция y=f(x)g(x) возрастает (убывает) на данном множестве.
• Если функция y=f(x) монотонная, то уравнение f(x)=a имеет не более одного решения.
• Если функции y=f(x) и y=g(x) имеют разный характер монотонности, то уравнение f(x)=g(x) имеет не более одного решения.
• Функция вида возрастает при к>0 и убывает при к 30.05.2009

8.2.4. Применение теоремы Виета

Часто требуется найти сумму квадратов (x₁ 2 +x₂ 2 ) или сумму кубов (x₁ 3 +x₂ 3 ) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения:

Помочь в этом может теорема Виета:

Сумма корней приведенного квадратного уравнения x 2 +px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Выразим через p и q:

1) сумму квадратов корней уравнения x 2 +px+q=0;

2) сумму кубов корней уравнения x 2 +px+q=0.

Решение.

1) Выражение x₁ 2 +x₂ 2 получится, если взвести в квадрат обе части равенства x₁+x₂=-p;

(x₁+x₂) 2 =(-p) 2 ; раскрываем скобки: x₁ 2 +2x₁x₂+ x₂ 2 =p 2 ; выражаем искомую сумму: x₁ 2 +x₂ 2 =p 2 -2x₁x₂=p 2 -2q. Мы получили полезное равенство: x₁ 2 +x₂ 2 =p 2 -2q.

2) Выражение x₁ 3 +x₂ 3 представим по формуле суммы кубов в виде:

Еще одно полезное равенство: x₁ 3 +x₂ 3 =-p·(p 2 -3q).

Примеры.

3) x 2 -3x-4=0. Не решая уравнение, вычислите значение выражения x₁ 2 +x₂ 2 .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения

x₁+x₂=-p=3, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 1) равенство:

x₁ 2 +x₂ 2 =p 2 -2q. У нас -p=x₁+x₂=3 → p 2 =3 2 =9; q=x₁x₂=-4. Тогда x₁ 2 +x₂ 2 =9-2·(-4)=9+8=17.

4) x 2 -2x-4=0. Вычислить: x₁ 3 +x₂ 3 .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения x₁+x₂=-p=2, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 2) равенство: x₁ 3 +x₂ 3 =-p·(p 2 -3q)=2·(2 2 -3·(-4))=2·(4+12)=2·16=32.

Ответ: x₁ 3 +x₂ 3 =32.

Вопрос: а если нам дано не приведенное квадратное уравнение? Ответ: его всегда можно «привести», разделив почленно на первый коэффициент.

5) 2x 2 -5x-7=0. Не решая, вычислить: x₁ 2 +x₂ 2 .

Решение. Нам дано полное квадратное уравнение. Разделим обе части равенства на 2 (первый коэффициент) и получим приведенное квадратное уравнение: x 2 -2,5x-3,5=0.

По теореме Виета сумма корней равна 2,5; произведение корней равно -3,5.

Решаем так же, как пример 3), используя равенство: x₁ 2 +x₂ 2 =p 2 -2q.

x₁ 2 +x₂ 2 =p 2 -2q=2,5 2 -2∙(-3,5)=6,25+7=13,25.

Ответ: x₁ 2 +x₂ 2 =13,25.

6) x 2 -5x-2=0. Найти:

Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x₁ 2 +x₂ 2 =p 2 -2q.

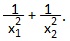
В нашем примере x₁+x₂=-p=5; x₁∙x₂=q=-2. Подставляем эти значения в полученную формулу:

7) x 2 -13x+36=0. Найти:

Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.

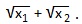
У нас x₁+x₂=-p=13; x₁∙x₂=q=36. Подставляем эти значения в выведенную формулу:

Совет: всегда проверяйте возможность нахождения корней квадратного уравнения по подходящему способу, ведь 4 рассмотренные полезные формулы позволяют быстро выполнить задание, прежде всего, в тех случаях, когда дискриминант — «неудобное» число. Во всех простых случаях находите корни и оперируйте ими. Например, в последнем примере подберем корни по теореме Виета: сумма корней должна быть равна 13, а произведение корней 36. Что это за числа? Конечно, 4 и 9. А теперь считайте сумму квадратных корней из этих чисел: 2+3=5. Вот так то!

«10 класс Первый тур (10 минут; каждая задача – 6 баллов). 1.1. Известно. что разность кубов корней квадратного уравнения ax2 + bx + c . »

Первый тур (10 минут; каждая задача – 6 баллов).

1.1. Известно. что разность кубов корней квадратного уравнения ax2 + bx + c = 0 равна

2011. Сколько корней имеет уравнение ax2 + 2bx + 4c = 0?

Ответ: два корня.

Из условия задачи следует, что уравнение ax2 + bx + c = 0 имеет два корня.

Следовательно, его дискриминант D = b2 – 4ac 0. Упрощенный дискриминант уравнения

ax2 + 2bx + 4c = 0 также равен b2 – 4ac, значит оно также имеет два корня.

1.2. Точки K и L – середины сторон АВ и ВС правильного шестиугольника АВСDEF.

Отрезки KD и LE пересекаются в точке М. Площадь треугольника DEM равна 12. Найдите площадь четырехугольника KBLM. Рис. 1 Ответ: 12.

Так как четырехугольник KBCD является образом четырехугольника LCDE при повороте вокруг центра АВСDEF на угол 60, то эти четырехугольники равны, а значит, и равновелики (см. рис. 1). Вычитая из площади каждого из них площадь четырехугольника LCDM, получим, что S KBLM S DEM = 12.

1.3. Найдите наименьшее число, кратное 45, десятичная запись которого состоит только из единиц и нулей.

Число кратно 45, если оно кратно каждому из двух взаимно простых чисел: 9 и 5. Так как искомое число делится на 9, то его сумма цифр должна делится на 9. Следовательно, количество единиц в искомом числе кратно девяти. Число, кратное пяти, может оканчиваться на 0 или на 5, но второй случай невозможен по условию. Таким образом, учитывая, что искомое число должно быть наименьшим, оно должно содержать 9 единиц и оканчиваться нулем.

Второй тур (15 минут; каждая задача – 7 баллов).

2.1. Функция f(x) определена для всех x, кроме 1, и удовлетворяет равенству:

x 1 x 1 f x f x. Найдите f(–1).

Подставим в данное равенство значения x = 0 и x = –1. Получим:

f 1 f 0,. Следовательно, 2 f 1 1 f 1, то есть f 1 = –1.

2 f 0 1 f 1 Отметим, что можно решить и более общую задачу: найти f(x) для всех значений x 1 x 1. Действительно, заменим в исходном равенстве х на. Получим, что x 1 x 1 x 1 x 1 1 x 1 x 1 x 1 x 1 x 1 x 1 1 f x 1 x 1 f x 1 x 1 f x x 1 f x 1 = f

+88 = 2(x – 6,5)2 + 1,75 0, то CM2 + CD2 MD2, значит, угол DCM – острый, что и требовалось.

2.3. В шахматном турнире участвовало 8 человек и в итоге они набрали разное количество очков (каждый играл с каждым один раз, победа – 1 очко, ничья – 0,5 очка, поражение – 0). Шахматист, занявший второе место, набрал столько же очков, сколько четверо последних набрали вместе. Как сыграли между собой шахматисты, занявшие третье и седьмое место?

Ответ: выиграл шахматист, занявший третье место.

Заметим, что занявшие четыре последних места, сыграли друг с другом 6 партий, разделив между собой 6 очков. Поэтому, у шахматиста, занявшего второе место, не может быть менее шести очков.

Докажем, что более шести очков у него быть не может. Действительно, 6,5 или 7 очков у него может быть только в одном случае: если он выиграл у всех игроков, занявших более низкие места, и не проиграл победителю, но тогда количество очков победителя турнира будет не больше, чем у занявшего второе место.

Полученное противоречие показывает, что шахматист, занявший второе место, набрал ровно 6 очков, значит, игроки, занявшие четыре последних места, проиграли все партии игрокам, занявшим места выше них.

Третий тур (20 минут; каждая задача – 8 баллов).

3.1. Найдите наименьшее значение x2 + y2, если x2 – y2 + 6x + 4y + 5 = 0.

Преобразуем исходное равенство: x – y + 6x + 4y + 5 = 0 (x + 6x + 9) – (y – 4y + 4) = 0 (x + 3)2 – (y – 2)2 = 0 (x + y + 1)(x – y + 5) = 0. Далее можно рассуждать поразному.

Первый способ. Рассмотрим график полученного уравнения и найдем на нем точку, для которой выражение x2 + y2 принимает наименьшее значение. Так как полученное уравнение равносильно совокупности y x 1, y x 5, то его графиком является объединение двух

= (x2 – xy + y2)(x6 – x3y3 + y6).

Полученные множители имеют одинаковый вид (неполный квадрат суммы). Но a2 – ab + b2 = (a – b)2 + ab 1, если а и b – натуральные числа. Равенство возможно только при x = y = 1, тогда данное число равно 1, то есть не является простым. В остальных случаях каждый множитель больше 1, поэтому, данное число является составным.

5.2. Дан угол с вершиной O и окружность, касающаяся его сторон в точках A и B. Луч с началом в точке A, параллельный OB, пересекает окружность в точке C. Отрезок OC пересекает окружность в точке E. Прямые AE и OB пересекаются в точке K. Докажите, что OK = KB.

Пусть ACE =, тогда OAK = (угол между касательной и хордой, см. рис. 7), и EOK = (CA || OB). Следовательно, треугольники AOK и OEK OK AK OK2 = AKEK.

подобны, значит, EK OK С другой стороны, по свойству касательной и секущей, проведенных из одной точки, KВ2 = KАKЕ. Таким образом, OK = KB, что и требовалось.

Равенство OK2 = AKEK можно также получить из других соображений. Рассмотрим окружность, описанную около треугольника АЕО и касательную к ней в точке Рис. 7 О (см. рис. 7). Тогда из равенства углов OAE и EOK следует, что эта касательная совпадает с прямой ОВ. Применив для построенной окружности и точки K свойство касательной и секущей, получим требуемое равенство.

5.3. Сумма номеров домов на одной стороне квартала равна 247. Какой номер имеет седьмой дом от угла?

Пусть первый от угла дом квартала имеет номер р, а количество домов на одной стороне квартала равно k. Тогда, последовательность р, р + 2, р + 4. р + 2(k – 1) номеров этих домов является арифметической прогрессией. Сумма первых k членов этой p p 2k 2 прогрессии равна k = (р + k – 1)k.

По условию получим уравнение: (р + k – 1)k = 247. Разложение на простые множители числа 247 имеет вид 247 = 1319. Так как р 1, то р + k – 1 k, значит, р + k – 1 = 19, а k = 13, то есть р = 7. Следовательно, на одной стороне квартала 13 домов, а их нумерация начинается с числа 7. Таким образом, седьмой дом (от любого угла) имеет

«DOMESTIC VIOLENCE AS A MEDICAL AND SOCIAL PROBLEM Boryack Victor Petrovich, DSc of Medical science, Professor, Chair of Social Work and Social Rights, Russian State Social University (branch), Director – chief medical officer sanatorium Rodnik, Pyatigorsk Chobanyan Emma Yurevna, Student. »

«Ю. А. Комарова ОБЪЕКТИВНОСТЬ КАК ВАЖНЫЙ СТИЛЕОБРАЗУЮЩИЙ ФАКТОР НАУЧНОЙ РЕЧИ НА АНГЛИЙСКОМ ЯЗЫКЕ Научная речь на английском языке характеризуется своими особыми чертами. Объективность изложения является важным стилеобразующим фактором научной речи. Названный признак реализуется через четкую и лингв. »

«Черепанов Игорь Владимирович ПРОБЛЕМА БЫТИЯ СОЗНАНИЯ КАК СУБЪЕКТИВНОЙ ЦЕЛОСТНОСТИ В ОБЪЕКТИВНО СУЩЕСТВУЮЩЕМ МИРЕ В статье анализируются философские теории, позволяющие решить проблему бытия сознания как субъективной целостности в объективно существующем мире. Рассматривается феномен сознания со ст. »

«Жунал «Connect! Мир связи» – №10, октябрь 2007 КОНВЕРГЕНЦИЯ ТЕХНОЛОГИЙ В ОПЕРАТОРСКИХ СЕТЯХ. СЦЕНАРИИ ВОЗМОЖНЫЕ И НЕВОЗМОЖНЫЕ Борис Гольдштейн, Александр Гольдштейн, д. т. н., проф., зав. кафедрой к. »

«БЛИЖНИЙ ВОСТОК И АФРИКА А.Г. НЕСТЕРОВ ТЮМЕНСКОЕ ХАНСТВО: ГОСУДАРСТВО СИБИРСКИХ ШЕЙБАНИДОВ В X V в. В конце XIV в. территория Урала и Западной Сибири находилась, по-видимому, во владении Гийас ад-дин Тохтамыш хана; по крайней мере, Ан. »

«Устав Профсоюза работников народного образования и науки Российской Федерации 1. ОБЩИЕ ПОЛОЖЕНИЯ 1. Профессиональный союз работников народного образования и науки Российской Федерации (далее именуется «Профсоюз») является добровольным общественным объединением граждан, работающих в образовательных учреждениях. »

«УДК 316.614-058.862 С. В. Панкратова Панкратова С. В.СОЦИАЛЬНЫЙ КАПИТАЛ КАК ИНСТРУМЕНТ УСПЕШНОЙ СОЦИАЛЬНОЙ АДАПТАЦИИ ДЕТЕЙ-СИРОТ И ДЕТЕЙ, ОСТАВШИХСЯ БЕЗ ПОПЕЧЕНИЯ РОДИТЕЛЕЙ Социальный капитал как инструмент успешной социальной адаптации детей-си. »

2017 www.doc.knigi-x.ru — «Бесплатная электронная библиотека — различные документы»

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.