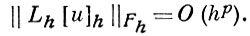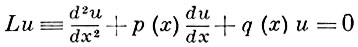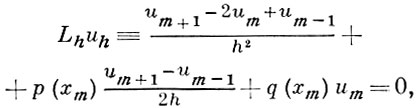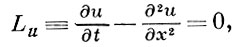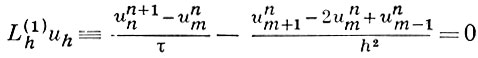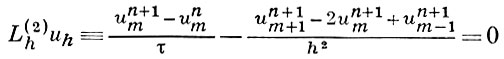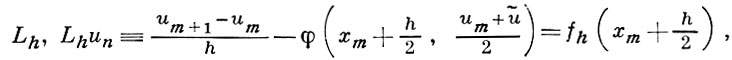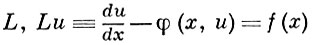Разностная схема аппроксимирует дифференциальное уравнение

АППРОКСИМАЦИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ РАЗНОСТНЫМ

Расстановка ударений: АППРОКСИМА`ЦИЯ ДИФФЕРЕНЦИА`ЛЬНОГО УРАВНЕ`НИЯ РА`ЗНОСТНЫМ

АППРОКСИМАЦИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ РАЗНОСТНЫМ — приближение дифференциального уравнения системой алгебраич. уравнений относительно значений искомых функции на нек-рой сетке, к-рое уточняется при стремлении параметра (шага сетки) к нулю.

Пусть L, Lu = f нек-рый дифференциальный оператор, a L_h, L_h u_h = f_h, u_h ∈ U_h, f_h ∈ F_h — нек-рый разностный оператор (см. Аппроксимация дифференциального оператора разностным). Говорят, что разностное уравнение L_h u_h = 0, 0 ∈ F_h аппроксимирует дифференциальное уравнение Lu = 0 на решении u с порядком h p , если оператор L_h аппроксимирует оператор L на решении u с порядком р, т. е. если

Простейший пример построения разностного уравнения L_h u_h = 0, аппроксимирующего дифференциальное уравнение Lu = 0 на решениях и, состоит в замене каждой производной, входящей в выражение Lu, аппроксимирующим ее разностным аналогом.

аппроксимируется со 2-м порядком разностным уравнением

где сетки D_hU и D_hF состоят из точек x_m = mh, m — целое, u_m — значение функции u_h в точке x_m ; для уравнения

напр., двумя различными разностными аппроксимациями на гладких решениях являются:

(неявная схема), где сетки D_hU и D_hF состоят из точек (х_m, t_n) = (mh, nτ), τ = rh 2 , r = const, m и n — целые, а u n _m— значение функции u_h в точке (х_m, t_n) сетки. Существуют разностные операторы L_h, аппроксимирующие дифференциальный оператор L особенно хорошо только на решениях u уравнения Lu = 0 и хуже на других функциях. Напр., оператор

где ũ = u_m+ hφ (x_m) аппроксимирует оператор на

произвольных гладких функциях u(х) с первым порядком относительно h, а на решениях уравнения Lu = 0 со вторым [функция u(х) предполагается достаточно гладкой]. При численном решении краевых задач для дифференциального уравнения Lu = 0 с помощью разностного уравнения L_h u_h = 0 существенны свойства аппроксимации оператора L оператором L_h на решениях u уравнения Lu = 0, а не на произвольных гладких функциях. Для широкого класса дифференциальных уравнений и систем уравнений существуют способы построения аппроксимирующих их разностных уравнений, при к-рых выполняются различные дополнительные требования: устойчивость решения u_h относительно ошибок округления, допускаемых при вычислениях; выполнение для u_h тех или иных интегральных соотношений, имеющих место для решения u дифференциального уравнения; возможность использовать произвольные сетки D_hu и D_hF (важная при расчете движения сплошной среды); малое число арифметич. действий, необходимых для вычисления решения, и т. д.

А. д. у. р. является элементом аппроксимации дифференциальной краевой задачи разностной с целью приближенного вычисления решения первой.

Лит. : [1] Годунов С. К., Рябенький В. С., Введение в теорию разностных схем, М., 1962; [2] Самарский А. А., Введение в теорию разностных схем, М., 1971; [3] Годунов С. К. и др., Численное решение многомерных задач газовой динамики, М., 1976; [4] Самарский А. А., Попов Ю. П., Разностные схемы газовой динамики, М., 1975.

1. Математическая Энциклопедия. Т. 1 (А — Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] — М., «Советская Энциклопедия», 1977, 1152 стб. с илл.

Сходимость. Аппроксимация. Устойчивость

Эти основные понятия теории разностных схем уже обсуждались при построении численных методов для решения обыкновенных дифференциальных уравнений. При переходе к уравнениям с частными производными качественно меняется характер рассматриваемых задач, поэтому необходимо снова рассмотреть эти понятия. Разумеется, мы не имеем здесь возможности изложить теорию разностных схем, но попытаемся привести самые необходимые сведения.

Исходную дифференциальную задачу,состоящую в решении уравнения с частными производными при заданных начальных и граничных условиях, запишем в операторном виде:

(2.7)

Заметим, что это операторное уравнение включает не только исходное уравнение с частными производными, но и дополнительные (начальные и граничные) условия. Функция F(x, t) описывает правые части уравнения, а также начальные и граничные условия. Область включает расчетную область Gи границу Г.

Дифференциальную задачу (2.7) заменяем разностной задачей относительно сеточной функции uh, определенной в узлах сетки . Для простоты будем считать, что сетка зависит от одного параметра h, а шаг по времени τ выражается через h: τ = rh, где r = const. Разностную задачу можно также записать в операторном виде:

(2.8)

Значения сеточной функции в узлах сетки приближенно заменяют значения искомой функции в тех же узлах с погрешностями:

(2.9)

Введем некоторое характерное значение этих погрешностей, например их максимальное по модулю значение на сетке

.

Разностная схема (2.8) называется сходящейся,если при сгущении узлов сетки это значение погрешности стремится к нулю, т.е. если

Если при этом , где М = const > 0, то разностная схема имеет k—ый порядок точности. Говорят также, что она сходится со скоростью O(hk).

Можно ввести понятие порядка точности и для случая независимых параметров сетки h, τ. В частности, при выполнении условия разностная схема сходится со скоростью и имеет р-ый порядок точности по hи q-ый порядок по τ.

Определим сеточную функцию погрешности δhкак разность между решением дифференциальной задачи, рассматриваемом в узлах сетки, и разностным решением: . При этом значение δhв узле с номером (i, j)определяется соотношением (2.9). Выразим uh, через Uhи δhи подставим в уравнение (2.8). Имеем

(2.10)

Величина Rhназывается невязкой (погрешностью аппроксимации) разностной схемы. Она равна разности между левой и правой частями (2.8) при подстановке в это уравнение решения дифференциальной задачи (2.7).

Введем некоторую характерную величину невязки R,например

Тогда при R = O(hk) аппроксимация имеет k-ый порядок относительно h. Если значения h и τ независимы, то при порядок аппроксимации разностной схемы р-ыйпо пространству и q—ыйпо времени.

Разностная схема (2.8) аппроксимирует исходную дифференциальную задачу (2.7), если при измельчении сетки невязка стремится к нулю, т.е.

Аппроксимация такого типа, т.е. когда невязка стремится к нулю при стремлении к нулю h и τ по любому закону без каких-либо условий, называется безусловной или абсолютной аппроксимацией. В случае условной аппроксимации накладываются некоторые условия на размеры шагов по пространству и времени. Например, если , то R→ 0 при и , т.е. разностная задача аппроксимирует исходную при условии, что τ стремится к нулю быстрее, чем h2. Так, при t = h2аппроксимация в данном примере отсутствует.

Разностная схема (2.8) называется устойчивой,если ее решение непрерывно зависит от входных данных, т.е. малому изменению входных данных соответствует малое изменение решения. Устойчивость характеризует чувствительность разностной схемы к различного рода погрешностям. Она является внутренним свойством разностной задачи, и это свойство не связывается непосредственно с исходной дифференциальной задачей (в отличие от сходимости и аппроксимации).

По аналогии с аппроксимацией устойчивость бывает условной и безусловной в зависимости от того, накладываются или нет ограничения на соотношения между шагами по разным переменным.

В теории разностных схем рассматриваются разные способы исследования аппроксимации исходной дифференциальной и разностной задач и проверки устойчивости разностных схем. Здесь мы лишь отметим, что эти исследования значительно проще, чем доказательство сходимости разностного решения к точному. Поэтому пользуются следующим утверждением.

Теорема. Если решение исходной дифференциальной задачи (2.7) существует, а разностная схема (2.8) устойчива и аппроксимирует задачу (2.7) на данном решении с порядком k, то разностное решение сходится к точному со скоростью O(h(k)).

Короче говоря, из аппроксимации и устойчивости следует сходимость. Поэтому, доказав аппроксимацию и устойчивость разностной схемы, можем быть уверены в ее сходимости.

Проиллюстрируем исследование разностных схем на примере рассмотренных выше двух схем для уравнения теплопроводности — явной схемы (2.3) и неявной схемы (2.4). Будем считать, что решение U(x,t) дифференциальной задачи (2.2) существует, а частные производные ¶2U/¶t2и ¶4U/¶x4 непрерывны и ограничены в расчетной области. Тогда в соответствии с формулами численного дифференцирования для каждого узла можно написать следующие соотношения:

;

. (2.11)

Найдем погрешность аппроксимации исходного уравнения (2.2) с помощью разностной схемы (2.3) для произвольного узла сетки :

.

Подставим в это равенство соотношения (2.11). При этом заметим, что поскольку U(x, t) является точным решением уравнения (2.2), то

(2.12)

Следовательно, максимальное значение невязки с учетом (2.11), (2.12) имеет порядок

Аналогичную оценку невязки можно получить и для разностной схемы (2.4).

Таким образом, разностные схемы (2.3) и (2.4) аппроксимируют исходное дифференциальное уравнение (2.2) со вторым порядком по h и с первым порядком по τ. Начальное и граничные условия задачи (2.2) аппроксимируются на границах точно, поскольку здесь значения сеточной функции равны значениям решения: Г – граница расчетной области (t= 0, х = 0, х = 1).

Исследуем теперь устойчивость данных разностных схем. Начнем с явной схемы (2.3) при граничных условиях (2.5) и начальном условии (2.6). Найдем из (2.3) значение сеточной функции на верхнем слое:

(2.13)

Допустим, что имеет место ограничение в виде неравенства

(2.14)

Тогда . Эти соотношения используем для оценки сеточного решения (2.13):

(2.15)

Введем теперь обозначение для наибольшего по модулю значения сеточной функции на j—омслое

и с учетом граничных условий (2.5) запишем неравенство (2.15) для значений решения на всем (j+ 1)-ом слое, включая границы:

. (2.16)

Отсюда при j= 0 получаем

(2.17)

Из (2.5), (2.6) следует, что

поэтому неравенство (2.17) можно записать в виде

(2.18)

При j= 1 из (2.16), (2.18) получаем

Аналогично, для некоторого j = Jимеем

(2.19)

Таким образом, значения сеточного решения на (J + 1)-ом слое не превосходят по модулю известных значений сеточного решения на нулевом слое (j= 0) и на границах i= 0, i = I[по (J+1)-ый слой включительно].

Неравенство (2.19) означает устойчивость разностной схемы (2.3). Покажем это. Разностная схема была выше названа устойчивой, если малому изменению входных данных соответствует малое изменение решения. Рассмотрим разностную задачу, входные данные которой, например начальное условие, подверглись малому изменению :

(2.20)

Решением этой задачи будет сеточная функция

(2.21)

где — решение исходной разностной задачи (2.3), (2.5), (2.6), а — некоторая поправка к решению. Подставим (2.21) в (2.20):

Отсюда с учетом (2.3), (2.5), (2.6) получаем разностную задачу относительно поправки

Эта задача совпадает с исходной, но при других начальных и граничных условиях. К ее решению применимо неравенство (2.19), которое в данном случае имеет вид и означает малость поправки к решению при малом изменении начального условия. Таким образом, схема (2.3) устойчива при выполнении условия (2.14). Можно показать, что при нарушении этого условия схема (2.3) будет неустойчивой, т.е. явная схема (2.3) условно устойчива. Из аппроксимации и устойчивости следует ее сходимость со скоростью O(h2+τ).

Исследуем теперь устойчивость неявной разностной схемы (2.4). Запишем, с помощью (2.4), (2.5) систему уравнений для нахождения неизвестных значений сеточной функции на верхнем слое:

(2.22)

Эта система может быть решена методом прогонки. Безусловная устойчивость неявной схемы (2.4) обеспечивается выполнением условий устойчивости метода прогонки для системы (2.22).

Устойчивость и сходимость разностных схем можно оценить путем расчетов с измельчением сетки . Однако это приводит к существенному увеличению объема вычислений и возрастанию суммарных погрешностей.

Многолетняя практика использования численных методов для решения инженерных задач на компьютерах показывает, что применение той или иной разностной схемы, даже если она исследована теоретически, требует ее тщательной апробации при решении конкретной задачи. Для этого проводятся методические вычислительные эксперименты, состоящие в расчетах с разными значениями шагов при разных исходных данных. Полезно также отладить методику с помощью тестовых задач, для которых либо удается получить аналитическое решение, либо имеется численное решение, найденное другим численным методом.

Аппроксимация дифференциальных уравнений

В основе методов численного решения дифференциальных уравнений, лежит преобразование дифференциальной задачи в разностную задачу, называемое аппроксимацией. Простыми словами: чтобы решить дифференциальные уравнения нужно знать аппроксимацию дифференциальных уравнений.

Но перед тем, как мы приступим к рассмотрению дифференциального уравнения, сначала разберем аппроксимацию дифференциальных операторов, то есть производных первого и второго порядков.

Аппроксимация дифференциальных операторов

Рассмотрим производную функции u(x) в точке x_j:

Аппроксимация этой производной может быть введена с помощью следующих разностных операторов:

с помощью правой конечной разности

с помощью левой конечной разности

с помощью центральной конечной разности

У каждой из этих разностей есть так называемый порядок аппроксимации.

Аппроксимация — это, по сути, приближение к реальному результату. Порядок же аппроксимации показывает порядок ошибки при этом приближении. Вот вам пример:
реальный ответ в задачи : 5
аппроксимация первого порядка показала ответ : 5.8
аппроксимация второго порядка показала ответ : 5.08

Исходя из этого, мы можем сделать совершенно простой вывод, что чем больше порядок аппроксимации, тем лучше сама аппроксимация той задачи, которая решается.

Возвращаясь к нашим разностям, отметим что левая и правая конечные разности имеют 1 порядок аппроксимации, а центральная конечная разность имеет 2 порядок аппроксимации. Значит центральная разность считает точнее, но не всегда удается использовать именно эту конечную разность, но об этом мы поговорим в следующих статьях.

Далее нам следует рассмотреть конечную разность для производной второго порядка:

она запишется следующим образом :

Пока вам все это может показаться непонятным и не самым интересным, но со временем вы это действительно поймете и будете экспертом в этой области.

Аппроксимация дифференциальных уравнений

Ну а теперь нам пора перейти к более сложному, но в тоже время важному занятию.
Рассмотрим одномерное дифференциальное уравнение параболического типа:(если вы забыли, что это, то советую повторить это вот здесь)

В левой части стоит первая производная по времени, и ее можно аппроксимировать левой, правой или центральной конечной разностью, для примера мы возьмем левую.

В правой части стоит вторая производная по координате x, ее аппроксимируем разностью, которую рассматривали для производной второго порядка.

Свободный член так и останется.

В итоге после аппроксимации уравнение станет выглядеть вот так:

Это выражение называется разностной схемой. По правде говоря, это еще не полная разностная схема, но пока что вам нужно понять основы аппроксимации и выучить понятие порядка аппроксимации.

Для этой статьи, пожалуй, хватит. В следующих статьях мы подробнее изучим разностные схемы, а затем будем их программировать на языках C++ и VBA.