Разностная схема для дифференциального уравнения второго порядка

Разностные схема для обыкновенных дифференциальных уравнений второго порядка с сингулярными точками Текст научной статьи по специальности « Математика»

Похожие темы научных работ по математике , автор научной работы — Джураев Хайрулло Шарофович, Наджмиддинов Асадулло Мирзоевич

Текст научной работы на тему «Разностные схема для обыкновенных дифференциальных уравнений второго порядка с сингулярными точками»

Разностные схема для обыкновенных дифференциальных уравнений второго порядка с сингулярными точками

Джураев Хайрулло Шарофович,

к.ф.м.н., доцент, зав.кафедры вычислительные машины, системы и сетей Таджикский национальный университет. e-mail: hayrullo_58@mail.ru

Наджмиддинов Асадулло Мирзоевич,

аспирант кафедры вычислительные машины, системы и сетей Таджикский национальный университет. e-mail: asadullo-tj@mail.ru

В работе предлагается разностный метод нахождения приближенного решения двухточечные граничных задач для обыкновенных дифференциальных уравнений второго порядка с сингулярными точками. Следующее обстоятельство важно для практического использования предложенной схемы, так как в теоретических и практических задачах значения коэффициентов мало, то есть x — a. В этом случае искомая функция u(x, /и) резко меняется для малых X — a , что,

казалось бы, должно повлечь необходимость существенного измельчения сетки в этой области. При построении разностной схемы учитывается поведение выражение /и du . Это дает возможность

решать задачу с очень малыми x — a , беря практически вполне приемлемый h. В математической постановке прикладных задач возникает поведения решений при значениях коэффициентах. В связи с этом утверждается, что разностная схема аппроксимирует

семейство задач с точностью O(h2) в класс решений C(4) (a,b) обыкновенных дифференциальных уравнения второго порядка с сингулярными точками с двухточечными граничными условиями. В работе доказывается, что решение разностной аппроксимации задачи имеет свойством не отрицательность, а ограниченность, устойчивость. Устойчивость и сходимость разностных схем можно оценить путем расчетов с измельчением сетки.

Ключевые слова: дифференциальное уравнение, граничных задач, разностная схема, сингулярные точки, сеточной области, узлы, приемлемы шаг, трёхдиагональная симметричная матрица.

Математических моделирование распространения тепло в твердом теле при наличии источников тепло описывается двухточечные граничные задачи для обыкновенного дифференциального уравнения второго порядок с одном или двум сингулярным точкам. Такие задачи, как называемые двухточечные граничные задачи встречается во всех областях науки и техники. Для таких задач условия задаются в двух точках, а дифференциальные уравнения очень часто нелинейны, так что их аналитического решения обычно не существует и поэтому для получения решения нужно использовать численные методы (см. [1]).

Пусть на Г = <х: а 0 для и >0, /'(а) = 0:

Уравнение (1) определяет класс сингулярный обыкновенных дифференциальных уравнений, для которых смешанная задача. В том числе и краевой, может быть решено методом двухточечном граничном задач. Проблема исследования обыкновенных дифференциальных уравнений с сингулярной линией или точками посвящены работы [2]. В этой работе решение обыкновенных дифференциальных уравнений с сингулярной линией или точками представляется в виде аналитической функции. Полученная аналитическая формула даже для упрощенной модели удовлетворительно характеризует суть явлений. Поэтому аналитические решения задачи (1)-(2) используются как тестовые модели для первоначального анализа результатов решения распространения тепла в твердом теле при наличии источников тепла. Известно [1, стр. 9-11], что функция f (и) описывает источник тепла: она, как правило, зависит от температуры и точки константы р в зависимости от типа тела, и пластины, цилиндра или сферы принимается значения 0, 1, 2. В работе [1] для задачи (1)-(2) рассматриваются итерационные и неитерационные методов. В работе 3 изучается распространения тепла в твердом теле при независимости источников от

температуры при /(и) = Е., содержащих параметр и.

В [3] аналитическом методом построено приближенного решения задачи (1)-(2), и доказывается близости решения к граничных задач для невозмущенного

уравнения. Работа [4] посвящены асимптотическим методам, и доказывается, что решения задачи (1)-(2) совпадает с результатом работы [3].

В настоящей работе рассматриваются вопросы

численного решения задачи (1)-(2) при /Уи) = .

Следующее обстоятельство важно для практического использования предложенной схемы. Как уже было отмечено в [2], представляют интерес (и теоретический и практический) задачи, в которых (х — а) мало. В этом случае искомая функция и(ж,ц) резко меняется для малых (х — а), что, казалось бы, должно повлечь необходимость существенного измельчения сетки в этой области. Однако в предлагаемой схеме аппрок-/и йи

ведет себя и перед которым в выбранных переменных стоят операции дифференцирования без «неприятного» множителя. Это дает возможность решать задачу с очень малыми (х — а), беря практически вполне приемлемый Л.

Исследование рассматриваемого уравнения проводится примерно по тому же плану, что и исследование случая в [5]. Однако переход от оператора взятия чисто второй производной во второй слагаемой (1) к оператору с переменными коэффициентами в (1) и рассмотрение разностных схем для переменных шагов потребовали в ряде мест совершенно других методов доказательства.

2. Рассмотрим уравнение (1) дляхе J = [а, Ь] с

0 х0к (к = 1,2, •■■, N разностная схема (3)-(4)

аппроксимирует семейство задач (1)-(2) с точностью

0(И2) в класс решений С(4\а, Ь) уравнения (1) с

Теорема легко доказывается с помощью разложения по формуле Тейлора. В самом деле, пользуясь этим разложением

и(хк ± т • И) = и(хк ) + У

при т = 1, 2 и учитывая, что сумма и(хк + т • И) + и(хк — т • И) содержит только чётные

степени относительно И, получаем написанную разностную задачу (3)-(4) для (1)-(2).

Воспользовавшись трёхточечным шаблоном

(хк — И, хк, хк + И ), построим для неё разностную краевую задачу на сетке С И , то есть

= 2хк-%)+Ии ик+1 -ик 2хк-х0к)-Ии ик-ик-1 +£ ^ к=1-. ^

И 2Ихк -х0к) И Жхк -хаь) И в ‘

Пользуясь разложением функции и(х) по формуле (5), нетрудно показать (см. стр.67-69 в [6]), что погрешность аппроксимации в этом случае имеет вид

йх2 х- а йх в \ 2(хк — х0к) I йх2 \к х- а) йх

Пусть хк = а + Ик, тогда из коэффициента первого слагаемого правого части (6) следует, что

хк = + / • _, а из второго слагаемого —

х = а + и-И. Здесь хк > х0к и х > а. Отсюда видно,

Таким образом, оператор ^^ на решение и( х, /и) исходной задачи есть 0(И2), если

х0к = а + \к — / I • И.

Теперь переходим к доказательству устойчивости разностной схемы (3)-(4). С этой целью разностное уравнение (3) с условиями (4) приведём к виду

4+1 -и 2хк-и-у + Жхк) .Е =0 к=12-^-1.

h 2xt —x0t)+h/ h 2xt —x0t)+h/ 6

Разностные уравнения (7)представляют собой систему линейных алгебраических уравнений

Ви = ^, где и = (и0, , и2, —, иы ),

2И(х0 — х00) • ё — 2Кх — х01) • ё — — 2Кхм — х0М) ■ ё , 2в(х0 — х00) + И/в 2в(х- хт) + И/в ‘ 2в(хИ — хом) + Ицв)

В = <Ь..>-трёх- диагональная симметричная матрица

4x— ^ -j +1 — j k (i,ji-j*(i — 1 )2)’

h» 2h(x— xj + h2 / h j+2

Здесь s = j0 при \i— j 2|.

Матрица B положительно определена, поэтому она

имеет обратную матрицу B 1. Тогда u = — B—1 — F .

с 2( xk — x0k) — h/ Введем обозначение у = sup-k-—-—.

Решение разностную аппроксимацию задачи (3)-

(4) обладает следующими свойствами.

Лемма 1. Если у к| хк К — иЛ ^ М2.

Доказательство. Исходя из лемма 2, для этого случая несложно получить:

хк — х0к > 0 или хк — хк-1 = И > 0 . Из прин-

ципа максимума следует, что

2xk — x0k ) — hU uk — uk—1

2xk — x0k ) + hU uk — uk—1

— / ul—l\ Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

но, в случае xok > xk \uk — uk_t\ > —g. Лемма доказана.

Используя полученные оценки производных, оценивая погрешность аппроксимации в каждом узле сетки, подбирая подходящую барьерную сеточную функцию и используя метод по аналогии с [6] можно показать, что справедливо следующее:

Если u(x, u(x, /и) — решение задачи (1)-(2), uh —

решение разностной аппроксимации задачи (3)-(4), тогда найдётся постоянная M такая, что при всех k е <0,1,2, —, N>выполнится |u(xk, /) — u—| Надоели баннеры? Вы всегда можете отключить рекламу.

Разностная схема для дифференциального уравнения второго порядка

Индивидуальные онлайн уроки: Отправьте запрос сейчас: irina@bodrenko.org
Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL)
Решение задач: по математике, IT, экономике, психологии

Дифференциальные и разностные уравнения

Тема лекции: «Разностные (рекуррентные) уравнения второго порядка»

1. Линейные разностные уравнения k -го порядка.

2. Линейные разностные уравнения второго порядка с постоянными коэффициентами.

3. Модели экономической динамики с дискретным временем.

1. ЛИНЕЙНЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ k -ГО ПОРЯДКА.

1.1. Определение разностного уравнения k -го порядка.

Теория разностных уравнений находит многообразные приложения во многих областях естествознания при моделировании поведения систем различной природы. Разностные уравнения обычно возникают тогда, когда рассматриваемая величина регистрируется через некоторые (как правило, равные) промежутки времени.

Например, так называемая паутинообразная модель рынка одного товара описывается разностным уравнением вида

где P_t — цена товара в период t , a и b — некоторые числа.

Уравнение (*) представляет собой линейное разностное уравнение первого порядка с постоянными коэффициентами.

В задачах описания, анализа и синтеза дискретных динамических систем управления математические модели таких систем описываются разнообразными разностными уравнениями.

В современной теории нелинейных колебаний разностные уравнения появляются либо самостоятельно, либо при переходе от дифференциальных уравнений к точечным отображениям Пуанкаре. Такой переход в трехмерном случае значительно упрощает исследование.

В математике основным источником разностных уравнений являются дифференциальные уравнения. Имеются в виду разностные схемы, используемые для приближенного решения дифференциальных уравнений.

Многие факты теории линейных дифференциальных уравнений верны и для линейных разностных уравнений, хотя есть и некоторые различия. Отличие разностных уравнений от дифференциальных уравнений проявляется в наибольшей степени, когда уравнения нелинейны. Например, поведение решений одномерных разностных уравнений может быть таким же сложным, как и поведение решений многомерных разностных уравнений. Для динамических систем, описываемых дифференциальными уравнениями, сложное поведение имеется лишь в пространствах большой размерности ( n > 3).

Приведем простейшие примеры разностных уравнений.

Разностное уравнение второго порядка

определяет признак арифметической прогрессии. Его решением является последовательность с общим членом

где a₁ — первый член арифметической прогрессии, и d – разность арифметической прогрессии.

определяет признак геометрической прогрессии, и его решением является последовательность с общим членом

где b₁ – первый член геометрической прогрессии, q – знаменатель геометрической прогрессии.

где k − фиксированное, а n − произвольное натуральное число, y_n , y_n+1 . y_n+k – члены некоторой числовой последовательности, называется разностным уравнением k-го порядка.

Решить разностное уравнение означает найти его общее решение, т.е. все последовательности y_n = y(n) , удовлетворяющие уравнению (1).

Разностные уравнения используются в моделях экономической динамики с дискретным временем, а также для приближенного решения дифференциальных уравнений.

Между теориями разностных и дифференциальных уравнений прослеживается определенная аналогия. Если в уравнении (1) произвести формальную замену:

то определение разностного уравнения преобразуется в общее определение обыкновенного дифференциального уравнения порядка k.

Проведя формальную замену (2), нетрудно получить нормальную форму записи разностного уравнения:

Аналогичным образом определяется и задача Коши – как задача нахождения решения уравнения (3), удовлетворяющего начальным условиям:

Ниже будет показано, что решения соответствующих классов дифференциальных и разностных уравнений (например, линейных) осуществляется схожими методами.

Теорема 1. Решение y_n = y(n) задачи Коши (3), (4) при n ≥ n₀ определено однозначно.

Доказательство. Подставляя значения для y(n₀) , y(n₀+1) , . , y (n₀+ k−1) из (4) в (3), мы находим y(n₀+k) . Это, в свою очередь, дает нам возможность определить y(n₀+k+1) .

Продолжая этот процесс, можно рекуррентным способом по формуле (3) найти любое значение y(n) при n ≥ n₀ . Теорема доказана.

Следует, однако, заметить, что нахождения общего решения разностного уравнения в отличие от задачи Коши является гораздо более сложной задачей.

1. 2. Линейные разностные уравнения k -го порядка.

Определение 2. Разностное уравнение вида

где a₀ ,a₁ . a_k , f − некоторые функции от n (a₀ ≠ 0, a_k ≠ 0), называется линейным разностным уравнением k-го порядка.

Условие a₀ ≠ 0 для всех n является существенным в определении линейного разностного уравнения первого порядка. Например, линейное разностное уравнение вида

не считается уравнением первого порядка, поскольку замена к+1 = m дает уравнение

которое условно можно назвать разностным уравнением нулевого порядка.

Введем следующее обозначение:

Это выражение называется линейным разностным оператором k-го порядка .

С учетом этих обозначений уравнение (6) может быть записано в виде:

называется линейным однородным разностным уравнением, соответствующим уравнению (7). Само же уравнение (7) (при f(n) ≠ 0) называется неоднородным .

Имеют место следующие утверждения.

Теорема 2 (об общем решении линейного неоднородного уравнения).

Общее решение линейного неоднородного разностного уравнения (7) есть сумма частного решения ȳ (n) этого уравнения и общего решения y ₀( n ) соответствующего ему однородного уравнения (8).

Теорема 3 (об общем решении линейного однородного уравнения).

Пусть у (1) (n), . у (k) (n) – система, состоящая из k линейно независимых решений линейного однородного разностного уравнения (8), тогда общее решение этого уравнения задается формулой:

Множество решений линейного однородного разностного уравнения k-го порядка образует k- мерное линейное пространство, а любой набор у (1) (n), . у (k) (n) из k линейно независимых решений (называемый фундаментальным набором) является его базисом.

Признаком линейной независимости решений у (1) (n), . у (k) (n) однородного уравнения является неравенство нулю определителя Казорати:

∆ = det y n (1) ⋯ y n ( k ) ⋮ ⋱ ⋮ y n + k (1) ⋯ y n + k ( k ) 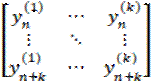, (10)

который является аналогом определителя Вронского в теории обыкновенных дифференциальных уравнений.

1.3. Линейные однородные разностные уравнения с постоянными коэффициентами k -го порядка.

В случае, когда коэффициенты a₀ , a₁ . a_k являются постоянными, методы решения линейного однородного разностного уравнения

во многом аналогичны методам решения дифференциальных уравнений с постоянными коэффициентами.

Действительно, будем искать решения уравнения в виде:

где λ ≠ 0 – некоторая постоянная. Подставляя выражение для y_n из (12) в (11), находим:

a_k λ n + k + a_{k −1} λ n + k −1 + … + a ₁ λ n +1 + a ₀ λ n = 0 .

Разделим обе части этого уравнения на λ n , получим:

Уравнение (13) называется характеристическим уравнением однородного линейного разностного уравнения.

Так же, как и в случае линейных дифференциальных уравнений с постоянными коэффициентами, знание корней характеристического уравнения, позволяет построить общее решение однородного разностного уравнения.

2. ЛИНЕЙНЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА

С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ.

Рассмотрим линейное разностное уравнение второго порядка с постоянными коэффициентами

Построим решения этого уравнения в зависимости от значения D = b 2 − 4 ac . Однако заметим, что полученные в этом случае результаты могут быть без труда перенесены на случай уравнений более высокого порядка.

В зависимости от значения дискриминанта

a λ 2 + b λ + c = 0 (15)

возможны следующие случаи.

Характеристическое уравнение (15) имеет два действительных и различных корня – λ₁ и λ₂ . Тогда λ₁ ≠ 0 и λ₂ ≠ 0 . Действительно, если хотя бы один корень равен нулю, то коэффициент приведенного квадратного уравнения (15`) c / a = λ₁ λ₂ также будет равен нулю, что противоречит определению линейного разностного уравнения второго порядка.

Корням λ₁ и λ₂ характеристического уравнения соответствуют два решения:

Покажем, что эти решения линейно независимы. Для этого вычислим определитель Казорати

∆ = det y n (1) ⋯ y n ( k ) ⋮ ⋱ ⋮ y n + k (1) ⋯ y n + k ( k )

В данном случае получим

∆ = λ 1 n λ 2 n λ 1 n +1 λ 2 n +1 = λ 1 n λ 2 n +1 — λ 2 n λ 1 n +1 = λ 1 n λ 2 n λ 2 — λ 1 .

Так как корни λ₁ и λ₂ различны, то λ₂ − λ₁ ≠ 0 , следовательно, ∆ ≠ 0 , а значит, решения линейно независимы.

В этом случае общее решение уравнения имеет вид:

где C₁ , C₂ – произвольные постоянные.

Решение примера 3.

Составим характеристическое уравнение, имеем:

Оно имеет два действительных различных корня: λ₁ = 1 , λ₂ = − 5 . Поэтому общее решение исходного уравнения в силу формулы (16) имеет вид:

Решение примера 4.

Составим характеристическое уравнение, имеем:

Оно имеет два действительных различных корня: λ₁ = 3 , λ₂ = 2 . Поэтому общее решение исходного уравнения в силу формулы (16) имеет вид:

Характеристическое уравнение имеет два комплексно сопряженных корня: λ₁ и λ₂ ,

которые, используя тригонометрическую форму записи, могут быть представлены следующим образом:

где r – модуль λ₁ , а φ – его аргумент:

Соответствующие решения разностного уравнения также комплексно сопряжены и на основании формулы Муавра имеют вид:

y (1) _n = r n (cos n φ + i sin n φ ) , y (2) _n = r n (cos n φ − i sin n φ ) .

Чтобы получить действительные решения, заменим y n ( 1 ) и y n ( 2 ) их линейными комбинациями:

Таким образом, мы получили два линейно независимых действительных решения:

z (1) _n = r n cos(n φ ) , z (2) _n = r n sin(n φ ) .

Таким образом, в данном случае общее решение имеет вид:

y(n) = r n ( C₁ cos (n φ )+ C₂ sin (n φ ) ) . (17)

Решение примера 5.

имеет два комплексно сопряженных корня –

которые могут быть записаны как:

λ ₁ = 2 (cos ( π /3) + i sin( π /3)), λ ₂ = 2 (cos ( π /3) – i sin( π /3))

Следовательно, общим решением исходного уравнения в силу формулы (17) будет:

Оба корня характеристического уравнения действительны и равны ( λ₁ = λ₂ = λ ) .

Покажем, что в этом случае кроме решения

существует еще одно решение, линейно независимое с y _n (1) .

Действительно, нетрудно убедится, что таковым является:

Сначала докажем, что y_n (2) является решением уравнения (14).

В самом деле, подставляя выражение для y_n (2) в уравнение (14) , получим:

a(n+2) λ n+2 + b(n+1) λ n+1 + cn λ n = λ n (a (n+2) λ 2 + b(n+1) λ + cn) =

= λ n (n (a λ 2 + b λ + c) + 2a λ 2 + b λ ) = 0

Последнее равенство получим в силу того, что aλ 2 + bλ + c = 0 и λ = − b /2 a .

Вычислим теперь определитель Казорати, мы имеем:

∆ = λ n n λ n λ n +1 ( n +1) λ n +1 = λ 2 n +1 ≠ 0 .

так как λ ≠ 0 . Следовательно, частные решения y_n (1) и y_n (2) линейно независимы, и общее решение уравнения (147) имеет вид:

Решение примера 6.

имеет единственный действительный корень

λ = − 3 . Следовательно, общее решение исходного уравнения таково:

Для нахождения решения неоднородного линейного разностного уравнения, так же как и в случае линейных дифференциальных уравнений, используется метод неопределенных коэффициентов, основанный на подборе частного решения неоднородного уравнения по виду правой части f(n) .

Проиллюстрируем нахождение решения неоднородного линейного разностного уравнения на примерах.

Решение примера 7.

Будем искать частное решение в виде:

Подставляя это выражение в наше уравнение (19), получим:

p (25 + 10 – 3)5 n = 64 ∙ 5 n .

Следовательно, p = 2, а значит, y*(n) = 2 ∙ 5 n .

Решая характеристическое уравнение

Общее решение однородного уравнения имеет вид:

Таким образом, общее решение неоднородного уравнения (19) имеет вид:

y( n +2) – 7y( n +1) + 10y( n ) = 4 ∙ 6 n . (20)

Решение примера 8.

Для нахождения общего решения соответствующего однородного уравнения составим характеристическое уравнение:

Для нахождения частного решения y*( n ) исходного уравнения воспользуемся методом неопределенных коэффициентов. Будем искать

Подставляя это выражение в данное уравнение (20), получим:

p6 n+2 –7 p6 n+1 + 10 p6 n = 4 ∙ 6 n .

p 6 n (36 – 42 +10) = 4 ∙ 6 n .

Следовательно, p = 1, а значит, частное решение уравнения (20) имеет вид:

Складывая общее решение соответствующего однородного уравнения и частное решение неоднородного уравнения (20), получаем общее решение уравнения:

y ( n ) = 6 n + С₁ 5 n + С₂ 2 n .

3. МОДЕЛИ ЭКОНОМИЧЕСКОЙ ДИНАМИКИ С ДИСКРЕТНЫМ ВРЕМЕНЕМ

3.1. Модель делового цикла Самуэльсона–Хикса

Рассмотрим пример, иллюстрирующий применение разностных уравнений второго порядка. Для этого мы рассмотрим модель делового цикла Самуэльсона – Хикса (динамический вариант модели Кейнса). Эта модель основывается на принципе акселерации, то есть на предположении, что объемы инвестирования прямо пропорциональны приросту национального дохода. Данное предположение характеризуется следующим уравнением:

где коэффициент V > 0 − фактор акселерации, I (t) – величина инвестиций в период t, Y (t−1) , Y (t−2) – величины национального дохода соответственно в (t−1) -м и (t−2) -м периодах.

Предполагается также, что спрос на данном этапе зависит от величины национального дохода на предыдущем этапе, то есть:

C(t) = aY(t−1) + b . (22)

Условие равенства спроса и предложения имеет вид:

Подставляя в (23) выражение для I (t) из (21) и выражение для C(t) из (22), находим:

Y(t) = (a+V)Y(t−1) − VY(t−2) + b . (24)

Уравнение (24) известно, как уравнение Хикса.

Если предположить, что на протяжении рассматриваемых периодов величины a и V постоянны, то уравнение Хикса представляет собой неоднородное линейное разностное уравнение второго порядка с постоянными коэффициентами.

Мы можем легко найти частное решение уравнения (24), если положим, что:

Y (t) = Y(t−1) = Y(t−2) = Y* , (25)

т.е. использовав в качестве частного решения равновесное решение Y* = const .

Из (24) в силу (25) имеем:

Выражение (1−a) −1 в формуле (26) носит название мультипликатора Кейнса и является одномерным аналогом матрицы полных затрат.

Рассмотреть модель Самуэльсона–Хикса при условии, что

a = 0,5 ; V = 0,5; b = 4 .

Найти общее решение уравнения Хикса.

Решение примера 9.

В этом случае уравнение (24) принимает вид:

Y(t) − Y(t−1) + 0,5 Y(t−2) = 4 .

Его частным решением (в силу формулы (26)) будет:

Y * (t) = b /(1- a ) = 4/(1 — 0,5) = 8.

Найдем корни характеристического уравнения

λ _1,2 = (1 ± i)/2 = (1/ √ 2) (cos ( π /4) ± i sin ( π /4)) .

Таким образом, общим решением соответствующего однородного уравнения является:

Следовательно, общим решением уравнения будет:

В зависимости от значений а и V возможны четыре типа динамики. Она может быть растущей или затухающей и при этом иметь или не иметь колебательный характер. Так, в рассмотренном выше примере динамика носила колебательный характер с возрастающей амплитудой.

Рассмотреть модель Самуэльсона – Хикса при условии, что

a = 0,48, V = 0,72, b = 1,3.

Найти общее решение уравнения Хикса.

Решение примера 10.

В данном случае уравнение (24) имеет вид

Y(t) – 1,2Y (t−1) + 0,72 Y(t−2) = 1,3 .

Его частным решением (в силу формулы (26)) будет:

y * (t) = b /(1- a ) = 1,3/(1 — 0,48) = 2,5.

Напишем характеристическое уравнение:

λ 2 – 1,2 λ + 0,72 = 0 .

λ_1,2 = 0,6 ± 0,6 i = 0,6 √ 2 ( cos ( π /4) ± i sin ( π /4)).

Общее решение соответствующего однородного уравнения есть

Ŷ ₀( t ) = (0,6 √ 2) t ( С₁ cos ( t π/4) + С₂ sin (t π/4) ).

Получаем общее решение данного уравнения:

В рассмотренном примере динамика носит колебательный характер с затухающей амплитудой. Очевидно, при комплексных сопряженных корнях характеристического уравнения, по модулю превышающих единицу, динамика была бы растущей. Вообще,

в зависимости от значений a и V динамика может быть растущей или затухающей и при этом иметь или не иметь колебательный характер.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

[1] Васенкова Е.К., Волкова Е.С, Шандра Е.Г. Математика для экономистов. Дифференциальные и разностные уравнения: Курс лекций. М.: Финансовая академия, 2003. 116 с.

[2] Клюшин В. Л. Высшая математика для экономистов: Учебное пособие. — М.: ИНФРА-М, 2009. — 448 с. — (Учебники РУДН).

[3] Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учебник. — 2-е изд., испр. — М.: Дело, 2001. — 688 с.

[4] Ласунский А.В. Разностные уравнения: Конспект лекций. ФГБОУ ВПО «Новгородский государственный университет им. Ярослава Мудрого», Великий Новгород, 2011.– 62с.

[5] Романко В.К . Разностные уравнения. Учебное пособие. БИНОМ. Лаборатория знаний, 2006. — 112 с.

Разностная схема для дифференциального уравнения второго порядка

4.11.2. Краевые задачи для линейного дифференциального уравнения второго порядка. Общий вид

В общем случае линейное дифференциальное уравнение второго порядка имеет вид:

Основные типы краевых условий, задаваемых на концах промежутка (изменения независимой переменной x ), на котором решается задача, имеют вид:

— условие первого рода

— условие второго рода

— условие третьего рода

На левой и правой границах промежутка могут быть заданы условия одного и того же или разного рода.

Если коэффициенты уравнения и правая часть — непрерывные функции, то краевая задача имеет единственное решение.

Дифференциальное уравнение вида (28) может быть преобразовано в уравнение в так называемой самосопряженной форме:

Для этого умножим обе части уравнения (28) на функцию . С учетом того, что

после умножения уравнение (28) можно записать в виде , т.е. в виде (29), где

4.11.3. Построение трехточечной разностной схемы 2-го порядка аппроксимации.

Рассмотрим линейное дифференциальное уравнение второго порядка в самосопряженной форме

на интервале с краевыми условиями первого рода:

Если , , то такая краевая задача описывает стационарное распределение тепла в стержне ( u(x) — температура в точке , — коэффициент теплопроводности). Задача имеет единственное решение, если — кусочно-непрерывные функции.

Введем на отрезке равномерную сетку

и запишем трехточечную разностную схему для краевой задачи (30)-(31) в прогоночном виде

где коэффициенты зависят от значений функций в узлах сетки, а также от шага .

Решение системы уравнений (32), (рассматриваемой вместе с граничными условиями) имеющей трехдиагональную матрицу коэффициентов, может быть найдено методом прогонки. Ранее этот метод описан в связи с построением кубического интерполяционного сплайна.
Формулы метода прогонки также приводятся ниже при рассмотрении вопроса о сходимости разностной схемы.

Выражения для коэффициентов разностной схемы должны обеспечивать аппроксимацию дифференциального уравнения разностной схемой с определенным порядком ее погрешности. Для получения таких выражений запишем разностную схему (32) в виде

где . Схема называется однородной, если ее коэффициенты во всех узлах сетки для любого линейного дифференциального уравнения вычисляются по одним и тем же правилам. Для однородной схемы удобна ее запись с использованием безиндексных обозначений:

Найдем погрешность аппроксимации схемы (34):

Подставляя эти выражения в (35) и группируя члены относительно функии u и ее производных, запишем погрешность аппроксимации в виде:

Условием для того, чтобы схема (34) имела второй порядок аппроксимации, будет выполнение соотношений:

Например, эти условия выполняются при

4.11.4. Сходимость разностной схемы.

Обозначим погрешность разностной схемы в узлах сетки: .

Пользуясь линейностью оператора в уравнении (34) можно установить, что погрешность в узлах сетки удовлетворяет разностной схеме:

где — погрешность аппроксимации.

Выведем оценку для погрешности в узлах сетки. Из формул (36) следует, что

поэтому схема (33) в прогоночном виде (32) запишется следующим образом:

Значения — решение схемы (39) можно найти, используя метод прогонки. Запишем соотношение

с неизвестными коэффициентами . Подставив в (39) соотношение , получим

Таким образом, для получаем рекуррентные формулы:

С учетом того, что соотношение (40) принимает вид

откуда получаем, что . Теперь можно вычислить все значения , , , по формулам (41), а затем спуститься «вниз» по i от N до 1 и найти все значения по формуле (40).

С учетом сделанного выше предположения относительно коэффициентов дифференциального уравнения (30)

, из выражения для коэффициента с следует неравенство:

, с учетом которого из неравенства (42) получаем

Тем самым из (41) следует, что .

Поскольку известно, что , то по индукции мы получаем, во-первых, решение схемы (38) в виде рекуррентных формул (40), (41) и во-вторых, справедливость неравенства

На этом основании из формулы (40) можно получить неравенство:

из которого с учетом, что , получаем неравенство: . Воспользуемся теперь рекуррентной формулой (41) для , умножив обе ее части на положительную величину :

Поскольку первый множитель справа — это коэффициент , величина которого меньше единицы, то, следовательно,

. На этом основании получаем:

с учетом, что . Наконец, поскольку , можно сделать вывод, что

Таким образом, для погрешности в узлах сетки &nbsp &nbsp можно записать неравенство

Так как , то переходя к нормам, получаем оценку погрешности решения

Такая оценка означает, что разностная схема (33) для краевой задачи (30)-(31) при указанных условиях на коэффициенты имеет второй порядок сходимости.

Прмечание. Здесь использована равномерная векторная норма

4.11.5. Краевые условия 2-го и 3-го рода.

Рассмотрим теперь уравнение (29) с краевыми условиями 2-го или 3-го рода :

Будем решать эту задачу с помощью трехточечной разностной схемы (33). Как показано в пункте 4.11.4, схема (33) имеет второй порядок аппроксимации.

Если для апроксимации условий (43) использовать простейшие односторонние двухточечные разностные производные, как в методе Эйлера, то краевые условия для разностной схемы запишутся в виде

Первое из этих условий позволяет, выражая y₀ и сравнивая это выражение с формулой вида (40) для решения y_i при i = 0, найти значения .
Второе из граничных условий вместе с формулой (40) при i = N позволяет определить значение y_N .

Однако использованные выше разностные производные имеют первый порядок погрешности аппроксимации. Чтобы краевые условия не снижали порядок аппроксции разностной схемы (33), необходимо воспользоваться односторонними разностными аппроксимациями производных, имеющими второй порядок по h.
Например, для этих целей подходит разностная производная

где, как обычно, . Действительно, по формулам Тейлора

Аналогично, разностная производная на правой границе имеет вид:

При использовании таких формул разностные аппроксимации краевых условий принимают вид:

В этом случае для разрешения трехточечной схемы (33) также может быть использован метод прогонки.
Уравнение

при i = 1 составляет с краевым условием систему

из которой можно исключить , при этом система преобразуется в уравнение

с некоторыми вполне определенными коэффициентами .

На правом конце отрезка получаем систему

из которой можно найти , а затем и все остальные (по рекуррентным формулам (40)).