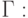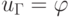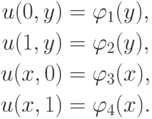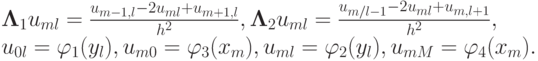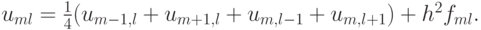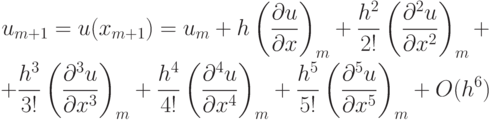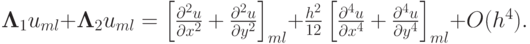Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона
Среди всех типов уравнений математической физики эллиптические уравнения с точки зрения вычислителей стоят особняком. С одной стороны, имеется хорошо развитая теория решения эллиптических уравнений и систем. Достаточно легко доказываются теоремы об устойчивости разностных схем для эллиптических уравнений. Во многих случаях получаются априорные оценки точности расчетов и числа итераций при решении возникающих систем сеточных уравнений . С другой стороны, системы сеточных уравнений , возникающие при решении уравнений методами сеток, имеют большую размерность и плохо обусловлены. Для решения таких систем разработаны специальные итерационные методы .
6.1. Постановка задачи. Простейшая разностная схема «крест». Устойчивость схемы «крест»
Будем рассматривать двухмерное уравнение Пуассона
в единичном квадрате 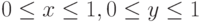
( 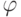
В случае прямоугольной области граничные условия удобно записать в следующем виде:
Для простоты выкладок введем равномерную расчетную сетку с узлами
Выбираем простейший пятиточечный шаблон разностной схемы «крест» . На этом шаблоне аппроксимирующее разностное уравнение легко выписать. Для этого производные заменим вторыми разностями:
где h — шаг по координатам, или в операторной форме
Эту же разностную схему можно записать в каноническом виде для разностных схем для эллиптических уравнений:
Такую каноническую запись не следует путать с канонической формой записи итерационного метода, которая встретится ниже.
Такая схема обладает вторым порядком аппроксимации по обеим координатам. Это легко показать, применяя разложение в ряд Тейлора функции — проекции точного решения на сетку — вплоть до членов четвертого порядка включительно. Проведем такое разложение для одного из операторов, стоящих в данном разностном уравнении:
Здесь учтено разложение проекции точного решения в ряд Тейлора
и аналогичное разложение для um — 1.
Для рассматриваемого двухмерного уравнения получим выражение для главного члена невязки
Рассмотрим устойчивость полученной схемы. Отметим, что методы исследования на устойчивость , применяемые для эволюционных (зависящих от времени) уравнений, здесь не работают. Действовать приходится на основе определения устойчивости.
Сформулируем и докажем две леммы, которые облегчат процедуру доказательства устойчивости разностной схемы.
Разностная схема уравнений
Разностную схему рассмотрим на примере уравнения Пуассона в прямоугольнике, используя для аппроксимации второй производной конечные разности второго порядка точности (7.1.4). Вводя сетку 



или , введя обозначение 
Данная неявная схема охватывает все внутренние точки области 

 |
Пусть для простоты 
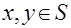











Здесь 

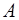
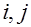
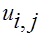





Пятидиагональная матрица 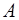
Вектор правой части СЛАУ 

где 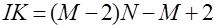

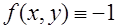

На рис.3 показано распределение функции решения аналогичной краевой задачи в двумерной области при порядке СЛАУ 





Отметим, что матрица задачи при 

Лабораторные задания к теме «Численное решение уравнений в частных производных»
Лабораторные работы по теме могут быть выполнены с помощью математических пакетов программ Mathcad или Matlab. В результате работы должна быть представлена искомая сеточная функция в виде матрицы значений в узлах сетки либо в виде послойного по времени распределения значений сеточных векторов. Следует также привести графическое представление результатов.
Гиперболические уравнения
Варианты заданий для одномерного волнового уравнения с граничными и начальными условиями (см. 7.2).
| № п/п |  |  |  |  | 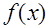 |  |  |  | Метод  |
| 1.1 |  |  | 0.1, 0.05 | ||||||
| 1.2 |  |  | 0.1, 0.05 | ||||||
| 1.3 | 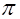 |  |  | 0.1, 0.05 | |||||
| 1.4 |  |  | 0.1, 0.05 | ||||||
| 1.5 | 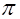 |  |  | 0.1, 0.05 | |||||
| 1.6 |  |  | 0.1, 0.05 | ||||||
| 1.7 | 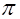 |  |  | 0.1, 0.05 | |||||
| 1.8 | 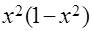 |  | 0.1, 0.05 | ||||||
| 1.9 | 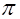 |  |  | 0.1, 0.05 | |||||
| 1.10 |  |  | 0.1, 0.05 |
Параболические уравнения
Варианты заданий для одномерного уравнения теплопроводности с граничными и начальными условиями (см. 7.3).
| № п/п |  |  |  |  | 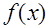 |  |  |  | Метод  |
| 2.1 | 0.1 |  |  | 0.01 | |||||
| 2.2 |  |  | 0.01 | ||||||
| 2.3 | 0.1 |  |  | 0.01 | |||||
| 2.4 |  |  | 0.01 | ||||||
 2.5 2.5 |  | 0.1 |  |  | 0.01  | ||||
| 2.6 |  |  |  | 0.01  | |||||
| 2.7 | 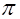 | 0.1 |  |  | 0.01 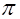 | ||||
| 2.8 | 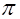 |  |  | 0.01 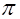 | |||||
| 2.9 | 0.1 |  |  | 0.01 | |||||
| 2.10 |  |  | 0.01 | ||||||
| 2.11 | 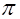 | 0.1 |  |  | 0.01 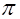 | ||||
| 2.12 | 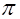 |  |  | 0.01 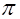 |


Эллиптические уравнения
Решить заданную краевую задачу методом сеток, сведением её к СЛАУ и последующим решением прямым (стандартным) и итерационным (Зейделя-ОСП) методами. Сравнить с существующим строгим решением.
Варианты заданий для краевой задачи с уравнениями эллиптического типа (см. 7.4).
| № п/п | Уравнение  |  |  |  | 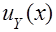 |  |  |  |  |
| 3.1 |  | 0.2, 0.1 | — | ||||||
| 3.2 |  |  |  | 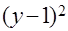 | 0.2, 0.1 | -1 | |||
| 3.3 |  | 0.2, 0.1 | — | ||||||
| 3.4 |  | 0.2, 0.1 | 0, 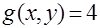 | ||||||
| 3.5 | 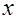 |  | 0.2, 0.1 | — | |||||
| 3.6 |  |  |  | 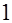 | 0.2, 0.1 |  | |||
| 3.7 | 0.5, 0.25 | — | |||||||
| 3.8 |  | 0.2, 0.1 | — 2 | ||||||
| 3.9 | 0.25,0.1 | — | |||||||
| 3. |  |  |  |  | 0.2, 0.1 |

Литература
1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Лаборатория Базовых Знаний, 2001. – 632с.
2. Мэтьюз Д.Г., Финк К.Д., Численные методы. Использование MATLAB, 3-е издание,: Пер. с англ. – М.: Изд. «Вильямс», 2001. – 720 с.
3. А.Б.Самохин, А.С.Самохина. Численные методы и программирование на Фортране для персонального компьютера.- М.: Радио и связь, 1996. – 224 с.
4. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1970. – 644с.
5. Вержбицкий В.М., Численные методы (Математический анализ и обыкновенные дифференциальные уравнения) – М.: Высшая школа, 2001.– 382с.
6. Заварыкин В.М., Житомирский В.Г., Лапчин М.П. Численные методы. – М.: Просвещение , 1991. – 176с.
Содержание
1. Абсолютная и относительная погрешности. 3
1.1. Число верных знаков приближенного числа. 4
1.2. Погрешность функций. 5
1.3. Погрешность простейших функций двух переменных. 5
1.4. Примеры и задания. 6
2. Приближение функций. 10
2.2. Интерполяционный полином Лагранжа. 11
2.3. Интерполяционный полином Ньютона. 12
2.3. Примеры и задания для практических занятий. 15
3. Численные методы решений трансцендентных и алгебраических уравнений 18
3.1. Метод простой итерации для решения нелинейных и трансцендентных уравнений. 19
3.2. Метод хорд и секущих. 20
3.3. Метод касательных. 21
3.4. Скорость сходимости итерационных методов. 22
3.5. Пример и задание для практических занятий. 24
4. Численное интегрирование. 25
4.1. Метод Ньютона – Котеса. 25
4.2. Метод прямоугольников. 26
4.3. Метод трапеций. 27
4.4. Метод парабол. (Метод Симпсона) 28
4.5. Квадратурные формулы Гаусса. 29
4.6. Задание для практических занятий. 31
5. Численные методы линейной алгебры.. 32
5.1. Численное решение СЛАУ.. 32
5.2. Прямые методы решения СЛАУ.. 35
5.2.1. Метод Гаусса (Метод исключений) 36
5.2.2. Вычислительная схема метода Гаусса. 37
5.2.3. Ортогонализация матриц. 39
5.2.4. Решение системы уравнений методом ортогонализации. 40
5.3. Итерационные методы решения СЛАУ.. 41
5.3.1. Метод простой итерации. 41
5.3.2. Метод Якоби и метод Зейделя. 43
5.3.3. Метод оптимального спектрального параметра (ОСП) для простой итерации. 46
5.4. Нахождение собственных векторов и собственных значений матриц 52
5.5. Примеры и задания к теме. 53
5.5.1. Прямые методы решения СЛАУ.. 53
5.5.2. Итерационные методы решения СЛАУ.. 57
5.5.3. Нахождение собственных значений и векторов. 61
6. Численные методы решения обыкновенных дифференциальных уравнений 62
6.1. Метод разложения в ряд Тейлора. 63
6.2. Общая схема метода Рунге — Кутта. 63
6.3 Методы Рунге-Кутта низших порядков. 64
6.3.1 Метод Эйлера. 64
6.3.2. Метод трапеций и прямоугольника. 65
6.4. Методы Рунге-Кутта высших порядков. 65
6.5. Задание к теме и пример решения ОДУ.. 67
7. Численное решение начально-краевых задач для дифференциальных уравнений в частных производных. 68
7.1. Конечные разности. 69
7.2. Гиперболическиеуравнения. 70
7.3. Параболическиеуравнения. 72
7.4. Уравнения эллиптическоготипа. 75
7.4.1. Разностная схема уравнений. 75
7.5. Лабораторные задания к теме «Численное решение уравнений в частных производных». 79
20. Метод установления решения задачи Дирихле для уравнения Пуассона. Схема переменных направлений
- Ростислав Водосвятский 5 лет назад Просмотров:
1 Варианты заданий 0. Метод установления решения задачи Дирихле для уравнения Пуассона. Схема переменных направлений 0.1. Постановка задачи Рассматривается задача Дирихле для эллиптического уравнения Lu = f(x, ), (x, ) G, (1) u = µ(x, ), (x, ) Γ. () Пусть G = G + Γ = <0 x l x, 0 l >прямоугольник, а Lu = ( p (x, ) u ) + ( q(x, ) u ), (3) x x p (x, ), q(x, ) достаточно гладкие функции, 0 2 так что Lu = L 1 u + L u. Операторы L 1 и L заменим разностными операторами Λ 1 и Λ Здесь Λ 1 u = p i+ 1 j u i+1j u h x u +1 u Λ u = q + 1 h q 1 u u i 1j p i 1 j, (5) h x u u 1 h. (6) Обозначим p i+ 1 j = p(x i + h x /, j ), p i 1 j = p(x i h x /, j ), q + 1 = q(x i, j + h /), q 1 = q(x i, j h /). Λu = Λ 1 u + Λ u, 1 i N x 1, 1 j N 1. Если u(x, ) имеет не менее четырех непрерывных ограниченных в рассматриваемой области G производных по x и по, а p(x, ) и q(x, ) не менее трех, то разностный оператор Λ аппроксимирует дифференциальный L со вторым порядком, т. е. Lu Λu = O( h ), h = h x + h. Итак, решение задачи (1)-() свелось к решению разностной задачи Дирихле (Λ 1 u + Λ u ) = f, 1 i N x 1, 1 j N 1 (7) при граничных условиях u i0 = µ(x i, 0), 0 i N x, u in = µ(x i, l ), 0 i N x, u 0j = µ(0, j ), 0 j N 1, u Nxj = µ(l x, j ), 0 j N 1. (8) 0.3. Метод установления решения задачи Дирихле для уравнения Пуассона Для вычисления решений многих стационарных задач математической физики, описывающих равновесные состояния, рассматриваются последние как результат установления развивающегося во времени процесса, расчет которого оказывается проще, чем прямой расчет равновесного состояния. Рассмотрим вспомогательную нестационарную задачу о распространении тепла u = L 1 u + L u + f(x, ), t (9) u Γ = µ(x, ), u(x,, 0) = u 0 (x, ), где f(x, ) имеет прежний смысл, а u 0 (x, ) произвольно. Поскольку источники тепла f(x, ) и температура на границе µ(x, ) не зависят от времени, то естественно ожидать, что и решение u(x,, t) с течением времени будет меняться все медленнее, распределение температур в пределе при t превратится в равновесное распределение температуры u(x, ), описываемое исходной задачей (1)-(). Надо решать задачу до тех пор, пока ее решение не перестанет меняться в пределах интересующей нас точности. Рассмотрим вначале разностную схему, с помощью которой могла бы решаться задача (7)-(8), но на практике ее не применяют по указанным в п. 0. причинам. 0.. Двухслойная схема с весами Аппроксимируем задачу (9) разностной схемой u k τ = Λ(σ + (1 σ)u k ) + f(x i, j ), 1 (10) 1 При решении стационарных задач методом установления k номер итерации, а τ итерационный параметр, который выбирается из соображений точности аппроксимации и быстроты сходимости.
3 i = 1. N x 1, j = 1. N 1, k = 0, 1. i0 = µ(x i, 0), 0 i N x, in = µ(x i, l ), 0 i N x, 0j = µ(0, j ), 1 j N 1, N xj = µ(l x, j ), 1 j N 1. Решение при k = 0 находится из начального условия в (9) (11) Рассмотрим два варианта значений параметра σ. u 0 = u 0 (x i, j ), i = 0, 1. N x, j = 0, 1. N. а) При σ = 0 получаем явную схему и решение во внутренних узлах сетки вычисляется по формуле = u k + τ(λ 1 u k + Λ u k ) + τf(x i, j ), (1) i = 1. N x 1, j = 1. N 1, k = 0, 1. Схема (1) условно устойчива при τ Ah. Общее число действий при переходе со слоя на слой пропорционально числу узлов сетки, т. е. O(N x N ) схема экономичная. б) При σ = 1 получаем неявную схему. Она устойчива при любых h и τ. Для определения на каждом слое линейную систему получаем τ(λ 1 + Λ ) = u k + τf(x i, j ), (13) i = 1. N x 1, j = 1. N 1, k = 0, 1. Матрица этой системы пятидиагональная и решать систему можно методом матричной прогонки или методом исключения Гаусса, который при учете специального вида матрицы требует O(N xn ) действий, т. е. схема не является экономичной Схема переменных направлений Эта схема сочетает лучшие качества явной схемы экономичность и неявной устойчивость. Наряду с основными значениями u k и uk+1 вводится промежуточное значение /, которое формально можно рассматривать как значение при t = t k+ 1 = t k + τ. Решение задачи в этом случае сводится к решению двух систем вида (1)-(15) с трехдиагональными матрицами. u k+ 1 u k τ/ = Λ 1 u k+ 1 + Λ u k + f(x i, j ), (1) 1 i N x 1, 1 j N 1. 3
4 u k+ 1 τ/ = Λ 1 u k+ 1 + Λ + f(x i, j ), (15) 1 i N x 1, 1 j N 1. k = 0, 1. В граничных узлах решение должно принимать заданные в (11) значения. Схема (1) неявна по направлению x и явна по направлению, а схема (15) явна по направлению x и неявна по направлению, что позволяет использовать для нахождения решения одномерные прогонки. Система (1) с учетом граничных условий (11) может быть записана в следующем виде: u k+ 1 0j = µ(0, j ), где A u k+ 1 i 1j B u k+ 1 + C u k+ 1 i+1j = G k+ 1, 1 i N x 1, u k+ 1 N xj = µ(l x, j ) (16) G k+ 1 = u k τ (Λ u k + f(x i, j )), (17) 1 j N 1. В итоге при каждом 1 j N 1 получили линейную замкнутую систему (N x + 1)-го порядка относительно u k+ 1 0j, u k+ 1 1j. u k+ 1 N xj. Матрица системы 3-х диагональная и решать систему следует методом прогонки. Прогонки осуществляются вдоль строк (рис. ). u k u k+ 1 l Рис. l x x При j = 0, j = N решения находятся из (11): u k+ 1 i0 = µ(x i, 0, t k+ 1 ), 0 i N x, u k+ 1 in = µ(x i, l, t k+ 1 ), 0 i N x. Система (15) с учетом граничных условий (11) может быть записана в следующем виде: i0 = µ(x i, 0), A 1 B + C +1 = G k+1, 1 j N 1, in = µ(x i, l ), где (18) (19) G k+1 = u k+ 1 τ (Λ 1u k+ 1 + f(x i, j )), (0) 1 i N x 1,
http://megalektsii.ru/s30349t4.html
http://docplayer.com/40127205-20-metod-ustanovleniya-resheniya-zadachi-dirihle-dlya-uravneniya-puassona-shema-peremennyh-napravleniy.html