Разностное уравнение фильтра скользящего среднего

Разностное уравнение фильтра скользящего среднего

Алгоритмическое обеспечение (Лекция)

1. Алгоритмы первичной обработки информации

2. Алгоритмы вторичной обработки информации

3. Алгоритмы прогнозирования значений величин и показателей

4. Алгоритмы контроля

Алгоритмическое обеспечение – совокупность взаимосвязанных алгоритмов. Множество алгоритмов делятся на 6 групп:

1) Алгоритмы первичной обработки информации (фильтрация, учет нелинейности характеристики).

2) Алгоритмы определения показателей процесса (алгоритмы вторичной обработки информации), определение интегральных и средних значений, скорости, прогнозирования и т.д.

3) Алгоритмы контроля.

4) Алгоритмы цифрового регулирования и оптимального управления.

5) Алгоритмы логического управления.

6) Алгоритмы расчета технико-экономических показателей.

1. Алгоритмы первичной обработки информации

Первичная обработка информации включает фильтрацию полезного сигнала, проверку информации на достоверность, аналитическую градуировку датчиков, экстраполяцию и интерполяцию, учет динамических связей.

Фильтрация – операция выделения полезного сигнала измерительной информации из его суммы с помехой. В зависимости от помех выделяют следующие фильтры:

1. фильтры низких частот (НЧФ).

2. высоко — частотные фильтры (ВЧФ).

3. полосовые фильтры (ПФ, пропускают сигналы определённой частоты).

4. режекторные фильтры (ПФ, не пропускают сигналы определенной частоты).

Наиболее распространенными являются НЧФ, которые подразделяются на фильтры скользящего среднего, фильтры экспоненциального сглаживания и медианные.

Разностное уравнение фильтра экспоненциального сглаживания

Получим уравнение фильтра экспоненциального сглаживания при следующих допущениях:

допущение 1: полезный сигнал x ( t ) представляет собой случайный стационарный процесс с известными статическими характеристиками M_x – математическое ожидание; D_x – дисперсия; — автокорреляционная функция, показывающая степень связи между значениями сигнала в моменты времени, сдвинутые относительно друг друга на время τ. Полезный сигнал не коррелирован с помехой.

допущение 2: помеха f ( t ) представляет собой случайный стационарный процесс, некоррелированный с полезным сигналом и с известными статическими характеристиками M_f =0; ; при этом k m >0.

В непрерывном варианте свойства фильтра экспоненциального сглаживания описываются ДУ:

.

Передаточная функция — апериодическое звено

.

Заменив производную — разностью и получаем разностное уравнение:

– разностное уравнение

, а ,

где Т – постоянная времени;

Т ₀ – период опроса датчика;

γ – параметр настройки регулятора.

Оптимальное значение γ определяется путём минимизации погрешности фильтра. Оптимальное значение параметра настройки фильтра зависит от статических свойств полезного сигнала, помехи. На практике в большинстве случаев эти параметры определить нельзя, чем меньше γ, тем сильнее сглаживающее свойство фильтра, однако при малых значениях γ может произойти искажение полезного сигнала.

Данный фильтр является самым распространенным низкочастотный фильтром.

Разностное уравнение фильтра скользящего среднего

В аналоговом виде (непрерывный вариант) уравнение ФСК имеет вид:

.

Используя метод прямоугольников можно получить разностное уравнение:

Заменив интеграл суммой (применяя для интегрирования метод прямоугольников), получим:

где — площадь прямоугольников;

Т – время усреднения;

Т= nT ₀ , n – это число точек усреднения, параметр настроек фильтра. Оптимальное значение n определяется путём минимизации погрешности (дисперсии ошибки) фильтра и зависит от статических свойств полезного сигнала и помехи.

Чем больше n , тем больше сглаживающее свойство фильтра.

Статические фильтры нулевого порядка

Статический фильтр – фильтр, который в аналоговом варианте представляет собой параллельное соединение ( n +1) цепочек, состоящих из усилительного звена и звена чистого запаздывания.

ПФ такого фильтра имеет вид:

где τ – время запаздывания;

n – порядок фильтра;

При n =0 имеем статический фильтр нулевого порядка W ( p )= b _{0 →} .

При использовании данной формулы y ( t ) будет смещённой оценкой полезного сигнала x ( t ),

т.е. — математическое ожидание выходного сигнала.

Для получения несмещённой оценки необходимо использовать следующую функцию:

.

В этом случае .

b ₀ в качестве параметра настройки .

Для программной реализации статического фильтра нулевого порядка используют формулу:

.

Статические фильтры первого порядка

ПФ таких фильтров имеет вид:

.

Математическое ожидание:

Для того чтобы фильтр имел несмещенную оценку при учете

, где — параметры настройки фильтра.

Минимизируя значение ошибки фильтрации, получаем: .

Для программной реализации — — период опроса датчика.

Разностное уравнение: .

при n =0 имеем статический фильтр нулевого порядка W ( p )= b ₀ .

При использовании данной формулы y ( t ) будет смещённой оценкой полезного сигнала x ( t ), т.е. — математическое ожидание выходного сигнала

Для получения несмещённой оценки необходимо использовать следующую функцию:

.

В этом случае .

b ₀ в качестве параметра настройки .

Для программной реализации статического фильтра первого порядка используют формулу: .

Фильтры данного типа предназначены для фильтрации аномальных выбросов. К числу робастных фильтров относят медианный фильтр, фильтр релейно-экспоненциального сглаживания.

Реализация медианного фильтра осуществляется по формуле: ,

где М – параметр настройки; med – оператор, означающий операцию оценки медианы.

Оценка медианы проводится по следующему алгоритму:

Проводится упорядочение отсчетов в ряд по возрастанию.

При нечетном М в качестве медианы выбирается центральное значение этого ряда. При четном значении в качестве медианы выбирается полусумма двух средних значений ряда.

Фильтр релейно-экспоненциального сглаживания

Алгоритм работы данного фильтра имеет вид:

,

где σ — среднеквадратическое отклонение (СКО) помехи;

Δ — модуль приращения полезного сигнала на соседних отсчетах.

Разностные уравнения фильтров с заданной АЧХ

Если необходимо реализовать низкочастотный фильтр с заданной АЧХ, то для этих целей необходимо использовать ЛАЧХ (логарифмическая АЧХ).

— зависимость коэффициента передачи гармонического сигнала от частоты.

.

Необходимо определить ЛАЧХ, а затем ПФ и далее от ПФ перейти к дискретной ПФ, используя преобразования Лапласа.

Передаточная функция (ПФ) – отношение, в изображении Лапласа выходной функции к входной при нулевых начальных условиях.

, ;

, где р – комплексная величина.

.

Произвели замену переменной:

.

Переход от ПФ к дискретной ПФ может быть произведен на основе от ношения: .

После получения дискретной ПФ можно легко получить разностное уравнение, пользуясь теоремой о смещении (запаздывании):

— смещенная решетчатая функция

.

Не рекуррентная, не рекурсивная система: — наличие только входных сигналов в правой части, — наличие выходных сигналов.

Для АЧХ, вида

(*);

.

A и B подставляем в выражение (*) и ДПФ определена. Далее необходимо написать разностное уравнение и составить программу.

Теорема о смещении:

;

.

Преобразуем, применяя теорему о смещении, и получаем

.

Для высокочастотного фильтра с характеристикой : ;

;

.

Для полосового фильтра:

;

;

.

Для режекторного фильтра:

;

;

.

Для реализации процедуры фильтрации применяются и другие фильтры кроме рассмотренных, являющиеся более сложными адаптивными и АЧХ с крутыми фронтами. К числу таких фильтров относят фильтры Чебышева, Калмана, Винера.

Проверка достоверности информации

Недостоверность информации появляется при отказах информационно-измерительных каналов. Отказы бывают двух видов: полные и частичные. Полный отказ наступает при выходе из строя измерительного преобразователя, или при повреждении линии связи. При частичном отказе технические средства сохраняют работоспособность, однако погрешность измерения превышает допустимое значение.

Алгоритмы, позволяющие обнаруживать полные отказы:

1) алгоритм допускового контроля параметра : проверка условия — X_i min ≤ X_i ≤ X_i max

X_i min – минимально возможное значение i -го параметра;

X_i max – максимально возможное значение i -го параметра.

Если условие не выполняется, то информация недостоверная. В этом случае используют достоверную информацию, полученную в предшествующий момент времени, либо используют среднее значение i -го параметра.

2) А лгоритм основан на определении скорости изменения i -го параметра и проверки условия :

dX_i ( t )/ dt =( X_i ( k )- X_i ( k -1))/ T ₀ , где T – период опроса, T=dt

3) Алгоритм аппаратного резервирования – алгоритм контроля информации, с помощью которого выявляются частичные отказы, основанные на использовании информационной избыточности. Избыточность может быть получена путем резервирования информационно – измерительных каналов (аппаратная избыточность), или путем определения некоторых параметров с помощью прямого измерения, так и путем расчетов через другие параметры.

Аппаратная избыточность – признак отказа, нарушение условия — | X_i — ­ X ­| C , где

‌Х­ – это среднее значение по всем измерительным преобразованием

X_i – значение, полученное от i измерительного преобразования

С – наибольшее допустимое значение модуля разности (2-3 от средне квадратичной погрешности изменения преобразования)

4) Уравнение материального баланса имеет вид: f ( x ₁ , x ₂ , …. x_n )=0. Уравнение выполняется лишь в том случае, если значения параметров x ₁ , x ₂ , …. x_n соответствуют истинным значениям. Если параметры изменяются с погрешностью , имеем . При подстановке значений , получим . Если , то информация считается недостоверной.

Алгоритмы аналитической градуировки датчиков

X — измеряемая величина; Y — установившийся сигнал

Статическая характеристика датчика y = f ( x ).

Под аналитической градуировкой датчика (АГД) понимают определение (восстановление) измеряемой величины по сигналу, снимаемому с датчика (преобразователя).

, где — оценка измеряемой величины, полученная по сигналу, снимаемому с датчика; f -1 – обратная функция y = f ( x ).

Если градуировочная характеристика измерительного преобразования задана аналитически, то АГД сводится к реализации вычислительной операции.

Если статическая характеристика датчика линейная: y = ax + b , то аналитическая градуировка сводится к реализации вычислительных операций, то есть к формуле =( y — b )/ a .

В этом случае аналитическая градуировка датчика выражается в масштабировании. Однако большинство промышленных датчиков (преобразователей) имеют нелинейную статическую характеристику, которая часто определяется экспериментально и представляется в виде графика или градуировочной таблицы (для этого используют паспортные данные). При табличном представлении градуировочной характеристики применяют способ АГД, заключающийся в аппроксимации градуировочной характеристики аналитическим выражением. Одним их наиболее распространенных методов аналитической градуировки является аппроксимация при помощи степенных полиномов:

где — коэффициенты, которые должны быть численно определены;

n – степень полинома.

Используя эту формулу, возникает ряд задач:

1. Выбор критерия, по которому определяется коэффициенты a_j ;

2. Определение степени полиномов ( n ), обеспечивающие требуемую точность аппроксимации.

В зависимости от критерия, используемого для аппроксимации, различают следующие полиномы:

1. Полиномы наилучшего равномерного приближения (НРП).

Критерием определения коэффициентов данных полиномов выступает требование обеспечения заданной точности в любой точке диапазона работы датчика. Для аппроксимации данного полинома необходимо минимизировать линейную форму, для чего используются методы линейного программирования (решение задачи оптимизации). Линейное программирование – раздел математики, в которых рассматриваются методы определения экстремума линейного критерия при линейных ограничениях. Наиболее распространенный метод линейного программирования – симплекс метод (метод последовательно улучшения плана). Недостатком полинома НРП является сложность определения коэффициентов, то есть необходимость решения задачи линейного программирования.

2. Асимптотические полиномы.

Достоинством является возможность предварительной оценки степени полинома до расчёта коэффициента. Расчёт коэффициентов базируется на градуируемой таблице. Приведем фрагмент этой таблицы:

x ₀ , x ₁ , x ₂ – значения измеряемого параметра, соответствующие y ₀ , y ₁ , y ₂

3. Регрессионные полиномы используются для АГД нестандартных датчиков. В качестве критерия определения коэффициентов принимается величина среднеквадратической погрешности аппроксимации в диапазоне изменения измеряемой величины: (минимизируется сумма квадратов ошибок)

Для определения коэффициентов полинома используется метод наименьших квадратов, при котором минимизируется критерий и решается система уравнений:

Сравнивая разные полиномы можно сделать вывод: регрессионные полиномы дают наименьшую среднеквадратичную ошибку. Полиномы НРП дают минимум максимальной ошибки, а асимптотические занимают промежуточное положение между ними.

Применение интерполяции и экстраполяции при контроле параметров и показателей

Процесс получения инфо о непрерывно-изменяющихся величинах в АСУ ТП происходит дискретно во времени, поэтому возникает задача восстановления значений измеряемых величин в моменты времени, несовпадающие с моментами замеров.

Для управления, когда необходимо знать значение измеряемой величины в текущий или будущий момент времени используется метод экстраполяции значения величины, полученной в предшествующий момент времени.

Для анализа работы производства и вычисления технико-экономических показателей необходимо определить значение величин в предшествующие моменты времени, в этом случае используются методы интерполяции.

В большинстве случаев экстраполяцию осуществляют ступенчатым методом. При ступенчатой экстраполяции о значении измеряемой величины в любой текущий момент времени судят по измеренному значению величины последней токи замера. Погрешность ступенчатой экстраполяции:

,

где — автокорреляционная функция (устанавливает степень связи);

T ₀ — период опроса датчик а;

— погрешность измерительного преобразования.

Таким образом, погрешность ступенчатой экстраполяции зависит от статических свойств измеряемой величины, периода опроса и погрешности измерительного канала, что необходимо учитывать при выборе периода опроса.

Для интерполяции чаще всего применяется кусочно-линейная аппроксимация, которая проводится по двум точкам с использованием следующей формулы:

Менее точной является ступенчатая интерполяция.

Учёт динамический связей

Наличие инерционного датчика может существенно исказить частотный состав измеряемого сигнала, например, при измерении температуры в печах применяют массивные чехлы для защиты термопар от механических повреждений, что вызывает значительную динамическую погрешность.

Если принять статический коэффициент передачи инерционного датчика равный единице, то есть при , то необходимо учитывать следующую связь: , т.е. в текущий момент времени на выходе датчика формируется сигнал несущий информацию о значении параметра в предшествующий момент времени, т.е. в момент времени .

2. Алгоритмы вторичной обработки информации

К основным операциям вторичной обработки относят:

1) определение интегральных и средних значений величин и показателей;

2) определение скорости изменения величины и показателей;

3) определение величин и показателей, неизмеряемых прямым методом (косвенное измерение);

4) прогнозирование значений величин;

5) определение статических характеристик, величин и показателей.

Применяются для управления и анализа работы. Большое значение имеет определение суммарных количеств вещества или энергии, получаемых в производстве за определенный интервал времени. Примерами являются расходы электроэнергии, топлива за час, смену, сутки и так далее. Этим же целям служит определение средних значений измеряемых величин, являющихся режимными показателями (среднее время, среднее давление и т.д.)

Рассмотрим методы дискретного интегрирования, непрерывно изменяющейся во времени измеряемой величины. Далее приведены численные методы интегрирования.

1. Метод прямоугольников.

Суть метода состоит в замене реализации x( t ) её ступенчатой экстраполяцией за время t .

, , где — период опроса датчика.

В представленном виде алгоритм интегрирования используется редко, для его реализации требуется запоминать все значения . На практике используется рекуррентная формула:

, .

2. Метод трапеций.

Более точным является метод трапеции. Рекуррентная формула: .

Погрешность метода трапеции меньше погрешности метода прямоугольников на величину:

.

Как показывают расчеты приблизительно на 10% уменьшается погрешность дискретного интегрирования при переходе от метода прямоугольника к методу трапеции при n >10, когда существеннее влияние на результат расчета оказывают кратные числа, следовательно, на практике в большинстве случаев используют метод прямоугольников, как более простой и экономичный.

Среднее значение определяется через интегральное:

,

где — время интегрирования.

Дифференцирование дискретно – измеряемых величин. Для анализа хода технологического процесса весьма важным является определение не только численных значений параметров, но и тенденция их применения в текущий момент времени (увеличивается параметр или уменьшается). В этом случаи необходимо определять скорость изменения параметра, то есть осуществлять дифференцирование.

Производная от ошибки необходимо определять и при реализации регулятора, например с ПД, ПИД звеньями.

Наиболее простой алгоритм дискретного дифференцирования основан на использовании следующей функции: , где Т₀ – период опроса датчика.

3. Алгоритмы прогнозирования значений величин и показателей

Для расчета прогнозируемых значения необходимо построить математическую модель временного ряда. В практике краткосрочного прогнозирования наибольшее распространение получили модель авторегрессии и полиномиальная модель.

Модель авторегрессии имеет вид: , где а – коэффициенты, р – порядок. Расчет прогнозируемых значений проводится по формуле: , где — измеренные или прогнозируемые значения временного ряда в моменты времени t =( n — k + l ) To .

Данный алгоритм прост в реализации, но его недостатком является низкая точность, так как результаты а(к) не уточняются по результатам прогноза. Этого недостатка лишен метод полиномиальной модели: , где n — номер текущего шага, l — число шагов прогноза.

Оценка параметров этой модели а уточняется по мере поступления каждого нового значения временного ряда. Для этих целей используется экспоненциальные средние различного порядка.

1 порядка: Z ₁ ( j )=γ y ( j )+(1-γ) Z ₁ ( j -1)

2 порядка: Z ₂ ( j )=γ Z ₁ ( j )+(1-γ) Z ₂ ( j -2)

r порядка : Z_N ( j )=γ Z_{r -1} ( j )+(1-γ) Z_r ( j -1), где — параметр настройки прогнозирования.

Выбор данного параметра основывается на следующих свойствах: если желательно чтобы прогноз базировался на последних значениях временного ряда, то следует выбирать значение , близкое к 1. Если необходимо учитывать и предыдущие значения временного ряда, то необходимо уменьшать.

Расчет коэффициентов осуществляется по формуле для модели 1 порядка:

Расчет коэффициентов осуществляется по формуле для модели 2 порядка:

Коэффициенты в полиномиальном законе рассчитываются через модели 1 и 2 порядка; модели высшего порядка применяются редко, т.к. качество прогноза растет незначительно.

Определение статистических показателей измеряемых величин

Знание статистических характеристик необходимо для оценки качества выпускаемой продукции и определения момента нарушения хода ТП. В этом случае меняются значения статистических характеристик измеряемых величин. Особенностью определения lfyys [ характеристик является использование рекуррентных формул.

Математическое ожидание (1 – не рекуррентная формула, 2 – рекуррентная формула)

Дисперсия (1 – не рекуррентная формула, 2 – рекуррентная формула)

4. Алгоритмы контроля

Понятие контроль более широкое понятие и включает в себя измерение величин и показателей и сравнение их с допустимыми пределами.

Рассмотрим общие и частные постановки задачи определения величин и показателей.

Задана совокупность величин и показателей, которые необходимо определить в объекте контроля. Указана требуемая точность их оценки. Имеется совокупность датчиков, которые установлены или могут быть установлены на автоматизированном объекте. Требуется для каждого отдельного показателя найти группу датчиков, частоту их опроса и алгоритмы обработки, получаемых от них сигналов. В результате чего значение этой величины определилось бы с требуемой точностью.

Точность оценки искомой величины определяется точностью работы измерительных цепей (датчика, преобразователя), частотой их опроса и точностью вычислительной переработки измерительных сигналов в искомую величину.

1. Определение текущего значения величины непосредственно измерением автоматическим прибором или датчиком.

— когда требуемая точность измерения намного меньше точности датчика с преобразователя;

— когда требуемая точность измерения больше точности датчика или преобразователя.

Второй случай является более общим. Для контроля необходимо найти такие алгоритмы преобразования сигнала датчика, которые бы увеличили точность до требуемого значения. Для этого необходимо произвести анализ существующей погрешности и выявить отдельные ее составляющие, а затем их скомпенсировать, путем использования специальных алгоритмов.

В зависимости от причин возникновения погрешностей применяют следующие алгоритмы, уменьшающие погрешность:

Аналитическая градуировка датчиков.

Если погрешность вызвана нелинейностью статической характеристики датчика.

Фильтрация сигнала от помех.

Если внутри объекта или датчика существует источник значительной помехи, который накладывается на полезный сигнал.

Экстраполяция и интерполяция

Если значительная погрешность оценки величины вызвана большим значением периода опроса.

Коррекция динамической погрешности датчика

Если датчик представляет собой инерционное звено, а измеряемая величина меняется во времени со значительной скоростью.

2. Определение значения величины, вычисляемой по измеренным датчиком сигналам.

Например, оценка суммарного значения, среднего значения, скорости и т. д. В этом случае необходимо выбрать рациональные алгоритмы переработки измеряемого сигнала.

Кроме того здесь не исключено применение алгоритмов АГД, фильтрации и т. д.

Данная задача наиболее сложна в тех случаях, когда не известен характер связи между измеряемыми сигналами и искомой величиной (косвенное измерение). В этом случае необходимо произвести анализ уравнений материального и теплового баланса, которые позволяют выявить эту связь или использовать регрессионный анализ.

Определение периода опроса датчиков измеряемых величин

Период опроса существенно влияет на точность контроля. Рассмотрим способ определения периода опроса, основанный на определении автокорреляционной функции.

Пусть задана среднеквадратичная погрешность . Определение величины x ( t ). Требуется найти интервал времени T ₀ между замерами, при которых погрешность определение величины не превышало бы заданного значения. Методика основана на зависимости ошибки и автокорреляционной функции:

,

где — автокорреляционная функция.

,

где n — объем выборки, по которой определяется автокорреляционная функция.

, .

Сущность методики состоит в следующем:

1. Осуществляется съем данных с произвольным периодом опроса T ₀ (как можно меньше). Число точек опроса: 30-50. Полученные данные заносятся в таблицу:

Рекурсивный фильтр скользящего среднего

Да, дорогой читатель, такое тоже бывает, и может быть вкусно и полезно!

Как ты уже наверняка знаешь, дорогой читатель, существует два способа построения цифровых фильтров. Это рекурсивные фильтры, они же фильтры с бесконечной импульсной характеристикой (БИХ), и трансверсальные фильтры, они же фильтры с конечной импульсной характеристикой (КИХ). Самым простым и широко используемым фильтром КИХ является «фильтр скользящего среднего». Результат фильтрации такого фильтра, есть среднее арифметическое последних N отсчетов входного сигнала.

Или, в развернутом виде, для N=4:

Функция на языке С реализующая фильтр скользящего среднего:

Комплексный коэффициент передачи фильтра скользящего среднего, нормированный относительно частоты дискретизации, определится как преобразование Фурье от импульсной характеристики:

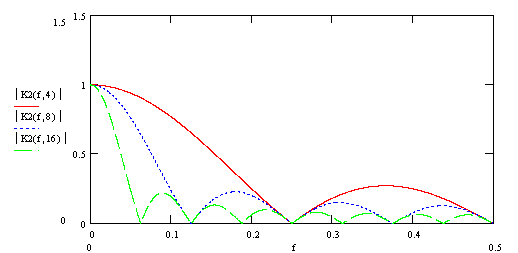
График амплитудно-частотной характеристики (АЧХ), нормированной относительно частоты дискретизации, при различных значениях длинны фильтра (N=4;8;16), приведен на рисунке:

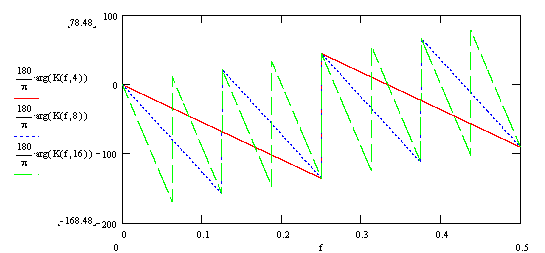
Соответственно, график фазо-частотной характеристики (ФЧХ):

Данный фильтр нашел широкое применение в обработке сигналов, отчасти благодаря своей простоте, но самое главное его свойство — линейная фазо-частотная характеристика, и, соответственно, постоянное во всей полосе частот время запаздывания сигнала. Этот фильтр трансформирует амплитудный спектр сигнала, не затрагивая фазовый, что делает удобным его использование в системах регулирования. Фильтр скользящего среднего, благодаря своей линейной переходной характеристике, широко применяется при линейной интерполяции, передискретизации сигнала и т.п.

Главный недостаток фильтра скользящего среднего — вычислительная сложность, пропорциональная длине фильтра N. Для решения этой проблемы существует рекурсивный фильтр скользящего среднего. То есть, фильтр, имеющий те же характеристики, что и классический фильтр скользящего среднего, но реализованный по рекурсивной схеме. Такие типы фильтров широко известны в узких кругах, и называются: рекурсивные фильтры с линейной ФЧХ [Введение в цифровую фильтрацию. Под. ред. Богнера Р. М: 1976] или CIC-фильтры [DspLib]. Существует научная школа проф. Турулина И.И. [РГБ], занимающаяся исследованием подобных фильтров.

Покажем способ построения рекурсивного фильтра скользящего среднего на примере фильтра длинной N=4. Впоследствии нетрудно будет обобщить результаты на произвольную длину фильтра.

Как было отмечено выше, значение n-ного отсчета сигнала на выходе фильтра можно определить как:

А значение предыдущего, ((n-1)-го) отсчета:

Вычтем из первого выражения второе, в результате получим:

Нетрудно сообразить, что при произвольной длине фильтра N, уравнение запишется в следующем виде:

(1)

На основании приведенного уравнения можно записать код фильтра на языке С, но сначала мы выполним проверку наших выкладок. Найдем частотные характеристики рекурсивного фильтра скользящего среднего, для чего выполним Z-преобразование уравнения фильтра. Хочу напомнить дорогому читателю, что для выполнения Z-преобразования необходимо заменить переменные (x_n,y_n) их Z-отображениями (X,Y), каждое понижение индекса переменной на единицу соответствует умножению Z -1 .

Решим полученное уравнение относительно Y/X –коэффициента передачи фильтра

Перейдем из Z-области в частотную область, заменив на , и получим комплексный коэффициент передачи:

Построим график модуля комплексного коэффициента передачи (АЧХ фильтра), при различных значениях N=4,8,16:

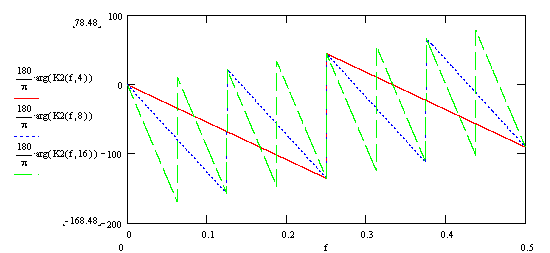
А также аргумент комплексного коэффициента передачи (ФЧХ фильтра):

Как видно из приведенных графиков, частотные характеристики классического фильтра скользящего среднего и рекурсивного фильтра скользящего среднего полностью совпадают.

Перейдем к реализации фильтра. При непосредственной реализации по уравнению фильтра (1) в условиях целочисленной арифметики возможны некоторые трудности. При выполнении операции деления на N в целочисленной арифметике возникает потеря значащих разрядов, что приводит к нелинейным искажениям сигнала на выходе фильтра. Для разрешения этих трудностей необходимо исключить операцию деления из рекуррентного уравнения фильтра. Для чего умножим обе части уравнения фильтра (1) на N.

В полученном выражении выполним подстановку:

В результате уравнение фильтра (1) преобразуется в систему уравнений:

На основании системы уравнений фильтра запишем код, реализующий фильтр на языке С.

Стоит отметить, что любители «совершенного кода» могут наложить ограничивающие требования на длину фильтра N. При длине фильтра, равной степеням двойки (2,4,8,16…), можно заменить операцию деления (/) арифметическим сдвигом (>>), операцию остаток от деления (%) — побитовой конъюнкцией (&).

Дорогой читатель, целью данной публикации не столько познакомить тебя с рекурсивным фильтром скользящего среднего, очень может быть, что ты про него прекрасно знаешь. Цель данной публикации познакомить тебя, дорогой читатель, с некоторыми практическими приемами анализа и синтеза цифровых фильтров. Посмотри, как просто мы перешли от трансверсального фильтра к рекурсивному, и Z-преобразование не так страшно, как его малюют. Надеюсь также, что метод повышения точности вычисления рекуррентных выражений в условиях целочисленной арифметики будет полезен тебе.

3.3.3. Фильтр скользящего среднего

Элементарным КИХ-фильтром является фильтр скользящего среднего (moving average), показанный на рис. 3.7. Фильтры скользящего среднего популярны для сглаживания данных, например, для анализа стоимости акций и т.д. Входные отсчеты x(n) пропускаются через ряд регистров памяти (помеченных z –1 в соответствии с представлением элемента задержки при z-преобразовании). В приведенном примере имеется четыре каскада, соответствующих 4-точечному фильтру скользящего среднего. Каждый отсчет умножается на 0,25, и результаты умножения суммируются для получения зна

чения скользящего среднего, которое подается на выход y(n). Общее уравнение фильтра скользящего среднего на N точек имеет вид:

Фильтр скользящего среднего работает по следующему алгоритму:

С учетом равенства коэффициентов, наиболее простой путь исполнения фильтра скользящего среднего можно представить следующим алгоритмом:

Первым шагом является запоминание первых четырех отсчетов x(0), x(1), x(2), x(3) в регистрах. Эти величины суммируются и затем умножаются на 0,25 для получения первого выхода y(3). Обратите внимание, что начальные значения выходов y(0), y(1) и y(2) некорректны, потому что, пока отсчет x(3) не получен, не все регистры заполнены.

Когда получен отсчет x(4), он суммируется с результатом, а отсчет x(0) вычитается из результата. Затем новый результат должен быть умножен на 0,25. Поэтому вычисления, требуемые для получения нового значения на выходе, состоят из одного суммирования, одного вычитания и одного умножения, независимо от длины фильтра скользящего среднего.

Таким образом, вычисление каждого выходного значения требует одного умножения, одного сложения, одного вычитания.

Реакция 4-точечного фильтра скользящего среднего на ступенчатое воздействие представлена на рис. 3.8. Фильтр скользящего среднего не имеет выброса по фронту входного сигнала. Это делает его полезным в приложениях обработки сигналов, где требуется фильтрация случайного белого шума при сохранении характера входного импульса. Из всех возможных линейных фильтров фильтр скользящего среднего дает самый низкий уровень шума при заданной крутизне фронта импульса. Существенно, что время реакции фильтра на ступенчатое воздействие от 0 % до 100 % равно произведению общего количества точек фильтра на период дискретизации.

Частотная характеристика простого фильтра скользящего среднего выражается функцией (рис. 3.9). Увеличение числа точек при реализации фильтра сужает основной лепесток, но существенно не уменьшает амплитуду боковых лепестков частотной характеристики, которая равна приблизительно -14 дБ для фильтра с 11 и с 31 отводами (длиной буфера). Естественно, эти фильтры не подходят в том случае, где требуется большое ослабление в полосе задержания.

Можно существенно улучшить эффективность простого КИХ-фильтра скользящего среднего, выбирая разные веса или значения коэффициентов вместо равных значений. Крутизна спада АЧХ может быть увеличена добавлением большего количества звеньев в фильтр, а характеристики полосы затухания улучшаются выбором надлежащих коэффициентов фильтра. В отличие от фильтра скользящего среднего, для реализации каждой ступени обобщенного КИХ-фильтра требуется цикл умножения с накоплением. Проектирование КИХ-фильтра сводится к выбору соответствующих коэффициентов и необходимого числа звеньев при формировании желаемой частотной харак

теристики фильтра fr/pic71_1.gif>. Для включения необходимой частотной характеристики в набор коэффициентов фильтра имеются различные алгоритмы и программные пакеты. Большинство этого программного обеспечения разработано для персональных компьютеров и доступно на рынке.

Ключевой теоремой проектирования КИХ-фильтра является утверждение, что коэффициенты h(n) КИХ-фильтра являются просто квантованными значениями импульсной характеристики этого фильтра. Соответственно, импульсная характеристика является дискретным преобразованием Фурье от .