Разностные схема для двумерного уравнения теплопроводности

Решение двумерного уравнения теплопроводности. Черногорский Вячеслав. 6 курс

Содержание

Цель [ править ]

Численное решение уравнения теплопроводности в единичном квадрате с помощью функций библиотеки MPI.

Постановка задачи [ править ]

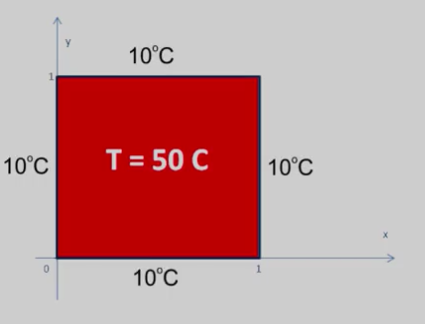
Имеется пластина в форме квадрата с ребром единичной длины. Пусть пластина разогрета до температуры Т_нач., и затем помещена в среду, которая имеет отличную температуру Т_среды. В этой задаче нас интересует процесс численного решения уравнения теплопроводности для пластины, которое выглядит следующим образом:

С граничными условиями

И начальным распределением температуры

[math]T(x,y,t) = 50 [/math]

Конечно-разностная схема [ править ]

Задача содержит производную по времени первого порядка и производные по пространственным координатам второго порядка. Запишем конечно-разностные аналоги слагаемых, входящих в уравнение

Уравнение теплопроводности

Ранее (см. разд. 2.1.2, 2.1.3) уже были построены и исследованы разностные схемы решения смешанной задачи для одномерного уравнения теплопроводности:

(2.75)

Были получены две двухслойные схемы — явная (2.3) и неявная (2.4). В явной схеме значения сеточной функции на верхнем (j + 1)-ом слое вычисляли с помощью решения на нижнем слое [соотношение (2.13)]. Для нахождения решения на (j + 1)-м слое по неявной схеме была получена трехдиагональная система линейных алгебраических уравнений (2.22), которую решают методом прогонки.

Неявная схема безусловно устойчива, явная схема устойчива при выполнении условия

Обе схемы сходятся к решению исходной задачи со скоростью .

Схемы (2.3), (2.4) построены для случая, когда значения искомой функции (температуры) Uна границах х = 0, х = 1определяются заданными функциями . Однако граничные условия в смешанной задаче (2.75) могут быть и иными, в них может входить производная искомой функции. Например, если конец стержня х=0 теплоизолирован, то условие имеет вид

В этом случае, как и при решении волнового уравнения, данное условие нужно записывать в схемах (2.3), (2.4) в разностном виде.

Перейдем теперь к построению разностных схем для уравнения теплопроводности с двумя пространственными переменными. Примем для простоты а = 1. Тогда это уравнение можно записать в виде

(2.76)

Пусть при t=0 начальное условие задано в виде

(2.77)

В отличие от волнового уравнения, требующего два начальных условия, в уравнение теплопроводности входит только первая производная по t, и необходимо задавать одно начальное условие.

Часто задачи теплопроводности или диффузии, описываемые двумерным уравнением (2.76), решаются в ограниченной области. Тогда, кроме начального условия (2.77), нужно формулировать граничные условия. В частности, если расчетная область представляет прямоугольный параллелепипед (рис. 2.24), то нужно задавать граничные условия на его боковых гранях. Начальное условие (2.77) задано на нижнем основании параллелепипеда.

Рис. 2.24. Расчетная область

Введем простейшую сетку с ячейками в виде прямоугольных параллелепипедов, для чего проведем три семейства плоскостей: хi= ih1(i=0,1. I), (j=0,1. J), . Значение сеточной функции в узлах обозначим символом . С помощью этих значений можно построить разностные схемы для уравнения (2.76).

Рассмотренные выше схемы для одномерного уравнения легко обобщаются на двумерный случай.

Построим явную разностную схему, шаблон которой изображен на рис. 2.25. Аппроксимируя производные отношениями конечных разностей, получаем следующее сеточное уравнение:

Рис. 2.25. Шаблон двумерной схемы

Отсюда можно найти явное выражение для значения сеточной функции на (k + 1)-ом слое:

(2.78)

Условие устойчивости имеет вид

(2.79)

При получается особенно простой вид схемы (2.78):

(2.80)

Полученная схема сходится со скоростью

Формулы (2.78) или (2.80) представляют собой рекуррентные соотношения для последовательного вычисления сеточной функции во внутренних узлах слоев k = 1,2. К. На нулевом слое используется начальное условие (2.77), которое записывается в виде

(2.81)

Значения в граничных узлах вычисляют с помощью граничных условий.

Алгоритм решения смешанной задачи для двумерного уравнения теплопроводности изображен на рис. 2.26. Здесь решение хранится на двух слоях: нижнем (массив ) и верхнем (массив ). Блоки граничных условий необходимо сформировать в зависимости от конкретного вида этих условий. Результаты выводят на каждом слое, хотя можно ввести шаг выдачи (см. рис. 2.13).

Рис. 2.26. Алгоритм решения двумерного уравнения теплопроводности

Построим теперь абсолютно устойчивую неявную схему для решения уравнения (2.76), аналогичную схеме (2.4) для одномерного уравнения теплопроводности. Аппроксимируя в (2.76) вторые производные по пространственным переменным на (k + 1)-ом слое, получаем следующее разностное уравнение:

(2.82)

Это уравнение можно записать в виде системы линейных алгебраических уравнений относительно значений сеточной функции на каждом слое:

(2.83)

К этой системе уравнений нужно добавить граничные условия для определения значений сеточной функции в граничных узлах (т.е. при i= 0, I; j = 0, J). На нулевом слое решение находится из начального условия (2.77), представленного в виде (2.81).

Система (2.83), полученная для двумерного уравнения теплопроводности, имеет более сложный вид, чем аналогичная система (2.22) для одномерного случая, которую можно решить методом прогонки. Таким образом, распространение неявной схемы на многомерный случай приводит к значительному усложнению вычислительного алгоритма и увеличению объема вычислений.

Недостатком явной схемы (2.78) является жесткое ограничение на шаг по времени τ, вытекающее из условия (2.79). Существуют абсолютно устойчивые экономичные разностные схемы, позволяющие вести расчет со сравнительно большим значением шага по времени и требующие меньшего объема вычислений. Две из них будут рассмотрены в разд. 2.3.3.

Метод геометрического параллелелизма и еще немного про MPI

Постановка задачи

Двумерное уравнение теплопроводности задается уравнением:

а также начальными условиями: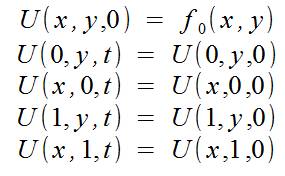

Также учитываем, что мы просчитываем ограниченную область пространства: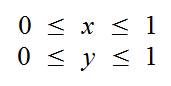

Итогом наших вычислений должен быть двумерный массив, содержащий значения функции U в узлах для некоторого значения времени. Можно решить уравнение аналитически, но это не наш вариант, и поэтому будем решать эту задачу численным методом. Для численного решения сделаем дискретизацию по времени, и получим координатную сетку в пространстве, а по времени получим набор «слоев». Для расчета будем использовать схему «крест».

Если не вдаваться в подробности этой схемы, то по значению во всех точках «креста» на некотором «временном слое» получим значение в центральной точке на «следующем временном слое». Причем шаги по времени и координатам должны быть согласованны:

(здесь и далее сетка фиксированная и шаги по пространственным координатам равны h)
Для экономии памяти можно хранить только две сетки по X и Y, одну для текущего временного слоя и для следующего временного слоя. В таком случае после рассчета следующего временного слоя этот слой становится текущим, а в массив прошлого слоя записываются значения следующего временного слоя.

Метод геометрического параллелелизма

Метод геометрического параллелелизма используется для задач в которых можно выделить некоторую геометрическую закономерность и использовать ее для разделения работы между процессорами. В этой задаче сетка для ограниченного пространства можно изобразить как:

Параллелелизм в этом случае прослеживается довольно хорошо и можно разделить массив на несколько, и каждый новый отдать на рассчет своему исполнителю.

Вообще-то можно разделить массив и на горизонтальные полосы, принципиальных различий для метода это не внесет, а про различия в реализации скажу позже. Таким образом каждый исполнитель будет считать только свой участок массива.

Подводные камни

Если вернуться к разностной схеме, по которой будем производить рассчет, то становится ясно, что это еще не конец. Из схемы видно, что для рассчета любого элемента сетки нам необходимо знать элементы сбоку от него на предыдущем слое. Это означает, что крайний слой пространственной сетки просчитать не сможем (так как не хватает данных), но если взглянуть на граничные условия, то видно что крайние элементы известны из условий. Но появляется проблема расчета элементов на границе областей исполнителей. Ясно, что придется в процессе пересылать данные между соседними исполнителями. Это можно сделать в виде цикла, который передает по элементу:

(подробнее про передачу по элементам можно прочитать в статьях, упомянутых в начале)
Этот способ не эффективен, поскольку придется устанавливать много соединений(это занимает большое время). Наши потребности может удовлетворить создание пользовательского типа данных. Кроме создания пользовательских структур, MPI может предложить нам несколько видов «масок» для данных: MPI_Type_contiguous и MPI_Type_vector. Первый из них создает тип, описывающий несколько элементов, подряд расположенных в памяти, а второй позволяет создать «шаблон» по которому из последовательно расположенных в памяти элементов выбираются «нужные» элементы, потом пропускаются «ненужные» и повторяется выбор нужных. Их количество фиксированное.

Если отправить этот тип, а в качестве *buf указать начало массива, то получится:
+ 0 0
+ 0 0
+ 0 0
Если указать как *buf второй элемент массива, то получим:
0 + 0
0 + 0
0 + 0

Так можно передать (и принять) только один столбец массива, причем за один вызов MPI_SEND:

Если расположить зоны исполнителей горизонтально, то можно использовать MPI_Type_contiguous или в MPI_Send указывать необходимое число элементов, но это, на мой взгляд, красивее.

Теперь надо понять в каком порядке пересылать эти столбцы. Самый очевидный: пусть исполнители по очереди передают нужный столбец нужному получателю. Тогда получим следующую картину: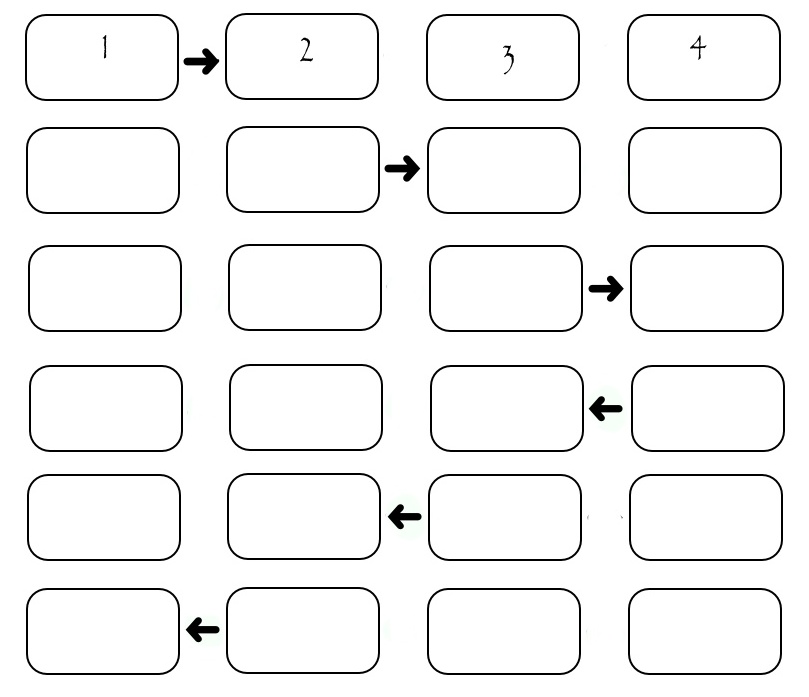

Хоть иллюстрация показывает обмен только между четырьмя исполнителями, можно посчитать, что если на одну передачу затрачивается некоторое SEND_TIME, то для передачи всех столбцов необходимо (2*N-2)*SEND_TIME. Видно, что во время передачи каждого столбца «работают» только два исполнителя, а остальные простаивают. Это не хорошо. Рассмотрим немного измененную схему: в ней исполнители разделены по «четности» их номера. Сначала все четные передают столбец исполнителю с большим номером, потом все четные передают столбец исполнителю с меньшим номером, потом аналогичным образом поступают исполнители с нечетными номерами. Конечно все пересылки происходят только при наличии того, кому пересылать.

В данном случае передача занимает ровно 4*SEND_TIME вне зависимости от количества исполнителей. На системах с множеством исполнителей это несет в себе значительное превосходство.

(На рисунках про передачу присутствует некоторая ложь: номера исполнителей начинаются с нуля, как в массиве, а на рисунках они пронумерованы в «обычном» порядке: начиная с первого. Т.е. отняв единицу от номера на рисунке получим его номер в программе)