Разностные уравнения для импульсной характеристики

Преобразование Лапласа дискретного сигнала. Z-преобразование. Разностное уравнение дискретного фильтра

DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов

Распространяется под лицензией LGPL v3

В предыдущих разделах мы подробно рассмотрели расчет аналоговых фильтров с заданными характеристиками. Пришло время переходить к анализу цифровых фильтров. Необходимо разделить понятия дискретного и цифрового фильтра.

Дискретным мы будем называть фильтр, импульсная характеристика которого является дискретной, а коэффициенты передаточной функции рассчитаны точно без ошибок округления.

Под цифровым фильтром мы будем понимать дискретный фильтр, коэффициенты передаточной характеристики которого рассчитаны не точно, а с ошибками округления вызванными конечной разрядностью представления числа.

На практике все рассчитанные фильтры являются цифровыми, так как разрядность представления числа ограничена. Однако использование компьютера позволяет производить операции с 64-битными числами с плавающей точкой, что минимизирует ошибки округления, поэтому можно предполагать, что рассчитанные с такой разрядностью фильтры «почти дискретные».

Важно отметить, что округление коэффициентов устойчивого дискретного фильтра, даже самое незначительное, может привести к неустойчивому цифровому фильтру. Поэтому при расчете фильтров, особенно фильтров высокого порядка, всегда необходимо проверять их устойчивость.

В цифровых системах сигналы представляют собой последовательности отсчетов, взятые, как правило, через равные промежутки времени . Ранее мы уже рассматривали модель дискретного сигнала :

Графически процесс дискретизации сигнала показан на рисунке 1.

Рассмотрим преобразование Лапласа дискретного сигнала :

Важное замечание. Если , то получаем дискретно-временное преобразование Фурье дискретного сигнала, при этом является периодической функцией частоты с периодом , кроме того, если , то

Кружочками условно показаны нули образа , а крестиками — полюсы.

Важно отметить, что периодичность дискретного преобразования Лапласа соответствует периодичности преобразования Фурье дискретного сигнала . Однако, как мы знаем из теории дискретного преобразования Фурье, на каждом периоде повторения спектр дискретного сигнала может быть искажен эффектом алиасинга, т.е. наложением «хвостов» исходной спектральной плотности из высших зон Найквиста (заполненная точками область на карте нулей и полюсов образа соответствует высшим зонам Найквиста).

В случае дискретного преобразования Лапласа эффект алиасинга сохраняется, и периодический образ на каждом периоде отличается от исходного образа . Так например, мы можем наблюдать алиасинг полюсов из высших зон Найквиста при неверном выборе частоты дискретизации. Если все полюсы исходного образа попадают в первую зону Найквиста, то при дискретизации они периодически разможатся, как это показано на рисунке 2.

Положение нулей дискретного преобразования Лапласа , как правило отличается от положения нулей исходного образа в результате эффекта алиасинга.

Рассмотрим процесс фильтрации дискретного сигнала . Согласно свойству преобразования Лапласа, процесс фильтрации во временно́й области сводится к умножению образа исходного сигнала на передаточную характеристику фильтра , которая в свою очередь, представляет преобразование Лапласа импульсной характеристики фильтра . Тогда преобразование Лапласа сигнала на выходе фильтра можно записать:

Первый случай. — образ дискретного сигнала, удовлетворяет (3), а — передаточная характеристика непрерывного фильтра, и свойство (3) не выполняется, значит также не удовлетворяето (3). Тогда можно сделать вывод о том, что при прохождении дискретного сигнала через аналоговый фильтр, выходной сигнал получается аналоговым. Аналоговый фильтр производит восстановление непрерывного сигнала по имеющемуся дискретному.

Второй случай. удовлетворяет (3), также удовлетворяет (3) (импульсная характеристика фильтра является дискретной), причем интервалы дискретизации сигнала и фильтра одинаковые и равны . Тогда в результате произведения также удовлетворяет (3). Таким образом, при прохождении дискретного сигнала через дискретный фильтр, выходной сигнал получается дискретным, с той же частотой дискретизации.

Третий случай. и удовлетворяют (3), но интервал дискретизации сигнала равен , а интервал дискретизации импульсной характеристики фильтра (исходный сигнал и и импульсная характеристика фильтра дискретизированы с разной частотой). В этом случае , в частных случаях, может удовлетворять (3), но период дискретизации выходного сигнала , будет равен «наименьшему общему кратному» периодов и . Заметим, что термин «наименьшее общее кратное» взят в кавычки, потому что и могут быть вещественными числами, в том числе и иррациональными. Тогда понимается как вещественное число, которое делится нацело как на , так и на . Например, если , а , то . Данный на практике не встречается, так как требует реализации цифровых схем, работающих на разных тактовых частотах. Разработка таких схем сопряжена с трудностями синхронизации при переходе данных из модулей, работающих на различных тактовых частотах.

Основное правило — для дискретных и цифровых фильтров интервалы дискретизации сигнала и фильтра должны быть равны.

Таким образом, для того чтобы на выходе фильтра получить дискретный сигнал, необходимо чтобы импульсная характеристика фильтра также была дискретной, а значит передаточная характеристика дискретного фильтра может быть представлена как результат дискретного преобразования Лапласа:

Если у дискретного фильтра количество коэффициентов ограничено, то такой фильтр называют фильтром с конечной импульсной характеристикой (КИХ-фильтром) [1] , а если количество коэффициентов бесконечно, то такой фильтр называют фильтром с бесконечной импульсной характеристикой (БИХ-фильтр) [2] .

При переходе от аналогового фильтра к цифровому, происходит периодическое размножение передаточной характеристики вдоль оси . При этом, переменная в образах дискретного преобразования Лапласа всегда присутствует только в показателе экспоненты, для обеспечения периодичности передаточных характеристик дискретных систем [1, стр 155].

В результате периодизации также происходит периодическое размножение нулей и полюсов, что доставляет некоторые неудобства. Для облегчения анализа вводят переменную вида:

Отображение не является конформным [2, стр. 145], потому что множество точек плоскости отображается в одну точку плоскости .

Графически отображение -плоскости в комплексную -плоскость показано на рисунке 3.

Рассмотрим некоторые особенности отображения (7).

Если , где , то для всех этих точек .

Если чисто вещественно, то и также вещественное, причем 0″/>. Заметим, что при , (внутри единичной окружности), а при величина (вне единичной окружности).

При , точка на мнимой оси плоскости отображается в точку , расположенную на единичной окружности и повернутой на угол рад. Таким образом, вся мнимая ось плоскости отображается в единичную окружность плоскости . Причем, один оборот единичной окружности соответствует от до рад/c.

Левая полуплоскость комплексной плоскости отображается внутрь единичной окружности плоскости . Действительно если , то представляет вектор длины повернутый на угол рад. При , длина вектора .

Правая полуплоскость комплексной плоскости отображается вне единичной окружности плоскости .

При переходе из комплексной -плоскости в комплексную -плоскость все бесконечно-повторяющиеся нули и полюса дискретного фильтра в -плоскости отображаются в конечное количество нулей и полюсов в -плоскости. Тогда выражение для передаточной характеристики дискретного фильтра может быть представлено при помощи подстановки (7) через конечное количество нулей и полюсов в -плоскости как:

Таким образом, главный вывод, который мы должны сделать заключается в следующем: при переходе от аналогового фильтра к дискретному, образ по Лапласу становится периодическим по мнимой оси, а количество нулей и полюсов фильтра бесконечным. Но при переходе в комплексную –плоскость мы получаем снова конечное количество нулей и полюсов, и соответственно конечное количество коэффициентов дискретного фильтра.

Рассмотрим некоторые свойства -преобразования. При этом мы будем рассматривать свойства относительно индексов отсчетов в предположении . В результате мы можем опустить период дискретизации в выражениях -преобразования.

Линейность. -образ суммы двух сигналов равен сумме -образов этих сигналов. Действительно, пусть есть два дискретных сигнала и , . Найдем -преобразование их суммы :

Можно показать, что данное свойство также справедливо и для циклической задержки ограниченной выборки сигнала:

Теорема о свертке. Пусть дано два сигнала ограниченной длительности и , . Найдем -преобразование их циклической свертки :

При выводе было использовано свойство циклической задержки -преобразования. Таким образом циклическая свертка сигналов соответствует произведению их -образов.

Аналогично, используя свойство задержки, можно показать, что -образ линейной свёртки сигналов равен произведению их -образов:

Ранее мы говорили о том, что пассивные аналоговые цепи описываются интегро-дифференциальными уравнениями непрерывного времени . При этом математический аппарат преобразования Лапласа позволяет перейти к алгебраическим уравнениям комплексной переменной при описании характеристик комплексных сопротивлений двухполюсников и передаточных функций четырехполюсников.

Ограничение количества пассивных элементов аналогового фильтра приводит к ограничению порядков интегро-дифференциальных уравнений и, соответственно, полиномов переменной при описании передаточных характеристик.

Прохождение сигнала через аналоговый фильтр описывается интегралом свертки входного сигнала и непрерывной импульсной характеристики , которая в свою очередь не может иметь произвольную форму при ограничении порядка аналогового фильтра, потому что является результатом решения интегро-дифференциальных уравнений ограниченного порядка.

Дискретные системы, в свою очередь, описываются разностными уравнениями дискретного времени . По аналогии с аналоговыми фильтрами, мы не можем требововать бесконечных порядков разностных уравнений, потому что это потребует бесконечных вычислительных ресурсов. Таким образом, мы должны ограничить порядки разностных уравнений, которые связывают выходной сигнал дискретного фильтра с входным сигналом , а также со значениями выходного сигнала на предыдущих тактах .

Заметим, что здесь мы также ведем рассмотрение относительно индексов отсчетов сигналов, в предположении c.

Общее разностное уравнение линейного цифрового фильтра имеет вид:

Временной индекс изменяется от до бесконечности, т.к. предполагается, что фильтр после включения может работать неограниченно долго.

Рассмотрим -преобразование разностного уравнения (16). -образ выходного сигнала равен:

Разностные уравнения для импульсной характеристики

21.6. ЦИФРОВЫЕ ФИЛЬТРЫ, ИХ РАЗНОСТНЫЕ УРАВНЕНИЯ, ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ИМПУЛЬСНЫЕ ХАРАКТЕРИСТИКИ

Цифровой фильтр описывается тремя характеристиками разностным уравнением , которому может быть поставлена в соответствие передаточная функция K ( z ) или полученная в результате обратного z -преобразования K ( z ) его дискретная импульсная характеристика h [ k ] . Из приведенных примеров следует, что существуют два принципиально различных класса цифровых фильтров. Фильтры первого класса нерекурсивные описываются разностным уравнением, в котором выходная величина y [ k ] выражается только через конечное число значений входного сигнала x [ n ] . Таким, например, является уравнение усреднения, рассмотренное выше.

Фильтры второго класса рекурсивные описываются уравнением, в котором выходная переменная y [ k ] выражается не только через значения входного сигнала x [ n ], но и через предшествующие значения выходного сигнала y [ k – m ] . Сюда, например, относится разностное уравнение u₂[ k + 1] = u₂[ k ] e -T/ t + u₁[ k ][h(T) – h(T – T_и)], описывающее преобразование прямоугольных сигналов RС -цепью (см. п. 20.4), а также дискретные модели любых других аналоговых динамических систем (в частности, электрических цепей).

Нерекурсивный цифровой фильтр сохраняет информацию о входном сигнале за конечное число шагов его импульсная характеристика конечна, а передаточная функция имеет вид ряда по степеням z (который включает и отрицательные показатели).

Информация, поступившая на вход рекурсивного фильтра, сохраняется в нем бесконечно долго; он имеет бесконечную по длительности импульсную характеристику и описывается передаточной функцией в виде рациональной дроби. Максимальная разность индексов переменных в разностном уравнении, который отвечает разность степеней z в числителе и знаменателе передаточной функции, определяет порядок цифрового фильтра.

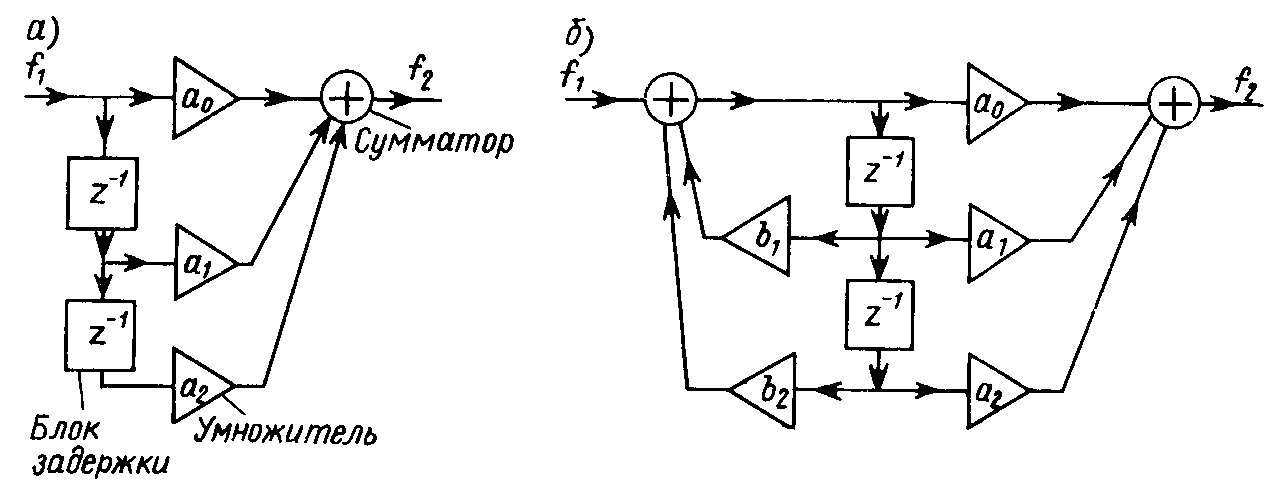
Так, нерекурсивный цифровой фильтр второго порядка описывается разностным уравнением f 2 [ n ] = a 0 f 1 [ n ] + a 1 f 1 [ n – 1] + a 2 f 1 [ n – 2], его передаточная функция K ( z ) = a 0 + a 1 z –1 + a 2 z –2 , а импульсная характеристика определяется коэффициентами, h [ n ] = a 0 , a 1 , a 2 , 0, 0, 0, 0, .

Рекурсивный цифровой фильтр второго порядка описывается разностным уравнением f 2 [ n ] = a 0 f 1 [ n ] + a 1 f 1 [ n – 1] + a 2 f 1 [ n – 2] + b 1 f 2 [ n – 1] + b 2 f 2 [ n – 2],

а его передаточная функция .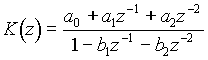

По известным значениям коэффициентов разностного уравнения a k и b k цифровой фильтр 2-го порядка может быть реализован с помощью умножителей, сумматоров и блоков задержки.

Блок-схемы цифровых фильтров обоих классов 2-го порядка, включающие перечисленные блоки, показаны на рис. 21.10 ( а – нерекурсивный; б – рекурсивный).

Математические основы цифровой обработки сигналов (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5

1.1 Определите разностное уравнение цепи y ( n ).

1.2 Определите с помощью разностного уравнения передаточную функцию и проверьте устойчивость цепи.

1.3 Определите импульсную характеристику цепи:

— с помощью передаточной функции (для нечетных вариантов)

— с помощью разностного уравнения цепи y ( n ) (для четных вариантов)

Построить график импульсной характеристики h ( n ).

Для достижения необходимой точности при вычислении импульсной характеристики надо учесть все отсчеты, значения которых превышают 10% от максимального значения .

1.4 Рассчитать амплитудно-частотную характеристику (АЧХ) и фазо-частотную характеристику (ФЧХ) цепи (с шагом ), построить графики АЧХ и ФЧХ.

2. Прохождение дискретного непериодического сигнала через ДЦ

На вход цепи подается непериодический сигнал .

2.1 Построить график дискретного сигнала.

2.2 Рассчитать спектр ДС с шагом . Построить амплитудный и фазовый спектр.

2.3 Определить сигнал на выходе цепи:

— по разностному уравнению (для нечетных вариантов)

— по формуле линейной свертки (для четных вариантов)

Построить график выходного сигнала.

2.4 Определить спектр сигнала на выходе цепи с шагом . Построить амплитудный и фазовый спектр.

3. Квантование в цифровых системах

3.1 Определите разрядность коэффициентов и , если допуск на отклонение системных характеристик составляет 1%

3.2 Рассчитайте шумы квантования на выходе цепи, полагая разрядность АЦП равной 8.

3.3 Рассчитайте масштабный множитель на входе цепи:

а) по условию ограничения максимума сигнала;

б) по условию ограничения энергии сигнала;

в) по условию ограничения максимума усиления цепи

Исходные данные:

1. Исследование характеристик дискретной цепи

Известно, что дискретной цепью называют любую систему (цепь) преобразующую одну последовательность х( n ) в другую последовательность y ( n ). Будем считать, что дискретная цепь обладает свойством линейности (выходная реакция на сумму дискретных сигналов равна сумме реакций на эти сигналы) и свойством стационарности (задержка входного дискретного сигнала приводит лишь к такой же задержке выходного дискретного сигнала).

Важно помнить, что:

— в схеме не указывают умножители, коэффициенты которых равны 0;

— умножители, коэффициенты которых равны 1, в схеме представляют собой короткозамкнутый проводник.

Изобразим дискретную цепь с заданными коэффициентами (см. рис. 1.1):

Рисунок 1.1 – Дискретная рекурсивная цепь второго порядка

1.1 Разностное уравнение дискретной цепи

Если известны параметры линейной дискретной системы, то взаимосвязь между входным воздействием x ( n ) и реакцией y ( n ) описывается разностным уравнением вида:

, (1.1)

где , — коэффициенты уравнения (вещественные константы);

x ( n ), y ( n ) — воздействие и реакция (вещественные или комплексные сигналы);

N — число прямых связей;

L — число обратных связей;

, — воздействие и реакция, задержанные на i и периодов дискретизации соответственно.

Важно помнить, что:

— разностное уравнение должно отображать все пути прохождения входного сигнала через цепь.

Запишем разностное уравнение дискретной цепи, изображенной на рис. 1.1:

(1.2)

1.2 Определение передаточной функции цепи

Известно, что передаточной функцией Н( z ) называют отношение z -изображения реакции к z -изображению воздействия при нулевых начальных условиях.

Применив z -преобразования к разностному уравнению, получим:

Тогда передаточная характеристика цепи:

(1.3)

Запишем передаточную функцию дискретной цепи, изображенной на рис.1.1:

(1.4)

Дискретная цепь является устойчивой, если полюсы ее передаточной функции лежат внутри единичной окружности z -плоскости, т. е.

(1.5)

Чтобы определить, устойчива ли дискретная цепь, показанная на рис.1.1, найдем ее полюсы. Для этого приравняем знаменатель передаточной функции к нулю:

По полученным результатам видно, что условие (1.5) выполняется, т. е. дискретная цепь является устойчивой.

1.3 Определение импульсной характеристики цепи h ( n )

Импульсной характеристикой h ( n ) линейной дискретной цепи называется ее реакция на дискретную дельта-функцию δ( n ) при нулевых начальных условиях.

(1.6)

Признаком нулевых начальных условий является отсутствие реакции при отсутствии воздействия.

Важно помнить, что:

— как и разностное уравнение, импульсная характеристика описывает дискретную цепь во временной области;

— определить импульсную характеристику дискретной системы можно двумя способами:

1. по разностному уравнению, решая его методом прямой подстановки;

2. по передаточной функции путем деления полинома числителя на знаменатель

— импульсная характеристика нерекурсивной цепи имеет конечную длительность, значения отсчетов равны коэффициентам разностного уравнения;

— импульсная характеристика рекурсивной цепи имеет бесконечную длительность;

— для достижения необходимой точности при вычислении импульсной характеристики надо учесть все отсчеты, значения которых превышают 10% от максимального значения .

1 способ: (для четных вариантов)

Допустим, что на вход дискретной цепи действует дельта-функция вида . Тогда, согласно разностному уравнению цепи:

(1.7)

Так как составляет ≈ 8,5 % от , т. е. не превышает 10%, дальнейшие отчеты импульсной характеристики цепи считать не имеет смысла.

2 способ: (для нечетных вариантов)

Импульсную характеристику дискретной цепи можно найти по передаточной функции, выполнив ее обратное z -преобразование. Обратное z -преобразование передаточной функции можно осуществить путем последовательного деления полинома числителя Н( z ) на знаменатель с поочередным выделением слагаемых вида .