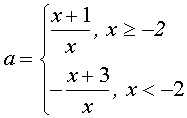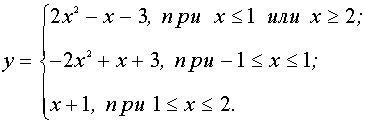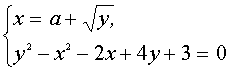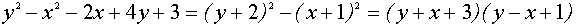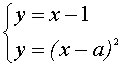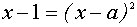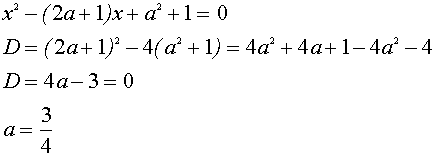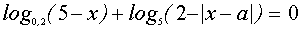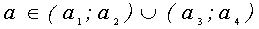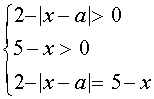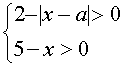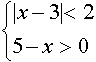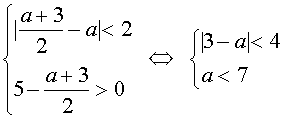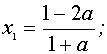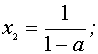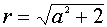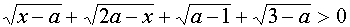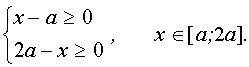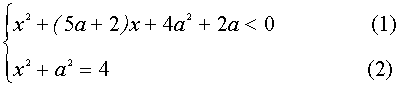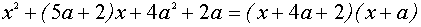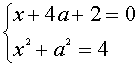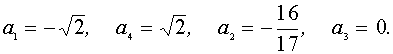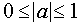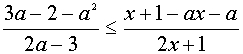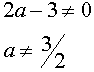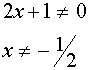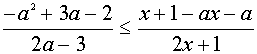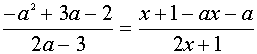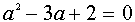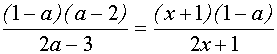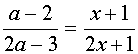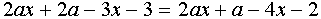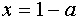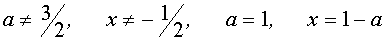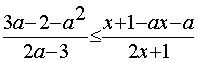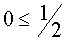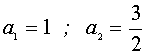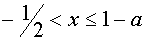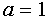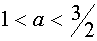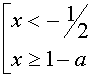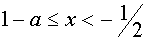5rik.ru
Материалы для учебы и работы
Реферат: Графическое решение уравнений, неравенств, систем с параметром
II. Уравнения с параметрами.
§ 2. Алгоритм решения.
III. Неравенства с параметрами.
§ 2. Алгоритм решения.
IV. Список литературы.
Изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами. Некоторые Вузы также включают в экзаменационные билеты уравнения, неравенства и их системы, которые часто бывают весьма сложными и требующими нестандартного подхода к решению. В школе же этот один из наиболее трудных разделов школьного курса математики рассматривается только на немногочисленных факультативных занятиях.
Готовя данную работу, я ставил цель более глубокого изучения этой темы, выявления наиболее рационального решения, быстро приводящего к ответу. На мой взгляд графический метод является удобным и быстрым способом решения уравнений и неравенств с параметрами.
В моём реферате рассмотрены часто встречающиеся типы уравнений, неравенств и их систем, и, я надеюсь, что знания, полученные мной в процессе работы, помогут мне при сдаче школьных экзаменов и при поступлении а ВУЗ.
§ 1. Основные определения
¦ (a, b, c, …, k , x)=j (a, b, c, …, k , x), (1)
где a, b, c, …, k , x -переменные величины.
Любая система значений переменных
а = а0, b = b0, c = c0, …, k = k0, x = x0,
при которой и левая и правая части этого уравнения принимают действительные значения, называется системой допустимых значений переменных a, b, c, …, k , x. Пусть А – множество всех допустимых значений а, B – множество всех допустимых значений b, и т.д., Х – множество всех допустимых значений х, т.е. аÎ А, bÎ B, …, xÎ X. Если у каждого из множеств A, B, C, …, K выбрать и зафиксировать соответственно по одному значению a, b, c, …, k и подставить их в уравнение (1), то получим уравнение относительно x, т.е. уравнение с одним неизвестным.
Переменные a, b, c, …, k , которые при решении уравнения считаются постоянными, называются параметрами, а само уравнение называется уравнением, содержащим параметры.
Параметры обозначаются первыми буквами латинского алфавита: a, b, c, d, …, k , l, m, n а неизвестные – буквами x, y,z.
Решить уравнение с параметрами – значит указать, при каких значениях параметров существуют решения и каковы они.
Два уравнения, содержащие одни и те же параметры, называются равносильными, если:
а) они имеют смысл при одних и тех же значениях параметров;
б) каждое решение первого уравнения является решением второго и наоборот.
§ 2. Алгоритм решения. Находим область определения уравнения. Выражаем a как функцию от х. В системе координат хОа строим график функции а=¦ (х) для тех значений х, которые входят в область определения данного уравнения.
Находим точки пересечения прямой а=с, где сÎ (-¥ ;+¥ ) с графиком функции а=¦ (х).Если прямая а=с пересекает график а=¦ (х), то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение а=¦ (х) относительно х.
Записываем ответ. § 3. Примеры
I. Решить уравнение
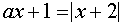
Поскольку х=0 не является корнем уравнения, то можно разрешить уравнение относительно а :

График функции – две “склеенных” гиперболы. Количество решений исходного уравнения определяется количеством точек пересечения построенной линии и прямой у=а.
Если а Î (-¥ ;-1]È (1;+¥ )È 

Таким образом, на этом промежутке уравнение (1) имеет решение 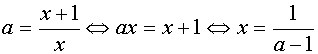
Если а Î 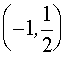
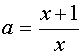
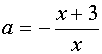
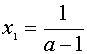
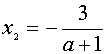
Если а Î 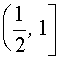
Если а Î (-¥ ;-1]È (1;+¥ )È 
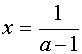
Если а Î 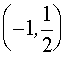
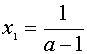
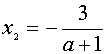
Если а Î 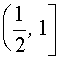
II. Найти все значения параметра а, при которых уравнение 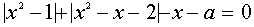
Переписав уравнение в виде 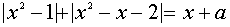

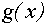
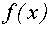
В системе координат хОу построим график функции 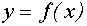
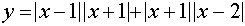
Поскольку график функции 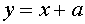

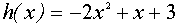
Ответ: 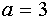
III. Найти все значения параметра а, при каждом из которых система уравнений
Из первого уравнения системы получим 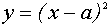
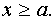
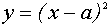
Выделим в левой части второго уравнения полные квадраты и разложим её на множители
Множеством точек плоскости 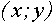
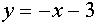
Выясним, при каких значениях параметра а кривая из семейства “полупарабол” имеет хотя бы одну общую точку с одной из полученных прямых.
Если вершины полупарабол находятся правее точки А, но левее точки В (точка В соответствует вершине той “полупараболы”, которая касается
прямой 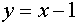
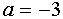
Случай касания “полупараболы” с прямой 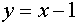
В этом случае уравнение
имеет один корень, откуда находим :
Следовательно, исходная система не имеет решений при 
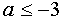
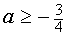
Ответ: а Î (-¥ ;-3] È (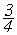
IV. Решить уравнение
Использовав равенство 
Это уравнение равносильно системе
Уравнение 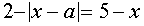
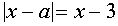
Последнее уравнение проще всего решить, используя геометрические соображения. Построим графики функций 

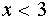
Если 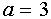
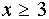
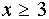
При 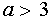
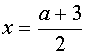
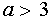
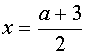
Исследуем теперь, при каких значениях а найденные решения уравнения (*) будут удовлетворять условиям
Пусть 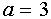
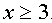
Её решением будет промежуток хÎ (1;5). Учитывая, что 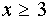
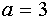
Рассмотрим случай, когда 
Решив эту систему, найдем аÎ (-1;7). Но 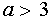
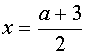
если аÎ (-¥ ;3), то решений нет;
если а=3, то хÎ [3;5);
если aÎ (3;7), то 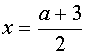
если aÎ [7;+ ¥ ), то решений нет.
V. Решить уравнение
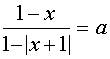
При любом а : 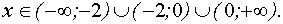
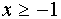
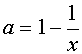
если 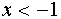
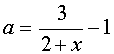
Строим график функции 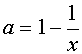

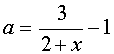
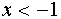
если 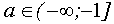
если 

если 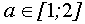
если 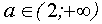
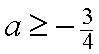
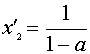
VI. Каким условиям должны удовлетворять те значения параметров 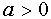
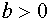
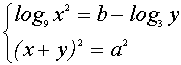

имеют одинаковое число решений ?
С учетом того, что 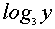
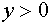
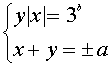
равносильную системе (1).
Система (2) равносильна системе
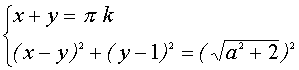
Первое уравнение системы (4) задает в плоскости хОу семейство прямых, второе уравнение задает семейство концентрических окружностей с центром в точке А(1;1) и радиусом
Поскольку 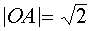
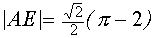
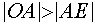
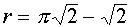
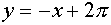
Таким образом, если 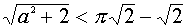
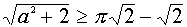
Если же иметь в виду не радиусы окружностей, а сам параметр а, то система (4) имеет четыре решения в случае, когда 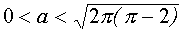
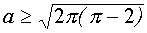
Обратимся теперь к рассмотрению системы (3). Первое уравнение этой системы задаёт в плоскости хОу семейство гипербол, расположенных в первом и втором квадрантах. Второе уравнение системы (3) задает в плоскости хОу семейство прямых.
При фиксированных положительных а и b система (3) может иметь два, три, или четыре решения. Число же решений зависит от того, будет ли прямая, заданная уравнением 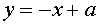
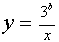
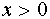
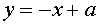
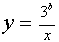
Для решения этого рассмотрим уравнение
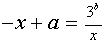
которое удобнее переписать в виде
Теперь решение задачи сводится к рассмотрению дискриминанта D последнего уравнения:
если 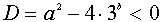
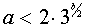
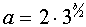
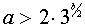
Таким образом, одинаковое число решений у систем (1) и (2) – это четыре. И это имеет место, когда 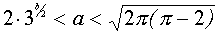
Ответ:
II. Неравенства с параметрами. § 1. Основные определения
¦ (a, b, c, …, k , x)>j (a, b, c, …, k , x), (1)
где a, b, c, …, k – параметры, а x – действительная переменная величина, называется неравенством с одним неизвестным, содержащим параметры.
Любая система значений параметров а = а0, b = b0, c = c0, …, k = k0, при некоторой функции
имеют смысл в области действительных чисел, называется системой допустимых значений параметров.
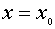
принимают действительные значения при любой допустимой системе значений параметров.
Множество всех допустимых значений х называется областью определения неравенства (1).
Действительное число х0 называется частным решением неравенства (1), если неравенство
¦ (a, b, c, …, k , x0)>j (a, b, c, …, k , x0)
верно при любой системе допустимых значений параметров.
Совокупность всех частных решений неравенства (1) называется общим решением этого неравенства.
Решить неравенство (1) – значит указать, при каких значениях параметров существует общее решение и каково оно.
¦ (a, b, c, …, k , x)>j (a, b, c, …, k , x) и (1)
z (a, b, c, …, k , x)>y (a, b, c, …, k , x) (2)
называются равносильными, если они имеют одинаковые общие решения при одном и том же множестве систем допустимых значений параметров.
§ 2. Алгоритм решения. Находим область определения данного неравенства. Сводим неравенство к уравнению. Выражаем а как функцию от х. В системе координат хОа строим графики функций а =¦ (х) для тех значений х, которые входят в область определения данного неравенства. Находим множества точек, удовлетворяющих данному неравенству. Исследуем влияние параметра на результат. найдём абсциссы точек пересечения графиков. зададим прямую а=соnst и будем сдвигать её от -¥ до+¥ Записываем ответ.
Это всего лишь один из алгоритмов решения неравенств с параметрами, с использованием системы координат хОа. Возможны и другие методы решения, с использованием стандартной системы координат хОy.
I. Для всех допустимых значений параметра а решить неравенство
В области определения параметра а, определённого системой неравенств
данное неравенство равносильно системе неравенств
Если 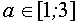
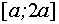
Ответ: 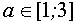
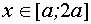
II. При каких значениях параметра а имеет решение система
Найдем корни трехчлена левой части неравенства –
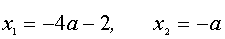
Прямые, заданные равенствами (*), разбивают координатную плоскость аОх на четыре области, в каждой из которых квадратный трехчлен
сохраняет постоянный знак. Уравнение (2) задает окружность радиуса 2 с центром в начале координат. Тогда решением исходной системы будет пересечение заштрихован
ной области с окружностью, где 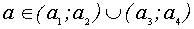
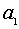
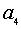
а значения 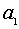
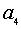
Решая эти системы, получаем, что
Ответ:
III. Решить неравенство 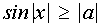
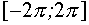
Находим область допустимых значений – 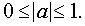
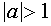
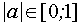
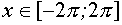
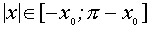
Ответ: Решения неравенства существуют при
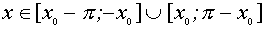


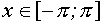
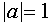
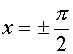
IV. Решить неравенство
Находим ОДЗ или линии разрыва (асимптоты)
Найдем уравнения функций, графики которых нужно построить в ПСК; для чего перейдем к равенству :
Разложим числитель на множители.
т. к. 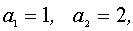
Разделим обе части равенства на 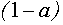
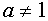
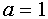
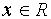
3. Строим в ПСК хОа графики функций
и нумеруем образовавшиеся области (оси роли не играют). Получилось девять областей.
4. Ищем, какая из областей подходит для данного неравенства, для чего берем точку из области и подставляем в неравенство.
Для наглядности составим таблицу.
точка
неравенство:
вывод
5. Найдем точки пересечения графиков
6. Зададим прямую а=сonst и будем сдвигать её от -¥ до +¥ .
при
при
при
при 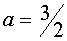
при
«Графические методы решения уравнений и неравенств с параметрами»
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ИНСТИТУТ РАЗВИТИЯ ОБРАЗОВАНИЯ
«Графические методы решения уравнений и неравенств с параметрами»
1. ГРАФИЧЕСКИЕ ПРИЕМЫ. КООРДИНАТНАЯ ПЛОСКОСТЬ (х;у) 4
1.1. Параллельный перенос. 5
1.3. Гомотетия. Сжатие к прямой. 13
1.4. Две прямые на плоскости. 15
2. ГРАФИЧЕСКИЕ ПРИЕМЫ. КООРДИНАТНАЯ ПЛОСКОСТЬ (х;а) 17
БИБЛИОГРАФИЧЕСКИЙ СПИСОК. 22
Проблемы, возникающие у школьников при решении нестандартных уравнений и неравенств, вызваны как относительной сложностью этих задач, так и тем, что в школе, как правило, основное внимание уделяется решению стандартных задач.
Многие школьники воспринимают параметр как «обычное» число. Действительно, в некоторых задачах параметр можно считать постоянной величиной, но эта постоянная величина принимает неизвестные значения! Поэтому необходимо рассматривать задачу при всех возможных значениях этой постоянной величины. В других задачах бывает удобно искусственно объявить параметром одну из неизвестных.
Иные школьники относятся к параметру как к неизвестной величине и, не смущаясь, могут выразить в ответе параметр через переменную х.
На выпускных и вступительных экзаменах встречаются, в основном, два типа задач с параметрами. Вы сразу отличите их по формулировке. Первый: «Для каждого значения параметра найти все решения некоторого уравнения или неравенства». Второй: «Найти все значения параметра, при каждом из которых для данного уравнения или неравенства выполняются некоторые условия». Соответственно и ответы в задачах этих двух типов различаются по существу. В ответе к задаче первого типа перечисляются все возможные значения параметра и для каждого из этих значений записываются решения уравнения. В ответе к задаче второго типа указываются все значения параметра, при которых выполняются условия, указанные в задаче.
Решением уравнения с параметром для данного фиксированного значения параметра называется такое значение неизвестной, при подстановке которого в уравнение, последнее обращается в верное числовое равенство. Аналогично определяется решение неравенства с параметром. Решить уравнение (неравенство) с параметром — это значит для каждого допустимого значения параметра найти множество всех решений данного уравнения (неравенства).
1. ГРАФИЧЕСКИЕ ПРИЕМЫ. КООРДИНАТНАЯ ПЛОСКОСТЬ (х;у)
Наряду с основными аналитическими приемами и методами решений задач с параметрами существуют способы обращения к наглядно-графическим интерпретациям.
В зависимости от того какая роль параметру отводится в задаче (неравноправная или равноправная с переменной), можно соответственно выделить два основных графических приема: первый – построение графического образа на координатной плоскости (х ; у), второй – на (х ; а).
На плоскости (х ; у) функция у =f (х ; а) задает семейство кривых, зависящих от параметра а. Понятно, что каждое семейство f обладает определенными свойствами. Нас же в первую очередь будет интересовать, с помощью какого преобразования плоскости (параллельный перенос, поворот и т. д.) можно перейти от одной кривой семейства к какой-либо другой. Каждому из таких преобразований будет посвящен отдельный пункт. Как нам кажется, подобная классификация облегчает решающему поиск необходимого графического образа. Отметим, что при таком подходе идейная часть решения не зависит от того, какая фигура (прямая, окружность, парабола и т. п.) будет являться членом семейства кривых.
Разумеется, не всегда графический образ семейства у = f (х ; а) описывается простым преобразованием. Поэтому в подобных ситуациях полезно сосредоточить внимание не на том, как связаны кривые одного семейства, а на самих кривых. Иными словами можно выделить еще один тип задач, в которых идея решения прежде всего основана на свойствах конкретных геометрических фигур, а не семейства в целом. Какие же фигуры (точнее семейства этих фигур) нас будут интересовать в первую очередь? Это прямые и параболы. Такой выбор обусловлен особым (основным) положением линейной и квадратичной функций в школьной математике.
Говоря о графических методах, невозможно обойти одну проблему, «рожденную» практикой конкурсного экзамена. Мы имеем в виду вопрос о строгости, а следовательно, о законности решения, основанного на графических соображениях. Несомненно, с формальной точки зрения результат, снятый с «картинки», не подкрепленный аналитически, получен нестрого. Однако кем, когда и где определен уровень строгости, которого следует придерживаться старшекласснику? По нашему мнению, требования к уровню математической строгости для школьника должны определяться здравым смыслом. Мы понимаем степень субъективности такой точки зрения. Более того, графический метод – всего лишь одно из средств наглядности. А наглядность может быть обманчивой. Так, для графиков функций 
1.1. Параллельный перенос.
Начнем с задач, где членами семейства у = f (х ; а) будут прямые.
Пример 1. Найти все значения параметра b, при которых уравнение 
Решение. Для удобства обозначим lg b = а. Запишем уравнение, равносильное исходному: 
Строим график функции 


Ответ. 
Пример 2. Для каждого значения параметра 

Решение. Построим график функции 
Рассмотрим 
Ответ. Если 
если 
если 
если 
Перейдем к новой серии задач. Будем рассматривать семейства кривых, задаваемые уравнениями 
Пример 3. Решить неравенство 
Решение. Построим прямую у = х +1 (рис. 3). Если «полупарабола» 
иметь одно решение, что равносильно для уравнения (х+1)2 = х + а иметь один корень. Отсюда получаем 

Далее, смещая «полупараболу» влево, зафиксируем последний момент, когда графики у = х + 1 и 
Ясно, что при 


Когда «полупарабола» и прямая пересекаются только в одной точке (это соответствует случаю а > 1), то решением будет отрезок [-а ; х2′], где х2′ – больший из корней х1 и х2 (положение IV).
Пример 4. Сколько корней имеет уравнение 
Решение, Заметим, что, введя функции 



Рассмотрим функции 





Ответ. Если 

Сразу отметим, что в настоящем пункте выбор семейства кривых (в отличие от самих задач) не отличается разнообразием, а точнее он одновариантный: во всех примерах члены семейства у = f (х;а) – прямые. Более того, центр поворота принадлежит прямой. Иными словами, мы ограничимся семейством вида у – у0 = а (х – х0), где (х0 ; y0) – центр поворота.
Такой выбор обусловлен тем, что в равенстве f (х, у,а) = 0 очень сложно увидеть аналитическое задание поворота кривых, отличных от прямых. Поэтому о повороте как о методе целесообразно говорить лишь для прямых указанного типа.
Пример 5. Найти все значения параметра к, при которых система уравнений
Решение. Ясно, что прямые семейства 


На рис. 5 отмечены два положения прямой, которым соответствуют некоторые значения параметра k1 и k2. На первой прямой лежит вершина. Вторая прямая касается «полупараболы». Наглядно очевидно, что если прямые семейства «заметают» образовавшийся угол (параметр k изменяется от k1 и k2), то исходная система имеет решения.
Значение k1 найдем, подставив в первое уравнение системы пару (0;0). Отсюда k1 =-1/4. Значение k2 получим, потребовав от системы
иметь одно решение, что равносильно для уравнения 
Ответ. 
Сделаем одно замечание. В некоторых примерах этого пункта нам придется решать стандартную задачу: для прямой семейства находить ее угловой коэффициент, соответствующий моменту касания с кривой. Покажем, как это сделать в общем виде при помощи производной.
Если (х0 ; y0) = центр поворота, то координаты (х1; у1) точки касания с кривой у = f (х) можно найти, решив систему
Искомый угловой коэффициент k равен 
Пример 6. При каких значениях параметра 

Решение. Рассмотрим функцию 



Все лучи проходящие между ОА и ОВ пересекают дугу АВ в одной точке, также в одной точке пересекают дугу АВ ОВ и ОМ (касательная). Угловые коофициенты ОА и ОВ равны соответственно 


Итак, прямые семейства 

Ответ. 
Пример 7. При каких 

Решение. Рассмотрим функцию 



Функция же 





Ответ. При 

1.3. Гомотетия. Сжатие к прямой.
Пример 8. Сколько решений имеет система
в зависимости от значений параметра а?
Решение. Прежде всего отметим, что при 

Обратимся к рис. 8. Очевидно если квадрат находится внутри окружности 



Реферат » Решение уравнений и неравенств графическим способом» ( 9 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
МБОУ Алтайская СОШ №1
Тема : « Графическое решение уравнений и неравенств»
Учащаяся 9 а класса
МБОУ Алтайская СОШ №1
Бабаева Галина Яковлевна,
МБОУ Алтайской СОШ №1
С. Алтайское , Алтайский район, 2019 год.
II . Основная часть
2. Как графически решить уравнение________________________стр.4
3. Какие бывают функции ?________________________________стр.4
4. Графическое решение линейного уравнения с одной переменной.стр.5
5. Решение квадратного уравнения графическим способом._____ стр6-8
6. Графическое решение смешанных уравнений._______________стр.8-12. 7. Решение квадратных неравенств графическим способом_______стр.13
8. Решение линейных неравенств графическим способом стр 14
IV . Список литературы______________________________________стр.16
Цель моей работы – изложить графический метод решения уравнений и неравенств, который дает возможность определить корни или доказать ,что уравнение корней не имеет ( или решением неравенства является пустое множество).
Актуальность темы : графический метод, опирающийся на знания элементарных функций, удобно применять при решении задач на нахождение числа корней и на нахождение корней уравнений.
Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решать многие задачи и порой является единственным средством решения. Кроме того, умение строить графики функций представляет большой самостоятельный интерес. В данной исследовательской работе я показала как наиболее удобным способом преобразовывать уравнения . чтобы сводить к построению элементарных функций.
Часто построение графиков связано с исследованием поведения функций. Однако необходимость построения графиков не ограничивается только этим. В ряде случаев графики облегчают нахождение решений уравнений и неравенств, сокращая и упрощая аналитические выкладки, и часто при этом являются единственным методом решения таких задач. Данный метод может использоваться не только для одиночных уравнений, но и для их систем, а также неравенств
Уравнение – выражение, содержащее переменную.
Решить уравнение – это значит найти все его корни, или доказать, что их нет.
Корень уравнения – это число, при подстановке которого в уравнение получается верное числовое равенство.
График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргументов, а ординаты – соответствующим значениям функции.
Решение уравнений графическим способом позволяет найти точное или приближенное значение корней, позволяет найти количество корней уравнения.
При построении графиков и решении уравнений используются свойства функции, поэтому метод чаще называют функционально-графическим. Графиком функции y = f(x) называется множество всех точек
Заметим , что так как функция f сопоставляет каждому x D(f) одно число f(x) , то график функции f пересекается любой прямой, параллельной оси ординат, не более, чем в одной точке. И наоборот: всякое непустое множество точек плоскости, имеющее со всякой прямой, параллельной оси ординат, не более одной общей точки, является графиком некоторой функции.
Не всякое множество точек координатной плоскости является графиком какой-либо функции. Например, множество точек окружности не может быть графиком функции, поскольку значению абсциссы внутри окружности, соответствует два значения ординаты.
В общем случае уравнение с одной переменой х можно записать в виде f(x)=g(x),где f(x) и g(x) — некоторые функции. Функция f(x) является левой частью , а g(x) — правой частью уравнения.
Тогда для решения уравнения необходимо построить в одной системе координат графики функций f(x) и g(x). Абсциссы точек пересечения будут являться решениями данного уравнения.
Использование монотонности функций при решении уравнений: если функция 


2. Как графически решить уравнение.
Иногда уравнения решают графическим способом. Для этого надо преобразовать уравнение так (если оно уже не представлено в преобразованном виде), чтобы слева и справа от знака равенства стояли выражения, для которых легко можно нарисовать графики функций. Графическим решением уравнения являются абсциссы точек пересечения графиков построенных функций. Графики могут пересекаться в нескольких точках, в одной точке, вообще не пересекаться. Отсюда следует, что уравнение может иметь несколько корней, или один корень, или вообще их не иметь.
3. Какие бывают функции .
Линейная функция задаётся уравнением у = k*x+ b , где k и b – некоторые числа. Графиком этой функции является прямая. Для построения прямой достаточно в таблице значений взять только две точки. Это вытекает из аксиомы планиметрии
Функция обратной пропорциональности у =k/x , где. График этой функции называется гиперболой.
Функция (х– a)^2+ (у – b)^2 = r^2 , где а , b и r – некоторые числа. Это окружность радиуса r с центром в т. А ( а , b ).
Квадратичная функция y = a *х 2 + b*x+ c , где а, b, с – некоторые числа и
а не равно 0. Графиком этой функции является парабола.
Графики линейных функций, содержащих выражение под знаком модуля.
Для построения графиков функций, содержащих выражение под знаком модуля, сначала находят корни выражений, стоящих под знаком модуля. Эти корни разбивают числовую прямую на промежутки. График строят в каждом промежутке отдельно.
В простейшем случает, когда только одно выражение стоит под знаком модуля и нет слагаемых без знака модуля, можно построить график функций,
опустив знак модуля, а затем часть графика, расположенного в области отрицательных значений y , отобразить симметрично оси ОХ.
Элементарная функций, содержащая модуль :
4. Графическое решение линейного уравнения с одной переменной.
Как мы уже знаем, графиком линейного уравнения является прямая линия, отсюда и название данного вида. Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и уравнение решено. Мы нашли корень .А я покажу , как это сделать графическим способом.
Задание . Решить графическим способом уравнение : 2 x − 10 = 2
1)Перенесем слагаемые следующим образом: 2 x = 12.
2) Построим графики функций: y=2x и y=12.
Но можно решать и по-другому.
Для рассмотрения альтернативного решения вернемся к нашему уравнению:
Построим графики функций: y=2 x − 10 y =2
5. Решение квадратного уравнения графическим способом.
Для этого преобразуем уравнение к виду: х 2 =-2x+8 . Построим графики функций: у = -2x+8 и у = х 2
Получим точки пересечения графиков данных функций.
В ответ запишем абсциссы этих точек : x = -4 и x =2.
Данное уравнение можно решить , переписав уравнение следующим образом: x^2 – 8 = -2x
Тогда будем строить графики функций: y = x^2 – 8 и y = -2x.
А также уравнение можно решить , переписав следующим образом:
Тогда будем строить графики следующих функций : y = x^2 + 2x и y = 8 .
При этом абсциссы точек пересечения графиков будут одинаковые :
Задание. Решить уравнение: x² – 2x = 0
Перепишем уравнение в виде : x² = 2x
Построим графики функций y = x² и y = 2 и найдем точки их пересечения :
Задание. Решить уравнение: х 2 +2=0
Преобразуем так: х 2 = -2
Построим графики функций: у=-2 и у= х 2
Графики функций не пересекаются ,поэтому уравнение решений не имеет.
Ответ : решений нет.
6. Графическое решение смешанных уравнений.
Задание. Решить уравнение: 3/х +2 =х
1)Перенесем слагаемые таким образом: 3/ х = х-2
2) Построим графики функций от каждой части уравнения.
Найдем координаты точек пересечения графиков данных функций.
Из построения видно, что графики функций пересекаются в точках с координатами : (3;1) и(-1;-3).
Задание. Решить уравнение: 2 х^3 – x — 1=0
Перепишем его так : 2 х 3 = x + 1
Построим графики функций от левой и правой части уравнения:
у= 2 х 3 (графиком этой функции является кубическая парабола) и график от правой части уравнения :у=х+1
Из построения видно, что абсцисса точки пересечения является х=1. значит, в ответ нужно записать: х=1
Решим графическим способом такое уравнение : х 3 =8.
Строим графики функций: у = х 3 и у=8., затем найдем абсциссу точки пересечения графиков этих функций.
Задание. Решить уравнение: √x – 0.5x = 0
Перепишем так: √x = 0.5x
Построим графики функций: у= 0.5x и у = √x
Как видно из построения, графики функций пересекаются в двух точках:
Нас интересует только координата x.
Значит уравнение √x – 0.5x = 0 имеет два корня: x 1 = 0 и x 2 = 4.
7. Решение квадратных неравенств графическим способом.
Способ , который нам хорошо известен при изучении данной темы по учебнику.
Я же предлагаю переписать неравенство следующим образом : х^2-4>3х.
Построим графики функций от левой и правой частей неравенства.
Выделим ту часть, где график от левой части выше графика от правой части.
На мой взгляд такое решение более красивое , интересное и более понятное.
8. Решение линейных неравенств и систем неравенств графическим способом.

Называют ся линейными неравенствами .
График линейного или квадратного неравенства строится так же, как строится график любой функции (уравнения).
Разница заключается в том, что неравенство подразумевает наличие множества решений, поэтому график неравенства представляет собой не просто точку на числовой прямой или линию на координатной плоскости.
С помощью математических операций и знака неравенства можно определить множество решений неравенства
Вообще графический способ решения неравенств с одной переменной применяется не только для решения квадратных неравенств, но и неравенств других видов.
Суть графического способа решения неравенств следующая:
рассматривают функции y = f(x) и y = g(x) , которые соответствуют левой и правой частям неравенства, строят их графики в одной прямоугольной системе координат и выясняют, на каких промежутках график одной из них располагается ниже или выше другого.
Те промежутки, на которых график функции у = f (х) выше графика функции y = g(х) являются решениями неравенства f(x)>g(x) ;
график функции y = f(х) не ниже графика функции y = g(x) являются решениями неравенства f(x) ≥ g(x) ;
график функции у = f (х) ниже графика функции y = g(х) являются решениями неравенства f(x) ;
график функции y = f(х) не выше графика функции y = g(х) являются решениями неравенства f(x) ≤ g(x) .
Также скажем, что абсциссы точек пересечения графиков функций y = f(x) и y = g(x) , являются решениями уравнения f(x) = g(x) .
Мы рассмотрели графический метод решения уравнений и квадратных неравенств; рассмотрели конкретные примеры, при решении которых использовали некоторые свойства функций.
Иногда при графическом решении некоторых уравнений и неравенств корни определяются только приближённо в силу того, что невозможно с высокой точностью построить график функции, измерить абсциссы или ординаты точек пересечения графика с осями координат или с другими графиками. Тем не менее, той точности, которую обеспечивает графический метод, бывает вполне достаточно для практических нужд.
Построение графиков основывается на знании основных элементарных функций, и на основные методы построения графиков функций. В работе представлено достаточное количество примеров, раскрывающих графический метод решения линейных и квадратных уравнений и неравенств, который доступен для понимания .
Работа может быть использована для углубления и расширения знаний в области построения графиков функций и использовании графического метода при решении некоторых видов уравнений и неравенств. Теорию можно использовать так же при подготовки к экзаменам , к олимпиадам.
Я свою работу представляла учащимся 8-х и 9-х классов нашей школы. И продолжаю дополнять свои исследования , а именно находить красивые решения линейных неравенств и систем неравенств.
Это и закрепление изученных свойств функций, и прекрасная демонстрация их применения на практике.
В старших классах я буду ещё знакомиться с другими функциями , с другими уравнениями и неравенствами и м не интересно будет продолжить свой проект.
http://pandia.ru/text/78/074/37096.php
http://infourok.ru/referat-reshenie-uravneniy-i-neravenstv-graficheskim-sposobom-klass-3684418.html