Реферат на тему уравнение прямой на плоскости

Если выразить в этом уравнении , то после замены и получим уравнение , называемое уравнением прямой с угловым коэффициентом, причем , где – угол между прямой и положительным направлением оси абсцисс. Если же в общем уравнении прямой перенести свободный коэффициент в правую сторону и разделить на него, то получим уравнение в отрезках

, где и – точки пересечения прямой с осями абсцисс и ординат соответственно.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Прямые называются перпендикулярными, если они пересекаются под прямым углом.

Пусть заданы две прямые и .

Чтобы найти точку пересечения прямых (если они пересекаются) необходимо решить систему с этими уравнениями. Решение этой системы и будет точкой пересечения прямых. Найдем условия взаимного расположения двух прямых.

Так как , то угол между этими прямыми находится по формуле

.

Отсюда можно получить, что при прямые будут параллельными, а при – перпендикулярны. Если прямые заданы в общем виде, то прямые параллельны при условии и перпендикулярны при условии

Расстояние от точки до прямой можно найти по формуле

Нормальное уравнение окружности:

Эллипсом называется геометрическое место точек на плоскости, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная.

Каноническое уравнение эллипса имеет вид:

где — большая полуось, — малая полуось и . Фокусы находятся в точках . Вершинами эллипса называются точки , , ,. Эксцентриситетом эллипса называется отношение

Гиперболой называется геометрическое место точек на плоскости, модуль разности расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная.

Каноническое уравнение гиперболы имеет вид:

где — большая полуось, — малая полуось и . Фокусы находятся в точках . Вершинами гиперболы называются точки , . Эксцентриситетом гиперболы называется отношение

Прямые называются асимптотами гиперболы. Если , то гипербола называется равнобочной.

Из уравнения получаем пару пересекающихся прямых и .

Параболой называется геометрическое место точек на плоскости, от каждой из которых расстояние до данной точки, называемой фокусом, равно расстоянию до данной прямой называемой директрисой, есть величина постоянная.

Каноническое уравнение параболы

.

Прямая называется директрисой, а точка – фокусом.

Понятие функциональной зависимости

Основные вопросы лекции: множества; основные операции над множествами; определение функции, ее область существования, способы задания; основные элементарные функции, их свойства и графики; числовые последовательности и их пределы; предел функции в точке и на бесконечности; бесконечно малые и бесконечно большие величины и их свойства; основные теоремы о пределах; замечательные пределы; непрерывность функции в точке и на интервале; свойства непрерывных функций.

Если каждому элементу множества ставится в соответствие вполне определенный элемент множества , то говорят что на множестве задана функция. При этом называется независимой переменной или аргументом, а – зависимой переменной, а буква обозначает закон соответствия.

Множество называется областью определения или существования функции, а множество – областью значений функции.

Существуют следующие способы задания функции

1. Аналитический способ, если функция задана формулой вида

2. Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента и соответствующие значения функции

3. Графический способ состоит в изображении графика функции – множества точек плоскости, абсциссы которых есть значения аргумента , а ординаты – соответствующие им значения функции

4. Словесный способ, если функция описывается правилом ее составления.

Основные свойства функции

1. Четность и нечетность. Функция называется четной, если для всех значений из области определения и нечетной, если . В противном случае функция называется функцией общего вида.

2. Монотонность. Функция называется возрастающей (убывающей) на промежутке , если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.

3. Ограниченность. Функция называется ограниченной на промежутке , если существует такое положительное число , что для любого . В противном случае функция называется неограниченной.

4. Периодичность. Функция называется периодической с периодом , если для любых из области определения функции .

1. Обратная функция. Пусть есть функция от независимой переменной , определенной на множестве с областью значений . Поставим в соответствие каждому единственное значение , при котором . Тогда полученная функция , определенная на множестве с областью значений называется обратной.

2. Сложная функция. Пусть функция есть функция от переменной , определенной на множестве с областью значений , а переменная в свою очередь является функцией.

Наиболее часто используются в экономике следующие функции.

1. Функция полезности и функция предпочтений – в широком смысле зависимости полезности, то есть результата, эффекта некоторого действия от уровня интенсивности этого действия.

2. Производственная функция – зависимость результата производственной деятельности от обусловивших его факторов.

3. Функция выпуска (частный вид производственной функции) – зависимость объема производства от начало или потребления ресурсов.

4. Функция издержек (частный вид производственной функции) – зависимость издержек производства от объема продукции.

5. Функции спроса, потребления и предложения – зависимость объема спроса, потребления или предложения на отдельные товары или услуги от различных факторов.

Если по некоторому закону каждому натуральному числу поставлено в соответствие вполне определенное число то говорят, что задана числовая последовательность .

:

Числа называются членами последовательности, а число — общим членом последовательности.

Число называется пределом числовой последовательности , если для любого малого числа найдется такой номер (зависящий от ), что для всех членов последовательности с номерами верно равенство .Предел числовой последовательности обозначается .

Последовательность имеющая предел называется сходящейся, в противном случае – расходящейся.

Число называется пределом функции при , если для любого малого числа найдется такое положительное число , что для всех таких, что верно неравенство .

Предел функции в точке. Пусть функция задана в некоторой окрестности точки , кроме, быть может, самой точки . Число называется пределом функции при , если для любого, даже сколь угодно малого , найдется такое положительное число (зависящий от ), что для всех и удовлетворяющих условию выполняется неравенство . Этот предел обозначается .

Функция называется бесконечно малой величиной при, если ее предел равен нулю.

Свойства бесконечно малых величин

1. Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.

2. Произведение бесконечен малой величины на ограниченную функцию есть величина бесконечно малая

3. Частное от деления бесконечно малой величины на функцию предел которой отличен от нуля, есть величина бесконечно малая.

Понятие производной и дифференциала функции

Основные вопросы лекции: задачи, приводящие к понятию производной; определение производной; геометрический и физический смысл производной; понятие дифференцируемой функции; основные правила дифференцирования; производные основных элементарных функций; производная сложной и обратной функции; производные высших порядков, основные теоремы дифференциального исчисления; теорема Лопиталя; раскрытие неопределенностей; возрастание и убывание функции; экстремум функции; выпуклость и вогнутость графика функции; аналитические признаки выпуклости и вогнутости; точки перегиба; вертикальные и наклонные асимптоты графика функции; общая схема исследования функции и построение ее графика, определение функции нескольких переменных; предел и непрерывность; частные производные и дифференциал функции; производная по направлению, градиент; экстремум функции нескольких переменных; наибольшее и наименьшее значения функции; условный экстремум, метод Лагранжа.

Производной функции называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует)

.

Если функция в точке имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция дифференцируемая в каждой точке промежутка , называется дифференцируемой на этом промежутке.

Геометрический смысл производной: производная есть угловой коэффициент (тангенс угла наклона) касательной, приведенной к кривой в точке .

Тогда уравнение касательной к кривой в точке примет вид

.

Механический смысл производной: производная пути по времени есть скорость точки в момент времени :

Экономический смысл производной: производная объема произведенной продукции по времени есть производительность труда в момент

Теорема. Если функция дифференцируема в точке , то она в этой точке непрерывна.

Производная функции может быть найдена по следующей схеме

1. Дадим аргументу приращение и найдем наращенное значение функции .

2. Находим приращение функции .

3. Составляем отношение .

4. Находим предел этого отношения при, то есть (если этот предел существует).

1. Производная постоянной равна нулю, то есть.

2. Производная аргумента равна 1, то есть .

3. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, то есть .

4. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, то есть

5. Производная частного двух дифференцируемых функций может быть найдена по формуле:

.

Теорема. Если и – дифференцируемые функции от своих переменных, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменной , то есть

.

Теорема. Для дифференцируемой функции с производной не равной нулю, производная обратной функции равна обратной величине производной данной функции, то есть .

Эластичностью функции называется предел отношения относительного приращения функции к относительному приращению переменной при:

Эластичность функции показывает приближенно, на сколько процентов изменится функция при изменении независимой переменной на один процент.

Геометрически это означает что эластичность функции (по абсолютной величине) равна отношению расстояний по касательной от данной точки графика функции до точек ее пересечения с осями и .

Основные свойства эластичности функции:

1. Эластичность функции равна произведению независимой переменной на темп изменения функции , то есть .

2. Эластичность произведения (частного) двух функций равна сумме (разности) эластичностей этих функций:

, .

3. Эластичность взаимообратных функций – взаимно обратные величины:

Эластичность функции применяется при анализе спроса и потребления.

Теорема Ферма. Если дифференцируемая на промежутке функция достигает наибольшего или наименьшего значения во внутренней точке этого промежутка, то производная функции в этой точке равна нулю, то есть .

Теорема Ролля. Пусть функция удовлетворяет следующим условиям:

1) непрерывна на отрезке ;

2) дифференцируема на интервале ;

3) на концах отрезка принимает равные значения, то есть .

Тогда внутри отрезка существует по крайней мере одна такая точка , в которой производная функции равна нулю: .

Теорема Лагранжа. Пусть функция удовлетворяет следующим условиям

1. Непрерывна на отрезке .

2. Дифференцируема на интервале ;

Тогда внутри отрезка существует по крайней мере одна такая точка , в которой производная равна частному от деления приращения функции на приращение аргумента на этом отрезке, то есть .

Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле. Итак, если имеется неопределенность вида или , то

Теорема (достаточное условие возрастания функции)

Если производная дифференцируемой функции положительна внутри некоторого промежутка Х, то она возрастаетна этом промежутке.

Теорема (достаточное условие убывания функции), Если производная дифференцируемой функции отрицательна внутри некоторого промежутка, то она убывает на этом промежутке.

Точка называется точкой максимума функции , если в некоторой окрестности точки выполняется неравенство .

Точка называется точкой минимума функции , если в некоторой окрестности точки выполняется неравенство .

Значения функции в точках и называются соответственно максимумом и минимумом функции. Максимум и минимум функции объединяются общим названием экстремума функции.

Для того, чтобы функция имела экстремум в точке необходимо, чтобы ее производная в этой точке равнялась нулю или не существовала.

Первое достаточное условие экстремума. Теорема.

Если при переходе через точку производная дифференцируемой функции меняет свой знак с плюса на минус, то точка есть точка максимума функции , а если с минуса на плюс, – то точка минимума.

Схема исследования функции на экстремум.

1. Найти производную .

2. Найти критические точки функции, в которых производная или не существует.

3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.

4. Найти экстремумы (экстремальные значения) функции.

Второе достаточное условие экстремума. Теорема.

Если первая производная дважды дифференцируемой функции равна нулю в некоторой точке , а вторая производная в этой точке положительна, то есть точка минимума функции , если отрицательна, то – точка максимума.

Для отыскания наибольшего и наименьшего значений на отрезке пользуемся следующей схемой.

1. Найти производную .

2. Найти критические точки функции, в которых или не существует.

3. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее и наименьшее .

Функция называется выпуклой вверх на промежутке Х, если отрезок соединяющий любые две точки графика лежит под графиком функции.

Функция называется выпуклой вниз на промежутке Х, если отрезок соединяющий любые две точки графика лежит над графиком функции.

Теорема. Функция выпукла вниз (вверх) на промежутке Х тогда и только тогда, когда ее первая производная на этом промежутке монотонно возрастает (убывает).

Теорема. Если вторая производная дважды дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка Х, то функция выпукла вниз (вверх) на этом промежутке.

Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вниз и вверх.

Теорема (необходимое условие перегиба). Вторая производная дважды дифференцируемой функции в точке перегиба равна нулю, то есть .

Теорема (достаточное условие перегиба). Если вторая производная дважды дифференцируемой функции при переходе через некоторую точку меняет свой знак, то есть точка перегиба ее графика.

Схема исследования функции на выпуклость и точки перегиба:

1. Найти вторую производную функции .

2. Найти точки, в которых второй производная или не существует.

3. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба.

4. Найти значения функции в точках перегиба.

При исследовании функции на построение их графиков рекомендуется использовать следующую схему:

1. Найти область определения функции.

2. Исследовать функцию на четность – нечетность.

3. Найти вертикальные асимптоты

4. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.

5. Найти экстремумы и интервалы монотонности функции.

6. Найти интервалы выпуклости функции и точки перегиба.

7. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.

Дифференциалом функции называется главная, линейная относительно часть приращения функции, равная произведению производной на приращении независимой переменной.

Пусть имеется переменных величин, и каждому набору их значений из некоторого множества Х соответствует одно вполне определенное значение переменной величины . Тогда говорят, что задана функция нескольких переменных .

Переменные называются независимыми переменными или аргументами, — зависимой переменной. Множество Х называется областью определения функции.

Многомерным аналогом функции полезности является функция , выражающая зависимость от приобретенных товаров.

Также на случай переменных обобщается понятие производственной функции, выражающей результат производственной деятельности от обусловивших его факторов .

Функцию двух переменных будем обозначать . Ее область определения есть подмножество координатной плоскости. Окрестностью точки называется круг, содержащий точку .

Число называется пределом функции при и (или в точке ), если для любого малого числа найдется число (зависящее от ), такое, что для всех точек , отстоящих от точек на расстояние меньшее, чем , выполняется неравенство .

Обозначается предел так; .

Функция называется непрерывной в точке , если она

1. определена в точке

2. имеет конечный предел при и

3. этот предел равен значению функции в точке, то есть .

Величина называется полным приращением функции в точке . Если задать приращение только одной какой-либо переменной то получается частное приращение. Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю (если этот предел существует). Таким образом, для функции по определению

.

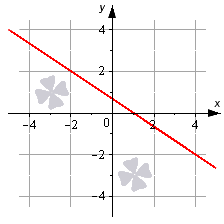
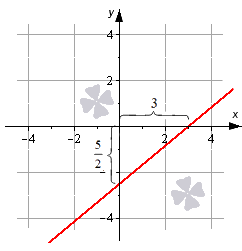
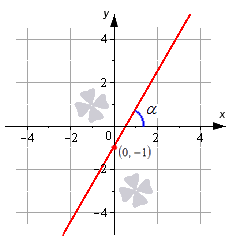
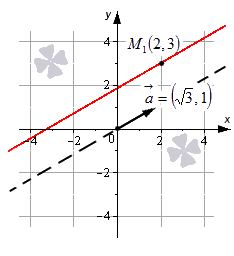
Дифференциалом функции называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, то есть

или .

Функция называется дифференцируемой в точке , если ее полное приращение может быть представлено в виде , где

– бесконечно малые при.

Теорема. Если частные производные и функции существуют в окрестности точки и непрерывны в самой точке , то функция дифференцируема в этой точке.

Градиентом функции называется вектор . Градиент функции в данной точке характеризует направление максимальной скорости изменения функции в этой точке.

Точка называется точкой максимума (минимума) функции , если существует окрестность точки , такая, что для всех точек из этой окрестности выполняется неравенство

Теорема. Пусть точка – есть точка экстремума дифференцируемой функции . Тогда частные производные и в этой точке равны нулю.

Равенство частных производных нулю выражает лишь необходимое, но недостаточное условие экстремума функции нескольких переменных.

Если частные производные и сами являются дифференцируемыми функциями, то можно определить также и их частные производные, которые называются частными производными второго порядка.

Если частные производные второго порядка функции непрерывны в точке , то в этой точке .

Теорема (достаточное условие экстремума функции двух переменных). Пусть функция

1. определена в некоторой окрестности критической точки , в которой .

2. имеет в этой точке непрерывные частные производные второго порядка , , .

Тогда, если , то в точке функция имеет экстремум, причем если – максимум, если – минимум. В случае функция экстремумов не имеет. Если , то вопрос о наличии экстремума остается открытым.

Исследование функции двух переменных на экстремум рекомендуется проводить по следующей схеме:

1. Найти частные производные первого порядка.

2. Решить систему уравнений , и найти критические точки функции.

3. Найти частные производные второго порядка, вычислить их значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.

Найти экстремумы (экстремальные значения) функции.

1. Высшая математика для экономистов: Учебник для вузов / Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2003.

2.Е.С. Кочетков, С.О. Смерчинская Теория вероятностей в задачах и упражнениях / М. ИНФРА-М 2005.

3. Высшая математика для экономистов: Практикум / Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2004. Ч. 1, 2

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., Высшая школа, 1977

5. Гмурман В.Е. Теория вероятностей и математическая статистика. М., Высшая школа, 1977

6. М.С. Красс Математика для экономических специальностей: Учебник/ М. ИНФРА-М 1998.

7. Выгодский М.Я. Справочник по высшей математике. – М., 2000.

8.Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1971.

9.А.К. Казашев Сборник задач по высшей математике для экономистов – Алматы — 2002 г.

10.Пискунов Н.С. Дифференциальное и интегральное исчисление. – М.: Наука, 1985, Т. 1,2.

11.П.Е. Данко, А.Г. Попов, Т.Я. Кожевников Высшая математика в упражнениях и задачах/ М. ОНИКС-2005.

12.И.А. Зайцев Высшая математика/ М. Высшая школа-1991 г.

13.Головина Л.И. Линейная алгебра и некоторые ее приложения. – М.: Наука, 1985.

14.Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы анализа экономики. – М.: ДИС, 1997.

15.Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. – М.: Высшая школа, 1982 – Ч 1, 2.

16.Колесников А.Н. Краткий курс математики для экономистов. – М.: Инфра-М, 1997.

17.В.С. Шипацев Задачник по высшей математике-М. Высшая школа, 2005 г.

Уравнение прямой, виды уравнения прямой на плоскости

В прошлом материале мы рассмотрели основные моменты, касающиеся темы прямой на плоскости. Теперь же перейдем к изучению уравнения прямой: рассмотрим, какое уравнение может называться уравнением прямой, а также то, какой вид имеет уравнение прямой на плоскости.

Определение уравнения прямой на плоскости

Допустим, что есть прямая линия, которая задана в прямоугольной декартовой системе координат O х у .

Прямая линия – это геометрическая фигура, которая состоит из точек. Каждая точка имеет свои координаты по осям абсцисс и ординат. Уравнение, которое описывает зависимость координат каждой точки прямой в декартовой системе O x y , называется уравнением прямой на плоскости.

Фактически, уравнение прямой на плоскости – это уравнение с двумя переменными, которые обозначаются как x и y . Уравнение обращается в тождество при подстановке в него значений любой из точек прямой линии.

Давайте посмотрим, какой вид будет иметь уравнение прямой на плоскости. Этому будет посвящен весь следующий раздел нашей статьи. Отметим, что существует несколько вариантов записи уравнения прямой. Объясняется это наличием нескольких способов задания прямой линии на плоскости, и также различной спецификой задач.

Общее уравнение прямой линии

Познакомимся с теоремой, которая задает вид уравнения прямой линии на плоскости в декартовой системе координат O x y .

Уравнение вида A x + B y + C = 0 , где x и y – переменные, а А , В и C – это некоторые действительные числа, из которых A и B не равны нулю, задает прямую линию в декартовой системе координат O x y . В свою очередь, любая прямая линия на плоскости может быть задана уравнением вида A x + B y + C = 0 .

Таким образом, общее уравнение прямой на плоскости имеет вид A x + B y + C = 0 .

Поясним некоторые важные аспекты темы.

Посмотрите на рисунок.

Линия на чертеже определяется уравнением вида 2 x + 3 y — 2 = 0 , так как координаты любой точки, составляющей эту прямую, удовлетворяют приведенному уравнению. В то же время, определенное количество точек плоскости, определяемых уравнением 2 x + 3 y — 2 = 0 , дают нам прямую линию, которую мы видим на рисунке.

Общее уравнение прямой может быть полным и неполным. В полном уравнении все числа А , В и C отличны от нуля. Во всех остальных случаях уравнение считается неполным. Уравнение вида A x + B y = 0 определяет прямую линию, которая проходит через начало координат. Если A равно нулю, то уравнение A x + B y + C = 0 задает прямую, расположенную параллельно оси абсцисс O x . Если B равно нулю, то линия параллельна оси ординат O y .

Вывод: при некотором наборе значений чисел А , В и C с помощью общего уравнения прямой можно записать любую прямую линию на плоскости в прямоугольной системе координат O х у .

Прямая, заданная уравнением вида A x + B y + C = 0 , имеет нормальный вектор прямой с координатами A , B .

Все приведенные уравнения прямых, которые мы рассмотрим ниже, могут быть получены из общего уравнения прямой. Также возможен и обратный процесс, когда любое из рассматриваемых уравнений может быть приведено к общему уравнению прямой.

Разобраться во всех нюансах темы можно в статье «Общее уравнение прямой». В материале мы приводим доказательство теоремы с графическими иллюстрациями и подробным разбором примеров. Особое внимание в статье уделяется переходам от общего уравнения прямой к уравнениям других видов и обратно.

Уравнение прямой в отрезках

Уравнение прямой в отрезках имеет вид x a + y b = 1 , где a и b – это некоторые действительные числа, которые не равны нулю. Абсолютные величины чисел a и b равны длине отрезков, которые отсекаются прямой линией на осях координат. Длина отрезков отсчитывается от начала координат.

Благодаря уравнению можно легко построить прямую линию на чертеже. Для этого необходимо отметить в прямоугольной системе координат точки a , 0 и 0 , b , а затем соединить их прямой линией.

Построим прямую, которая задана формулой x 3 + y — 5 2 = 1 . Отмечаем на графике две точки 3 , 0 , 0 , — 5 2 , соединяем их между собой.

Дополнительно рекомендуем ознакомиться с материалом, изложенным в статье «Уравнение прямой в отрезках».

Уравнение прямой с угловым коэффициентом

Эти уравнения, имеющие вид y = k · x + b должны быть нам хорошо известны из курса алгебры. Здесь x и y – это переменные, k и b – это некоторые действительные числа, из которых k представляет собой угловой коэффициент. В этих уравнениях переменная у является функцией аргумента x .

Дадим определение углового коэффициента через определение угла наклона прямой к положительному направлению оси O x .

Для обозначения угла наклона прямой к положительному направлению оси O x в декартовой системе координат введем величину угла α . Угол отсчитывается от положительного направления оси абсцисс до прямой линии против хода часовой стрелки. Угол α считается равным нулю в том случае, если линия параллельна оси O x или совпадает с ней.

Угловой коэффициент прямой – это тангенс угла наклона этой прямой. Записывается это следующим образом k = t g α . Для прямой, которая располагается параллельно оси O y или совпадает с ней, записать уравнение прямой с угловым коэффициентом не представляется возможным, так как угловой коэффициент в этом случае превращается в бесконечность (не существует).

Прямая, которая задана уравнением y = k · x + b , проходит через точку 0 , b на оси ординат. Это значит, что уравнение прямой с угловым коэффициентом y = k · x + b , задает на плоскости прямую линию, которая проходит через точку 0 , b и образует угол α с положительным направлением оси O x , причем k = t g α .

Изобразим прямую линию, которая определяется уравнением вида y = 3 · x — 1 .

Эта линия должна пройти через точку ( 0 , — 1 ) . Угол наклона α = a r c t g 3 = π 3 равен 60 градусов к положительному направлению оси O x . Угловой коэффициент равен 3

Обращаем ваше внимание, что с помощью уравнения прямой с угловым коэффициентом очень удобно искать уравнение касательной к графику функции в точке.

Больше материала по теме можно найти в статье «Уравнение прямой с угловым коэффициентом». Помимо теории там размещено большое количество графических примеров и подробный разбор задач.

Каноническое уравнение прямой на плоскости

Данный вид уравнения имеет вид x — x 1 a x = y — y 1 a y , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не равны нулю.

Прямая линия, заданная каноническим уравнением прямой, проходит через точку M 1 ( x 1 , y 1 ) . Числа a x и a y в знаменателях дробей представляют собой координаты направляющего вектора прямой линии. Это значит, что каноническое уравнение прямой линии x — x 1 a x = y — y 1 a y в декартовой системе координат O x y соответствует линии, проходящей через точку M 1 ( x 1 , y 1 ) и имеющей направляющий вектор a → = ( a x , a y ) .

Изобразим в системе координат O x y прямую линию, которая задается уравнением x — 2 3 = y — 3 1 . Точка M 1 ( 2 , 3 ) принадлежит прямой, вектор a → ( 3 , 1 ) является направляющим вектором этой прямой линии.

Каноническое уравнение прямой линии вида x — x 1 a x = y — y 1 a y может быть использовано в случаях, когда a x или a y равно нулю. Наличие ноля в знаменателе делает запись x — x 1 a x = y — y 1 a y условной. Уравнение можно записать следующим образом a y ( x — x 1 ) = a x ( y — y 1 ) .

В том случае, когда a x = 0 , каноническое уравнение прямой принимает вид x — x 1 0 = y — y 1 a y и задает прямую линию, которая расположена параллельно оси ординат или совпадает с этой осью.

Каноническое уравнение прямой при условии, что a y = 0 , принимает вид x — x 1 a x = y — y 1 0 . Такое уравнение задает прямую линию, расположенную параллельно оси абсцисс или совпадающую с ней.

Больше материала на тему канонического уравнения прямой смотрите здесь. В статье мы приводим целый ряд решений задач, а также многочисленные примеры, которые позволяют лучше овладеть темой.

Параметрические уравнения прямой на плоскости

Данные уравнения имеют вид x = x 1 + a x · λ y = y 1 + a y · λ , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не могут быть одновременно равны нулю. В формулу вводится дополнительный параметр λ , который может принимать любые действительные значения.

Назначение параметрического уравнения в том, чтобы установить неявную зависимости между координатами точек прямой линии. Для этого и вводится параметр λ .

Числа x , y представляют собой координаты некоторой точки прямой. Они вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра λ .

Предположим, что λ = 0 .

Тогда x = x 1 + a x · 0 y = y 1 + a y · 0 ⇔ x = x 1 y = y 1 , т. е. точка с координатами ( x 1 , y 1 ) принадлежит прямой.

Обращаем ваше внимание на то, что коэффициенты a x и a y при параметре λ в данном виде уравнений представляют собой координаты направляющего вектора прямой линии.

Рассмотрим параметрические уравнения прямой линии вида x = 2 + 3 · λ y = 3 + λ . Прямая, заданная уравнениями, в декартовой системе координат проходит через точку ( x 1 , y 1 ) и имеет направляющий вектор a → = ( 3 , 1 ) .

Больше информации ищите в статье «Параметрические уравнения прямой на плоскости».

Нормальное уравнение прямой

Нормальное уравнение прямой имеет вид , A x + B y + C = 0 , где числа А , В , и C таковы, что длина вектора n → = ( A , B ) равна единице, а C ≤ 0 .

Нормальным вектором линии, заданной нормальным уравнением прямой в прямоугольной системе координат O х у , является вектор n → = ( A , B ) . Эта прямая проходит на расстоянии C от начала координат в направлении вектора n → = ( A , B ) .

Еще одним вариантом записи нормального уравнения прямой линии является cos α · x + cos β · y — p = 0 , где cos α и cos β — это два действительных числа, которые представляют собой направляющие косинусы нормального вектора прямой единичной длины. Это значит, что n → = ( cos α , cos β ) , справедливо равенство n → = cos 2 α + cos 2 β = 1 , величина p ≥ 0 и равна расстоянию от начала координат до прямой.

Рассмотрим общее уравнение прямой — 1 2 · x + 3 2 · y — 3 = 0 . Это общее уравнение прямой является нормальным уравнением прямой, так как n → = A 2 + B 2 = — 1 2 2 + 3 2 = 1 и C = — 3 ≤ 0 .

Уравнение задает в декартовой системе координат 0ху прямую линию, нормальный вектор которой имеет координаты — 1 2 , 3 2 . Линия удалена от начала координат на 3 единицы в направлении нормального вектора n → = — 1 2 , 3 2 .

Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.

Если в общем уравнении прямой A x + B y + C = 0 числа А , В и С таковы, что уравнение A x + B y + C = 0 не является нормальным уравнением прямой, то его можно привести к нормальному виду. Подробнее об этом читайте в статье «Нормальное уравнение прямой».