Реферат на тему уравнение прямой в плоскости

Уравнение прямой, виды уравнения прямой на плоскости

В прошлом материале мы рассмотрели основные моменты, касающиеся темы прямой на плоскости. Теперь же перейдем к изучению уравнения прямой: рассмотрим, какое уравнение может называться уравнением прямой, а также то, какой вид имеет уравнение прямой на плоскости.

Определение уравнения прямой на плоскости

Допустим, что есть прямая линия, которая задана в прямоугольной декартовой системе координат O х у .

Прямая линия – это геометрическая фигура, которая состоит из точек. Каждая точка имеет свои координаты по осям абсцисс и ординат. Уравнение, которое описывает зависимость координат каждой точки прямой в декартовой системе O x y , называется уравнением прямой на плоскости.

Фактически, уравнение прямой на плоскости – это уравнение с двумя переменными, которые обозначаются как x и y . Уравнение обращается в тождество при подстановке в него значений любой из точек прямой линии.

Давайте посмотрим, какой вид будет иметь уравнение прямой на плоскости. Этому будет посвящен весь следующий раздел нашей статьи. Отметим, что существует несколько вариантов записи уравнения прямой. Объясняется это наличием нескольких способов задания прямой линии на плоскости, и также различной спецификой задач.

Общее уравнение прямой линии

Познакомимся с теоремой, которая задает вид уравнения прямой линии на плоскости в декартовой системе координат O x y .

Уравнение вида A x + B y + C = 0 , где x и y – переменные, а А , В и C – это некоторые действительные числа, из которых A и B не равны нулю, задает прямую линию в декартовой системе координат O x y . В свою очередь, любая прямая линия на плоскости может быть задана уравнением вида A x + B y + C = 0 .

Таким образом, общее уравнение прямой на плоскости имеет вид A x + B y + C = 0 .

Поясним некоторые важные аспекты темы.

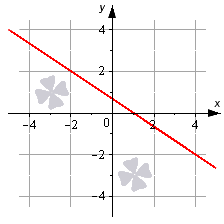
Посмотрите на рисунок.

Линия на чертеже определяется уравнением вида 2 x + 3 y — 2 = 0 , так как координаты любой точки, составляющей эту прямую, удовлетворяют приведенному уравнению. В то же время, определенное количество точек плоскости, определяемых уравнением 2 x + 3 y — 2 = 0 , дают нам прямую линию, которую мы видим на рисунке.

Общее уравнение прямой может быть полным и неполным. В полном уравнении все числа А , В и C отличны от нуля. Во всех остальных случаях уравнение считается неполным. Уравнение вида A x + B y = 0 определяет прямую линию, которая проходит через начало координат. Если A равно нулю, то уравнение A x + B y + C = 0 задает прямую, расположенную параллельно оси абсцисс O x . Если B равно нулю, то линия параллельна оси ординат O y .

Вывод: при некотором наборе значений чисел А , В и C с помощью общего уравнения прямой можно записать любую прямую линию на плоскости в прямоугольной системе координат O х у .

Прямая, заданная уравнением вида A x + B y + C = 0 , имеет нормальный вектор прямой с координатами A , B .

Все приведенные уравнения прямых, которые мы рассмотрим ниже, могут быть получены из общего уравнения прямой. Также возможен и обратный процесс, когда любое из рассматриваемых уравнений может быть приведено к общему уравнению прямой.

Разобраться во всех нюансах темы можно в статье «Общее уравнение прямой». В материале мы приводим доказательство теоремы с графическими иллюстрациями и подробным разбором примеров. Особое внимание в статье уделяется переходам от общего уравнения прямой к уравнениям других видов и обратно.

Уравнение прямой в отрезках

Уравнение прямой в отрезках имеет вид x a + y b = 1 , где a и b – это некоторые действительные числа, которые не равны нулю. Абсолютные величины чисел a и b равны длине отрезков, которые отсекаются прямой линией на осях координат. Длина отрезков отсчитывается от начала координат.

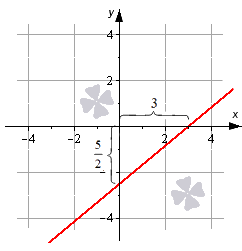
Благодаря уравнению можно легко построить прямую линию на чертеже. Для этого необходимо отметить в прямоугольной системе координат точки a , 0 и 0 , b , а затем соединить их прямой линией.

Построим прямую, которая задана формулой x 3 + y — 5 2 = 1 . Отмечаем на графике две точки 3 , 0 , 0 , — 5 2 , соединяем их между собой.

Дополнительно рекомендуем ознакомиться с материалом, изложенным в статье «Уравнение прямой в отрезках».

Уравнение прямой с угловым коэффициентом

Эти уравнения, имеющие вид y = k · x + b должны быть нам хорошо известны из курса алгебры. Здесь x и y – это переменные, k и b – это некоторые действительные числа, из которых k представляет собой угловой коэффициент. В этих уравнениях переменная у является функцией аргумента x .

Дадим определение углового коэффициента через определение угла наклона прямой к положительному направлению оси O x .

Для обозначения угла наклона прямой к положительному направлению оси O x в декартовой системе координат введем величину угла α . Угол отсчитывается от положительного направления оси абсцисс до прямой линии против хода часовой стрелки. Угол α считается равным нулю в том случае, если линия параллельна оси O x или совпадает с ней.

Угловой коэффициент прямой – это тангенс угла наклона этой прямой. Записывается это следующим образом k = t g α . Для прямой, которая располагается параллельно оси O y или совпадает с ней, записать уравнение прямой с угловым коэффициентом не представляется возможным, так как угловой коэффициент в этом случае превращается в бесконечность (не существует).

Прямая, которая задана уравнением y = k · x + b , проходит через точку 0 , b на оси ординат. Это значит, что уравнение прямой с угловым коэффициентом y = k · x + b , задает на плоскости прямую линию, которая проходит через точку 0 , b и образует угол α с положительным направлением оси O x , причем k = t g α .

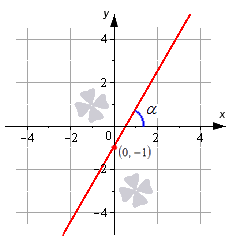
Изобразим прямую линию, которая определяется уравнением вида y = 3 · x — 1 .

Эта линия должна пройти через точку ( 0 , — 1 ) . Угол наклона α = a r c t g 3 = π 3 равен 60 градусов к положительному направлению оси O x . Угловой коэффициент равен 3

Обращаем ваше внимание, что с помощью уравнения прямой с угловым коэффициентом очень удобно искать уравнение касательной к графику функции в точке.

Больше материала по теме можно найти в статье «Уравнение прямой с угловым коэффициентом». Помимо теории там размещено большое количество графических примеров и подробный разбор задач.

Каноническое уравнение прямой на плоскости

Данный вид уравнения имеет вид x — x 1 a x = y — y 1 a y , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не равны нулю.

Прямая линия, заданная каноническим уравнением прямой, проходит через точку M 1 ( x 1 , y 1 ) . Числа a x и a y в знаменателях дробей представляют собой координаты направляющего вектора прямой линии. Это значит, что каноническое уравнение прямой линии x — x 1 a x = y — y 1 a y в декартовой системе координат O x y соответствует линии, проходящей через точку M 1 ( x 1 , y 1 ) и имеющей направляющий вектор a → = ( a x , a y ) .

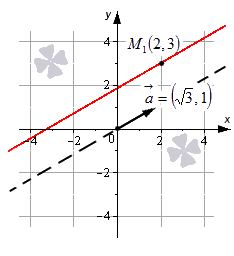
Изобразим в системе координат O x y прямую линию, которая задается уравнением x — 2 3 = y — 3 1 . Точка M 1 ( 2 , 3 ) принадлежит прямой, вектор a → ( 3 , 1 ) является направляющим вектором этой прямой линии.

Каноническое уравнение прямой линии вида x — x 1 a x = y — y 1 a y может быть использовано в случаях, когда a x или a y равно нулю. Наличие ноля в знаменателе делает запись x — x 1 a x = y — y 1 a y условной. Уравнение можно записать следующим образом a y ( x — x 1 ) = a x ( y — y 1 ) .

В том случае, когда a x = 0 , каноническое уравнение прямой принимает вид x — x 1 0 = y — y 1 a y и задает прямую линию, которая расположена параллельно оси ординат или совпадает с этой осью.

Каноническое уравнение прямой при условии, что a y = 0 , принимает вид x — x 1 a x = y — y 1 0 . Такое уравнение задает прямую линию, расположенную параллельно оси абсцисс или совпадающую с ней.

Больше материала на тему канонического уравнения прямой смотрите здесь. В статье мы приводим целый ряд решений задач, а также многочисленные примеры, которые позволяют лучше овладеть темой.

Параметрические уравнения прямой на плоскости

Данные уравнения имеют вид x = x 1 + a x · λ y = y 1 + a y · λ , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не могут быть одновременно равны нулю. В формулу вводится дополнительный параметр λ , который может принимать любые действительные значения.

Назначение параметрического уравнения в том, чтобы установить неявную зависимости между координатами точек прямой линии. Для этого и вводится параметр λ .

Числа x , y представляют собой координаты некоторой точки прямой. Они вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра λ .

Предположим, что λ = 0 .

Тогда x = x 1 + a x · 0 y = y 1 + a y · 0 ⇔ x = x 1 y = y 1 , т. е. точка с координатами ( x 1 , y 1 ) принадлежит прямой.

Обращаем ваше внимание на то, что коэффициенты a x и a y при параметре λ в данном виде уравнений представляют собой координаты направляющего вектора прямой линии.

Рассмотрим параметрические уравнения прямой линии вида x = 2 + 3 · λ y = 3 + λ . Прямая, заданная уравнениями, в декартовой системе координат проходит через точку ( x 1 , y 1 ) и имеет направляющий вектор a → = ( 3 , 1 ) .

Больше информации ищите в статье «Параметрические уравнения прямой на плоскости».

Нормальное уравнение прямой

Нормальное уравнение прямой имеет вид , A x + B y + C = 0 , где числа А , В , и C таковы, что длина вектора n → = ( A , B ) равна единице, а C ≤ 0 .

Нормальным вектором линии, заданной нормальным уравнением прямой в прямоугольной системе координат O х у , является вектор n → = ( A , B ) . Эта прямая проходит на расстоянии C от начала координат в направлении вектора n → = ( A , B ) .

Еще одним вариантом записи нормального уравнения прямой линии является cos α · x + cos β · y — p = 0 , где cos α и cos β — это два действительных числа, которые представляют собой направляющие косинусы нормального вектора прямой единичной длины. Это значит, что n → = ( cos α , cos β ) , справедливо равенство n → = cos 2 α + cos 2 β = 1 , величина p ≥ 0 и равна расстоянию от начала координат до прямой.

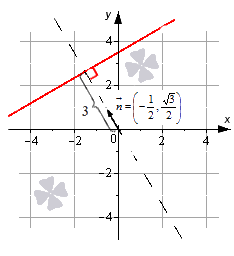
Рассмотрим общее уравнение прямой — 1 2 · x + 3 2 · y — 3 = 0 . Это общее уравнение прямой является нормальным уравнением прямой, так как n → = A 2 + B 2 = — 1 2 2 + 3 2 = 1 и C = — 3 ≤ 0 .

Уравнение задает в декартовой системе координат 0ху прямую линию, нормальный вектор которой имеет координаты — 1 2 , 3 2 . Линия удалена от начала координат на 3 единицы в направлении нормального вектора n → = — 1 2 , 3 2 .

Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.

Если в общем уравнении прямой A x + B y + C = 0 числа А , В и С таковы, что уравнение A x + B y + C = 0 не является нормальным уравнением прямой, то его можно привести к нормальному виду. Подробнее об этом читайте в статье «Нормальное уравнение прямой».

Реферат «Плоскости в пространстве»

Скачать:

Предварительный просмотр:

Муниципальное образовательное учреждение

Маклинская средняя полная общеобразовательная школа

с углубленным изучением отдельных предметов

«Плоскости в пространстве»

Автор: ученик 11А класса

Соколова Татьяна Владимировна

1. Введение 3
2. Способы задания плоскости 4
3. Взаимное расположение плоскостей в пространстве 7
4. Параллельность плоскостей 8

1. Признаки параллельности плоскостей 8
2. Свойства параллельных плоскостей 10

1. Двугранные углы и угол между двумя плоскостями 14

1. Двугранный угол и его измерение 14
2. Угол между двумя плоскостями 17

1. Перпендикулярность плоскостей 19

6.1. Признаки перпендикулярности двух плоскостей 19

6.2. Свойства перпендикулярных плоскостей 20

7. Заключение 24

8. Список используемой литературы 25

Из курса планиметрии мы знаем, что плоскость – это множество, элементами которого являются точки и в котором выполняется система аксиом планиметрии, описывающая свойства точек и прямы.

Пространство – это множество, элементами которого являются точки и в котором выполняется система аксиом стереометрии, описывающая свойства точек, прямых и плоскостей.

Система аксиом стереометрии дает описание свойств пространства и основных его элементов. Понятия «точка», «прямая» и «плоскость» принимаются без определений: их описание и свойства содержатся в аксиомах. С другой стороны, понятия «точка», «прямая», «плоскость» имеют наглядный смысл, отраженный на чертежах и рисунках.

Изучение пространства приводит к необходимости расширить систему аксиом планиметрии и рассмотреть новую группу аксиом, в которых выражены свойства взаимного расположения точек, прямых и плоскостей, что особенно важно для нас, в пространстве.

Цель реферата – получить наглядное представление о пространстве и способах расположения плоскостей в пространстве.

Для выполнения этой цели поставлены следующие задачи:

— рассмотреть способы задания плоскостей в пространстве,

— рассмотреть основные аксиомы стереометрии;

— изучить возможные варианты взаимного расположения плоскостей в пространстве,

— сформулировать основные признаки и свойства взаимного расположения плоскостей в пространстве;

— проиллюстрировать теоретический материал практическими примерами.

2. Способы задания плоскости

Изучение пространства приводит к необходимости расширить систему аксиом.

Рассмотрим аксиому R1 . В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии. Эта аксиома дает нам право рассматривать в любой плоскости пространства отрезки, прямые со всеми их свойствами, которые изучались в планиметрии. Например, если прямая а и не принадлежащая ей точка М лежат в некоторой плоскости α, то в этой плоскости можно провести через точку М прямую, параллельную прямой а , и притом только одну.

В аксиоме R3 говорится: какова бы не была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей. Данной аксиомой утверждается, что для любой плоскости в пространстве можно выбрать любое количество точек в этой плоскости, равно как и сколько угодно точек вне её. В случае, если точка А лежит в (принадлежит) плоскости α, то записывают: А α и говорят, что плоскость α проходит через точку А . Если точка А не принадлежит плоскости α, то записывают : А α и говорят, что плоскость α не проходит через точку А.

Плоскость в пространстве однозначно определяется:

— тремя точками, не лежащими на прямой. Аксиома R2 (аксиома плоскости) гласит: Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну. Плоскость, которая проходит через точки А, В и С , не принадлежащие одной прямой (С АВ) , обозначается символически (АВС) ; если этой плоскостью является плоскость α, то пишут α = (АВС) или (АВС)= α. Стол, имеющий три ножки, не может качаться на плоском полу. Его устойчивость объясняется тем, что концы трех его ножек (три точки) принадлежат одной плоскости – плоскости пола, но не принадлежат одной прямой. Плохо сделанный стол на четырех ножках качается на плоском полу, и под одну из его ножек что-нибудь стараются подложить.

— прямой и точкой, не лежащей на прямой.

По теореме 1 через любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну.

Доказательство. Пусть даны прямая а и не принадлежащая ей точка А. Выберем на прямой а любые точки В и С . Через точки В и С проходит только одна прямая – прямая а . Так как точка А по условию теоремы не принадлежит прямой а , то точки А, В и С не принадлежат одной прямой. По аксиоме R2 через точки А,В,С проходит только одна плоскость – плоскость АВС , которую обозначим α . Прямая а имеет с ней две общие точки – точки В и С , следовательно по аксиоме R4 (аксиоме прямой и плоскости — Если прямая проходит через две точки плоскости, то она лежит в этой плоскости ) эта прямая лежит в плоскости α . Таким образом, плоскость α проходит через прямую а и точку А и является искомой.

Докажем, что другой плоскости, проходящей через прямую а и точку А а , не существует.

Предположим, что есть другая плоскость – α , проходящая через точку А и прямую а . Тогда плоскости α и α проходят через точки А, В и С, не принадлежащие одной прямой, а значит совпадают. Следовательно, плоскость α единственная. Теорема доказана.

— двумя пересекающимися прямыми.

Две прямые в пространстве называются пересекающимися, если они имеют ровно одну общую точку.

Теорема 2. Через любые две пересекающиеся прямые можно провести плоскость, и притом только одну.

Доказательство. Пусть данные прямые а и b пересекаются в точке С . Выберем на прямых а и b любые точки А и В , отличные от С : А а, В b. Тогда точки А, В и С не принадлежат одной прямой, и по аксиоме R2 через них можно провести только одну плоскость. Обозначим её α .

Точки А и С прямой а принадлежат плоскости α , значит, плоскость α проходит через прямую а ( аксиома R4: Если прямая проходит через две точки плоскости, то она лежит в этой плоскости) . Плоскость α проходит и через прямую b , так как точки В и С этой прямой принадлежат плоскости α .

Таким образом, плоскость α проходит через прямые а и b , следовательно является искомой.

Докажем единственность плоскости α . Допустим, что есть другая, отличная от плоскости α и проходящая через прямые а и b , плоскость β .

Так как плоскость β проходит через прямую а и не принадлежащую ей точку В , то по теореме 1 она совпадает с плоскостью α. Единственность плоскости α доказана.

— двумя параллельными прямыми.

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Теорема 3. Через две параллельные прямые можно провести единственную плоскость.

Доказательство. Пусть а и b – данные параллельные прямые. Из определения параллельных прямых следует, что через прямые а и b можно провести плоскость. Обозначим её α и убедимся, что она единственна.

Допустим противное. Пусть существует другая плоскость, отличная от α , которая содержит каждую из прямых а и b . Обозначим эту плоскость β .

Выберем на прямой а точки В и С , на прямой b – точку А . В силу параллельности прямых а и b точки А, В и С не принадлежат одной прямой.

Каждая из плоскостей α и β содержит обе прямые а и b , значит, каждая из них проходит через точки А, В и С . Но по аксиоме R 2 через эти точки можно провести лишь одну плоскость. Следовательно, плоскости α и β совпадают. Теорема доказана.

3. Взаимное расположение плоскостей в пространстве

При взаимном расположении двух плоскостей в пространстве возможен один из двух взаимно исключающих случаев.

1. Две плоскости имеют общую точку. Тогда по аксиоме пересечения двух плоскостей они имеют общую прямую. Аксиома R5 гласит: если две плоскости имеют общую точку, то пересечение этих плоскостей есть их общая прямая. Из этой аксиомы следует, что у плоскостей Такие плоскости называются пересекающимися.

2. Две плоскости не имеют общей точки.

Плоскость и прямая в пространстве

Автор: Dasha43898 • Март 18, 2018 • Реферат • 2,052 Слов (9 Страниц) • 1,377 Просмотры

РЕФЕРАТ
«Плоскость и прямая в пространстве»

ГЛАВА 1. ПЛОСКОСТЬ В ПРОСТРАНСТЕ…………. ……………. …. 4

1.1. Уравнение плоскости, проходящей через заданную точку…………. 4

1.2. Уравнение плоскости в «отрезках»………. ………………………. 5

1.3. Уравнение плоскости, проходящей через три точки….. . 5

1.4. Расстояние от точки до плоскости………………..……………………..6

ГЛАВА 2. ПРЯМАЯ В ПРОСТРАНСТВЕ…………………………………..7

2.1. Каноническое уравнение прямой………………………………….…….7

2.2. Параметрическое уравнение прямой…………………………………. 8

2.3. Уравнение прямой, как линии пересечения двух плоскостей………. 8

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ………..……………….10

Плоскость – это множество, элементами которого являются точки и в котором выполняется система аксиом планиметрии, описывающая свойства точек и прямых.

Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.

Пространство – это множество, элементами которого являются точки и в котором выполняется система аксиом стереометрии, описывающая свойства точек, прямых и плоскостей.

Цель: изучить прямую и плоскость в пространстве.

Для выполнения этой цели поставлены следующие задачи:

— рассмотреть общее уравнение плоскости;

— вывести уравнение плоскости в отрезках;

— рассмотреть каноническое и параметрическое уравнение прямой.

ГЛАВА 1. ПЛОСКОСТЬ В ПРОСТРАНСТВЕ

1. . Уравнение плоскости, проходящей через заданную точку

Уравнением поверхности в пространстве Oxyz называется такое уравнение между переменными x, y, z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности.

Назовем нормалью к плоскости вектор, перпендикулярный к этой плоскости. Обозначают нормаль [pic 1] [pic 2] =.

Пусть точки М 0 и М лежат на плоскости. Тогда n ⊥ M 0 M и, значит, их скалярное произведение равно нулю. [pic 3] [pic 4]

Общее уравнение называется полным, если все коэффициенты A,B,C,D отличны от нуля.

Уравнение плоскости, проходящей через точку перпендикулярно вектору:

A(x-x 0 )+B(y-y 0 )+C(z-z 0 )=0 (1)

Из предыдущего уравнения можно получить общее уравнение плоскости:

Виды неполных уравнений:

1. D=0, Ax+By+Cz=0 – плоскость проходит через начало координат.
2. A=0, By+Cz+D=0 – плоскость параллельна оси OX.
3. B=0, Ax+Cz+D=0 – плоскость параллельна оси OY.
4. C=0, Ax+By+D=0 – плоскость параллельна оси OZ.
5. A=0, B=0, Cz+D=0 – плоскость параллельна плоскости XOY.
6. B=0, C=0, Ax+D=0 – плоскость параллельна плоскости YOZ.
7. A=0, C=0, By+D=0 – плоскость параллельна плоскости XOZ.
8. B=0, C=0, D=0, Ax=0 => x=0 – уравнение плоскости YOZ.
9. A=0, C=0, D=0, By=0 => y=0 – уравнение плоскости XOZ.
10. A=0, B=0, D=0, Cz=0 => z=0 – уравнение плоскости XOY.

1.2. Уравнение плоскости в «отрезках»

Запишем общее уравнение плоскости:

Перенесем свободный член в правую часть уравнения и разделим на него все слагаемые: