Линейные системы уравнений — реферат
Тема: «Линейные системы уравнений»
1. Уравнения, векторы, матрицы, алгебра
2. Умножение матриц как внешнее произведение векторов
3. Нормы векторов и матриц
4. Матрицы и определители
5. Собственные значения и собственные векторы
6. Ортогональные матрицы из собственных векторов
7. Функции с матричным аргументом
8. Вычисление проекторов матрицы
Пример использования числовых характеристик матриц
10. Оценка величины и нахождение собственных значений
1. Уравнения, векторы, матрицы, линейная алгебра
Многие из рассмотренных нами задач сводились к формированию систем линейных алгебраических или дифференциальных уравнений, которые требовалось решить. Пока системы включали в себя не более трех-четырех переменных, их несложно было решать известными классическими методами: методом определителей (Крамера) или методом исключения переменных (Гаусса). С появлением цифровых вычислительных машин порядок алгебраических уравнений, решаемых методом исключений вырос в несколько десятков раз. Однако выявилось множество причин, по которым решение таких систем получить не удавалось. Появившиеся различные модификации метода исключения не привели к существенным улучшениям ситуации с получением решений. Появление же систем с количеством переменных более многих сотен и тысяч заставили обратиться и развивать итерационные методы и методы эквивалентных векторно-матричных преобразований применительно к решению линейных систем алгебраических уравнений.
Основные теоретические результаты были получены путем обобщения известных классических методов функционального анализа и алгебры конечномерных линейных пространств на векторно-матричные представления систем линейных алгебраических и дифференциальных уравнений.
Общая форма записи линейной системы алгебраических уравнений с n неизвестными может быть представлена следующим образом:
Здесь 


Последовательность записи уравнений в системе и обозначение неизвестных в последней не играет роли. В этом плане удобно при анализе и исследованиях системы использовать упорядоченную индексацию натурального ряда для неизвестных, значений правых частей и коэффициентов в уравнениях, однозначно привязывая, тем самым, каждое слагаемое и каждое уравнение к определенной позиции в общей записи. В результате можно выделить в данной записи уравнений три позиционно упорядоченных неделимых объекта:
список переменных – 
список правых частей – 
матрицу коэффициентов – 
Первые два объекта в линейной алгебре называют вектором-строкой , а второй – квадратной матрицей.
Операции с векторами, матрицами должны быть определены так, чтобы однозначно отображать допустимые эквивалентные преобразования исходной системы алгебраических уравнений. В предельных случаях задания векторов и матриц: 

Если рассмотреть i- тую строку исходной системы

то в ней кроме упорядоченного расположения компонент 



Скалярное произведение линейно, так как обладает основными свойствами линейных преобразований 
Определение скалярного произведения позволяет переписать исходную систему уравнений в виде вектора с компонентами из скалярных произведений:

Вторая форма представления векторов в форме столбцов более наглядна в смысле зрительного установления покомпонентного равенства двух векторов: стоящего слева от знака равенства и справа. Эта форма, форма вектора-столбца принята за каноническую (основную).
Левый вектор-столбец в записи каждой строки содержит вектор неизвестных и естественно желание вынести его за прямые скобки. Оставшиеся коэффициенты упорядочены, как в матрице 



Аксиоматическое построение линейной (векторной) алгебры с рассмотренными базовыми операциями позволило установить важные и полезные свойства, как самих объектов алгебры, так и их алгебраических выражений.
2. Умножение векторов и матриц
Среди n- мерных векторов и векторных операций над ними важно выделить сумму n векторов, умноженных на числовые константы:

которая при произвольном выборе 




Линейно независимый набор единичных векторов с геометрической точки зрения можно рассматривать как n- мерную систему координат. Набор компонент любого вектора в этой n- мерной системе определяет координаты точки конца вектора, исходящего из начала координат, а также являются длинами проекций вектора на координатных осях.
Среди матриц размера 


Фактически мы имеем дело с заменой системы координат. Рассмотрим методику вычисления коэффициентов результирующей матрицы уравнения:

где 


Произведение матриц в общем случае не коммутативно. Ассоциативный и распределительный законы в матричных выражениях выполняются.
3. Нормы векторов и матриц
Интерпретация упорядоченного набора чисел, как вектора в многомерном пространстве, позволяет говорить и о его длине. В прямоугольной системе координат по известным длинам проекций на координатные оси длину самого вектора вычисляют, как корень квадратный из суммы квадратов проекций:

где 


В качестве нормы в литературе иногда используют квадрат длины вектора или другое выражение с компонентами вектора, лишь бы оно обладало свойствами расстояния: было положительным, линейным и удовлетворяло неравенству треугольника.
Деление вектора на величину его нормы называют нормированием , т.е. приведением вектора к единичной длине.
Норма матрицы в принципе тоже может быть определена в виде корня квадратного из суммы квадратов ее элементов или другими выражениями со свойствами расстояний. Однако в ряде случаев работы с векторно-матричными выражениями нормы векторов и матриц должны быть согласованными ввиду того, что результатом произведения матрицы на вектор является опять же вектор. Если выражение для нормы вектора принято, то

где функция sup говорит о том, что из всех отношений норм, стоящих в числителе и знаменателе, взятых при любом векторе x , кроме нулевого, выбирается наименьшее, т.е. это функция выбора нижней границы значений. Согласованная матричная норма для евклидовой нормы вектора удовлетворяет неравенству

Нормы вектора и матрицы служат, в основном, для сопоставительной оценки матриц и векторов, указывая на возможный диапазон представления строгих числовых характеристик. К числу последних, в первую очередь, нужно отнести определители матриц, собственные значения и собственные векторы матриц и ряд других.
4. Матрицы и определители
Упорядоченный набор коэффициентов из системы линейных алгебраических уравнений используется для получения числовой характеристики, величина которой инвариантна по отношению к эквивалентным преобразованиям системы. Речь идет об определителе матрицы. Важное свойство определителей матрицы обнаруживается в связи с вычислением произведения матриц:
Учитывая это свойство и зная, что определитель единичной матрицы det(E )=1, можно найти матрицу B и ее определитель из уравнения:
откуда следует, что 

Из свойств определителей нелишне помнить и такие:
где 
n – размер квадратной матрицы A ,

s, c= 0,1,…, n – число выполненных перестановок строк и / или столбцов.
Если обратная матрица исходной системы уравнений определена, то, используя эквивалентные преобразования их векторно-матричной записи, решение уравнений можно представить в следующем виде:
Умножив вектор правых частей на обратную матрицу, получим вектор решения.
Классический способ вычисления обратной матрицы использует определители и осуществляется по формуле:

где 

Такой способ вычисления определителя представляет в основном теоретический интерес, так как требует выполнения неоправданно большого числа операций.
Очень просто вычисляется определитель, если матрица диагональная или треугольная. В этом случае определитель равен произведению диагональных элементов. Кстати и решения уравнений, имеющих такие матрицы коэффициентов, получаются тривиально. Поэтому основные усилия разработчиков методов решения алгебраических уравнений направлены на поиск и обоснование эквивалентных преобразований матрицы с сохранением всех ее числовых характеристик, но имеющих в конце преобразований диагональную или треугольную форму.
5. Собственные значения и собственные векторы
Рассмотрим теоретические основы и методы, позволяющие выполнять эквивалентные матричные преобразования.
Найдем вектор, который под воздействием матрицы A изменяет только свою величину, но не направление. Для системы уравнений это означает, что вектор решения должен быть пропорционален с некоторым коэффициентом вектору правой части:
В результате несложных преобразований получены однородные векторно-матричные уравнения в столбцовой и в строчной формах с некоторым числовым параметром 

Полагая, что решение все же существует, т.е. 

Раскрыв определитель и сгруппировав слагаемые при одинаковых степенях неизвестного параметра, получим алгебраическое уравнение степени n относительно 
Это уравнение называется характеристическим уравнением матрицы и имеет в общем случае n корней, возможно комплексных, которые называются собственными значениями матрицы и в совокупности составляют спектр матрицы . Относительно n корней различают два случая: все корни различные или некоторые корни кратные.
Важным свойством характеристического уравнения матрицы A является то, что согласно теореме Гамильтона-Кели, матрица A удовлетворяет ему:
где 
Подставляя каждое 


Решение однородных уравнений имеет некоторую специфику. Если 

Если все собственные числа различны, то собственные векторы матрицы A образуют систему n линейно независимых векторов таких, что
6. Ортогональные матрицы из собственных векторов
Из правых собственных векторов можно составить матрицу T, а из левых – матрицу 
Умножив матрицу A слева на матрицу 

Каждое скалярное произведение 
Поэтому, результатом преобразования матрицы A будет диагональная матрица с собственными значениями, расположенными на диагонали:
Если вместо A взять единичную матрицу и проделать аналогичные преобразования, то станет очевидным равенство 

Последнее показывает, что умножение матрицы A на 
Продолжая использовать T- матрицу, несложно получить следующие важные результаты:

7. Функции с матричным аргументом
Пусть теперь задана некоторая матричная функция от матрицы A :

С другой стороны очевидно и обратное

где 

где 



Проекторы обладают свойствами идемпотентных матриц , т.е. матриц, все степени которых равны первой. Для невырожденных проекторов ( 

Представление функции от матрицы A в виде взвешенной суммы проекций называется спектральным разложением матричной функции по собственным значениям матрицы A :

Если в качестве матричных функций взять 

8. Вычисление проекторов матрицы
Проекторы матрицы можно также вычислить, воспользовавшись интерполяционным многочленом Лагранжа с матричным аргументом:
По известному спектру 
Записывая разложение для каждой функции, получим следующую систему линейных уравнений относительно проекторов:
В случае, когда в спектре матрицы имеются кратные собственные значения, вычисление проекторов осуществляется по интерполяционным формулам Лагранжа, учитывающим еще и заданные значения производных в отдельных точках. Разложение матричной функции по значениям ее на спектре в этом случае имеет вид:
где 




9. Пример использования числовых характеристик матриц
Знание собственных значений матрицы и ее проекторов позволяет выполнять вычисления аналитических функций получающихся, например, при решениях систем линейных дифференциальных уравнений, при исследованиях эквивалентных матричных преобразований и пр.
Для примера построим матрицу с заданными собственными значениями 

Сначала необходимо убедиться в линейной независимости исходных векторов и добиться того, чтобы левые и правые одноименные собственные векторы оказались ортогональными, т.е. 
Для заданных векторов построим систему векторов 

Откуда последовательно находятся коэффициенты 
Взаимной ортогональности векторов v можно было бы добиваться и так, чтобы каждый 



Определитель этой системы называют определителем Грама :

где 

Если грамиан положителен, а он всегда неотрицателен, то векторы 
Для заданного выше набора векторов 
Таким образом, заданная система векторов линейно независима. Для построения ортонормированной системы векторов последовательно вычислим коэффициенты и ортогональные векторы:
После нормирования векторы образуют правую систему собственных векторов. Транспонированная Т -матрица с этими векторами есть 


Внешнее (матричное) произведение каждого нормированного вектора 
Умножая каждое собственное значение 

Аналогично получается обратная матрица:

С помощью этих же проекторов вычисляется любая аналитическая функция, аргументом которой является матрица A :

10. Оценка величины и нахождение собственных значений
Краткое рассмотрение основных теоретических положений линейной алгебры позволяет сделать следующие выводы: для успешного решения систем линейных алгебраических уравнений и вычислений матричных функций необходимо уметь находить ее собственные значения и собственные векторы.
Для любой матрицы A с действительными компонентами и любого ненулевого вектора v существует отношение Рэлея, связывающее скалярное произведение векторов v и Av с минимальным и максимальным собственными значениями:

К высказанному необходимо сделать еще ряд замечаний, связанных со случаями, когда исходная матрица имеет кратные собственные значения или оказывается вырожденной.
Характеристическое уравнение матрицы A с кратным корнем 

На основании этой записи можно составить минимальное характеристическое уравнение 

Особенности в части определения собственных значений и векторов обычно возникают в несимметричных матрицах ( 


где A – произвольная матрица размера 


V – некоторая невырожденная матрица размера 
Характеристическое уравнение жорданова блока размера 



Если выразить матрицу V в форме вектора с компонентами в виде векторов-столбцов 

Здесь 

При поиске решений систем линейных уравнений с несимметричными матрицами, последние стремятся теми или иными приемами свести к выражению с симметричными матрицами.
Один из возможных подходов к решению несимметричных линейных систем состоит в замене исходной системы эквивалентной системой:

Недостаток этого подхода состоит в том, что мера обусловленности произведения матрицы A на свою транспонированную, оцениваемая отношением 
Под мерой обусловленности понимают отношение наибольшего собственного значения матрицы к наименьшему. Это отношение влияет на скорость сходимости итерационных процедур при решении уравнений.
Итак, основными алгебраическими системами уравнений можно считать неоднородные системы уравнений с симметричными матрицами коэффициентов.
1. Вержбицкий В.М. Основы численных методов: Учебник для вузов – 3-е изд. М: Высшая школа, 2009. – 840 с.
2. Самарcкий А.А. Задачи и упражнения по численным методам. Изд. 3 Изд-во: КомКнига, ЛКИ, 2006. – 208 с.
3. Турчак Л.И., Плотников П.В. Основы численных методов. Изд-во: ФИЗМАТЛИТ®, 2003. – 304 с.
4. Хеннер Е.К., Лапчик М.П., Рагулина М.И. Численные методы. Изд-во: «Академия/Academia», 2004. – 384c.
Реферат: Система линейных уравнений
1. Основные понятия
2. Система n линейных уравнений с n неизвестными. Правило Крамера
3. Однородная система п линейных уравнений, с n неизвестными
4. Метод Гаусса решения общей системы с линейных уравнений
5. Критерий совместности общей системы линейных уравнений
Многие теоретические и практические вопросы приводят не к одному уравнению, а к целой системе уравнений с несколькими неизвестными. Особенно важен случай системы линейных уравнений, т.е. системы m уравнений 1ой степени сn неизвестными:
a11 x1 + … + a1n xn = b1 ;
a21 x1 + … + a2n x n = b2;
Здесь x1, …, xn – неизвестные, а коэффициенты записаны так, что индексы при них указывают на номер уравнения и номер неизвестного. Значение систем 1-й степени определяется не только тем, что они простейшие. На практике часто имеют дело с заведомо малыми величинами, старшими степенями которых можно пренебречь, так что уравнения с такими величинами сводятся в первом приближении к линейным. Не менее важно, что решение систем линейных уравнений составляет существенную часть при численном решении разнообразных прикладных задач.
Способы решения систем линейных уравнений – очень интересная и важная тема. Системы уравнений и методы их решения рассматриваются в школьном курсе математики, но недостаточно широко. А для того, чтобы перейти к исследованию данной темы, также нужно было познакомиться с темой матриц и определителей. Этот же материал вообще в школьной программе не изучается. В процессе знакомства с данной работой приобретаются навыки, с помощью которых в последующем решение систем линейных уравнений станет намного проще, понятнее и быстрее.
Цель моей работы заключается в том, чтобы изучить различные способы решения систем линейных уравнений для применения их на практике.
1. Основные понятия
В самом общем случае система линейных уравнений имеет следующий вид:
a11 x1 + a12 x2 + …+ a1n xn = b1 ;
a21 x1 + a22 x2 + …+ a2n xn = b2; (1)
где х1, х2, …, х n — неизвестные, значения которых подлежат нахождению. Как видно из структуры системы (1), в общем случае число неизвестных не обязательно должно быть равно числу уравнений самой системы. Числа а11, а12, …, а mn называются коэффициентами системы, а b 1 , b 2 , …, bm — её свободными членами. Для удобства коэффициенты системы а ij (i =1, 2. m ; j = 1, 2. n ) и свободные члены bi (i =1, 2. m ) снабжены индексами. Первый индекс коэффициентов а ij соответствует номеру уравнения, а второй индекс – номеру неизвестной х i, при которой коэффициент поставлен. Индекс свободного члена bi соответствует номеру уравнения, в которое входит bi .
Дадим определения некоторых понятий, необходимых при изучении системы уравнений. Решением системы уравнений (1) называется всякая совокупность чисел α 1 , α 2 , αn , которая будучи поставлена в систему (1) на место неизвестных х1, х2, …, х n , обращает все уравнения системы в тождества. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если не имеет решений. Совместная система уравнений называется определенной, если она имеет одно единственное решение, и неопределенной, если она имеет по крайней мере два различных решения.
Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и тоже множество решений.
2. Система n линейных уравнений с n неизвестными. Правило Крамера
Пусть дана система n линейных уравнений с n неизвестными:
a11 x1 + a12 x2 + …+ a1n xn = b1 ;
a21 x1 + a22 x2 + …+ a2n xn = b2; (2)
Определителем системы (2) называется определитель, составленный из коэффициентов а ij.
Рассмотрим случай, когда ∆ ≠ 0. Докажем, что в этом случае система (2) является определенной, т.е. имеет одно единственное решение. Как и ранее, через А ij будем обозначатьалгебраическое дополнение элемента а ij в определителе ∆.
Умножим каждое уравнение системы (2) на алгебраические дополнения элементов i -го столбца определителя ∆, т.е. первое уравнение умножим на А1 i, второе – на А2 i и т.д., наконец, последнее уравнение – на А ni, а затем все полученные уравнения системы сложим. Врезультатебудемиметь
(a11 x1 + a12 x2 + …+ a1i xi + …+ a1n xn )A1i + (a21 x1 + a22 x2 + …+ a2i xi +
+ …+ a2n xn )A2i + …+ (an1 x1 + an2 x2 + …+ ani xi + …+ an xnn )Ani = b1 A1i + b2 A2i + …+ bn Ani
или, сгруппировав члены относительно известных x 1 , x 2 , …, xn , получим
(a11 A1i + a21 A2i + …+ an1 Ani )x1 + … +
+ (a1i A1i + a2i A2i + …+ ani Ani )xi + … +
+ (a1n A1i + a2n A2i + …+ ann Ani ) xn =
= b1 A1i + b2 A2i + …+ bn Ani . (3)
Коэффициент при неизвестной х i равен определителю ∆, а коэффициенты при всех других неизвестных равны нулю. Свободный член уравнения (3) отличается от коэффициента при х1 тем, что коэффициенты а1 i , а2 i , …, а ni заменены свободными членами b 1 , b 2 , …, bn уравнения (2). Следовательно, выражение b 1 A 1 i + b 2 A 2 i + …+ bn Ani есть определитель i -го порядка, отличающийся от определителя только i -м столбцом, которыйзамененстолбцом свободных членов. Обозначив этот определитель ∆ xi, будем иметь
Реферат: Способы решения систем линейных уравнений
| Название: Способы решения систем линейных уравнений Раздел: Рефераты по математике Тип: реферат Добавлен 22:42:34 10 июля 2005 Похожие работы Просмотров: 13600 Комментариев: 22 Оценило: 14 человек Средний балл: 3.9 Оценка: 4 Скачать |








































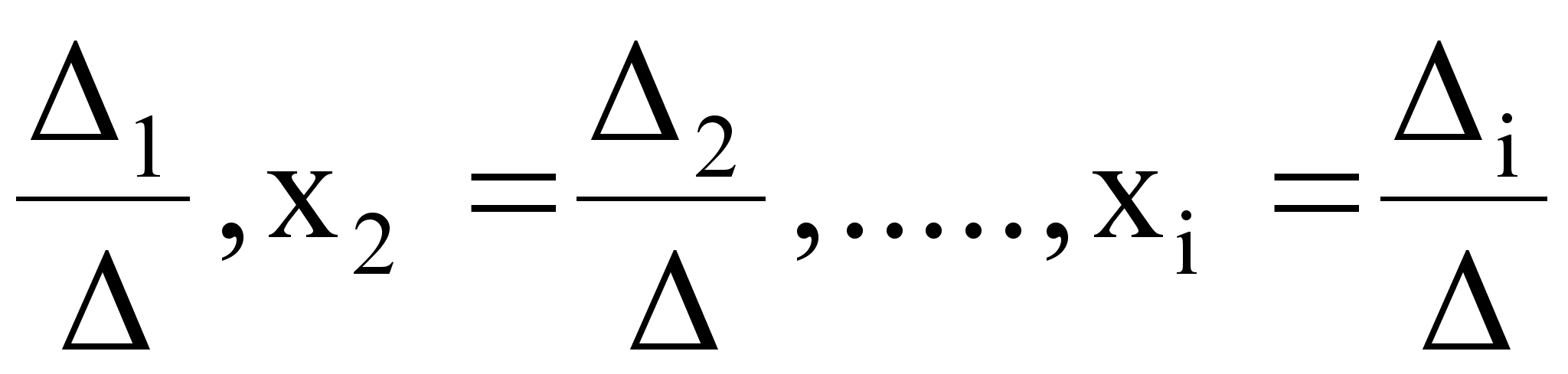 , где
, где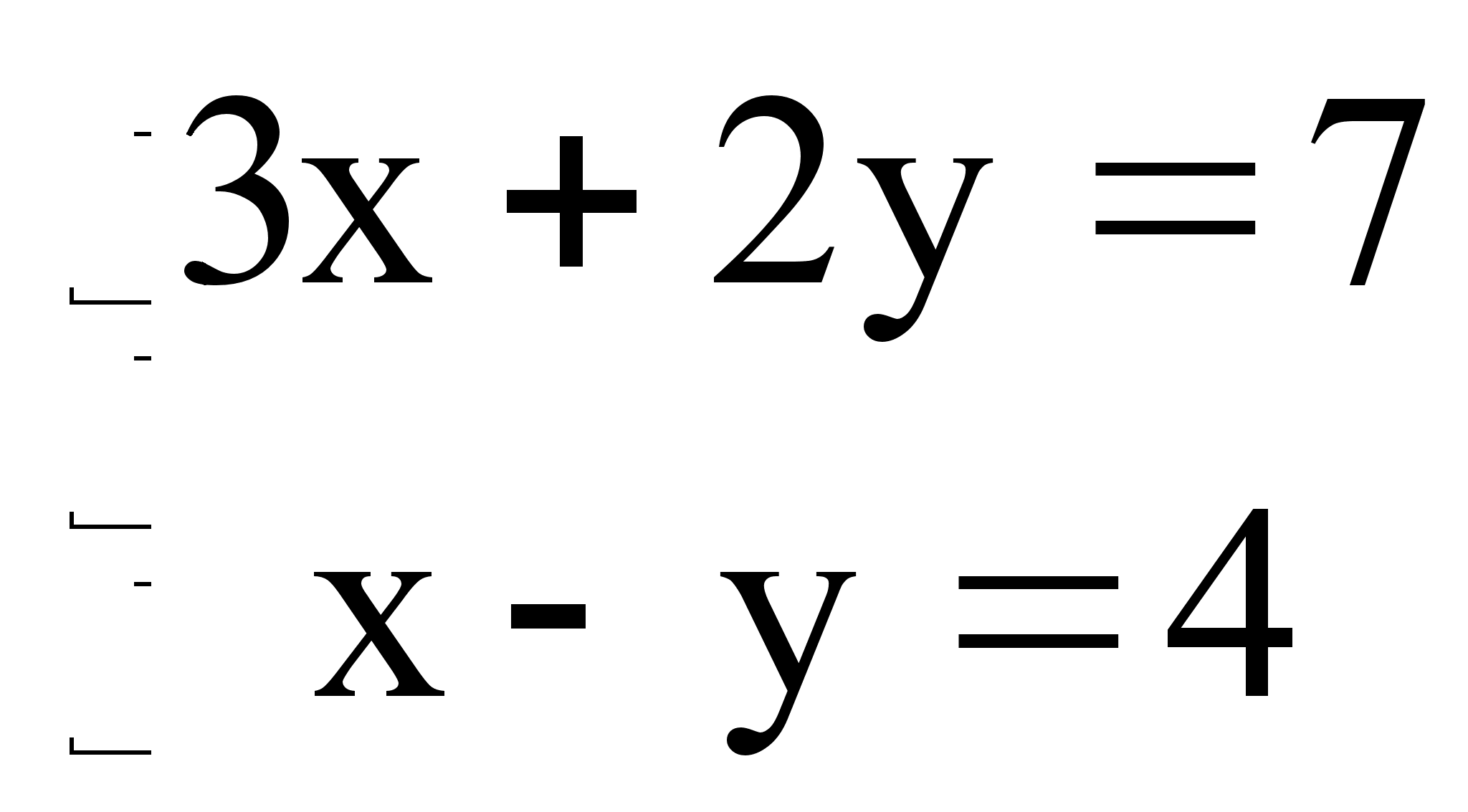 .
.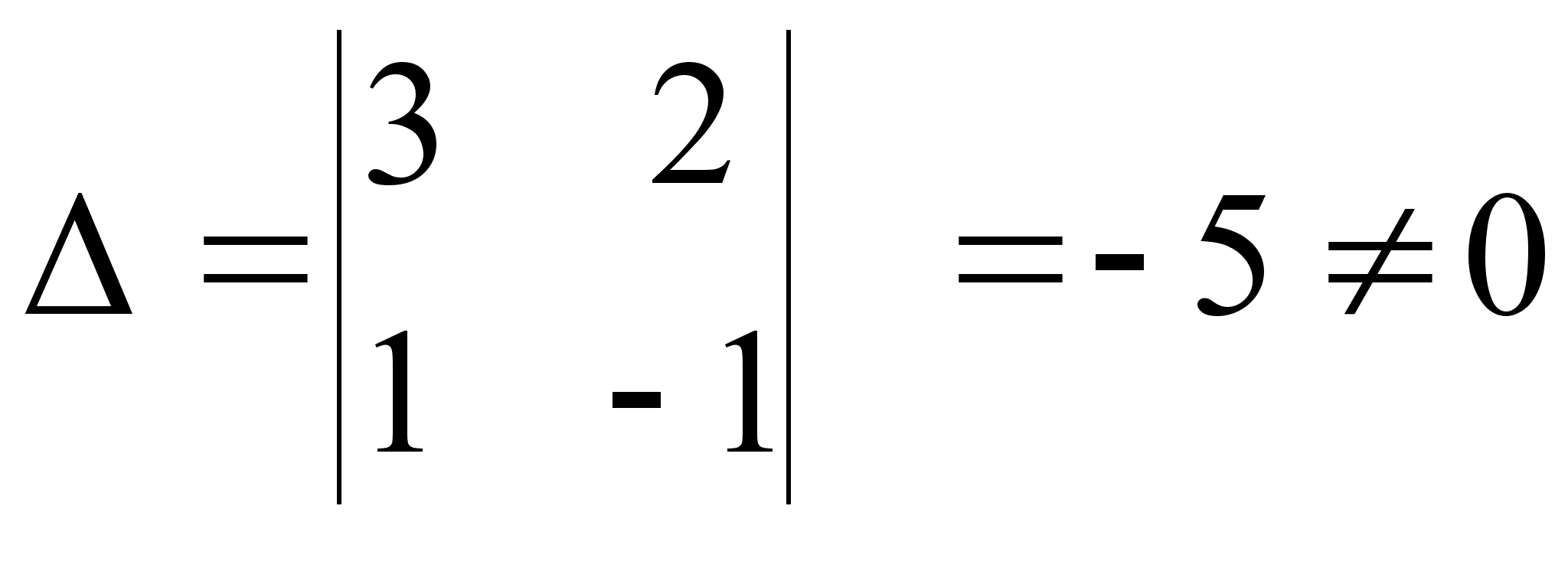
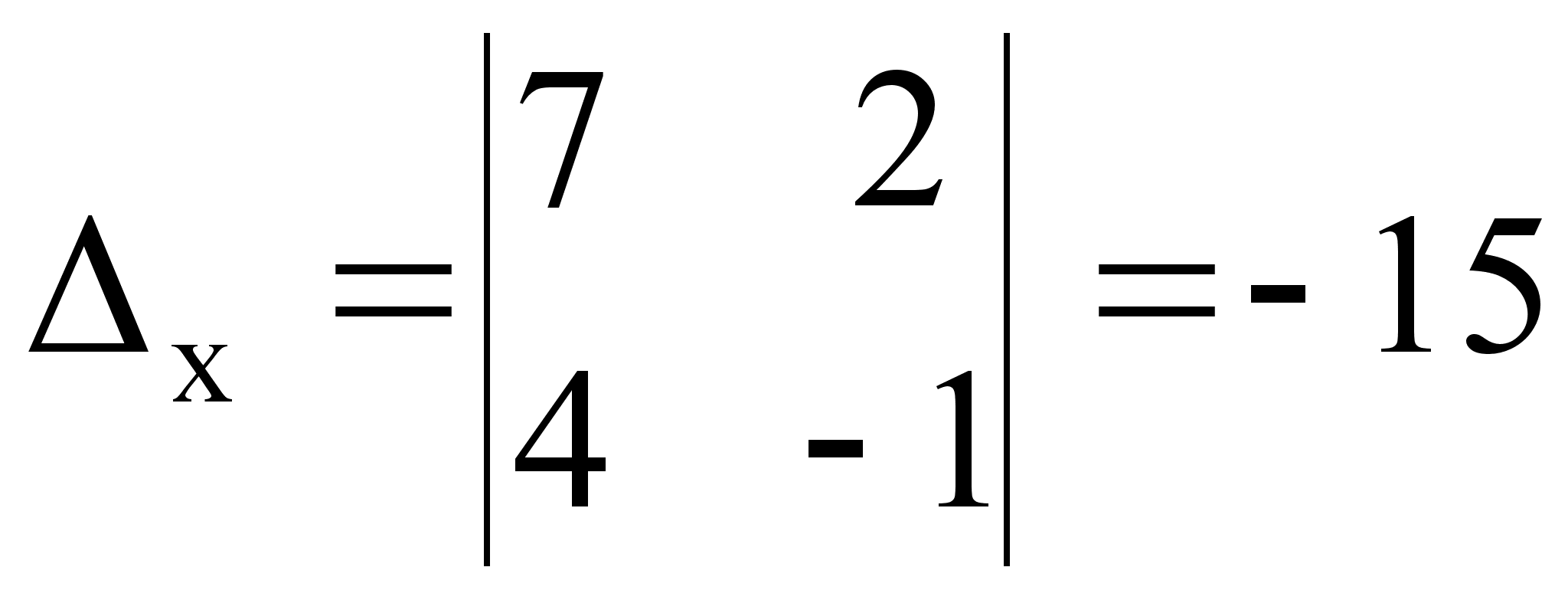
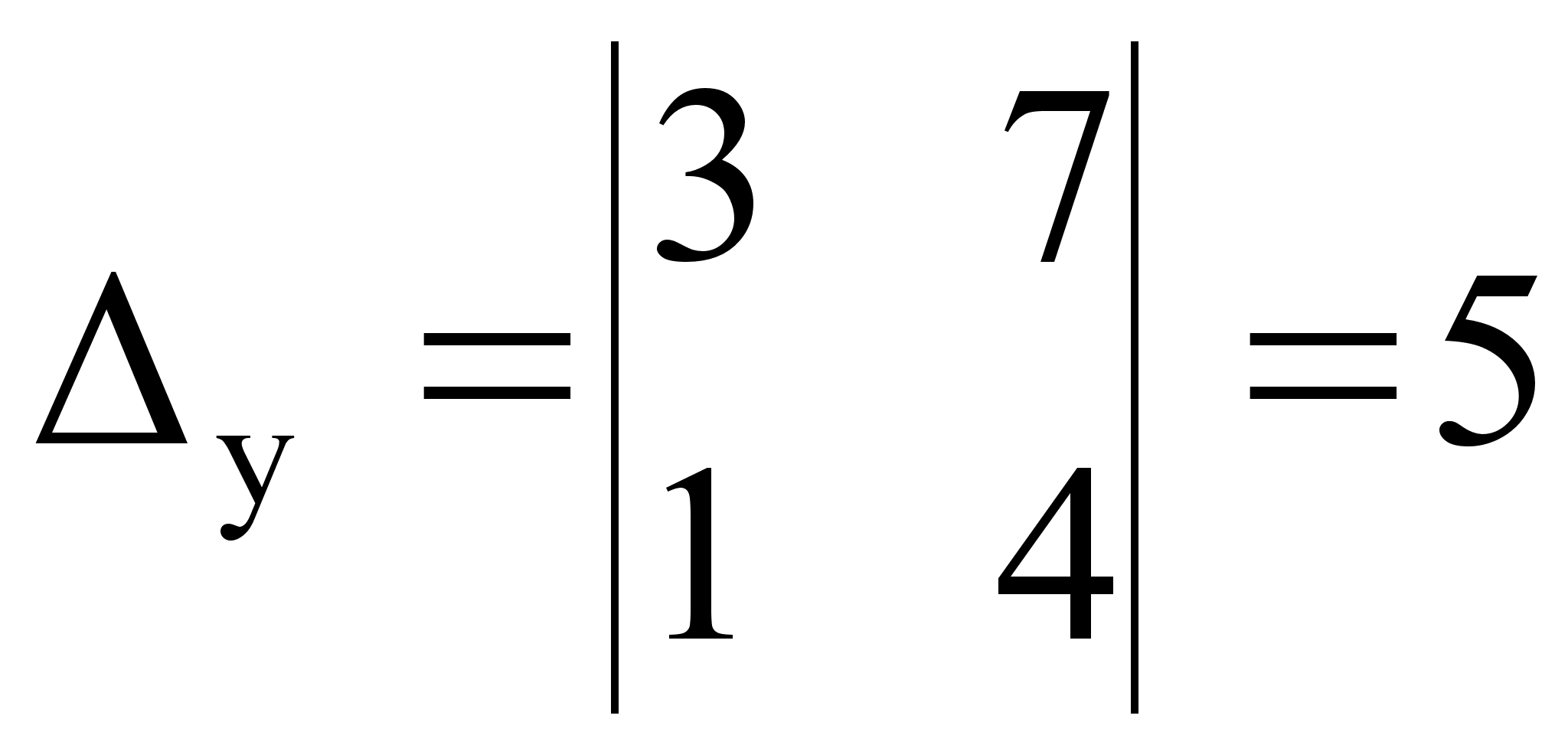
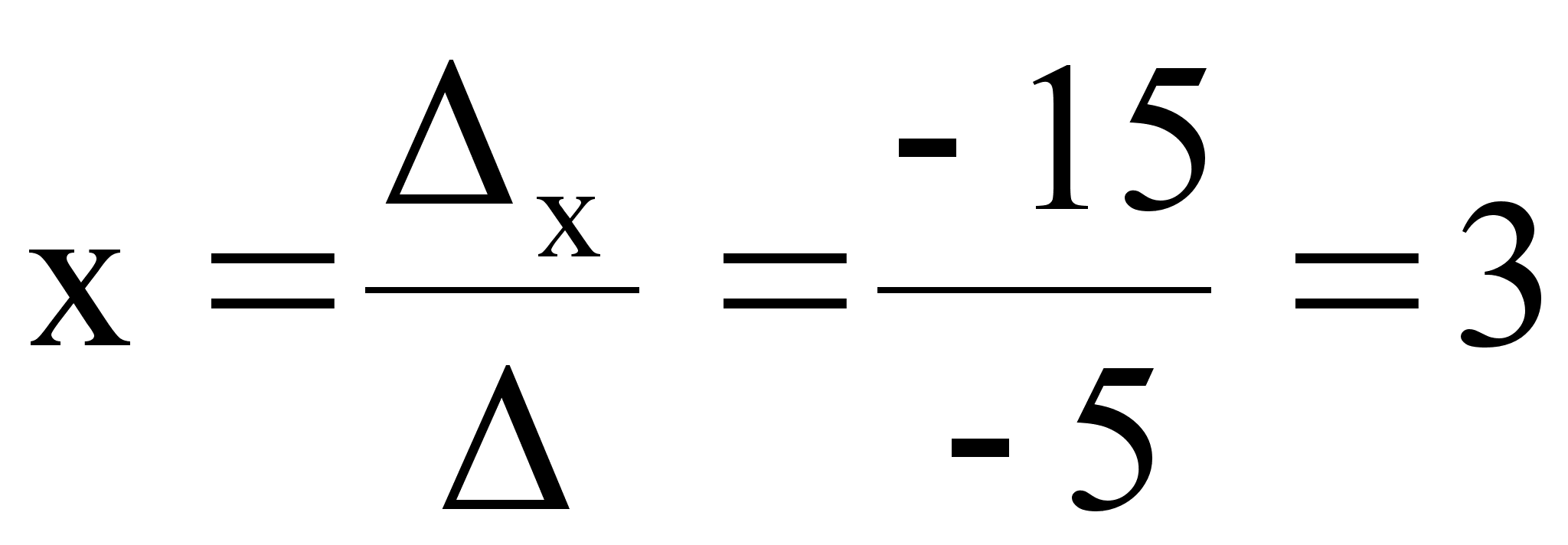
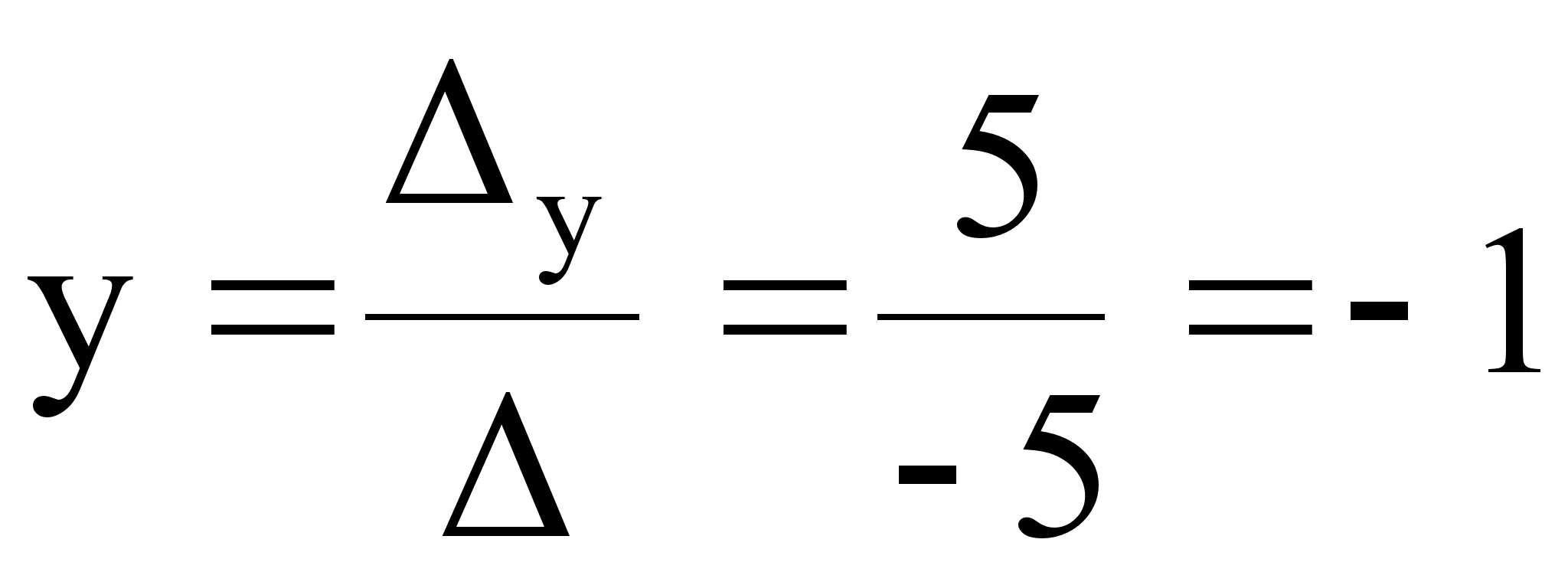 .
. так, пусть дана система, содержащая m линейных уравнений с п неизвестными:
так, пусть дана система, содержащая m линейных уравнений с п неизвестными: x 1 – 2 x 2 + x 3 + x 4 = –1;
x 1 – 2 x 2 + x 3 + x 4 = –1;
 x 1 – 2 x 2 + x 3 + x 4 = –1;
x 1 – 2 x 2 + x 3 + x 4 = –1; 5 x 1 – x 2 + 2 x 3 + x 4 = 7;
5 x 1 – x 2 + 2 x 3 + x 4 = 7;
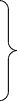 a 11 x 1 + … + a 1n x n = b 1 ;
a 11 x 1 + … + a 1n x n = b 1 ;
 1 2 3 7 8
1 2 3 7 8 А = ; В = 9 10 , то (1)
А = ; В = 9 10 , то (1)

 a 11 a 12 … a 1r a 1 l
a 11 a 12 … a 1r a 1 l