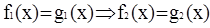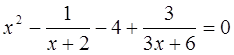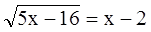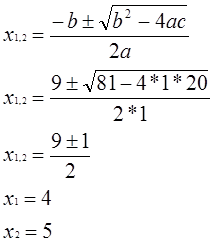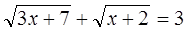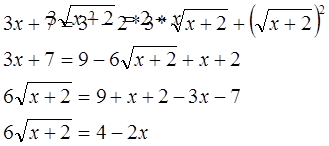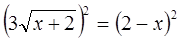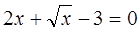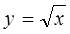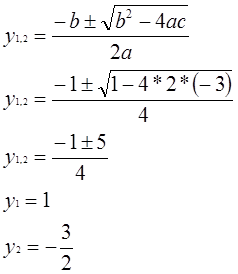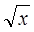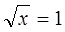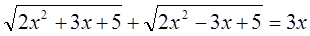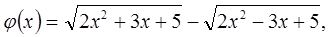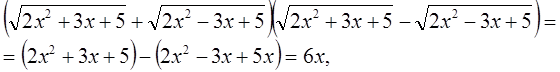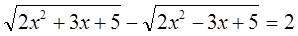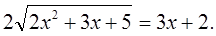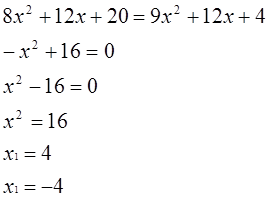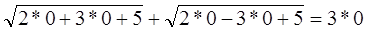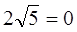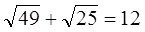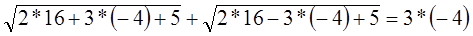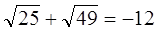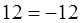Реферат рациональные и иррациональные уравнения

Реферат: Иррациональные уравнения

В школьном курсе алгебры рассматриваются различные виды уравнений – линейные, квадратные, биквадратные, кубические, рациональные, с параметрами, иррациональные и другие. Данная курсовая работа посвящена иррациональным уравнениям, методам их решения. Кроме того, в работе введены понятия уравнений следствий и равносильных уравнений, а также приведены примеры задач, математическими моделями которых служат иррациональные уравнения. В данной работе содержится небольшая историческая справка, посвященная введению иррациональных чисел.

Термин «рациональное» (число) происходит от латиноамериканского слова ratio – отношение, которое является переводом греческого слова “логос”в отличие от рациональных чисел, числа, выражающие отношение несоизмеримых величин, были названы еще в древности иррациональными, т.е. нерациональными (по-гречески “алогос”) правда, первоначально термины “рациональный” и “иррациональный” относились не к числам, а к соизмеримым и соответственно не соизмеримым величинам, которые пифагорейцы называли выразимыми и невыразимыми, Теодор Киренский же симметричными и ассимметричными. В V-VI вв. римские авторы Капелла и Кассиодор переводили эти термины на латынь словами rationalis и irrationalis. Термин «соизмеримый» (commensurabilis) ввел в первой половине VI в. другой римский автор- Боэций.

Древнегреческие математики классической эпохи пользовались только рациональными числами (вернее целыми, дробными и положительными). В своих «Началах» Евклид излагает учение об иррациональностях чисто геометрически.

Математики Индии, Ближнего и Среднего Востока, развивая алгебру, тригонометрию и астрономию, не могли обойтись без иррациональных величин, которые, однако, длительное время не признавали за числа. Греки называли иррациональную величину, например, корень из квадратного числа, «алогос» – невыразимое словами, а позже европейские переводчики с арабского на латынь перевели это слово латинским словом surdus – глухой. В Европе термин surdus- глухой впервые появился в середине XII в. у Герарда Кремонского, известного переводчика математических прозведений с арабского на латынь, затем у итальянского математика Леонардо Фабоначчи и других европейских математиков, вплоть до XVIII в. Правда уже в XVI в. Отдельные ученые, в первую очередь итальянский математик Рафаэль Бомбелли и нидерландский математик Симон Стевин считали понятие иррационального числа равноправным с понятием рационального числа. Стевин писал: «Мы приходим к выводу, что не существует никаких абсурдных, иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной закономерностью.»

Еще до Бомбелли и Стевина многие ученые стран Среднего Востока в своих трудах употребляли иррациональные числа как полноправные объекты алгебры. Более того, комментируя «Начала» Евклида и исследуя общую теорию отношения Евдокса, Омар Хайям уже в начале XII в. теоретически расширяет понятие числа до положительного действительного числа. В том же направлении много было сделано крупнейшим математиком XIII в. ат-Туси.

Математики и астрономы Ближнего и Среднего Востока вслед за астрономами древнего Вавилона и эллинистической эпохи широко пользовались шестидесятеричными дробями, арифметические действия с которыми они называли «арифметикой астрономов». По аналогии с шестидесятеричными дробями самаркандский ученый XV в. ал-Каши в работе «Ключ арифметики» ввел десятичные дроби которыми он пользовался для повышения точности извлечения корней. Независимо от него по такому же пути шел открывший в 1585 г. десятичные дроби в Европе Симон Стевин, который в своих «приложениях к алгебре» (1594 г.) показал, что десятичные дроби можно использовать для бесконечно близкого приближения к действительному числу. Таким образом, уже в XVI в. зародилась идея о том, что естественным аппаратом для введения и обоснования понятия иррационального числа являются десятичные дроби. Появление «Геометрии» Декарта облегчило понимание связи между измерением любых отрезков (и геометрических величин вообще) и необходимости расширения понятия рационального числа. На числовой оси иррациональные числа, как и рациональные, изображаются точками. Это геометрическое толкование позволило лучше понять природу иррациональных чисел и способствовало их признанию.

В современных учебных руководствах основа определения иррационального числа опирается на идеи ал-Каши, Стевина и Декарта об измерении отрезков и о неограниченном приближении к искомому числу с помощью бесконечных десятичных дробей. Однако обоснованием свойств действительных чисел и полная теория их была разработана лишь в XIX в.

2. ОПРЕДЕЛЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ

Равносильные уравнения. Следствия уравнений.

При решении уравнений выполняются различные тождественные преобразования над выражениями, входящими в уравнение. При этом исходное уравнение изменяется другими, имеющими те же корни. Такие уравнения называются равносильными.

Определение: Уравнение f(x)=g(x) равносильно уравнению f1(x)=g1(x), если каждый корень первого уравнения является корнем второго и обратно, каждый корень второго уравнения является корнем первого, т.е. их решения совпадают.

Например, уравнения 3x-6=0; 2х–1=3 равносильны, т.к. каждое из уравнений имеет один корень х=2.

Любые два уравнения, имеющие пустое множество корней, считают равносильными.

Тот факт, что уравнения f(x)=g(x) и f1(x)=g1(x) равносильны, обозначают так:

Название: Иррациональные уравнения
Раздел: Рефераты по математике
Тип: реферат Добавлен 02:52:28 21 марта 2003 Похожие работы
Просмотров: 7276 Комментариев: 29 Оценило: 20 человек Средний балл: 3.3 Оценка: 3 Скачать

f(x)=g(x) f1(x)=g1(x)

В процессе решения уравнений важно знать, при каких преобразованиях данное уравнение переходит в равносильное ему уравнение.

Теорема 1: Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив его знак, то получим уравнение, равносильное данному.

Доказательство:
Докажем, что уравнение f(x) = g(x)+q(x) (1)
равносильно уравнению

Пусть х=а – корень уравнения. Значит имеет место числовое равенство f(a)=g(a)+q(a) . Но тогда по свойству действительных чисел будет выполняться и числовое равенство f(a)-q(a)=g(a) показывающее, что а – корень уравнения (2). Аналогично доказывается, что каждый корень уравнения (2) является и корнем уравнения (1).

Что и требовалось доказатью.

Теорема 2: Если обе части уравнения умножить или разделить на отличное от нуля число, то получим уравнение, равносильное данному.

Доказательство: докажем, что уравнение 6х–3=0 равносильно уравнению 2х–1=0

решим уравнение 6х–3=0 и уравнение 2х–1=0

так как корни уравнений равны, то уравнения равносильны.

Что и требовалось доказать.

ОДЗ этого уравнения

Мы знаем, что дробь равна нулю в том случае, когда ее числитель равен нулю, т.е. х²+х–2=0, а знаменатель не равен 0. Решая уравнение х²+х–2=0, находим корни х1=1, х2 = –2 . Но число 1 не входит в ОДЗ данного уравнения и значит, исходное уравнение имеет один корень х=-2.

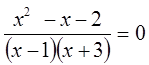
В этом случае говорят, что уравнение х²+х–2=0, есть следствие уравнения

пусть даны два уравнения:

Если каждый корень уравнения (3) является корнем уравнения (4), то уравнение (4) называют следствием уравнения (3).

Этот факт записывают так:

В том случае, когда уравнение (3) — есть также следствие уравнения (4), эти уравнения равносильны.

Два уравнения равносильны в том, и только в том случае, когда каждое из них является следствием другого.

В приведенном выше примере уравнение – следствие
х²+х–2=0, имеет два корня x1=1 и х2 =-2, а исходное уравнение имеет один корень х=-2. В этом случае корень х=1 называют посторонним для исходного уравнения

В общем случае корни уравнения-следствия, не являющиеся корнями исходного уравнения, называют посторонними.

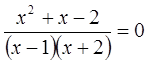
Итак, если при решении уравнения происходит переход к уравнению – следствию, то могли появиться посторонние корни. В этом случае все корни уравнения-следствия нужно проверить, подставляя их в исходное уравнение. В некоторых случаях выявление посторонних корней облегчается знанием ОДЗ исходного уравнения – корни, не принадлежащие ОДЗ, можно сразу отбросить. Так, в приведенном примере посторонний корень х=1 не входит в ОДЗ уравнения и потому отброшен.

Иногда посторонние корни могут появиться и при тождественных преобразованиях, если они приводят к изменению ОДЗ уравнения. Например, после приведения подобных членов в левой части уравнения

получим уравнение следствие х²-4=0 имеющее два корня х1 = 2, х2 = -2 корень х2 = -2 – посторонний, так как не входит в ОДЗ исходного уравнения.

В тех случаях, когда в результате преобразований произошел переход от исходного уравнения к уравнению, не являющемуся его следствием, возможна потеря корней.

Например, уравнение (х+1)(х+3)= х+1 (5)

Имеет два корня. Действительно, перенося все члены уравнения в левую часть и вынося х+1 за скобки, получим (х+1)(х+2)=0, откуда находим х1=-1, х2=-2 .

Если же обе части уравнения (5) разделить («сократить») на х+1, то получим уравнение х+3=1, имеющее один корень х=-2. В результате такого преобразования корень х=-1 потерян. Поэтому делить обе части уравнения на выражение, содержащее переменную, можно лишь в том случае, когда это выражение отлично от нуля.

Для того, чтобы в процессе решения уравнения избежать потери корней, необходимо следить за тем, чтобы переход осуществлялся либо к равносильным уравнениям, либо к уравнениям-следствиям.

2.2. Определение иррациональных уравнений.

Иррациональными называются уравнения, в которых переменная содержится под знаком корня или под знаком операции возведения в дробную степень.

3. МЕТОДЫ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ.

3.1. Решение иррациональных уравнений методом возведения обеих частей уравнения в одну и ту же степень.

Решить уравнение

Возведем обе части уравнения (1) в квадрат:

далее последовательно имеем:

5х – 16 = х² — 4х + 4

х² — 4х + 4 – 5х + 16 = 0

Проверка: Подставив х=5 в уравнение (1), получим – верное равенство. Подставив х= 4 в уравнение (1), получим – верное равенство. Значит оба найденных

значения – корни уравнения.

Преобразуем уравнение к виду:

и применим метод возведения в квадрат:

далее последовательно получаем.

Разделим обе части последнего уравнения почленно на 2:

еще раз применим метод возведения в квадрат:

х1 х2 = -14 х2 = -1

по теореме, обратной теореме Виета, х1=14, х2 = -1

корни уравнения х²-13х–14 =0

Проверка: подставив значение х=-14 в уравнение (2), получим–

— не верное равенство. Поэтому х = -14 – не корень уравнения (2).

Подставив значение x=-1 в уравнение (2), получим-

— верное равенство. Поэтому x=-1- корень уравнения (2).

3.2 Метод введения новых переменных.

Конечно, можно решить это уравнение методом возведения обеих частей уравнения в одну и ту же степень. Но можно решить и другим способом – методом введения новых переменных.

Введем новую переменную Тогда получим 2y²+y–3=0 – квадратное уравнение относительно переменной y. Найдем его корни:

Т.к. , то – не корень уравнения, т.к. не

может быть отрицательным числом . А — верное равенство, значит x=1- корень уравнения.

Искусственные приёмы решения иррациональных уравнений.

Умножим обе части заданного уравнения на выражение

То уравнение (1) примет вид:

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом известен. Тогда x1=0.Остаётся решить уравнение:

Сложив уравнения (1) и (2), придём к уравнению

Решая уравнение (3) методом возведения в квадрат, получим:

x1=0, x2=4, x3= -4 подставим в уравнение

— не верное равенство, значит x1=0- не корень уравнения.

— верное равенство, значит x2=4- корень уравнения.

— не верное равенство, значит x3= -4- не корень уравнения.

Итак, уравнения, которые содержат переменную под знаком корня, называются иррациональными. Иррациональные уравнения решаются в основном возведением обеих частей уравнения в квадрат (или n-ую степень) или введением новой переменной. Кроме того, пользуются и искусственными приемами решения иррациональных уравнений.

1) А.Г.Мордкович. Алгебра 8 класс. Учебник для общеобразовательных учреждений — Москва: Издательство «Мнемозина», 1999.

2) М.Я.Выгодский. Справочник по элементарной математике — Москва: Издательство «Наука», 1986.

3) А.П.Савин. Энциклопедический словарь юного математика – Москва: Издательство «Педагогика», 1989.

4) А.И.Макушевич. Детская энциклопедия – Москва: Издательство «Педагогика», 1972.

5) Н.Я.Виленкин. Алгебра для 9 класс. Учебное пособие для учащихся школ и классов с углубленным изучением изучением математики – Москва: Издательство «Просвещение», 1998.

Рациональные и иррациональные уравнения и неравенства

Автор: Пользователь скрыл имя, 10 Марта 2013 в 20:20, реферат

Краткое описание

При решении неравенств и уравнений фундаментальное значение имеет понятие равносильности, и в нашей работе это будет играть большую роль. Два неравенства
F1(x) >G1(x) иF2(x) >G2(x) или два уравненияF1(x) =G1(x) иF2(x) =G2(x)
называются равносильными на множестве X, если каждое решение первого неравенства (уравнения), принадлежащее множеству X, является решением второго и, наоборот, каждое решение второго, принадлежащее X, является решением первого; или ни одно из неравенств (уравнений) на X не имеет решений. Таким образом, неравенства (или уравнения) называются равносильными на X, если множества решений этих неравенств (уравнений) совпадают.

Файлы: 1 файл

Рациональные и иррациональные уравнения и неравенства.docx

Рациональные и иррациональные уравнения и неравенства. Степень с рациональным показателем. Понятие равносильности уравнений и неравенств.

Понятие равносильности уравнений и неравенств.
Степень с рациональным показателем.
Рациональные уравнения и неравенства.
- Рациональные уравнения.
- Метод интервалов для рациональных функций.
- Иррациональные уравнения.
  - Уравнения вида: √f(x) = g(x)
  - Уравнения вида: √f(x) = √g(x)
- Иррациональные неравенства.
  - Неравенство вида: √f(x) / √g(x) ≤ 0 (или ≥ 0)
  - Неравенство вида: √f(x) > g(x) (или значение имеет понятие равносильности, и в нашей работе это будет играть большую роль. Два неравенства
    F₁(x) >G₁(x) иF₂(x) >G₂(x) или два уравненияF₁(x) =G₁(x) иF₂(x) =G₂(x)
    называются равносильными на множестве X, если каждое решение первого неравенства (уравнения), принадлежащее множеству X, является решением второго и, наоборот, каждое решение второго, принадлежащее X, является решением первого; или ни одно из неравенств (уравнений) на X не имеет решений. Таким образом, неравенства (или уравнения) называются равносильными на X, если множества решений этих неравенств (уравнений) совпадают.
    Отсюда следует, что, вместо того чтобы решать данное неравенство (уравнение), можно решать любое другое, равносильное данному. Замену одного неравенства (уравнения) другим, равносильным данному на X, называют равносильным переходом на X. Равносильный переход обозначают двойной стрелкой . Если уравнение f(x) = 0 равносильно уравнению g(х) = 0, то это мы будем обозначать так:
    1. √sin 2 X -1 = 0 cosX = 0, т.к. решением первого уравнения являются все Х, для которых sin 2 X = 1,но sin2X + cos2X ≡ 1, поэтому при этом cosX = 0, и наоборот.
    2. √8 — Х 2 = X и 8 -Х 2 не равносильны, т.к. (-2) является решением второго уравнения, но не является решением второго.
    3. Уравнения SinX = 3 и √8 — x = -1равносильны, т.к. ни то ни другое не имеет решений.
    Отметим основные операции, приводящие к равносильным соотношениям.
    1. Если функции f(x), g(x), h(x) определены на множестве X, то на X
    f(x) f(x) + h(x) f(x) + h(x) = g(x) + h(x).
    1. Если h(x) > 0 на X, то на X
    т.е. при умножении неравенства на отрицательную функцию знак неравенства меняется на противоположный.
    1. Если h(x) ≠ 0 на X, то на X
    1. Если f(x) ≥ 0, g(x) ≥ 0 на X, то на X
    f(x) f 2 (x) 2 (x),
    f(x) = g(x) f 2 (x) =g 2 (x),
    f(x) ≤ g(x) f 2 (x) ≤ g 2 (x).
    т.е. если обе части неравенства или уравнения неотрицательны, то возведение в квадрат (или любую четную степень) обеих частей неравенства или уравнения приводит к равносильному неравенству или уравнению соответственно.
    Если левая и правая части неравенства имеют разные знаки, то нельзя возводить неравенство в квадрат, т. к. возведение в квадрат может привести как к равносильному неравенству, так и к неравносильному: -4 25.
    1(A) Решить уравнение √1 — sinХ = cosX.
    Решение с помощью равносильных преобразований.
    N — множество всех натуральных чисел.
    Z — множество всех целых чисел.
    Q — множество всех рациональных чисел.
    R — множество всех действительных чисел.
    Ø — пустое множество (нет решений).
    P_n(х) = a₀X n + a₁X n-1 + . + a_n — многочлен степени n, n € N.
    Степень с рациональным показателем.
    X n = a, n € Z.
    Начертим эскизы графиков функции у = X n для четных и нечетных n (рис. 1, 2).
    Рациональные и иррациональные уравнения и неравенства.
    Одним из способов решения уравнений высших степеней является разложение на множители многочлена, стоящего в левой части уравнения. Этот способ основан на применении теоремы Везу: если число а является корнем многочлена P_n(х), то этот многочлен можно представить в виде
    Это значит, что если известен один корень уравнения степени п, то с помощью теоремы Везу задачу можно свести к решению уравнения степени n — 1, т. е., как говорят, понизить степень уравнения. Если P_n(х) можно представить в виде (x — a) k Q_n-k(x) и число х = а не является корнем многочлена Q_n-k(x), то
    говорят, что а является корнем многочлена P_n(х) кратности k.
    Как найти хотя бы один корень? Его приходится «угадывать».
    Чтобы понять, как угадывать, приведем без доказательства теорему и ее следствия.
    Теорема1. Пусть несократимая дробь p/q является корнем уравнения a₀X_n + a₁X n-1 + . + a_n-1X + a_n = 0 с целыми коэффициентами. Тогда число p является делителем свободного члена a_n, a q — делителем а₀ — коэффициента при старшей степени X.
    Следствие 1. Любой целый корень уравнения с целыми коэффициентами является делителем его свободного члена.
    Следствие 2. Если коэффициент при старшей степени уравнения с целыми коэффициентами равен 1, то все рациональные корни уравнения, если они существуют, являются целыми числами.
    Если удалось угадать корень а, то найти частное от деления на (X — а) можно, по крайней мере, тремя способами: делением под углом; по схеме Горнера; последовательным выделением слагаемых, имеющих множитель (X — а).
    17(С2). Решите уравнение (x 2 — 1)(x + 3)(x + 5) = 20.
    □ Первый способ. Разложим все многочлены на элементарные множители (х — 1) (х +1) (х + 3) (x + 5) и нанесем их корни на числовую ось (рис. 4).
    Теперь видно, что расстояние между соседними корнями одно и то же. В таком случае, когда корней четное число, удобно сделать замену переменных t = х — x_o, где х_о — середина между крайними корнями. Тогда в уравнение войдут квадраты новой переменной. В данном случае х_о = -2. Поэтому t = х + 2 х = t — 2 и уравнение станет биквадратным:
    (t — 3)(t — 1)(t + 1)(t + 3) ≡ (t 2 — 1)(t 2 — 9) = 20 (t 2 ) 2 — 10t 2 — 11 = 0 t 2 = 5 ± 6 t 2 = 11,
    или в старых переменных x = ± √11 — 2.
    Ответ: x = ± √11 — 2.
    □ Второй способ. Заметим, что сумма «крайних» корней уравнения (х — 1)(х + 1)(х + 3)(ж + 5) = 0 равна сумме «средних» корней: -5 + 1 = -3 — 1 = -4. Поэтому соответствующие произведения
    (x — 1)(x + 5) = х 2 + 4х — 5 и (х + 1)(х + 3) =x 2 + 4x + 3 имеют одинаковое слагаемое х 2 + 4х. В этом случае удобно сделать замену переменных: t = х 2 + 4х. Тогда заданное уравнение примет вид (t — 5)(t + 3) = 20 t 2 — 2t — 35 = 0 t = 7 и t = — 5.
    В старых переменных имеем: х 2 + 4х = 7 х = — 2 ± √11 , x 2 + 4x = -5 Ø.
    Метод интервалов для рациональных функций.
    1) двучлен (х — а) в нечетной степени ведет себя так же, как (х — а),
    2) двучлен (х — а) в четной степени ведет себя по-другому: он не меняет знак при переходе через точку а.
    3) квадратный трехчлен, имеющий положительный коэффициент при х 2 и отрицательный дискриминант, всегда положителен и может быть опущен при решении любого неравенства.
    4) при переходе через точку a может изменить знак только один множитель, (x — а) k выражение (x — b) n , b ≠ a при переходе через а знак не меняет.
    Уравнения вида: √f(x) = g(x)
    Обратим внимание на то, что при этом ОДЗ выполняется автоматически и его можно не писать, а условие g(x) ≥ 0 необходимо проверять.
    Уравнения вида: √f(x) = √g(x)
    При таком способе решения достаточно проверить неотрицательность одной из функций — можно выбрать более простую.
    Неравенство вида: √f(x) / g(x)≤ 0 (или ≥ 0)
    школьники очень часто ошибаются. Воспользуемся определением нестрогого неравенства (для определенности будем рассматривать один знак, например≥)
    Неравенство вида: √f(x) > g(x) (или g(x) выполнено в ОДЗ, а неравенство √f(x) f(x) — g 2 (x) ≤ (≥) 0.
    Отсюда следует правило
    Правило 1. Если g(х) ≥ 0, то знак разности √f(x) — g(x)совпадает со знаком разности f(x) — g 2 (x) в ОДЗ.
    Отсюда следуют условия равносильности
    44(C2).Решите неравенство √2X 2 — 7X — 4 > -X — 0,25. [МФТИ, 1998]
    □ Найдем сначала ОДЗ:
    2X 2 — 7X — 4 ≥ 0 x € ( — ∞; — 0,5) U [4; + ∞).
    Теперь рассмотрим два случая.
    - Если — х — 0,25 x > — 0,25, то неравенство выполнено в ОДЗ, т. е. X € [4; + ∞).
    - Если — х — 0,25 ≥ 0 х ≤ — 0,25, то
    Объединяя оба случая, получаем окончательный ответ.
    Ответ: ( — ∞; (15 — √2X 2 — 7X — 4 ) / 4) U [4; + ∞).
    Неравенство вида: √f(x) ≤ √g(x)
    Правило 2. Знак разности √f(x) — √g(x) совпадает со знаком разности f(x) — g(x) в ОДЗ.
    Более сложные неравенства
    Т. к. при g(х) ≥ 0 знак разности √f(x) — g(x) совпадает со знаком разности f(x) — g 2 (x) в ОДЗ, то получаются условия равносильности:
    Реферат: Тема: «Рациональные и иррациональные уравнения, неравенства и системы»
    профильного обучения элективного курса
    по алгебре и началам анализа
    Тема: «Рациональные и иррациональные уравнения, неравенства и системы »
    I квалификационной категории
    лицея №2 г. Буинска РТ
    Элективный курс профильного обучения посвящен одному из традиционных разделов элементарной математики: решению рациональных и иррациональных уравнений, неравенств и систем уравнений.
    Задачи такого типа часто предлагаются прямым или косвенным образом в различных заданиях выпускных экзаменов средней школы, в заданиях уровня «А», «В» и «С» на ЕГЭ, и на вступительных экзаменах в ссузы и вузы.
    Раздел элементарной математики рациональные уравнения, неравенства и системы является основополагающим и поэтому исключительно важным. Это обстоятельство обуславливается следующими двумя моментами.
    Во- первых, именно на материале рациональных уравнений, неравенств и систем происходит знакомство школьника с основными понятиями и вырабатывается навык обращения с ними.
    Во – вторых, решение задач с других разделов элементарной математики, либо непосредственно либо посредством операции замены сводится именно к решению рациональных уравнений, неравенств и систем.
    Этот курс ставит своей целью на специально подобранном материале выработать умения и навыки, научиться применять основные методы рассуждений и технические приемы, наиболее часто встречающиеся при решении рациональных и иррациональных уравнений, неравенств и систем.
    При подборе материала этого курса учитывалась экзаменационная практика прошлых лет, заданий ЕГЭ.
    Помимо общетеоретических сведений и разнообразных задач в данный курс включены и задачи для самостоятельного решения, работа над которыми будет способствовать лучшему усвоению материала и закреплению приобретенных технических навыков.
    Предлагаемый курс освещает намеченные, но совершенно не проработанные в общем курсе школьной математики вопросы. Стоит отметить, что навыки в применении этих подходов совершенно необходимы каждому ученику, желающему хорошо подготовиться для успешной сдачи конкурсных экзаменов, а также будет хорошим подспорьем для успешных выступлений на математических олимпиадах. Познавательный материал курса будет способствовать не только выработке умений и закреплению навыков, но и формированию устойчивого интереса учащихся к процессу и содержанию деятельности, а также познавательной и социальной активности.
    Данный курс предусматривает формирование устойчивого интереса к предмету, выявление и развитие математических способностей, ориентацию на профессии, существенным образом связанные с математикой, выбору профиля дальнейшего обучения.
    Данный курс рассчитан на 34 часа, предполагает компактное и четкое изложение теории вопроса, решение типовых задач, самостоятельную работу.
    Предлагаемые задачи различны по уровню сложности: от простых упражнений на применение изученных формул до достаточно трудных заданий. Каждое занятие состоит из двух частей: задачи, решаемые с учителем, и задачи для самостоятельного (или домашнего) решения. Основные формы организации учебных занятий: лекция, объяснение, практическая работа, семинар. Разнообразный дидактический материал дает возможность отбирать дополнительные задания для учащихся разной степени подготовки: уровень сложности задач варьируется от простых до конкурсных и олимпиадных. Все занятия направлены на развитие интереса школьников к предмету, на расширение представлений об изучаемом материале, на решение новых и интересных задач.
    Курс является открытым. В него можно добавлять новые фрагменты, развивать тематику или заменять какие- либо разделы другими. Главное, чтобы они были небольшими по объему, интересными для учащихся, соответствовали их возможностям. Программа мобильна, т.е. дает возможность уменьшить количество задач по данной теме. (так как многие задания предназначены на отработку навыков по одному типу задач) при установлении степени достижения результатов.
    Программа может быть эффективно использована в 10-11 классах с любой степенью подготовленности, способствует развитию познавательных интересов, мышления учащихся, предоставляет возможность подготовиться к сознательному выбору профиля обучения и дальнейшей специализации.
    Для учащихся, которые пока не проявляют заметной склонности к математике, эти занятия могут стать толчком в развитии интереса к предмету и вызвать желание узнать больше. Хотя при изучении курса не ставится цель выработки каких- либо специальных умений и навыков, при достаточно полном рассмотрении вопросов курса, несомненно, появится прогресс в подготовке учащихся.
    Выработать умения и навыки решать рациональные и иррациональные уравнения, неравенства и системы.
    Восполнить некоторые содержательные пробелы основного курса, придающие ему необходимую целостность.
    Показать некоторые нестандартные приемы решения задач.
    Рассмотреть основные методы, способы, приемы и подходы решения рациональных уравнений, неравенств и систем.
    Научить различать, видеть основные приемы, подходы решения рациональных и иррациональных уравнений, неравенств и систем и применять их в традиционных и нетрадиционных примерах и задачах.
    Развивать у учащихся интерес к решению рациональных, иррациональных уравнений, неравенств и систем неравенств, видеть красоту решения этих примеров.
    Формировать качества мышления, характерные для математической деятельности и необходимые человеку для жизни в современном обществе.
    Помочь осознать ученику степень значимости своего интереса к математике и оценить свои возможности.
    Воспитывать чувство уверенности в себе, чувства удовлетворенности от приложенного труда.
    — Научить учащихся решать задачи более высокой, по сравнению с обязательным уровнем , сложности.
    -Овладеть рядом математических умений на уровне свободного их использования.
    -Помочь ученику оценить свой потенциал с точки зрения образовательной перспективы.
    ^ Учебно- тематический план
    Раздел 1. Рациональные уравнения
    §2 Метод разложения на множители
    ^ Раздел 2. Рациональные неравенства
    Раздел 3. Система рациональных уравнений.
    §1. Однородные системы.
    §2 Симметрические системы.
    §3 Искусственные методы.
    Раздел 4.Уравнения, неравенства и
    системы уравнений, содержащие
    неизвестное под знаком модуля.
    §1 Метод раскрытия модулей.
    §2 Некоторые частные приемы решения уравнений и неравенств с модулями.
    Иррациональные уравнения и неравенства.
    Использование тригонометрических замен
    Тема. Рациональные уравнения.(7часов)
    Метод замены. Метод разложения на множители.
    Актуализируются знания по методу замены, по методу разложения на множители, формулы, вводятся новые подходы решения уравнении.
    ^ Методы обучения: беседа. Лекция. Объяснение.
    Формы обучения: фронтальная работа, индивидуальная, разноуровневая.
    Форма контроля: проверка индивидуальной домашней самостоятельной работы, решение текстовых заданий, самостоятельная работа.
    Тема. Рациональные неравенства (4 часа)
    Актуализируются прежние знания, рассматриваются новые подходы , приемы и их использование при решении задач. Формирование умений решать рациональные неравенства.
    ^ Методы обучения: лекция, беседа.
    Формы обучения: индивидуальные домашние задания, дифференцированная (разноуровневая) работа.
    Форма контроля: проверка самостоятельных работ, текстовых заданий.
    Тема. Системы рациональных уравнений.(8 часов)
    Актуализация прежних знаний, рассмотреть подходы решения однородных систем, симметрических систем, искусственных систем. Формирование умений решения систем уравнений.
    ^ Методы обучения: лекция, беседа, объяснение.
    Формы обучения: групповая работа, индивидуальная, решение тренировочных упражнений.
    Методы контроля: проверка дифференцированной самостоятельной работы.
    Тема. Уравнения, неравенства и системы, содержащие неизвестное под знаком модуля. (6 часов)
    Рассмотреть подходы, методы, приемы решения уравнений, неравенств и систем уравнений, содержащих неизвестное под знаком модуля. Решение заданий такого характера.
    ^ Методы обучения: лекция, объяснение.
    Формы обучения: фронтальная, индивидуальная, разноуровневая работа.
    Формы контроля: защита проектов.
    Тема. Иррациональные уравнения и неравенства.(4 часа)
    Актуализация имеющихся знаний, рассмотрение новых приемов решения иррациональных уравнений и неравенств.
    ^ Методы обучения: лекция, объяснение, беседа.
    Формы обучения: фронтальная работа, индивидуальная работа, решение тренировочных задач.
    Форма контроля: защита рефератов, проверка самостоятельных работ.
    Тема. Использование тригонометрических замен.(2 часа)
    Познакомить учащихся с методом использования тригонометрических замен. Формирование умений и навыков применять такие замены.
    ^ Формы обучения: лекция, объяснение.
    Методы обучения: решение тренировочных упражнений, индивидуальная работа, фронтальная работа.
    Формы контроля: проверка домашней контрольной работы, самостоятельной работы.
    Заключительный урок(2 часа)- обобщение либо в виде защиты проектов по одной теме, либо групповая защита проектов по всему курсу.
    Вводится понятие рациональной функции, которое понадобится в этом и следующем разделах. Рациональной функцией от аргумента х называется такая функция, аналитическое выражение которой строится из х и констант с помощью операций арифметики (сложение, вычитание, умножение, деление) и операции возведения в натуральную степень. Согласно другому, но эквивалентному приведенному, варианту определения, рациональной называется такая функция, которая представима в виде отношения двух многочленов. Рациональным уравнением называется такое уравнение, у которого и левая, и правая части являются рациональными функциями. Здесь также возможен эквивалентный вариант, а именно: рациональным называется уравнение вида R(x) =0, где R(x) – рациональная функция. Легко усматривается, что решение рационального уравнения сводится к решению уравнений вида P(x)=0, где P(x)- некоторый многочлен. Если при этом степень многочлена Р(х) не превышает двух, то уравнение решается стандартными средствами, поскольку является либо линейными, либо квадратным. Если же степень многочлена Р(х) больше двух, то решение означенного уравнения требует специальных приемов.
    Биквадратные уравнения ах4 +bх2 +с=0 Делая замену t= x2 можно переписать исходное уравнение в виде квадратного уравнения at2 +bt+c=0, найти его решение (если, конечно, они существуют), а уже затем восстановить, исходя из найденных значений t, искомые решения х исходного уравнения. Решение уравнений.
    ^ Решение возвратного уравнения. Возвратное (симметричное) уравнение, отличительной особенностью которого является равенство коэффициентов, равностоящих от концов стоящей в левой части уравнения многочлена.
    ^ Однородные уравнения. Уравнения вида au+ bv =0 называется однородным уравнением первой степени, au2 + buv + cv2 =0 называется однородным уравнением второй степени, au3+ bu2 v + cuv2+ dv3 =0 называется однородным уравнением третьей степени относительно u и v и так далее. Поделив обе части однородного уравнения k- ой степени на vk, мы получим уравнение с одним неизвестным y= u/ v . При этом, разумеется. Отдельно должен быть рассмотрен случай, когда v= 0. Рассматривается уравнение, сводящееся к однородному.
    §2. Метод разложения на множители.
    Рассматриваются уравнения вида Р(x) =0, где Р(x) – многочлен с целыми коэффициентами, и решать их, раскладывая многочлен Р(x) на множители. Процедура этого разложения основывается на следующих двух утверждениях.
    Утверждение 1. Пусть несократимая дробь p/q является корнем многочлена anxn+ an-1 x n-1 + …+ a1 x + a 0 с целыми коэффициентами an, an-1, …+ a1 + a 0. Тогда аnделится на q, а а 0 делится на p.
    Утверждение 2. Пусть несократимая дробь p/q является корнем многочлена Р(x) с целыми коэффициентами. Тогда Р(x)= (qx- p) Q(x), где Q(x)- также многочлен с целыми коэффициентами, причем его степень на единицу меньше степени многочлена Р(x).
    Особенно важным в практическом отношении является случай. Когда многочлен Р(x) имеет приведенную форму, то есть когда a n=1.
    В применении к таким (приведенным) многочленам сформулированные выше утверждения 1 и 2 преобразуются в
    Утверждение 3. Пусть целое число х0 является корнем приведенного многочлена с целыми коэффициентами. Тогда свободный член этого многочлена делится на х0.
    Утверждение 4. Пусть х0- целый корень приведенного многочлена Р(х) с целыми коэффициентами. Тогда Р(х) = (х- х0) Q(x), где Q(x) – также многочлен с целыми коэффициентами, причем его степень на единицу меньше степени многочлена Р(х)
    Практическое использование утверждений 3 и 4 в применении к приведенному многочлену Р(х) с целыми коэффициентами состоит в следующем. Сначала составляется список всех целых делителей свободного члена многочлена Р(х). Входящие в этот список числа последовательно проверяются (непосредственной подстановкой в Р(х)) до момента нахождения числа х0 ,являющегося корнем многочлена Р(х). После этого входящие в Р (х) слагаемые группируются таким образом, чтобы реализовать разложение Р(х)= (х-х0) Q(x). Примеры решения задач.
    Используя введенное в разделе 1 понятие рациональной функции, можно определить рациональное неравенство как неравенство, правая и левая части которого являются рациональными функциями. По- другому рациональное неравенство можно определить как неравенство, имеющее один из следующих видов
    R(x)>0, R(x) . Разложим числитель и знаменатель функции R(x) на множители двух типов: линейные и квадратичные с отрицательным дискриминантом. Отметим, что возможность такого разложения устанавливается в высшей алгебре. Квадратичные множители с отрицательным дискриминантом являются знакоопределенными (не меняют знака), а следовательно знак R(x) полностью зависит от знаков линейных множителей. Очевидно, что корень линейного множителя разделяет числовую ось на два участка, в одном из которых этот множитель знакоположителен, а в другом знакоотрицателен. Поэтому смена знака функции R(x) возможна только при переходе через корень того или иного линейного множителя. Отсюда становится понятной предлагаемая процедура решения рациональных неравенств. Надо нанести на числовую ось все корни линейных множителей, а затем, двигаясь по числовой оси, отмечать знак функции R(x) на различных участках, следя за возможной сменой знака функции R(x) при переходе через корни линейных множителей. Затем, уже определив знаки R(x) на различных участках, следует обратить внимание на то, входят ли граничные точки (точки, которые разделяют участки) в ответ. Решение задач.
    ^ III. Система рациональных уравнений.
    Наиболее распространенным методом решения систем уравнений в школьной практике, например систем двух уравнений с двумя неизвестными, является метод подстановки в простейшей форме, когда, используя одно уравнение системы, выражают какое- либо неизвестное через другое, а затем подставляют найденное выражение в неиспользованное уравнение системы. Результатом таких действий является сведение системы к уравнению. Такой метод хорошо работает, если хотя бы одно из уравнений системы- линейное. В противном случае значительные сложности могут возникнуть уже на первом этапе решения, когда одно неизвестное выражается через другое. В такой ситуации надо применить, как правило, метод замены, выбирая эту замену с учетом особенностей конкретной системы.
    §1. Однородные системы.
    Система двух уравнений с двумя неизвестными называется однородной системой порядка n ( n- натуральное число), если оно имеет вид
    a0 xn+ a1xn-1y+ a2 xn-2y2+……+ anyn= c
    b0 xn+ b1xn-1y+ b2 xn-2y2+……+ bnyn= d
    Однородные системы решают следующим способом. Из первого уравнения , предварительно умноженного на d, вычитают второе уравнение, предварительно умноженное на c. В результате получается однородное уравнение, описанное в конце раздела §1 раздела 1 (Литература№1). Используя описанную там методику, можно из полученного уравнений найти отношение y/x, что откроет путь к решению всей системы, поскольку появится возможность простого выражения одного неизвестного через другое и последующей подстановки. Решение систем.
    §2 Симметрические системы.
    Метод решения симметрических систем основан на том. Что симметрические многочлены переменных х, у могут быть выражены через симметрические многочлены х+у и ху, называемые основными. В связи с этим оказывается весьма эффективной замена u=x+y, v=xy, существенно упрощающая систему. Решение примеров.
    §3 Искусственные методы.
    В двух предыдущих параграфах данного раздела были описаны методы решения рациональных систем, имеющие алгоритмический характер. Но эти методы не являются универсальными, и некоторые системы им не поддаются. В этой ситуации следует искать способ такого преобразования исходной системы, который привел бы ее к виду, допускающему применение стандартных методов решения. При решении той или иной конкретной системы приходится это преобразование находить методом проб и ошибок. Но ошибок можно сделать существенно меньше, если предварительно ознакомиться и сохранить в памяти хотя бы несколько различных примеров упомянутых преобразований. Разобрав задачи данного типа, учащиеся выработают интуицию в нахождении мотивов эффективных преобразований различных систем. Решение математических уравнений.
    ^ IV. Уравнения, неравенства и системы уравнений, содержащие неизвестное под знаком модуля.
    Два основных метода решения уравнений. Неравенств и систем уравнений, содержащих неизвестное под знаком модуля. Первый метод основан на избавлении от модулей согласно их определению. Второй метод основан на избавлении от модулей посредством операции возвышения уравнения или неравенства в квадрат и перехода к системе.
    §1 Метод раскрытия модулей.
    Пусть нам предстоит решить уравнение, содержащее неизвестное под знаком модуля. Разобьем числовую прямую на участки знакопостоянства подмодульного выражения и на каждом из этих участков раскроем модуль согласно определению. В результате таких действий исходное уравнение преобразуется в уравнение, уже не содержащее модуля. Решим его и запишем в ответ найденные решения, если они входят в рассматриваемый на данном этапе участок. Проделав эту процедуру для каждого из возникающих участков, получим окончательный ответ. Решение примеров.
    Решение системы с модулями осуществляется в точности таким же способом, как решение уравнений с модулями. Однако при этом возможна ситуация, когда система вырождается в уравнение, и тогда возникают некоторые технологические трудности при формировании ответа. Решение примеров.
    § 2 Некоторые частные приемы решения уравнений и неравенств с модулями.
    Рассмотренная в §1 методика решения уравнений. Неравенств и систем с модулями является универсальной, но приводящей иногда к необходимости утомительного рассмотрения многочисленных случаев. Поэтому к ней следует обращаться тогда, когда более простые приемы, основанные на конкретных особенностях рассматриваемой задачи, не срабатывают. Более простые приемы- это приемы, использующие для устранения модулей операцию возвышения в квадрат и сведения рассматриваемого уравнения или неравенства к системе уравнений или неравенств, уже не содержащих модули. Решение примеров.
    ^ Иррациональные уравнения и неравенства.
    Основным методом решения иррациональных уравнений и неравенств является метод освобождения от радикалов, использующий для этого процедуру возвышения обеих частей уравнения или неравенства в ту или иную степень. Эта процедура нарушает требования равносильных преобразований уравнения или неравенства, поэтому поговорим об этом подробнее.
    При возвышении уравнения в квадрат (это наиболее часто встречающийся случай) мы получаем так называемое следствие, то есть уравнение, сохранившее все корни исходного уравнения, но приобретшее, быть может, посторонние корни, не являющиеся корнями исходного уравнения. Поэтому, если мы применяем процедуру возвышения уравнения в квадрат, без каких- либо ограничений и оговорок, то обязаны проверить найденные, в конце концов, решения полученного следствия подстановкой в исходное уравнение.
    Если мы возвышаем в квадрат уравнение, обе части которого определены и неотрицательны на некотором множестве, то возведенное в квадрат уравнение равносильно исходному на упомянутом множестве. То же самое может быть сказано применительно к процедуре возвышения в квадрат неравенств.
    Основным элементом решения иррационального неравенства является возведение его на том или ином этапе решения в квадрат. К этой операции следует готовиться, добиваясь того, чтобы знаки левой и правой частей подлежащего возвышению в квадрат неравенства были определены на участках их знакопостоянства. Если обе части неравенства неотрицательны, операция возвышения в квадрат допустима, то есть приводит к равносильному неравенству. Решение примеров.
    ^ VI. Использование тригонометрических замен.
    VII. Защита рефератов, проектов по одному из разделов по всему курсу
    Данный элективный курс «Рациональные и иррациональные уравнения, неравенства и системы » задает примерный объем знаний, умений и навыков, которыми должны овладеть школьники. Сюда входят знания, умения и навыки, обязательное приобретение которых предусматривает программа общеобразовательной школы: однако предполагается более высокое качество их сформированности. Учащиеся должны научиться решать задачи более высокой, по сравнению с обязательным уровнем сложности, овладеть рядом технических и интеллектуальных умений на уровне их свободного использования. Следует отметить, что требования к знаниям и умениям ни в коем случае не должны быть завышены, чрезмерность требований порождает перегрузку и ведет к угасанию интереса. Одна из целей преподавания данного курса- помочь осознать ученику степень значимости своего интереса к математике и оценить свои возможности. Поэтому интерес и склонность учащегося к занятиям на курсах должны всемерно подкрепляться.
    На уроках можно использовать фронтальный опрос, который охватывает большую часть учащихся класса. Эта форма работы развивает точную, лаконичную речь, способность работать в скором темпе, быстро собираться с мыслями и принимать решения.
    Поурочные домашние задания являются обязательными для всех. Активным учащимся можно давать задания из дополнительной части. Проверка заданий для самостоятельного решения осуществляется на занятии путем узнавания способа действий и называния ответа.
    В результате изучения курса учащиеся должны уметь:
    уверенно решать простейшие рациональные, иррациональные уравнения, неравенства и системы уравнений;
    применять изученные приемы и способы решения на практике при самостоятельном решении заданий из ЕГЭ;
    уверенно владеть системой определений и алгоритмов;
    решать традиционные и нетрадиционные задания , а также задания из ЕГЭ.
    ^ Возможные критерии оценок.
    Критерии при выставлении оценок могут быть следующие.
    Оценка «отлично»(5)- учащийся демонстрирует сознательное и ответственное отношение, сопровождающееся ярко выраженным интересом к учению; учащийся усвоил теоретически материал курса, получил навыки в его применении при решении конкретных задач; в работе над индивидуальными домашними заданиями учащийся продемонстрировал умение работать самостоятельно. Как правило, для получения высокой оценки учащийся должен показать не только знание теории и владение набором стандартных методов, но и известную сообразительность, математическую культуру.
    ^ Оценка «хорошо»(4)- учащийся освоил идеи и методы данного курса в такой степени, что может справиться со стандартными заданиями; выполняет домашние задания прилежно (без проявления явных творческих способностей); наблюдаются определенные положительные результаты, свидетельствующие об интеллектуальном росте и о возрастании общих умений учащегося.
    ^ Оценка «удовлетворительно»(3)- учащийся освоил наиболее простые идеи и методы программы, что позволило ему достаточно успешно выполнять простые задания.
    Оценка «неудовлетворительно» (2)- ученик не проявил ни прилежания, ни заинтересованности в освоении курса, не справляется с решением простых задач.
    ^ Организация и проведение аттестации учеников.
    Целью аттестации по данному элективному курсу является констатация личных достижений учащихся по освоению содержания курса, а также умений и навыков решения рациональных уравнений, иррациональных уравнений, неравенств и систем, а также качественная оценка усвоения материала, самостоятельных работ, рефератов.
    Обсуждение результатов выполнения реферата можно проводить во время публичной защиты, куда могут быть приглашены и не изучавшие данный курс учащиеся. Это может дать не только познавательный, но и мотивационный эффект.
    Литература для учителя.
    1.Илюшкин В.А., Куприн В.Г. Рациональные и иррациональные уравнения, неравенства и системы (метод решения конкурсных задач)
    2. Гараев К.Г., Исхаков Э.М., Мубаракзянов Г.М. Математика.
    Издательство «Магариф», Казань, 1998 г.
    3.Задания из ЕГЭ.
    4.Журнал «Математика в школе», №6, 1998 г.
    5. Шарыгин Н.Ф. Математика для поступающих в вузы.-
    Издательство «Дрофа» Москва 1995 г.
    6. Под редакцией М.И. Сканави, Решение конкурсных задач по математике.- Москва ТО «Сашко», 1995 г.
    7.«Математика» Вступительные испытания ЕГЭ- 2008 под редакцией Лысенко Ф.Ф.. Издательство «Легион» Ростов на Дону, 2007 г.
    8.ЧеркасовО.Ю., Якушев А.Г. Математика: интенсивный курс подготовки к экзамену.- 3-е изд., испр. И дополн.- М.: Рольф,Айрис- пресс,1998
    9. Шабунин М.И. Пособие по математике для поступающих в вузы.- М: Лаборатория базовых знаний, 1999
    3. Звавич Л.И.,Шляпочник Л.Я.,Чинкина М.В.,Алгебра и начала анализа 8-10 кл.: пособие для школ с углубленным изучением математики. –
    11. Под редакцией Лысенко Ф.Ф. Математика. Вступительные испытания ЕГЭ- 2008.- Издательство «Легион» Ростов на Дону, 2007 г.
    Литература для учащихся.
    1. Текстовые задачи из заданий ЕГЭ и заданий вступительных экзаменов.
    2. Решение задач и выполнение заданий с комментариями, ответами для подготовки к единому государственному экзамену: в 2 ч.- / сост. В.Н.Студенецкая, З.С.Гребнева- Волгоград: Учитель,2003.
    3.Перельман Я.И. Занимательная алгебра.- М., 1967
    4. Шарыгин Н.Ф. Математика для поступающих в вуз.-
    5.Сканави М.И. Решение конкурсных задач по математике.-
    М.: ТО «Сашко», 1995
    6. Свечников А.А. Путешествие в историю математики, или как люди научились считать: книга для тех, кто учит и учится.- М.: Педагогика- Пресс, 1995.
    7. Под редакцией Лысенко Ф.Ф. Математика. Вступительные испытания ЕГЭ- 2008.- Издательство «Легион» Ростов на Дону, 2007 г.
    
    источники:
    http://student.zoomru.ru/math/racionalnye-i-irracionalnye-uravneniya-i/235100.1833557.s1.html
    http://ronl.org/referaty/raznoe/527536/