Регрессионные модели с одним уравнением

5 видов регрессии и их свойства

Линейная и логистическая регрессии обычно являются первыми видами регрессии, которые изучают в таких областях, как машинное обучение и наука о данных. Оба метода считаются эффективными, так как их легко понять и использовать. Однако, такая простота также имеет несколько недостатков, и во многих случаях лучше выбирать другую регрессионную модель. Существует множество видов регрессии, каждый из которых имеет свои достоинства и недостатки.

Мы познакомимся с 7 наиболее распространенными алгоритмами регрессии и опишем их свойства. Также мы узнаем, в каких ситуация и с какими видами данных лучше использовать тот или иной алгоритм. В конце мы расскажем о некоторых инструментах для построения регрессии и поможем лучше разобраться в регрессионных моделях в целом!

Линейная регрессия

Регрессия — это метод, используемый для моделирования и анализа отношений между переменными, а также для того, чтобы увидеть, как эти переменные вместе влияют на получение определенного результата. Линейная регрессия относится к такому виду регрессионной модели, который состоит из взаимосвязанных переменных. Начнем с простого. Парная (простая) линейная регрессия — это модель, позволяющая моделировать взаимосвязь между значениями одной входной независимой и одной выходной зависимой переменными с помощью линейной модели, например, прямой.

Более распространенной моделью является множественная линейная регрессия, которая предполагает установление линейной зависимости между множеством входных независимых и одной выходной зависимой переменных. Такая модель остается линейной по той причине, что выход является линейной комбинацией входных переменных. Мы можем построить модель множественной линейной регрессии следующим образом:

Y = a_1*X_1 + a_2*X_2 + a_3*X_3 ……. a_n*X_n + b

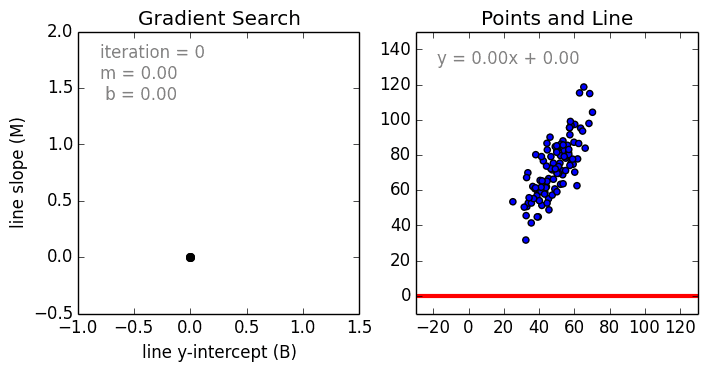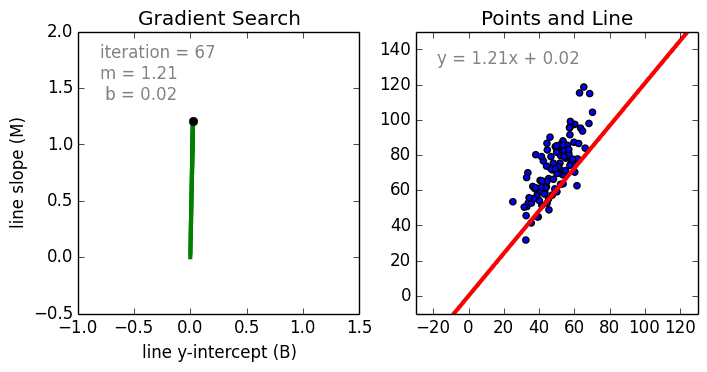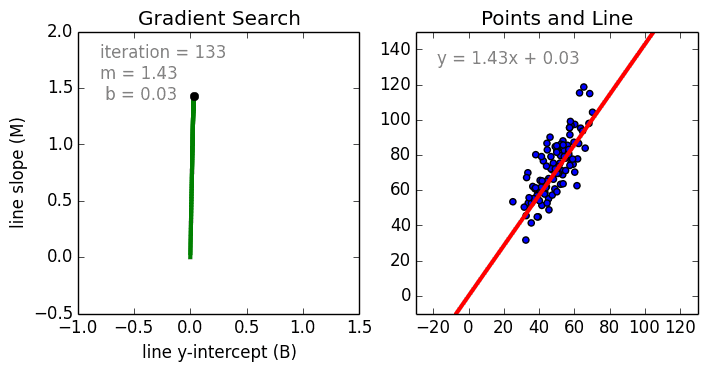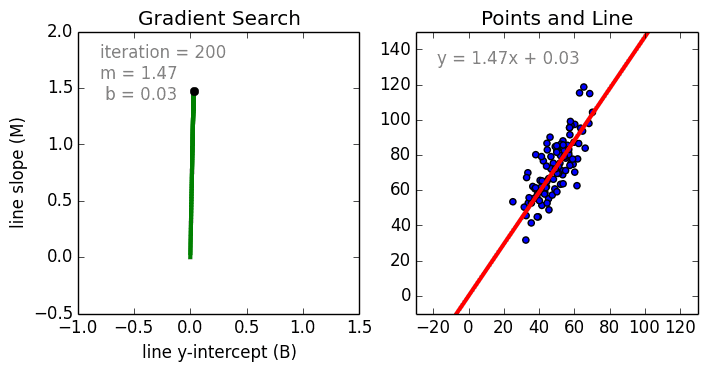
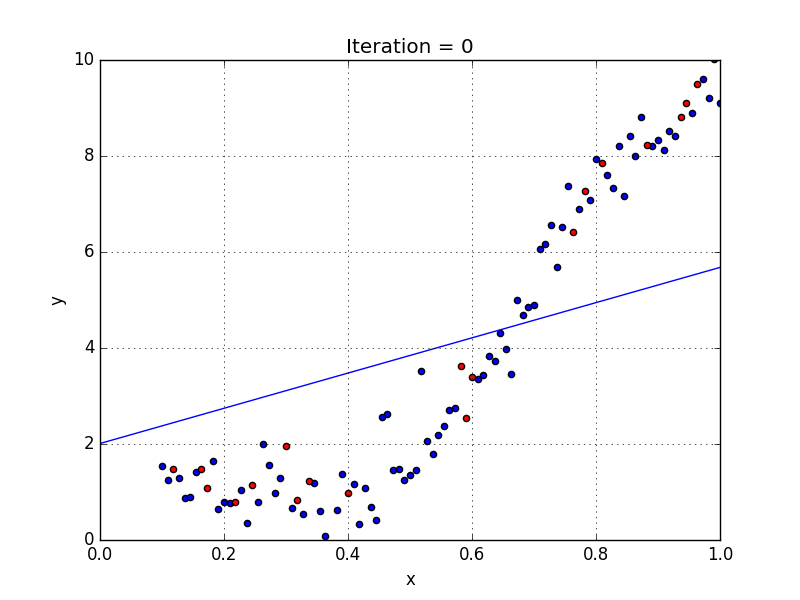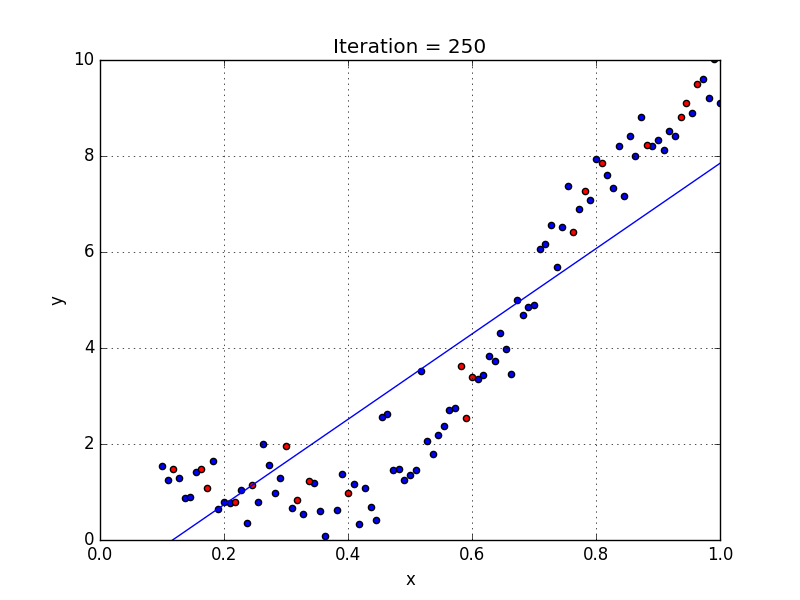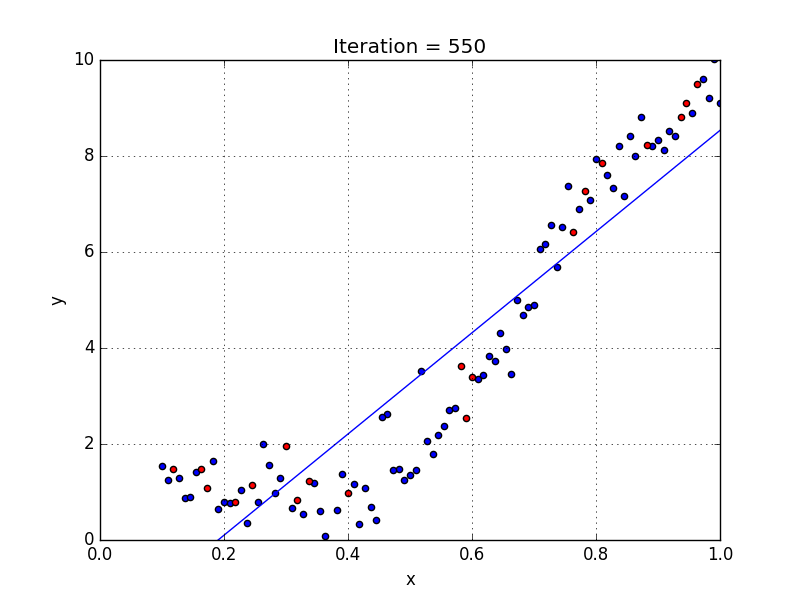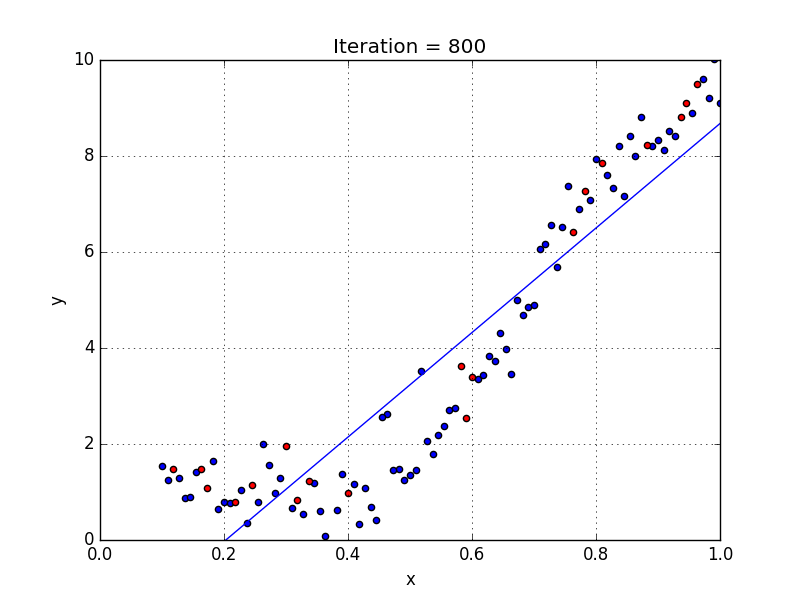
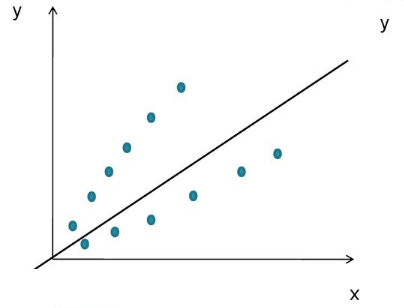
Где a_n — это коэффициенты, X_n — переменные и b — смещение . Как видим, данная функция не содержит нелинейных коэффициентов и, таким образом, подходит только для моделирования линейных сепарабельных данных. Все очень просто: мы взвешиваем значение каждой переменной X_n с помощью весового коэффициента a_n. Данные весовые коэффициенты a_n, а также смещение b вычисляются с применением стохастического градиентного спуска. Посмотрите на график ниже в качестве иллюстрации!

Несколько важных пунктов о линейной регрессии:

• Она легко моделируется и является особенно полезной при создании не очень сложной зависимости, а также при небольшом количестве данных.
• Обозначения интуитивно-понятны.
• Чувствительна к выбросам.

Полиномиальная регрессия

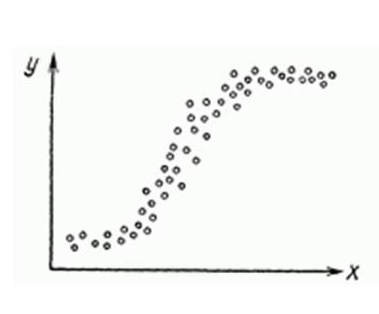
Для создания такой модели, которая подойдет для нелинейно разделяемых данных, можно использовать полиномиальную регрессию. В данном методе проводится кривая линия, зависимая от точек плоскости. В полиномиальной регрессии степень некоторых независимых переменных превышает 1. Например, получится что-то подобное:

Y = a_1*X_1 + (a_2)²*X_2 + (a_3)⁴*X_3 ……. a_n*X_n + b

У некоторых переменных есть степень, у других — нет. Также можно выбрать определенную степень для каждой переменной, но для этого необходимы определенные знания о том, как входные данные связаны с выходными. Сравните линейную и полиномиальную регрессии ниже.

Несколько важных пунктов о полиномиальной регрессии:

• Моделирует нелинейно разделенные данные (чего не может линейная регрессия). Она более гибкая и может моделировать сложные взаимосвязи.
• Полный контроль над моделированием переменных объекта (выбор степени).
• Необходимо внимательно создавать модель. Необходимо обладать некоторыми знаниями о данных, для выбора наиболее подходящей степени.
• При неправильном выборе степени, данная модель может быть перенасыщена.

Гребневая (ридж) регрессия

В случае высокой коллинеарности переменных стандартная линейная и полиномиальная регрессии становятся неэффективными. Коллинеарность — это отношение независимых переменных, близкое к линейному. Наличие высокой коллинеарности можно определить несколькими путями:

• Коэффициент регрессии не важен, несмотря на то, что, теоретически, переменная должна иметь высокую корреляцию с Y.
• При добавлении или удалении переменной из матрицы X, коэффициент регрессии сильно изменяется.
• Переменные матрицы X имеют высокие попарные корреляции (посмотрите корреляционную матрицу).

Сначала можно посмотреть на функцию оптимизации стандартной линейной регрессии для лучшего понимания того, как может помочь гребневая регрессия:

Где X — это матрица переменных, w — веса, y — достоверные данные. Гребневая регрессия — это корректирующая мера для снижения коллинеарности среди предикторных переменных в регрессионной модели. Коллинеарность — это явление, в котором одна переменная во множественной регрессионной модели может быть предсказано линейно, исходя из остальных свойств со значительной степенью точности. Таким образом, из-за высокой корреляции переменных, конечная регрессионная модель сведена к минимальным пределам приближенного значения, то есть она обладает высокой дисперсией.

Гребневая регрессия добавляет небольшой фактор квадратичного смещения для уменьшения дисперсии:

min || Xw — y ||² + z|| w ||²

Такой фактор смещения выводит коэффициенты переменных из строгих ограничений, вводя в модель небольшое смещение, но при этом значительно снижая дисперсию.

Несколько важных пунктов о гребневой регрессии:

• Допущения данной регрессии такие же, как и в методе наименьших квадратов, кроме того факта, что нормальное распределение в гребневой регрессии не предполагается.
• Это уменьшает значение коэффициентов, оставляя их ненулевыми, что предполагает отсутствие отбора признаков.

Регрессия по методу «лассо»

В регрессии лассо, как и в гребневой, мы добавляем условие смещения в функцию оптимизации для того, чтобы уменьшить коллинеарность и, следовательно, дисперсию модели. Но вместо квадратичного смещения, мы используем смещение абсолютного значения:

min || Xw — y ||² + z|| w ||

Существует несколько различий между гребневой регрессией и лассо, которые восстанавливают различия в свойствах регуляризаций L2 и L1:

• Встроенный отбор признаков — считается полезным свойством, которое есть в норме L1, но отсутствует в норме L2. Отбор признаков является результатом нормы L1, которая производит разреженные коэффициенты. Например, предположим, что модель имеет 100 коэффициентов, но лишь 10 из них имеют коэффициенты отличные от нуля. Соответственно, «остальные 90 предикторов являются бесполезными в прогнозировании искомого значения». Норма L2 производит неразряженные коэффициенты и не может производить отбор признаков. Таким образом, можно сказать, что регрессия лассо производит «выбор параметров», так как не выбранные переменные будут иметь общий вес, равный 0.
• Разряженность означает, что незначительное количество входных данных в матрице (или векторе) имеют значение, отличное от нуля. Норма L1 производит большое количество коэффициентов с нулевым значением или очень малые значения с некоторыми большими коэффициентами. Это связано с предыдущим пунктом, в котором указано, что лассо исполняет выбор свойств.
• Вычислительная эффективность: норма L1 не имеет аналитического решения в отличие от нормы L2. Это позволяет эффективно вычислять решения нормы L2. Однако, решения нормы L1 не обладают свойствами разряженности, что позволяет использовать их с разряженными алгоритмами для более эффективных вычислений.

Регрессия «эластичная сеть»

Эластичная сеть — это гибрид методов регрессии лассо и гребневой регрессии. Она использует как L1, так и L2 регуляризации, учитывая эффективность обоих методов.

min || Xw — y ||² + z_1|| w || + z_2|| w ||²

Практическим преимуществом использования регрессии лассо и гребневой регрессии является то, что это позволяет эластичной сети наследовать некоторую стабильность гребневой регрессии при вращении.

Несколько важных пунктов о регрессии эластичной сети:

• Она создает условия для группового эффекта при высокой корреляции переменных, а не обнуляет некоторые из них, как метод лассо.
• Нет ограничений по количеству выбранных переменных.

Вывод

Вот и все! 5 распространенных видов регрессии и их свойства. Все данные методы регуляризации регрессии (лассо, гребневая и эластичной сети) хорошо функционирует при высокой размерности и мультиколлинеарности среди переменных в наборе данных.

21. Определение эконометрики, используемые мотоды, модели, типы данных.

Р. Фриш ввел название ЭМ определил ЭМ: «эконометрика представляет собой синтез политической экономии, математики и статистики». Другое определение польский экономист Оскар Ланге: «ЭМ — наука, занимающаяся определением при помощи статистических методов конкретных количественных закономерностей, наблюдаемых в экономической жизни».

ЭМ — это наука, связанная с эмпирическим выводом экономических законов.

Классификация моделей и типы данных. На основе экономической теории модель сначала формулируется, затем оцениваются неизвестные параметры (на эмпирических данных), дается прогноз, оценивается точность, прогноза и вырабатываются рекомендации по экономической политике. Можно выделить 3 основных класса моделей, применяемых для анализа и прогноза.

1) Модели временных рядов . К этому классу относятся:

а) модели тренда y ( t ) = T ( t ) + t где T ( t ) — временной тренд заданного параметрического вида (например, линейный T ( t ) = a + b ( t )), t — случайная (стохастическая) компонента.

б) модель сезонности y ( t )= S ( t )+ t ,где S ( t )-периодическая (сезонная) компонента, t — случайная компонента.

в) тренд-сезонные модели

— аддитивная модель y ( t ) = T ( t ) + S ( t ) + t

— мультипликативная модель y(t) = T(t) *S(t) + t

Общая черта моделей врем рядов: они объясняют поведение временного ряда, исходя только из его предыдущих значений.

2)Регрессионные модели с одним уравнением. В таких моделях зависимая (объясняемая) переменная у представляется в виде функций независимых переменных x и β, и случайной составляющей .

y = f(x, β)+ . f(x, β) – не случайная часть.

где х=( x 1, x 2, …, xn )-вектор регрессоров, независимые, объясняемые компоненты.

β = ( β1, β2, …, β n )-вектор параметров.

Простейшее регрессионное уравнение y=β1 x 1+β2 x 2+…+β nx n+, -случайная переменная/компонента.

В зависимости от вида этой функции модели делятся на линейные и нелинейные. И от количества переменных парные и множественные.

3) Системы одновременных уравнений. Эти модели описываются системами уравнений, которые могут состоять из тождеств и регрессионных уравнений, каждое из которых может, кроме объясняющих переменных, включать в себя также объясняемые переменные из других уравнений системы. Таким образом, имеем набор объясняемых переменных, связанных через уравнения системы.

Пример. Модель равновесия.

— функция предложения. Совокупное предложение в момент времени t .

— функция спроса, или спрос на товар в момент времени t . Yt — доход в момент времени t . α – параметры, P — объясняющая переменная. — случайная компонента.

При моделировании экономических процессов встречаются с несколькими типами данных : пространственные данные, временные (динамические) ряды и панельные данные. Пространственные данные — набор сведений (объем производства, количество работников, доход и пр.) по разным экономическим объектам, зафиксированные в один и тот же момент времени (пространственный срез); данные по курсам покупки/продажи наличной валюты в какой-то день по обменным пунктам в Ростове. Временные ряды : ежеквартальные данные по инфляции, ежедневный курс доллара США, котировки акций за последние годы и т.д. Отличительной чертой врем данных — они естественным образом упорядочены по времени и наблюдения в близкие моменты времени часто бывают зависимыми. Панельные данные — это сведения, получаемые в различные моменты времени при наблюдении за одной и той же выборочной совокупностью объектов.

22. Модель парной регрессии. Условия нормальной линейной регрессии (Гаусса-Маркова).

Задачу определения парной регрессии можно сформулировать так: по наблюденным значениям одной переменной ( X ) нужно оценить или предсказать ожидаемое значение другой переменной( Y ). В модели линейной регрессии теоретически предполагается существование между переменными X и Y связи след вида:

Простейшая регрессионная модель: y = + β x + U (1)

y — зависимая, объясняемая переменная, результирующий признак;

х — независимая, объясняющая переменная, регрессор, факторный признак;

U – остаточная компонента; случайный член

, β — неизвестные параметры

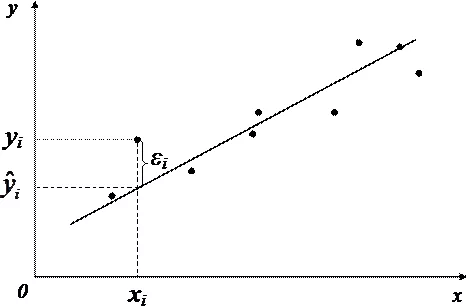
Q1=(x1; ŷ1) ŷ1 = a + bx1 U1 = y1 — ŷ1.

P 1, P 2, P 3, P 4– фактические, наблюдаемые (реальные) значения переменных X , Y

Q 1, Q 2, Q 3, Q 4 – значения переменных в отсутствие случайного члена

Уравнение (1) называется регрессионным уравнением. Мы имеем некоторое число парных наблюдений, характеризующих значения переменных х и у или выборку.

Задача регрессионного анализа состоит в получении оценок неизвестных параметров и β и в определении положения прямой по точкам Р (фактическое значение). Зависимая переменная состоит из неслучайной и случайной составляющих.

Наиболее популярным и простым методом получения оценок неизвестных параметров, является метод наименьших квадратов (МНК). Критерием выбора функции в этом методе, является минимизация суммы квадратов остатков. Остаток – это разница между наблюдаемым значением переменной у и ее теоретическим значением ŷ, при каждом значении объясняющей переменной.

Предположим, что мы нашли эти оценки и можно записать уравнение: ŷ = a + bx , где а — регрессионная постоянная, b – коэффициент регрессии. ŷ — теоретическое значение объясняемой переменной, х- независимая переменная, регрессор.

Чтобы оценки по МНК были наилучшими в классе оценок (несмещенными и эффективными) должны выполняться 4 условия Гаусса-Маркова.

1) Математическое ожидание случайного члена в V наблюдении д.б.=0, т.е E ( ui )=0, V i =1, n

Иногда случайная компонента будет положительной, иногда отрицательной, она не должна иметь систематического смещения ни в одном из 2х возможных направлений. Если уравнение регрессии включает константу a , то можно предположить, что это условие выполняется автоматически, т.к. роль const в определении V систематической тенденции в y , которую не учитывают объясняющие переменные, включенные в уравнение регрессии.

2) гомоскедастичность: дисперсия случайного члена д.б. постоянной для всех наблюдений. Иногда случайная компонента будет больше иногда меньше, но не д.б. априорной причины для того, чтоб случайная компонента порождала большую ошибку в одних наблюдениях, чем в других. Если дисперсия различна-то это гетероскедастичность.

3)Отсутствие автокорреляции случайного члена, т.е систематической связи между значениями случайной компоненты в любом из 2-х наблюдениях. Если случайная компонента велика и положительна в одном направлении это не должно обуславливать систематической тенденции к тому, что она была большой и положительной в след наблюдении.

Значения случайной компоненты д.б. независимы друг от друга выполнение этого условия исключает автокорреляцию ошибок.: E ( ui )= E ( uj )=0 E ( ui , uj )=0, V ij

4)Случайный член д.б. распределен независимо от объясняющих переменных E ( xi , ui )=0,

5*) случайная компонента имеет нормальное распределение ( ).

Если выполняется 4 условия Г-М, то оценки по МНК являются наилучшими в классе линейных оценок. Если выполняется 5 условие, то оценки также будут иметь нормальное распределение.

23. Оценка неизвестных параметров. МНК. Свойства оценок.

Уравнение y = + β x + U называется регрессионным уравнением. Имеем некоторое число пар наблюдений, характеризующих значения переменных х и у или выборку. Нужно оценить параметры этого уравнения и β, т.е. отыскать наилучшие оценки для них.

Пусть мы нашли эти оценки и можем записать уравнение: ŷ = a + bx , где а — регрессионная постоянная, b — коэффициент регрессии, а и b – найдены по МНК. ŷ — теоретическое значение объясняемой переменной.

Используя полученное уравнение, можно рассчитать (как остатки) ei — оценки конкретных значений ошибок u в нашей выборке. Наиболее популярным метод ЭМ-МНК. Он позволяет получить такие оценки параметров и β, при которых сумма квадратов оценок ошибки e2 принимает минимальное значение.

Рассмотрим предполагаемую выборку, размер которой равен n , и предположим, а и b — оценки параметров и β. В соответствии с МНК оценки а и b можно получить из условия минимизации суммы квадратов ошибок e2 . Остаток/отклонение – это разница между наибольшим значением переменной y и её теоретическим значением ŷ i

S=i=1,ne2 =(yi – ŷi)2=(yi-a-bixi)2 min

МНК применяется в тех случаях, когда избранное уравнение линейно относительно своих параметров. Нелинейное уравнение следует линеаризовать.

Для отыскания наименьшего значения какой-либо функции сначала надо найти частные производные I порядка. Затем каждую из них приравнять нулю и разрешить полученную систему уравнений относительно переменных.

Преобразуя, полученное: Коэффициент a и b по МНК вычисляются по формулам.

Мы имеем дело с истинной моделью y =+ x + u , u -случайная компонента, x -неслучайная, ,-истинные параметры. Значение х можно считать заданным, а значение у состоит из случайнойноятего значения какой-либо ф- и неслучайной части. Поэтому найденные оценки a и b будут также состоять из 2х частей: для a +, b +.

Если математическое ожидание оценки равняется соответствующей характеристике генеральной совокупности, то оценка называется несмещенной . Если это не так, то оценка называется смещенной и разница между ее математическими ожиданиями и соответствующей теоретической характеристикой генеральной совокупности называется смещением.

Эффективная оценка — это та, у которой дисперсия минимальна.

Если предел оценки по вероятности равен истинному значению характеристики генеральной совокупности, то эта оценка называется состоятельной . Т.е. состоятельной называется такая оценка, которая дает точное значение для большой выборки независимо от входящих в неё конкретных наблюдений.

Свойства оценок a и b (эффективность, состоятельность, несмещенность) существенным образом зависят от свойств случайной составляющей. Чтоб оценки по МНК были наилучшими в классе оценок (несмещенными и эффективными и состоятельными) должно выполняться 4 условия Гаусса-Маркова.

24. Нелинейная регрессия. Методы линеаризации.

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. Различают 2 класса нелинейных регрессий:

• регрессии, нелинейная относительно включенных в анализ объясняющих переменных, но линейных по оцениваемым параметрам

•регрессии, нелинейные по оцениваемым параметрам. Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут быть следующие функции:

полиномы разных степеней: . Парабола- нелинейная по переменным х, линейная по параметрам a , b . (Пример х- объем выпускаемой продукции, у – затраты. х- заработная плата, у – возраст работника)

равносторонняя гипербола: y = a + b / x +

К нелинейным регрессиям по оцениваемым параметрам относятся функции:

Нелинейная регрессия по включенным переменным определяется, как и в линейной регрессии, МНК, т.к. эти функции линейны по параметрам и в этих функциях не нарушаются предпосылки МНК

Для наглядности можно ввести замену переменных.

Класс регрессий, нелинейных по оцениваемым параметрам, подразделяется на 2 типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейная, то она не может быть сведена к линейной функции. Например, в ЭМ исследованиях при изучении эластичности спроса от цен широко используется степенная функция: , где у — спрашиваемое количество; х — цена; ε — случайная ошибка. К этой функции МНК не может быть применен для оценки параметров.

Данная модель нелинейная относительно оцениваемых параметров. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду: lny = lna + blnx + lnε

Соответственно оценки параметров а и b могут быть найдены МНК.

Если же модель представить в виде , то она становится внутренне нелинейной, ибо ее невозможно превратить в линейный вид. Ее нельзя идентифицировать МНК. 25. Смысл и назначение коэффициента корреляции (линейный коэффициент корреляции, индекс корреляции, коэффициент детерминации).

ŷ = a + bx . Если бы между x и y существовала строгай линейно функциональная зависимость, то расчетные значения ŷ были бы в точности равны фактическим у и разность между ними ŷ– y = 0. На самом деле расчетные значения отклоняются от фактических в силу того, что связь между признаками корреляционная.

В качестве меры тесноты взаимосвязи используется коэффициенты корреляции :

-1 r 1. Чем ближе коэффициенты корреляции по абсолют величине к 1, тем теснее связь между признаками. Если | r | → 0, то связь очень слабая. Близость к 0 коэффициента корреляции не означает отсутствие связи между выбранными функциями вообще. При другой функциональной спецификации (линейная/нелинейная) связь м.б. достаточно тесной. Знак при линейном коэффициенте корреляции указывает на направление связи: прямой зависимости соответствует знак плюс, а обратной зависимости – знак минус.

0 r 0,3 очень слабая связь 0,3 r 0,5 слабая связь

0,5 r 0,7 умеренная средняя 0,7 r 1 сильная связь

r = 1 — функциональная зависимость

Для определения качества подборки линейной функции рассчитывается коэффициент детерминации d= r 2*100%, который показывает насколько вариация y зависит от вариации x .

2общ=2фактор+2остаточ (факторная – объясняется факторами включенными в модель, остаточная- объясняется факторами, не включенными в модель)

r 2= — множественный коэффициент детерминации, показывает долю вариации которая обусловлена влиянием других факторов не включенных в модель.

Дисперсия раскладывается ( yi – )2 = (ŷ- )2+( yi – ŷ i )2

Общая дисперсия, т.е отклонение фактического значений от своего среднего значения вызвана множеством причин. Условно их можно разделить на 2 группы:

1.Факторы, включенные в уравнение регрессии в явном виде.

2.Если х не влияет на y , то линия регрессии || оси 0Х, и ŷ = , r =0 и тогда вся дисперсия y обусловлена другими факторами и общая дисперсия будет равна остаточной. Если другие факторы не оказывают влияние, то остаточная дисперсия =0 и общая дисперсия будет равна факторной.

Но т.к. не все точки (наблюдения) лежат на линии регрессии, то имеет место и влияние других факторов. Пригодность уравнения регрессии зависит от того, какая часть вариации приходиться на объясненную дисперсию. Если факторная больше остаточной, то уравнение регрессии значимо и Х влияет на У.

Теснота криволинейной связи измеряется корреляционным отношением, обозначаемым через и имеющим тот же смысл, что и r .Теоретическое корреляционное отношение может быть рассчитано по формуле: =,где 2фактор–дисперсия для теоретических значений ŷ (объясненная вариация)

2общ –дисперсия для фактических значений у (необъясненная вариация).

2фактор=2общ-2остаточ Теоретическое корреляционное отношение можно представить в виде индекса корреляции R

R (индекс корреляции)==

Будут ли совпадать r и R ? Для одних линейных функций совпадают (ŷ = a + b /x, ŷ= a + b * lnx ), для других ŷ= axb , ŷ= ea + bx ) нет, но их в Statistike используется линейные коэффициенты корреляции в силу простоты вычисления.

26. Оценка значимости коэффициента регрессии и корреляции t -критерий Стьюдента, F — критерий Фишера.

В регрессионном анализе проверке статистической значимости подвергаются коэффициенты регрессии и корреляции. При этом соответственно используются t -статистика и F -статистика. Здесь можно использовать следующую процедуру.

1) Выдвигаем основную(нулевую)-гипотезу H 0 и альтернативную H 1.

2) Выбираем уровень значимости =0,05; -ошибка первого рода. Принятие статистического решения всегда сопровождается некоторой вероятностью ошибочного заключения как в одну, так и в другую сторону. В небольшой доле случаев , гипотеза Но может быть отвергнута, в то время как на самом деле она является справедливой. Это так называемая ошибка I рода, ее вероятность = . Или, наоборот, в какой-то небольшой доле случаев мы можем принять нашу гипотезу, в то время как на самом деле она ошибочна, а справедливым оказывается некоторое конкурирующее с ней предположение — альтернативная гипотеза Н1. Это ошибка II рода. При фиксированном объеме выборочных данных величина вероятности одной из этих ошибок выбирается произвольно. Обычно задается величиной вероятности ошибочного отторжения проверяемой гипотезы. Но эту вероятность называют уровнем значимости или размером критерия. Как правило, пользуются некоторыми стандартными значениями уровня значимости (=0,1;0,5;0,025;0,01;0,005;0,001). Наиболее распространенной =0,05. Она означает, что в среднем в 5 случаях из 100 мы будем ошибочно отвергать гипотезу, но при многократном использовании данного статистического критерия.

3) Выбираем закон распределения Стьюдента или Фишера.

4) Из таблиц распределения случайных величин выбираем критические точки.

5) Рассчитать фактическое значение соответствующей статистики. Сравнить его с критическим значением и выбрать одну из альтернативных гипотез.

Рассмотрим проверку статистической значимости коэффициентов регрессии.

1) Выдвигаем основную(нулевую)-гипотезу H 0 о том, что коэффициент регрессии b статистически незначим: H 0: b =0. х не оказывает влияние на у, между x и y отсутствует линейная связь, коэффициент b статистически не значим. H 1: b 0. между x и y существует линейная связь .

2) Выбираем уровень значимости =0,05.

3) Статистическая значимость коэффициента регрессии проверяется с помощью t -критерия Стьюдента.

4) Из таблиц распределения случайных величин выбираем критические точки. Критические точки, учитывая и число степеней свободы | t /2|-двойной интервал с ( n -2) степ свободы, где n число наблюдений.

5) Определяется фактическое значение критерия Стьюдента и сравнивается полученное фактическое значение с табличным.

Для этого сначала необходимо определить остаточную — сумму квадратов. (остаточную дисперсию)

2 ост =( yi – ŷ i )2 и ее среднее квадратическое отклонение ост=

Затем определяется стандартная ошибка коэффициента регрессии по формуле:

Фактическое значение t -критерия Стьюдента для коэффициента регрессии рассчитывается как t ф=b/se(b)

6) Если фактическое значение t -критерия превышает критическое(табличное), ноль-гипотеза отклоняется и с вероятностью (1-) принимается альтернативная гипотеза о статистической значимости коэффициента регрессии. Если фактическое значение t -критерия меньше табличного, то говорят, что нет оснований отклонять ноль-гипотезу.

Значение | t ф|> t кр позволяет сделать вывод об отличии от нуля (на соответствующем уровне значимости) коэффициента регрессии и, следовательно, о наличии влияния (связи) х и у.

Можно построить доверительный интервал для b . [ b – t кр* se ( b ), b + t кр* se ( b )]- 95% доверительный интервал для b . Доверительный интервал накрывает истинное значение параметра b c заданной вероятностью (в данном случае 95%).

Н0: Дф=Дост, Н1: Дф≠Дост.

Существуют таблицы F отношений при разном уровне значимости гипотезы α и различном числе степеней свободы. Табличные значения F это максимальная величина отношения которая может иметь место при случае их расхождения, при данном уровне вероятности наличия гипотезы Н0.

Фактическое значение F -отношения признается достоверным, если оно больше табличного. В этом случае гипотеза Н0 отклоняется а с вероятностью (1- α)уравнение в целом (коэффициент корреляции) считается значимым. В противном случае уравнение регрессии считается статистически не значимым.

Величина F -критерия связанна с r 2.

Фактическую дисперсию можно представить следующим образом:

А остаточную дисперсию таким образом:

Тогда F -критерий выглядит следующим образом.

Значимость r проверяется на основе величины ошибки коэффициента корреляции.

Выдвигаются гипотезы Н0: r 2=0 – коэффициент корреляции статистически не значим и альтернативная Н1: r 2≠0 – уравнение статистически значимо. Далее все рассуждения повторяются аналогично рассмотренным выше.

27. Различные аспекты множественной регрессии (мультиколлинеарность, фиктивные переменные, проблема спецификации)

Основные гипотезы лежащие в основе модели множественной регрессии:

— Модель имеет следующую спецификацию.

yt – зависимая переменная, и имеется k – регрессоров.

— xt 1….. xtk — детерминированные (определенные) величины.

— E ( ut )=0 математическое ожидание равно нулю.

E ( ut 2)=2 дисперсия равна 2, для

— E ( ut us )=0 Математическое ожидание одновременного появления ut и us равно нулю. Условие неколлерированности случайных величин.

— utN (0,2). Случайная компонента нормально распределена.

Если выполняется 5 условие, то модель нормальная линейная регрессионная модель и оценки параметров будут иметь нормальное распределение.

Основная цель множественной регрессии–построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупность их воздействие на моделируемый показатель.

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Суть проблемы спецификации включает в себя 2 круга вопросов: отбор факторов и выбор вида уравнения регрессии.

Включение в уравнение множественной регрессии того или иного набора факторов связано, прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.

1. Они должны быть количественно измеримы. Если нужно включить в модель качественны фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.

2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.

Включение в модель факторов с высокой интеркорреляцией, может привести к нежелательным последствиям — неустойчивость и ненадежность оценок коэффициентов регрессии.

Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.

Коэффициенты интеркорреляции (т. е. корреляции между объясняющими переменными) позволяют исключить из модели дублирующие факторы. Двепеременные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если rx 1 xj 0,7.

Т.к. одним из условий построения уравнения множественной регрессии является независимость действия факторов, т.е. rx 1 xj =0, коллинеарность факторов нарушает это, условие. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии.

Предпочтение при этом отдается тому фактору, который при данной тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании — специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.

Для о ценки мультиколлинеарности ф акторов может использова ться о пределитель м атрицы п арных к оэффициентов корреляции м ежду ф акторами.

Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором р факторов, то для нее рассчитывается показатель детерминации R 2, кот фиксирует долю объяснённой вариации результативного признака за счет рассматриваемых в регрессии р факторов. Влияние других неучтенных в модели факторов оценивается как 1– R 2 с соответствующей остаточной дисперсией.

При дополнительном включении в регрессию р + 1 фактора коэффициент детерминации должен возрастать а остаточная дисперсия уменьшаться: Если же этого не происходит и данные показатели практически мало отличаются друг от друга, то включаемый в анализ фактор хр+1 не улучшает модель и является лишним фактором.

Поэтому отбор факторов обычно осуществляется в 2 стадии: на 1ой подбираются факторы, исходя из сущности проблемы; на 2ой на основе матрицы показателей корреляции определяют t -статистики для параметров регрессии.

Как правило, независимые переменные в регрессивных моделях имеют «непрерывные» области изменения (НД, уровень безработицы, з/плата и т.п.). Но м.б. переменные, которые принимают всего 2 значения, в более общей ситуации — дискретное множество значений. Необходимость в таких переменных возникает в тех случаях, когда требуется принимать во внимание качественный признак. Можно оценить соответствующие уравнения внутри каждой категории, а затем изучить различия между ними, но введение дискретных переменных позволяет оценивать одно уравнение сразу по всем категориям.

Таким образом, интерпретация оценок при фиктивных переменных зависит от способа включения этих переменных в уравнении регрессии и от самого качественного признака, который они отражают.

Рассмотрим использование фиктивных переменных на примере формирования з/пл. Пусть Х1Х2. Xn „ — набор объясняющих (независимых) переменных. Т.е первоначальная модель описывается уравнением:

y = + β1 x 1 + β2×2 + βnxn+ U , где у — размер з/пл

Мы хотим включить в рассмотрение такой фактор, как наличие или отсутствие высшего образования. Введем новую бинарную переменную d 1, полагая d 1 = 1, если человек имеет высшее образование, и d 1 = 0 в противном случае. Также введем переменную d 2, полагая d 2= 1, если работник мужчина и d 2 = 1, если женщина. Т.о., мы можем исследовать проблему дискриминации в оплате труда. Рассмотрим зависимость: y = +β1 x 1 +β2 x 2 +1 d 1 +2 d 2 + U

Можно сказать, что при наличии высшего образования средняя з/пл увеличивается на величину 1, при неизменных значениях остальных параметров. Величина параметра 2 будет свидетельствовать о превышении в среднем з/пл мужчин над з/пл женщин.

К этой системе можно применить МНК и получить оценки соответствующих коэффициентов. Тестируя гипотезу 1=2=0, мы проверяем предположение о несущественном различии в з/пл междуу категориями.

Но d такая же переменная, как и V регрессор х. Ее фиктивность состоит только в том, что она количественным образом описывает качественный признак.

Если включаемый в рассмотрение качественный признак имеет не 2, а несколько значений, то можно было бы ввести дискретную переменную, принимающую такое же количество значений. Но этого не делают, т.к. трудно дать содержательную интерпретацию соответствующему коэффициенту. В этих случаях используют несколько бинарных переменных.

28.Сисмы регрессионных уравнений. Методы оценки параметров: косвенный и 2х шаговый МНК.

При моделировании сложных экономических объектов часто приходится вводить не одно, а несколько связанных между собой уравнений, т.е. описывать модель системой уравнений. Если использовать МНК для оценивания параметров уравнений системы, то полученные оценки, скорее всего, окажутся смещенными и несостоятельными.

Рассмотрим простейшую макроэкономическую кейнсианскую модель потребления, в которой нужно оценить параметры уравнения в функции потребления: Ct = + Yt + Ut (1) и тождества

где Ct — агрегированное потребление в году t . Yt — НД в году t . It — инвестиции в экономику. Ut – случайный член. и — параметры. — склонность к потреблению.

Подставим уравнение (1) в тождество (2), преобразуем и найдем Yt : Теперь сможем найти значение Y для V момента времени t :

Первые 2 слагаемых показывают, что совокупный уровень доходов зависит от постоянной составляющей объема потребления и от объема инвестиций. Если объем инвестиций возрастет на 1 , то совокупный доход увеличится на 1/(1 — ). Эта величина называется мультипликатором. Т.к. Yt включает в себя величину Ut /(1 — ), то она автоматически оказывается коррелированной со случайным членом в уравнении (1) и т.о. нарушается 4-е условие Г-М, поэтому оценки, полученные по МНК будут смещенными, а стандартные ошибки некорректными.

Кроме того нарушается причинно-следственная связь. Модель формирования дохода, трактуемая буквально, говор о том, что величина С зависит от Y в U , но это слишком упрощенное понимание. Учитывая тождество для совокупного дохода(2),также верно (или также неверно) было бы утверждать, что значение Y зависит от С.

Получился замкнутый круг, чтоб из него выбраться, нужно преобразовать уравнения и выразить как Y , так и С через их действительные детерминанты I и U .

Для Y это уже сделано в уравнении (3). Для того чтоб получить аналогичное уравнение для С, подставим значение Y из (3) в (1) и после преобразования получим:

КМНК состоит в следующем: 1) Составляется приведенная форма модели и определяются численные значения параметров для каждого уравнения обычным МНК.

2) Путем алгебраических преобразований переходят от приведенной формы к структурной, получая тем самым численные оценки структурных параметров.

Пример: Ct = + Yt + Ut ; Yt = Ct + It — структурная форма

Ct = + + уже находится в приведенной форме

= ‘; = ‘; = Ut’ Ct’ = ‘ + ‘It + Ut’

Получили обычное уравнение регрессии для которого объясняющей переменной является It (экзогенная переменная, несвязанная с величиной Ut => в этом уравнении не нарушает предпосылок Г-М (4-еусл) и можно использовать обычный МНК и получить оценки для ‘ и ‘

Ct = a’ + b’It, где а’ и b’ — оценки для ‘ и ‘ соответственно

= a ‘; = b ‘ => a = ; b = Т.к. мы можем получить единственное выражение для а и b через а’ и b ‘, то уравнение называется однозначно определенным (идентифицируемым).

1. Строится приведенная форма модели и определяются ее параметры обычным МНК.

2. Выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры кот-го определяют 2х шаговым МНК и находят их расчетные (теоретические) значения по соответствующим уравнениям приведенной формы модели.

3. Обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения для предопределенных переменных и расчетные значения для эндогенных переменных, стоящих в правой части данного структурного уравнения.

— функция заработной платы.

Ct – расходы на конечное потребление в периоде t ; Yt и Yt -1 – совокупный доход период t и t -1; It – валовые инвестиции; St – расходы на заработную плату; Gt – государственные расходы; u 1, u 2, u 3 – случайные компоненты.

Эндогенные переменные: Ct , It , St , Yt .

Предопределенные: лаговые — Yt -1

экзогенные – t , Gt

1) 3-1=3-1 – точно идентифицировано

2) 3-1 > 1-1 – сверхидентифицированно

3) 3-1 > 2-1 – сверхидентифицированно

Т.к. 1 уравнение структурной формы точно идентифицируемо, то его параметры можно оценить КМНК. Для этого обычным МНК определяются параметры каждого уравнения приведенной формы, а затем по соответствующим выражениям находятся параметры структурной формы.

2 уравнение системы модели сверхидентифицированно, но правая часть уравнения не содержит эндогенных переменных, поэтому не происходит нарушений предпосылок обычного МНК и причинно — следственных связей. Следовательно это уравнение можно оценить обычным МНК в структурной форме.

3 уравнение системы так же сверхидентифицированно, в правой части содержатся эндогенная переменная Yt . Что приводит к нарушению предпосылок МНК. Параметры этого уравнения можно определить ДМНК.

Для этого определим обычным МНК параметры 4 уравнения в приведенной форме. Подставляя в идентифицируемое приведенное уравнение все наблюдения, получаем расчетные (теоретические) значения . Обычным МНК определяются параметры 3 уравнения структурной формы используя при этом фактические значения для St и Yt -1 и расчетное значение вместо yt .

29. Системы регрессионных уравнений как эконометрическая модель . Проблема идентифицируемости.

При моделировании сложных экономических объектов часто приходится вводить не одно, а несколько связанных между собой уравнений, т.е. описывать модель системой уравнений.

Структурная и приведенная формы модели.

Уравнения, составляющие исходную модель, называются структурными уравнениями модели (структурной формой) Их можно разделить на 2 группы: поведенческие уравнения , описывающие эмпирические взаимосвязи между переменными, и уравнения — тождества . Тождества не содержат каких-либо подлежащих оценке параметров, а также не включают случайного члена.

Уравнения, показывающие как в действительности определяются значения эндогенных переменных, называются уравнениями в приведенной форме (приведенная форма модели). Это уравнения, в которых эндогенные переменные выражены исключительно через экзогенные переменные и случайные составляющие уравнений

Кроме этого уравнения могут содержать лаговые переменные. Экзогенные и лаговые переменные совместно называются предопределенными переменными. Лаговые–это те же переменные, но за предшествующие промежутки времени.

Эндогенные и экзогенные переменные. Проблема идентифицируемсти.

В процессе оцениваются различные эндогенные и экзогенные переменные. Эндогенные — это те переменные, значения которых определяются внутри модели (всегда стоят в левой части), экзогенными являются переменные, значения, которых определяются вне модели и, следовательно, берутся как заданные. Модель не объясняет как получаются значения этой переменной, они просто используются как наперед заданные.

Возможность применения КМНК и ДМНК связанны с проблемой идентификации, т.е. с однозначным определением параметров.

Если структурные параметры однозначно определяются по приведенным коэффициентам, то говорят что данное уравнение точно идентифицировано. Если из приведенной формы модели можно получить несколько оценок структурных параметров, то говорят, что уравнение сверхидентифицированно. Если структурны параметры модели нельзя получить через приведенные коэффициенты, то такое уравнение называется неидентифицированным.

Существует порядковое условие идентификации (Четное правило).

Это условие применяется для проверки возможности идентификации структурной формы модели. Для этого по каждому уравнению и для модели в целом подсчитывают: К – число предопределенных переменных модели; k — число предопределенных переменных в каждом уравнении; m -число эндогенных переменных в каждом уравнении.

Для каждого уравнения проверяют соотношение:

1) Если это выражение выполняется как строгое неравенство (>), то данное уравнение сверхидентифицированно. 2) (=) – точноидентифицированно.

На идентификацию не надо проверять тождества, т.к. они не содержат параметров, подлежащих оценке, но переменные, входящие в тождества, учитываются при подсчете общего числа эндогенных и предопределенных переменных модели.

R — значит регрессия

Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума.

Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей.

Введение в регрессионный анализ

Если имеется корреляционная зависимость между переменными y и x , возникает необходимость определить функциональную связь между двумя величинами. Зависимость среднего значения называется регрессией y по x .

Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей минимальна.

Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.

Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений вокруг регрессии является дисперсия.

• k — число коэффициентов в системе уравнений регрессии.

Чаще всего используется модель линейной регрессии, а все нелинейные зависимости приводят к линейному виду с помощью алгебраических ухищрений, различных преобразования переменных y и x .

Линейная регрессия

Уравнения линейной регрессии можно записать в виде

В матричном виде это выгладит

• y — зависимая переменная;
• x — независимая переменная;
• β — коэффициенты, которые необходимо найти с помощью МНК;
• ε — погрешность, необъяснимая ошибка и отклонение от линейной зависимости;

Случайная величина может быть интерпретирована как сумма из двух слагаемых:

• — полная дисперсия (TSS).
• — объясненная часть дисперсии (ESS).
• — остаточная часть дисперсии (RSS).

Еще одно ключевое понятие — коэффициент корреляции R 2 .

Ограничения линейной регрессии

Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных.

1. Линейность, собственно. Увеличение, или уменьшение вектора независимых переменных в k раз, приводит к изменению зависимой переменной также в k раз.
2. Матрица коэффициентов обладает полным рангом, то есть векторы независимых переменных линейно независимы.
3. Экзогенность независимых переменных — . Это требование означает, что математическое ожидание погрешности никоим образом нельзя объяснить с помощью независимых переменных.
4. Однородность дисперсии и отсутствие автокорреляции. Каждая ε_i обладает одинаковой и конечной дисперсией σ 2 и не коррелирует с другой ε_i. Это ощутимо ограничивает применимость модели линейной регрессии, необходимо удостовериться в том, что условия соблюдены, иначе обнаруженная взаимосвязь переменных будет неверно интерпретирована.

Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике.

Неоднородность дисперсии

При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки.

Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно.

Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены.

• Автокорреляция проверяется статистикой Дарбина-Уотсона (0 ≤ d ≤ 4). Если автокорреляции нет, то значения критерия d≈2, при позитивной автокорреляции d≈0, при отрицательной — d≈4.
• Неоднородность дисперсии — Тест Уайта, , при \chi<^2>_<\alpha;m-1>$» data-tex=»inline»/> нулевая гипотеза отвергается и констатируется наличие неоднородной дисперсии. Используя ту же можно еще применить тест Бройша-Пагана.
• Мультиколлинеарность — нарушения условия об отсутствии взаимной линейной зависимости между независимыми переменными. Для проверки часто используют VIF-ы (Variance Inflation Factor).

В этой формуле — коэффициент взаимной детерминации между и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности.

Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений.

Как преодолеть эти ограничения

Нарушения одной или нескольких ограничений еще не приговор.

1. Нелинейность регрессии может быть преодолена преобразованием переменных, например через функцию натурального логарифма ln .
2. Таким же способом возможно решить проблему неоднородной дисперсии, с помощью ln , или sqrt преобразований зависимой переменной, либо же используя взвешенный МНК.
3. Для устранения проблемы мультиколлинеарности применяется метод исключения переменных. Суть его в том, что высоко коррелированные объясняющие переменные устраняются из регрессии, и она заново оценивается. Критерием отбора переменных, подлежащих исключению, является коэффициент корреляции. Есть еще один способ решения данной проблемы, который заключается в замене переменных, которым присуща мультиколлинеарность, их линейной комбинацией. Этим весь список не исчерпывается, есть еще пошаговая регрессия и другие методы.

К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель.

Линейная регрессия плюсов на Хабре

Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.

Загружает данные из tsv файла.

• points — Рейтинг статьи
• reads — Число просмотров.
• comm — Число комментариев.
• faves — Добавлено в закладки.
• fb — Поделились в социальных сетях (fb + vk).
• bytes — Длина в байтах.

Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных.

Теперь собственно сама модель, используем функцию lm .

В первой строке мы задаем параметры линейной регрессии. Строка points

. определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points

reads , набор переменных — points

Перейдем теперь к расшифровке полученных результатов.

• Intercept — Если у нас модель представлена в виде , то тогда — точка пересечения прямой с осью координат, или intercept .
• R-squared — Коэффициент детерминации указывает насколько тесной является связь между факторами регрессии и зависимой переменной, это соотношение объясненных сумм квадратов возмущений, к необъясненным. Чем ближе к 1, тем ярче выражена зависимость.
• Adjusted R-squared — Проблема с в том, что он по любому растет с числом факторов, поэтому высокое значение данного коэффициента может быть обманчивым, когда в модели присутствует множество факторов. Для того, чтобы изъять из коэффициента корреляции данное свойство был придуман скорректированный коэффициент детерминации .
• F-statistic — Используется для оценки значимости модели регрессии в целом, является соотношением объяснимой дисперсии, к необъяснимой. Если модель линейной регрессии построена удачно, то она объясняет значительную часть дисперсии, оставляя в знаменателе малую часть. Чем больше значение параметра — тем лучше.
• t value — Критерий, основанный на t распределении Стьюдента . Значение параметра в линейной регрессии указывает на значимость фактора, принято считать, что при t > 2 фактор является значимым для модели.
• p value — Это вероятность истинности нуль гипотезы, которая гласит, что независимые переменные не объясняют динамику зависимой переменной. Если значение p value ниже порогового уровня (.05 или .01 для самых взыскательных), то нуль гипотеза ложная. Чем ниже — тем лучше.

Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями.

Проверим значения параметров линейной регрессии.

Как видим в целом отзывчивость модели возросла, параметры подтянулись и стали более шелковистыми , F-статистика выросла, так же как и скорректированный коэффициент детерминации .

Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.

И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.

В заключение

Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки.

Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так.