Разностные уравнения рекурсивных и нерекурсивных фильтров
Читайте также:
|
Важную роль в системах обработки сигналов играют рекурсивные фильтры 1-го и 2-го порядков.
• Базовый рекурсивный фильтр 1-го порядка. Базовым РФ 1-го порядка называют фильтр, описываемый разностным уравнением вида:
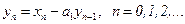
Применив z-преобразование к левой и правой частям уравнения, получим
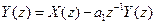
Следовательно, передаточная функция фильтра имеет вид

• Рекурсивный фильтр 1-го порядка. Разностное уравнение имеет вид:
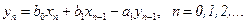
Применив z-преобразование к левой и правой частям уравнения, получим
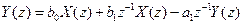

• Базовый рекурсивный фильтр 2-го порядка.Разностное уравнение и передаточная функция имеют вид:
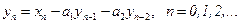
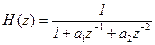
• Рекурсивный фильтр 2-го порядка. Разностное уравнение и передаточная Функция имеют вид:

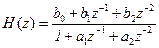
• Нерекурсивный фильтр 2-го порядка. Разностное уравнение и передаточная функция имеют вид:
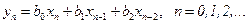
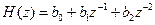
На основе приведенных примеров можно сформулировать мнемоническое правило определения передаточной функции по разностному уравнению (и наоборот):
• коэффициенты разностного уравнения являются коэффициентами передаточной функции;
• коэффициенты разностного уравнения 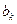

• коэффициенты разностного уравнения bk при xn—k равны коэффициентам знаменателя передаточной функции (с обратным знаком) при z — k , k = О, 1. N
Пример. Известна передаточная функция рекурсивного фильтра
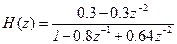
Разностное уравнение имеет вид:

• В общем случае передаточная функция дискретного фильтра может быть получена путем применения z-преобразования к разностным уравнениям (1) и (2). Рекурсивный фильтр:
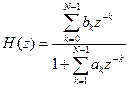
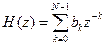
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)
Рекурсивный цифровой фильтр разностное уравнение


21.6. ЦИФРОВЫЕ ФИЛЬТРЫ, ИХ РАЗНОСТНЫЕ УРАВНЕНИЯ, ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ИМПУЛЬСНЫЕ ХАРАКТЕРИСТИКИ
Цифровой фильтр описывается тремя характеристиками разностным уравнением , которому может быть поставлена в соответствие передаточная функция K ( z ) или полученная в результате обратного z -преобразования K ( z ) его дискретная импульсная характеристика h [ k ] . Из приведенных примеров следует, что существуют два принципиально различных класса цифровых фильтров. Фильтры первого класса нерекурсивные описываются разностным уравнением, в котором выходная величина y [ k ] выражается только через конечное число значений входного сигнала x [ n ] . Таким, например, является уравнение усреднения, рассмотренное выше.
Фильтры второго класса рекурсивные описываются уравнением, в котором выходная переменная y [ k ] выражается не только через значения входного сигнала x [ n ], но и через предшествующие значения выходного сигнала y [ k – m ] . Сюда, например, относится разностное уравнение u2[ k + 1] = u2[ k ] e -T/ t + u1[ k ][h(T) – h(T – Tи)], описывающее преобразование прямоугольных сигналов RС -цепью (см. п. 20.4), а также дискретные модели любых других аналоговых динамических систем (в частности, электрических цепей).
Нерекурсивный цифровой фильтр сохраняет информацию о входном сигнале за конечное число шагов его импульсная характеристика конечна, а передаточная функция имеет вид ряда по степеням z (который включает и отрицательные показатели).
Информация, поступившая на вход рекурсивного фильтра, сохраняется в нем бесконечно долго; он имеет бесконечную по длительности импульсную характеристику и описывается передаточной функцией в виде рациональной дроби. Максимальная разность индексов переменных в разностном уравнении, который отвечает разность степеней z в числителе и знаменателе передаточной функции, определяет порядок цифрового фильтра.
Так, нерекурсивный цифровой фильтр второго порядка описывается разностным уравнением f 2 [ n ] = a 0 f 1 [ n ] + a 1 f 1 [ n – 1] + a 2 f 1 [ n – 2], его передаточная функция K ( z ) = a 0 + a 1 z –1 + a 2 z –2 , а импульсная характеристика определяется коэффициентами, h [ n ] = a 0 , a 1 , a 2 , 0, 0, 0, 0, .
Рекурсивный цифровой фильтр второго порядка описывается разностным уравнением f 2 [ n ] = a 0 f 1 [ n ] + a 1 f 1 [ n – 1] + a 2 f 1 [ n – 2] + b 1 f 2 [ n – 1] + b 2 f 2 [ n – 2],
а его передаточная функция 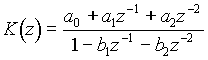
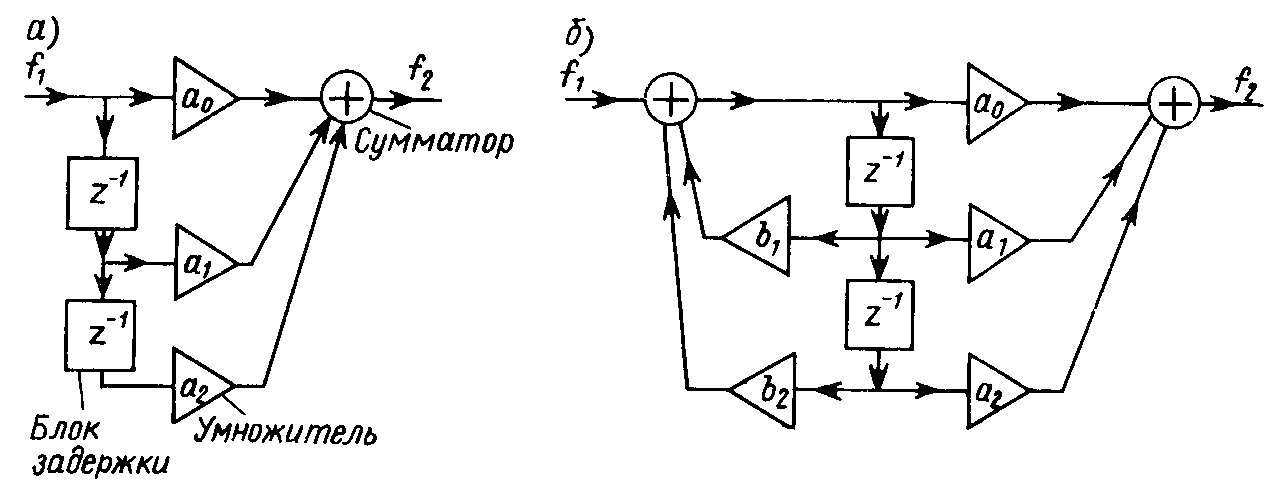
По известным значениям коэффициентов разностного уравнения a k и b k цифровой фильтр 2-го порядка может быть реализован с помощью умножителей, сумматоров и блоков задержки.
Блок-схемы цифровых фильтров обоих классов 2-го порядка, включающие перечисленные блоки, показаны на рис. 21.10 ( а – нерекурсивный; б – рекурсивный).
Цифровые рекурсивные фильтры. Часть 1.
Я долго думал, как назвать тему. Вариантов было много: от рекламно-жизнерадостного «Цифровые фильтры — это очень просто!» до (с ярким оттенком снобизма) «Алгоритмы построения цифровых IIR- фильтров Баттерворта — для тупых!»
«По совету друзей» (с) я решил остановиться на нейтральном названии (простенько, но со вкусом (с)): «Цифровые рекурсивные фильтры», или, как их ещё называют в простонародье, «БИХ-фильтры» или фильтры с Бесконечной Импульсной Характеристикой, что эквивалентно буржуйскому IIR (infinite impulse response).
Моя цель — подготовить подготовить вас к чтению серьёзных статей по этой тематике (не дай Бог, конечно, но в жизни может всякое случиться. ).
Продолжение в Часть 2. Часть 3.
Что от вас требуется:
1. Умение пользоваться Googleм (многие термины я объяснить подробно не смогу)
2. Знание математики в пределах 1 курса технического ВУЗа или продвинутое (см. пункт 1)
3. Знание программирования. Язык значения не имеет. Я буду приводить примеры на том языке, который под руку попадёт. В основном это будет Си и Фортран.
Претензии любителей Бэйсика, Дельфи, МатЛаба и PHP не принимаются.
I. Комплексная передаточная характеристика аналогового фильтра низких частот (ФНЧ).
«Аналоговый фильтр — это такая хрень устройство из сопротивлений, индуктивностей и конденсаторов» (с).Если кто ещё помнит ТОЭ (теоретические основы электротехники), комплексное сопротивление индуктивности
Z=jωL, конденсатора: Z=1/(jωC) где j — мнимая единица, ω- круговая частота
H(jω) — комплексная передаточная характеристика фильтра. То что в скобках стоит jω просто подчёркивает «комплексность» этой функции.H(jω) полностью описывает АЧХ (амплитудно-частотную характеристику) и ФЧХ (фазо-частотную характеристику) фильтра.Обычно обозначают jω=S.
Аналоговые фильтры давно и хорошо изучены. Здесь всё уже украдено придумано до нас.
Вот например:
Аналоговый ФНЧ Баттерворта 1 порядка: 
Аналоговый ФНЧ Баттерворта 2 порядка: 
Аналоговый ФНЧ Баттерворта 3 порядка: 
Параметр β определяет частоту среза фильтра.
II. z- преобразование.
Наша задача превратить аналоговый ФНЧ в цифровой фильтр.
Чтобы перейти к цифровому фильтру надо сделать z-преобразование H(S)—> H(z)
Для ФНЧ z-преобразование имеет вид: 
Для ФВЧ z-преобразование имеет вид: 
Для фильтров низких порядков это легко: тупо подставляем в формулу Н(S) формулу S(z).
Давайте найдём H(z) ФВЧ 2-го порядка: 
Упрощаем: 
Окончательно: 
В принципе, цифровой ФВЧ Баттерворта 2 порядка готов! Можно писать рекуррентную формулу 🙂
В общем виде H(z) 2-го порядка: 
Тогда: 


Fs -частота среза фильтра, FN — частота Найквиста
α — параметр, определяющий по какому уровню мы определяем Fs.
Можно положить α=1, что соответствует уровню -3дБ.
Итак, мы определили коэффициенты H(z) для ФВЧ.
Соответствующая рекуррентная формула: 
Примечание: Обычно, чтобы не тащить в рекуррентную формулу сомножитель 1/Ao, в формуле H(z) числитель и знаменатель умножают на 1/Ao.
Если мы проведём такие же выкладки для ФНЧ, то получим, что нечётные коэффициенты поменяют знаки.
A1фнч=-A1фвч и B1фнч=-B1фвч.
III. Матрица z- преобразования.
Пока порядок фильтра не очень высок, коэффициенты фильтра определить легко. На высоких порядках получаются многоэтажные дроби, которые трудно упростить.
Поэтому воспользуемся матрицами z -преобразования.
Для ФНЧ Баттерворта 2-го порядка: 
Соответствующая матрица z- преобразования ФНЧ-ФВЧ имеет вид:

То есть умножая матрицу z- преобразования на столбец, состоящий из коэффициентов H(S), сразу получаем искомые коэффициенты рекуррентной формулы!
Заметим, чтобы получить матрицу z- преобразования ФВЧ надо у матрицы z- преобразования ФНЧ переставить столбцы (и наоборот).
Матрицу z- преобразования относительно просто вычислить.
Вот пример матрицы ФНЧ 15 порядка:
Матрица z-преобразования зависит только от порядка фильтра. Сам фильтр может быть любым — Баттерворта, Чебышева 1 и 2 рода, Кауэра. Естественно и коэффициенты Bn придётся вычислять при помощи этой матрицы.
Сложнее дело обстоит с полосовыми и режекторными фильтрами. Матрица z-преобразования также существует, но имеет более сложный вид.
Пусть аналоговый ФНЧ- прототип 6-го порядка имеет вид: 
Матрица ПФ 6 порядка: 
К- параметр определяющий центральную частоту фильтра.
Искомые коэффициенты рекуррентной формулы Ai, Bi определяются из уравнений, где ai, bi — коэффициенты H(S): 

Для практической реализации осталось только определить параметр К.
z- преобразование ФНЧ—> ПФ имеет вид: 
где 
F0 — центральная частота, FN- частота Найквиста, Fs- частота среза ФНЧ — прототипа (полоса фильтра).
IV. Быстрый алгоритм вычисления коэффициентов рекуррентной формулы.
В реальных вычислениях матрица принимает более простой вид из-за симметрии коэффициентов по столбцам. (Количество умножений уменьшается почти в 2 раза).
Рассмотрим алгоритм быстрого расчёта коэффициентов рекуррентной формулы на примере полосового фильтра 6 порядка.Переставим строки (для наглядности).
Вот так рассчитываются коэффициенты по «обычному» алгоритму: 
Обнулим элементы матрицы, выделенные желтым цветом: 
Получили разряженную матрицу, но «потеряли» значения искомых коэффициентов Аi.
А теперь элементарно восстановим «потерянные» значения Аi: 
Аналогично находятся коэффициенты Вi.
V. Практическая реализация.
Программа расчёта коэффициентов полосового фильтра 5 порядка быстрым методом:
Рекуррентная формула для полосового БИХ-фильтра 5-го порядка будет иметь вид:
y[n]=B[0]*x[n]+B[1]*x[n-1]+B[2]*x[n-2]+B[3]*x[n-3]+B[4]*x[n-4]+B[5]*x[n-5]+B[6]*x[n-6]+
B[7]*x[n-7]+B[8]*x[n-8]+B[9]*x[n-9]+B[10]*x[n-10]-
-A[1]*y[n-1]-A[2]*y[n-2]-A[3]*y[n-3]-A[4]*y[n-4]-A[5]*y[n-5]-A[6]*y[n-6]-
-A[7]*y[n-7]-A[8]*y[n-8]-A[9]*y[n-9]-A[10]*y[n-10]
где x[n] — входные выборки, y[n] — выходной (отфильтрованный) сигнал.
Эффективность алгоритма.
Процессор Intel Atom 1.6 ГГц
Фильтр — полосовой фильтр Кауэра 5 порядка.
Рассчитывалось 5 млн. фильтров с одинаковой полосой, менялась только центральная частота.
Время расчёта коэффициентов по обычной методике — 46 секунд.
Время расчёта быстрым методом — 28 секунд.
Можно сравнить с медленным алгоритмом:
http://forum.easyelectronics.ru/viewtopic.php?f=9&t=22252&start=0
Более простая программа:
Вычисление коэффициентов полосового фильтра Баттерворта 3 порядка на ATmega8:
Рекуррентная формула для полосового БИХ-фильтра 3-го порядка будет иметь вид:
y[n]=B[0]*x[n]+B[1]*x[n-1]+B[2]*x[n-2]+B[3]*x[n-3]+B[4]*x[n-4]+B[5]*x[n-5]+B[6]*x[n-6]-
-A[1]*y[n-1]-A[2]*y[n-2]-A[3]*y[n-3]-A[4]*y[n-4]-A[5]*y[n-5]-A[6]*y[n-6]
где x[n] — входные выборки, то y[n] — выходной (отфильтрованный) сигнал.
VI. Приложение.
Матрицы z — преобразования ФНЧ-ФНЧ порядков 1-4: 
Свойства матрицы z — преобразования:
Сумма элементов столбцов (кроме крайнего левого (ФВЧ) или правого(ФНЧ)) равна 0.
Сумма элементов нечётных строк = 0.
Матрицы z — преобразования ФНЧ—> ПФ порядков 2-3:
http://eelib.narod.ru/toe/Novg_2.01/21/Ct21-6.htm
http://we.easyelectronics.ru/Theory/cifrovye-rekursivnye-filtry-chast-1.html