Реологические свойства дисперсных систем
Основные понятия
Реология – наука о деформации и течении материалов
К реологическим свойствам относятся вязкость и текучесть.
Вязкость (η) — внутреннее трение между слоями данного вещества (жидкости или газа) движущимися относительно друг друга.
Оно обусловлено взаимодействием между молекулами. У газов внутреннее терние имеет кинетическую природу, поэтому при увеличении Т сила терния возрастает.
У жидкостей и тв. тел — внутреннее трение имеет энергетическую природу, поэтому при увеличении температуры сила терния убывает.
Текучесть – свойство, противоположное вязкости – τ =1/ η.
При увеличении числа частиц и сил взаимодействия между ними в дисперсных системах образуется структура.
Структура – пространственный каркас, состоящий из частиц дисперсной фазы и заполненный дисперсионной средой.
В связнодисперсных системах частицы дисперсной фазы не способны перемещаться относительно друг друга. Они обладают определенными механическими свойствами: упругостью, вязкостью, пластичностью. Совокупность механических свойств, обусловленных структурой, называются структурно-механическими.
Структуры согласно Петру Александровичу Ребиндеру (*) в коллоидных системах можно разделить по видам взаимодействия частиц дисперсной фазы на:
1. Коагуляционные, в которых взаимодействие частиц происходит непосредственно через прослойку жидкости за счет сил межмолекулярного взаимодействия. Механические свойства определяются не столько свойствами частиц, образующих структуру, сколько характером и особенностями связи и прослоек среды.
Коагуляционные структуры имеют жидкую дисперсионную среду. Для этих структур характерно явление тиксотропии – способность структурированной системы восстанавливаться после разрушения.
2. Конденсационно-кристаллизационные– образуются за счет непосредственного химического взаимодействия между частицами и их срастания с образованием жесткой объемной структуры.
Если частицы дисперсной фазы аморфные, то образуются конденсационныеструктуры,
Если частицы кристаллические – то кристаллизационные. Такие структуры характерны для связнодисперсной структуры с твердой дисперсионной средой. Такие структуры придают телам прочность, хрупкость и не восстанавливаются после разрушения.
Структурированные системы способны к деформациям.
Деформация – относительное смещение точек системы, при которых не нарушается ее сплошность.
Деформации бывают упругие (обратимые) и остаточные.
При упругой деформации структура тела полностью восстанавливается после снятия нагрузки.
Остаточная деформация необратима.
Остаточная деформация, при которой не происходит разрушение, называется пластической.
Среди упругих деформаций различают объемные: растяжение, сжатие тела, они вызываются нормальным напряжением сдвига. При одномерном удлинении отношение приращения длины к первоначальной величине называется γ=Δl/l0 – абсолютным удлинением.
деформация сдвига – деформация кручения, возникает под действием касательного, тангенциального напряжения сдвига, определяется относительным сдвигом под действием напряжения сдвига.
Жидкость и газы деформируются при минимальных нагрузках, под действием разности давлений текут. Но жидкости при течении практически не сжимаются, их плотности практически постоянны.
Такие свойства, как упругость, пластичность, вязкость и прочность проявляются при сдвиговой деформации, которая считается наиболее важной в реальных исследованиях.
Зависимость реологических свойств от различных факторов выражают графически в виде реологических кривых (кривых течения).
Для жидкости характерны два течения:
а) ламинарное в виде параллельных неперемешивающихся слоев
Реологические модели
В реологии механические свойства материалов представляют в виде реологических моделей, в основе которых лежат три закона, связывающих напряжение сдвига и деформацию. Им соответствуют 3 идеальных модели идеализированных материалов, отвечающих таким свойствам, как упругость, пластичность, вязкость:
1. Идеальное упругое тело Гука ( *)
Его можно представить в виде пружины
Е-модуль упругости Юнга, характеризует
L упругие свойства тела: Екрист.=10 9 Па, Емет=10 11 Па.
Рис.4.2. Модель упругого тела Гука
Е=ctg 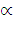
Реологическая кривая представлена на рис. 4.3:
Рис.4.3. Реологическая кривая упругого тела Гука
2. Идеальное вязкое тело Ньютона ( *) представляет собой поршень с отверстиями, помещенный в цилиндр с жидкостью
Рис. 4.4.Модель идеально вязкого тела Ньютона
Идеально вязкая жидкость течет в соответствии с законом Ньютона:
Ньютоновскими жидкостями называют системы, течение которых подчиняется закону Ньютона:
Напряжение сдвига при ламинарном течении жидкости с вязкостью η пропорциональна градиенту ее скорости.

Здесь P — напряжение сдвига, вызывающее течение жидкости; dU/dx — градиент скорости, т.е. различие в скоростях ламинарного течения двух слоев жидкости, отстоящих друг от друга на расстоянии х, отнесенное к этому расстоянию; h — коэффициент вязкости, который для краткости называют вязкостью (динамической вязкостью). Величину h/r называют кинематической вязкостью, где r — плотность жидкости.
Вязкость характеризует способность тел оказывать сопротивление внешнему напряжению, вызывающему течение.
Физический смысл коэффициента вязкости – вязкость равна силе трения между слоями жидкости при площади соприкасающихся слоев жидкости равной 1 м 2 и градиенте скорости, равном 1.
Чем больше вязкость тела, тем «неохотнее», т.е. с меньшей скоростью оно течет под действием одного и того же напряжения.
В системе СИ значения h выражают в Па×с. Для газов вязкость изменяется в пределах: 1 — 100 мкПа×с, для воды при 20 0 С h = 1мПа×с. Часто используют и внесистемную единицу измерения вязкости — пуаз [П] = [г/(см×с)], вязкость воды при 20 0 С равна 0,01П или одному сантипуазу (сП), равному 10 Па с.
Рассмотрим понятие градиента скорости. Представим жидкость, ламинарно текущую под действием силы тяжести при плоскопараллельном течении через цилиндрический капилляр со скоростью U. Однако не вся жидкость течет с одной скоростью, скорость потока максимальна в центре капилляра, а к стенкам капилляра потоки жидкости текут с меньшей скоростью из-за адгезии к стенкам сосуда.
Скорость движения слоя, непосредственно прилегающего к стенке (слой Прандтля), за счет сил адгезии равна нулю, тогда как центральный слой жидкости движется с максимальной скоростью. 


Рис.4.5. Эпюра скоростей текущей в капилляре жидкости
Если для каждого слоя изобразить направление и скорость течения вектором и соединить концы, получим эпюру скоростей в капилляре.
Если скорость движения обозначить dy/dt , а y и t — независимые переменные, изменим порядок дифференцирования:
dU /dx = d 2 y/ (dt dx)= dγ /dt = 


Согласно уравнению течения, для ньютоновских жидкостей наблюдается линейная зависимость dU/dx от Р. Таким образом, вязкость ньютоновских жидкостей не зависит от напряжения сдвига, она равна котангенсу угла наклона прямых в указанных координатах (графический смысл коэффициента вязкости). При ламинарном течении на вязкость η ньютоновских жидкостей влияет лишь температура.
Зависимость реологических свойств от различных факторов выражают в виде реологических кривых (кривых течения): h = f(p) или dU/dx = f(p).
Согласно (4.2) для ньютоновских жидкостей наблюдается линейная зависимость dU/dx (рис.4.6).
Рис.4.6. Реологические кривые для ньютоновских жидкостей
Это означает, что вязкость ньютоновских жидкостей не зависит от напряжения сдвига, и равна котангенсу угла наклона (a) прямой на рис.4.6; при ламинарном их течении h зависит лишь от температуры и природы жидкости.
В свою очередь деформация γ ньютоновских жидкостей линейно зависит от времени развития при постоянной нагрузке : γ=(Р/ η) t
Рис.4.7. Кинетика развития деформации для ньютоновских жидкостей
Измерить величину динамической вязкости можно различными способами, например, по скорости вытекания жидкости из капилляров.
Пуазейль (54) получил эмпирическое уравнение, согласно которому объем жидкости, вытекающий из капилляра, зависит как от параметров капилляра – длины l и диаметра r, так и давления P, под которым она продавливается через капилляр, вязкости жидкости η и времени вытекания t:

Обозначим постоянные для данного вискозиметра параметры через k. Для ньютоновской жидкости при постоянном объеме вязкость
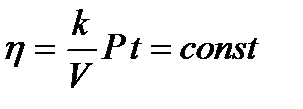
и определяется только по времени вытекания из капилляра.
3. Модель идеально-пластического тела Сен-Венана-Кулона (**)
Р Модель представляет собой твердое тело на плоскости, при движении которого возникает постоянное трение, не зависящее от нормального напряжения сдвига – закон «сухого трения»: деформация отсутствует, если Р 0, g¢>0, течение идет с любой скоростью
Рис. 4.9. Реологическая кривая модели Сен-Венана-Кулона
К элементу «сухого трения» нельзя приложить напряжение Р>Рт, тело разрушается, сопротивление отсутствует.
4. Модель реального тела. Модель Бингама ( * ) – вязкопластическое тело
При последовательном соединении элементов
При параллельном соединении элементов
Рис. 4.10. Модель Бингама: параллельное соединение жидкостного элемента(поршень в цилиндре) и тела Сен-Венана
Рис.4.11. Реологические кривые модели Бингама
Закон Бингама: Р = Рт +h¢ g¢, (4.7)
причем Р включает две составляющие: разрушающее структуру и вызывающее течение.
По физическому смыслу h и h¢ отличаются, т.к.
h= h¢ + Рт /g¢ = 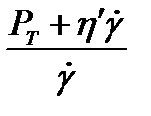
ньютоновская вязкость учитывает все сопротивления течению, а пластическая не учитывает прочность структуры, но отражает скорость разрушения, в основном вязкостью дисперсионной среды, которая может меняться в широких пределах. Например, для газов вязкость равна примерно 10 -5 Па с , для стекол и твердых тел – 10 15 — 10 20 Па с и более.
Течение такой системы начинается лишь тогда, когда напряжение сдвига превысит какое-то определенное критическое значение PТ, необходимое для разрушения структуры. Такое течение Бингам назвал пластическим, а напряжение сдвига PТ — пределом текучести. С точки зрения реологии такие системы называют пластично — вязкими, и закономерности их течения описываются уравнением Бингама.
При отсутствии структурной сетки значение PТ = 0 и уравнение Бингама переходит в уравнение Ньютона, а пластическая вязкость — в истинную вязкость ньютоновской жидкости. Графическое изображение уравнения Бингама представлено на рис.4.11.
Рис.4.12. Кривая течения бингамовской (а) и реальной пластично-вязкой системы (б).
Согласно рис.4.12, при нагрузках, превышающих Рт, происходит скачкообразное разрушение структуры, и пластическая вязкость принимает постоянное значение:

Примером систем, хорошо подчиняющихся уравнению Бингама, могут служить пасты из глины и консистентные смазки. Однако для большинства структурированных систем зависимость dU/dx от P выражается не прямой, а кривой (рис.4.12.б). Причина этого явления заключается в том, что при достижении предела текучести структура разрушается не сразу, а постепенно по мере увеличения Р и dU/dx.
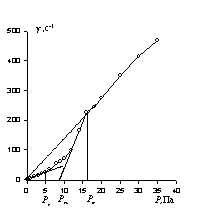
На кривой можно выделить три критических напряжения сдвига:
1) Pn — минимальный предел текучести, соответствующий началу течения; 2) Pт — предел текучeсти по Бингаму, отвечающий отрезку на оси абсцисс, отсекаемому продолжением прямолинейного участка кривой;
3) Pm — максимальное напряжение сдвига, соответствующее значению P, при котором кривая переходит в прямую линию.
В области кривой (Pn — Pm) вязкость не является постоянной величиной и по мере увеличения P уменьшается. При P > Pm структура жидкости разрушается полностью и вязкость принимает постоянное наименьшее для данной системы значение.
4.4. Реологические кривые жидко- и твердообразных структурированных дисперсных систем
При рассмотрении результатов исследования реологических свойств структурированных систем можно выделить два характерных типа полных реологических кривых для систем
— с жидкообразной структурой, у которых течение начинается вслед за приложением напряжения (рис. 2.40);
– с твердообразной структурой, течение которых начинается только после некоторого предельного напряжения (рис. 2.41).
Полные реологические кривые характерны для течения относительно разбавленных растворов полимеров, поверхностных слоев ПАВ, некоторых тиксотропных дисперсий. В таких системах образуются жидкообразные структуры. При постоянном напряжении сдвига, время действия которого больше периода релаксации, устанавливается стационарное течение. При небольшом напряжении сдвига система течет без разрушения структуры с высокой вязкостью h0 (участок 0 – Рs на рис. 2.40). Отмеченное на оси значение Рs, называемое статическим напряжением сдвига, является критическим напряжением, которое необходимо для разрушения структуры, образовавшейся в системе в статических условиях. При этом первом критическом напряжении сдвига начинается частичное обратимое разрушение структуры.
Рис. 2.40. Полные реологические кривые течения жидкообразной структурированной системы
Рис. 2.41. Полные реологические кривые твердообразной структурированной системы
При напряжении Рsk разрушение структуры завершается. Следовательно, Рsk – то критическое напряжение сдвига, которое необходимо для полного разрушения структуры, образовавшейся в стационарных условиях. Если бы в системе не восстанавливалась обратимо тиксотропная структура, то при Р >Рsk система обладала бы свойствами истинной ньютоновской жидкости.
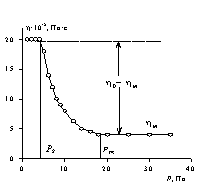
Однако для течения жидкой структурированной системы часть работы будет расходоваться на разрушение этой тиксотропно восстанавливающейся структуры, а Рm – напряжение, после которого жидкость приобретает свойства ньютоновской жидкости, т.е. то критическое максимальное напряжение, необходимое для полного разрушения структуры, образовавшейся в статических условиях и восстанавливающейся в динамических. Все критические значения напряжения сдвига можно выявить только на полной реологической кривой в координатах «g– Р». При выражении полной реологической кривой в координатах «hef– Р» можно достаточно четко выделить Рs и Рm , т.е. критические значения напряжения начала и завершения разрушения структуры. Можно отметить два значения вязкости: в области напряжений (0 – Рs) – вязкость, эффективная для жидкости с неразрушенной структурой, и в области Р > Рm – вязкость ньютоновской жидкости с полностью разрушенной структурой. В промежуточной области напряжений (Рs — Рm) вязкость монотонно уменьшается от величины h0 до hm.
При достижении критического статического напряжения сдвига Рs, необходимого для разрушения твердообразной структуры, образовавшейся в статических условиях, система начинает необратимо деформироваться, и наблюдается пластическое течение с переменной вязкостью вплоть до напряжений Рd,после чего пластическое течение происходит с постоянным динамическим (тиксотропным) восстановлением структуры. Этот участок кривой описывают уравнением Бингама и говорят о бингамовской вязкости дисперсной системы hmin.
На участке Рsk – Рd эффективная (кажущаяся) вязкость изменяется в очень широких пределах, иногда различие составляет два и более порядка. Участок реологической кривой с постоянной вязкостью hmax характерен для, так называемой, шведовской жидкости, которая характеризуется пластично-вязким течением. Уравнение Шведова для описания этого участка имеет вид
P = Ps + h * max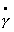
где h * max – пластическая эффективная (шведовская) вязкость. Участок напряжений Рd – Рm характеризуется уравнением Бингама в форме
P = Ps + h * min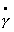
где h * min – пластическая эффективная (бингамовская) вязкость.
Построение полных реологических кривых течения позволяет определить ряд постоянных для описания структурно-механических свойств дисперсных систем.
В области от Рs до Рm эффективная вязкость зависит от доли обратимо (тиксотропно) восстанавливающихся связей между частицами и эта зависимость для жидкообразных структур имеет вид
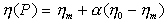
Уравнение (2.4.61) предложил П.А. Ребиндер.
Для твердообразных структур это уравнение будет иметь вид
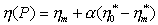
Как показал М. Кросс для жидкообразных структур степень восстановления структуры
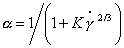
где K = ki / k0 – постоянная относительной скорости разрушения структуры; ki, k0– постоянные скорости разрушения при градиенте скорости, соответственно 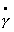
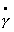
Уравнение (2.4.61) с учетом уравнения (2.4.63) можно привести к линейной форме, если использовать величину, обратную вязкости, т.е. 1/h, называемую текучестью:
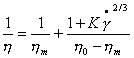
РЕОЛОГИЧЕСКИЕ СВОЙСТВА дисперсных систем. Структурная вязкость.
Структурно-механические свойства изучает реология – наука о деформациях и течении. В реологии механические свойства систем описываются с точки зрения деформаций, возникающих под действием внешних напряжений. В коллоидной химии методы реологии используются для изучения структуры и вязкостных свойств дисперсных систем.
Основными понятиями реологии являются деформация и напряжение. Под деформацией понимают относительное смещение точек системы без нарушения ее сплошности. Различают упругие и остаточные деформации. Упругие деформации обратимы, при упругой деформации после снятия приложенного напряжения структура тела полностью восстанавливается. Остаточные деформации необратимы, после снятия напряжения в структуре системы остаются изменения. Остаточные деформации, не приводящие к разрушению тела, называются пластическими.
Напряжение, под действием которого происходит деформация, определяется как отношение силы к площади, на которую эта сила действует. Напряжения, вызывающие деформации, делятся на нормальные и тангенциальные. Каждому виду напряжений соответствует определенный вид деформации. Нормальные напряжения вызывают деформации растяжения (сжатия), тангенциальные – деформации сдвига. Наиболее важными для реологических исследований являются деформации сдвига, т.к. при этих деформациях проявляются такие важнейшие свойства материальных систем как упругость, пластичность, вязкость и прочность.
П.А. Ребиндер предложил классифицировать структуры, образующиеся в дисперсных системах, по характеру взаимодействия частиц. В соответствии с этим различают конденсационно-кристаллизационные и коагуляционные структуры. При срастании частиц образуются конденсационно-кристаллизационные структуры, обладающие жесткой структурой и высокой прочностью. Коагуляционные структуры образуются в случае контактирования частиц через прослойку дисперсионной среды. Для систем с коагуляционными структурами характерно восстановление структуры во времени после ее механического разрушения. Это явление получило название тиксотропии.
По реологическим свойствам все реальные системы делят на жидкообразные и твердообразные. К жидкообразным системам относятся системы с пределом текучести равным нулю (q = 0), к твердообразным – с q > 0.
Жидкообразные системы делят на ньютоновские и неньютоновские. Ньютоновскими называют системы, подчиняющиеся закону Ньютона. Вязкость ньютоновских жидкостей не зависит от напряжения сдвига.
При перемещении жидкости по узким трубкам отдельные ее слои передвигаются с различными скоростями, возрастающими от стенок к центру (рисунок 5.1). Между слоями текущей жидкости возникает сила внутреннего трения Fтр.равная, согласно закону Ньютона:
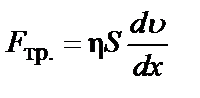
| Рисунок 5.1 – Эпюра скоростей течения в узкой цилиндрической трубке: u – скорость течения жидкости в одном из слоев, u+du – скорость течения жидкости в соседнем слое, находящемся на расстоянии dx от предыдущего |
где S – поверхность соприкосновения трущихся слоев; 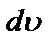
h – коэффициент пропорциональности;
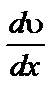
Разделив обе части уравнения (5.1) на площадь S , получим
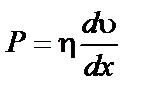
где Р – напряжение сдвига, то есть сила, отнесенная к единице площади поверхности трущихся слоев. При 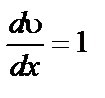
Из уравнения (5.2) вытекает размерность динамической вязкости 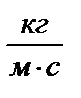
Непосредственное использование закона Ньютона для расчета вязкости затруднительно в силу сложности экспериментального определения градиента скорости. Обычно для этого применяют уравнение Пуазейля для истечения жидкости из узких трубок (капилляров)
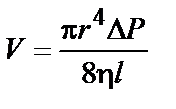
где V – объемная скорость истечения; r – радиус капилляра; 
Уравнения Ньютона и Пуазейля справедливы только для ламинарного режима течения жидкости. Жидкости, подчиняющиеся законам Ньютона и Пуазейля, называются нормальными или ньютоновскими; жидкости, способные течь, но не подчиняющиеся этим уравнениям, принято называть аномальными или неньютоновскими.
Присутствие в жидкости частиц коллоидной степени дисперсности увеличивает вязкость. Связь между вязкостью системы h и концентрацией дисперсной фазы установил, исходя из чисто гидродинамических соображений, Эйнштейн:
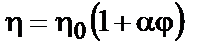
где 
a– константа, зависящая от формы частиц дисперсной фазы (для сферических частиц a= 2,5); j– объемная доля дисперсной фазы в системе.
Уравнение (5.4) применимо только к разбавленным растворам, где частицы не оказывают влияния друг на друга и при условии ламинарного режима течения.
Однако в некоторых случаях даже при сравнительно небольших концентрациях лиофильного золя (например, разбавленные гидрозоли желатина, таннина, 0,0045 % –гидрозоль пятиокиси ванадия, 0,1% раствор бентонита в воде и др.), линейная зависимость, определяемая уравнением (5.4), нарушается, и вязкость оказывается значительно более высокой, чем это следует из уравнения.
Последнее обстоятельство объясняется, во-первых, тем, что эти золи могут легко переходить в гели и в системе появляется пространственная структура. Во-вторых, частицы коллоидов, взаимодействуя с дисперсионной средой, приобретают сольватные оболочки, что ведет к увеличению эффективного объема частиц.
При наличии в системе малопрочной пространственной структуры, способной разрушаться в вискозиметре, течение начинается лишь тогда, когда напряжение сдвига P превысит некоторое определенное критическое значение q, необходимое для. разрушения структуры, то есть, когда будет соблюдаться условие
Такое течение называется пластическим, а критическое (предельное) напряжение сдвига q– пределом текучести. Для таких систем уравнение Ньютона заменяется уравнением Шведова-Бингама
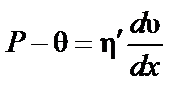
где 
Рисунок 5.2 – Зависимость градиента скорости течения жидкости 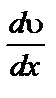 от напряжения сдвига P: 1 – ньютоновская жидкость, 2 – система Шведова-Бингама, 3 – система с прочной пространственной структурой, разрушающейся по мере роста напряжения сдвига сдвига от напряжения сдвига P: 1 – ньютоновская жидкость, 2 – система Шведова-Бингама, 3 – система с прочной пространственной структурой, разрушающейся по мере роста напряжения сдвига сдвига |
Если пространственная структура отсутствует (q = 0), уравнение Шведова-Бингама (5.5) переходит в уравнение (5.2), а пластическая вязкость – в истинную вязкость жидкости.
В структурированных жидкостях течение с постоянной вязкостью начинается, когда напряжение сдвига Р превысит q (прямая 2 в системе координат 
Отсюда пластическая вязкость
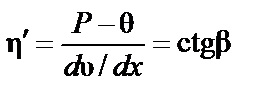
Примером систем, подчиняющихся уравнению Шведова-Бингама, являются пасты из глины (глинистые растворы или промывочные жидкости), консистентные смазки, некоторые краски.
На основе уравнения Шведова-Бингама создана гидравлика глинистых растворов, позволяющая решать важные теоретические и практические задачи, связанные с расчетом потерь напора в циркуляционной системе, правильного подбора насосов и др.
Системы, подчиняющиеся уравнению Шведова-Бингама, называются бингамовскими. Для них характерно явление тиксотропии – изотермического перехода структурированной системы под действием сдвигового напряжения Р в бесструктурную и восстановление структуры после прекращения воздействия сдвигового напряжения.
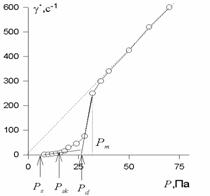
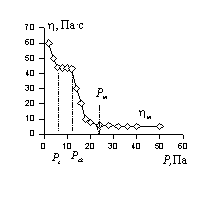
Однако в большинстве случаев зависимость 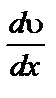
В этом случае различают три критических напряжения сдвига: qmin– минимальный предел текучести, соответствующий началу течения или разрушения структуры; qВ– предел текучести по Шведову-Бингаму; qmах –максимальный предел текучести, соответствующий значению напряжения, при котором кривая переходит в прямую, в этот момент структура полностью разрушена, и система течет как ньютоновская жидкость.
| Рисунок 5.3 – Глинистый буровой раствор как тиксотропная бингамовская система |
Простейший пример бингамовской системы, обладающей тиксотропными свойствами – глинистый буровой раствор. При прокачивании глинистого бурового раствора гидратированные частички глины не связаны друг с другом (рисунок 5.3 a) – глинистый раствор ведет себя какньютоновская жидкость. При остановке прокачивания частички глины самопроизвольно слипаются (при этом уменьшается свободная поверхностная энергия системы), образуется внутренняя структура (pисунок 5.3 b).
| Pисунок 5.4 – Системы с прочной структурой: а) водный раствор КМЦ; b) раствор каучука в толуоле |
Вязкость системы становится бесконечно большой. Этот факт чрезвычайно важен при бурении скважин, так как при этом исключается возможность осаждения выбуриваемой породы на забой скважины. При восстановлении циркуляции структура вновь разрушается (pисунок 5.3 c) и глинистый раствор снова течет как бесструктурная ньютоновская жидкость.
Как уже указывалось, в большинстве случаев структурированные системы изменяются постепенно и только после полного разрушения структуры текут как ньютоновские.
По реологическому поведению к бингамовским системам относятся пульпы, шламы, зубные пасты, масляные краски, пластичные смазки.
В качестве моделей структурированных систем рассмотрим поведение водного раствора КМЦ и толуольного раствора каучука при их продавливании через капилляр вискозиметра.
На рисунке 5.4 a показана модель структуры водного раствора КМЦ, представляющая собой «кучу хвороста», где роль »хвороста» выполняют относительно небольшие макромолекулы КМЦ и структура «клубок ниток» (рисунок 5.4 b), образованная огромными и гибкими по сравнению с КМЦ макромолекулами каучука. Дисперсионной средой в этих системах являются соответственно вода и толуол. При приложении внешнего давления начинается постепенное «разрушение» структуры, выражающееся в упорядочении движения макромолекул. Структура считается разрушенной полностью, когда макромолекулы при их протекании через капилляр начинают двигаться упорядоченно, располагаясь вдоль оси капилляра – в этот момент указанные системы ведут себя как ньютоновские жидкости.
Вязкость жидкостей и дисперсных систем определяют различными методами: а) методом падающего шарика (вискозиметр Гепплера); б) методом истечения жидкости из капилляра (вискозиметр Оствальда, вискозиметр СПВ-5, используемый в нефтепромысловой практике); в) методом определения вязкостных характеристик с помощью ротационных и торсионных вискозиметров (вискозиметры Куэтта, Воларовича, СНС-2, Реотест-2 и др.).
При работе с капиллярным вискозиметром имеется простой способ выяснения вопроса, является ли исследуемая жидкость ньютоновской или неньютоновской. Для этого избыточное давление,под которым вытекает жидкость, умножают на соответствующее время истечения.
Представим уравнение Пуазейля в виде:

Если произведение 
Вязкость жидкостей существенно зависит от температуры. Для большинства жидкостей зависимость вязкости от температуры при постоянном давлении в узком интервале температур может быть описана уравнением:
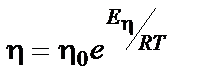
где h0 – предэкспоненциальный множитель, слабо зависящий от температуры; Еh – энергия активации вязкого течения.
Учитывая сильную зависимость вязкости жидкостей от температуры, эксперименты по изучению их реологического поведения проводят в условиях термостатирования исследуемой системы.
Лабораторная работа 5.1
http://xumuk.ru/colloidchem/132.html
http://megalektsii.ru/s23480t7.html