Решаем уравнение методом разложения на множители

Решение уравнений методом разложения на множители

Решение уравнений разложения на множители (метод расщепления) – это способ решения уравнений при котором мы стремимся уравнение свести их к виду:

а затем каждую скобку приравнять к нулю и решить как отдельное уравнение.

Вынесем за скобку икс.

Разобьем уравнение на два простейших.

В первом корень уравнения уже понятен, во втором надо перенести \(5\) в правую сторону.

Решение методом разложения на множители основывается на простой идее:

В результате умножения ноль можно получить, только если один из множителей равен нулю.

Попробуйте придумать два числа, которые при умножении дают ноль. Вы убедитесь, что хотя бы одно из них обязательно должно быть нулем.

Этот метод решения уравнений один из самых популярных, поэтому освоить его очень важно для тех, кто планирует иметь четверки и пятерки. А для освоения этого метода, конечно, надо уметь раскладывать на множители как Бог: знать все формулы сокращенного умножения, легко выносить множители за скобки, уметь применять метод группировки и т.д. Подробнее о всех способах разложения на множители смотри здесь .

Пример(задание из ОГЭ). Решите уравнение \(x^3+4x^2-4x-16=0\).
Решение:

Перед нами кубическое уравнение.
Применим метод группировки: из первой пары слагаемых вынесем \(x^2\), а из второй – минус четверку.

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №12. Решение алгебраических уравнений разложением на множители.

Перечень вопросов, рассматриваемых в теме

1) типы алгебраических уравнений;

2) решение алгебраические уравнения методом разложения на множители;

3) методы решения алгебраических уравнений.

Глоссарий по теме

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x₁, x₂, …, x_n)=0, где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнение над множеством F.

Степенью алгебраического уравнения называют степень многочлена P.

Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Биквадратными называются уравнения вида ах 4 + bх 2 + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.

Симметрическим уравнением 3-ей степени называют уравнение вида: ax 3 + bx 2 + bx + a = 0, где a, b – заданные числа.

Уравнение вида a n x n ₊a n-1 x n-1 +…+a 1 x+a 0 =0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. a n-1 =a k , при k=0, 1, …, n.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Давайте вспомним, что такое алгебраическое уравнение?

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x₁, x₂, …, x_n)=0, где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого поля F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнение над полем F.

Степенью алгебраического уравнения называют степень многочлена P.

является алгебраическим уравнением седьмой степени от трёх переменных (с тремя неизвестными) над полем вещественных чисел.

Связанные определения. Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Примеры и разбор решения заданий тренировочного модуля

1. Алгебраические уравнения, решаемые разложением на множители:

D(–2) : ,

Можно догадаться, что число х₁ = –1 является корнем этого уравнения, так как –1 + 3 – 2 = 0.

х + 1 = 0 или х 2 –х–2 = 0;

х₁ = –1 х_2,3 = ;

х_2,3 = ;

x 3 + х 2 – х 2 – х – 2x – 2 = 0;

(x 3 + х 2 ) – (х 2 + х) – 2(x + 1) = 0;

х 2 (х + 1) – х(х + 1) – 2(х + 1) = 0;

(х + 1) (х + 1) (х –2) = 0;

(х –2) = 0;

1. Уравнения, сводящиеся к алгебраическим
   1. Биквадратные уравнения

На прошлом уроке мы познакомились с данным видом уравнений

Определение. Биквадратными называются уравнения вида ах 4 + bх 2 + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.

Метод решения

Биквадратное уравнение приводится к квадратному уравнению при помощи подстановки у=х 2 .

Новое квадратное уравнение относительно переменной у: ay 2 +by+c=0.

Решая это уравнение, мы получаем корни квадратного уравнения

Решая эти два уравнения (y₁=x₁ 2 и y₂=x₁ 2 ) относительно переменной x, мы получаем корни данного биквадратного уравнения.

Порядок действий при решении биквадратных уравнений

1. Ввести новую переменную у=х 2
2. Подставить данную переменную в исходное уравнение
3. Решить квадратное уравнение относительно новой переменной
4. После нахождения корней (y₁; y₂) подставить их в нашу переменную у=х 2 и найти исходные корни биквадратного уравнения

х 4 – 8х 2 – 9 = 0.

Решение: Пусть у = х 2 , где у 0; у 2 – 8у – 9 = 0;

По формулам Виета:

Первое решение отбрасываем ( у 0),

а из второго находим х₁ = –3; х₂ = 3.

2 Симметрические уравнения

Решение симметрических уравнений рассмотрим на примере симметрических уравнений третьей степени.

Симметрическим уравнением 3-ей степени называют уравнение вида ax 3 + bx 2 + bx + a = 0, где a, b – заданные числа.

Для того, чтобы успешно решать уравнения такого вида, полезно знать и уметь использовать следующие простейшие свойства симметрических уравнений:

1 0 . У любого симметрического уравнения нечетной степени всегда есть корень, равный -1.

Действительно, если сгруппировать в левой части слагаемые следующим образом: а(х 3 + 1) + bx(х + 1) = 0, то есть возможность вынести общий множитель, т.е.

(х + 1)(ах 2 + (b – а)x + а) = 0, поэтому,
х + 1 = 0 или ах 2 + (b – а)x + а = 0,

первое уравнение и доказывает интересующее нас утверждение.

2 0 . У симметрического уравнения корней, равных нулю, нет.

3 0 . При делении многочлена нечетной степени на (х + 1) частное является снова симметрическим многочленом.

х 3 + 2x 2 + 2х + 1 = 0.

Решение: У исходного уравнения обязательно есть корень х = –1.

Разлагая далее левую часть на множители, получим

(х + 1)(x 2 + х + 1) = 0.

x 2 + х + 1 = 0 не имеет корней.

2 Возвратные уравнения

Уравнение вида a n x n ₊a n-1 x n-1 +…+a 1 x+a 0 =0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. a n-1 =a k , при k=0, 1, …, n.

Рассмотрим возвратное уравнение четвёртой степени вида

ax⁴ + bx³ + cx² + bx + a = 0, где a, b и c — некоторые числа, причём a ≠ 0. Оно является частным случаем уравнения ax⁴ + bx³ + cx² + kbx + k²a = 0 при k = 1.

Порядок действий при решении возвратных уравнений вида ax 4 + bx 3 + cx 2 + bx + a = 0:

• разделить левую и правую части уравнения на . При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения;
• группировкой привести полученное уравнение к виду

• ввести новую переменную , тогда выполнено
  , то есть ;

в новых переменных рассматриваемое уравнение является квадратным: at 2 +bt+c–2a=0;

• решить его относительно t, возвратиться к исходной переменной.

Решение: Разделим на x 2 , получим:

Введем замену:
Пусть

Метод разложения на множители при решении иррациональных уравнений

Продолжаем знакомиться с методами решения иррациональных уравнений. В этой статье мы детально разберем, как используется метод разложения на множители при решении иррациональных уравнений. Материал представим так: кратко напомним основные положения метода, после чего будем подробно разбирать решения характерных иррациональных уравнений методом разложения на множители.

Основные положения метода разложения на множители

В статье метод разложения на множители очень подробно разобрана вся соответтвующая теория. Здесь мы не будем ее полностью повторять, а перечислим лишь основные положения и запишем алгоритм метода разложения на множители. Просто удобно, если он будет перед глазами, когда мы перейдем к решению примеров.

Метод разложения на множители применяется для решения уравнений, в левых частях которых находится некоторое произведение, а в правых – нули, то есть, для решения уравнений вида f₁(x)·f₂(x)·…·f_n(x)=0 , где f₁, f₂, …, f_n – некоторые функции. Суть метода состоит в замене уравнения f₁(x)·f₂(x)·…·f_n(x)=0 совокупностью уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0 на ОДЗ переменной x для исходного уравнения.

Первая часть последнего предложения про переход к совокупности следует из известного с начальной школы факта: произведение нескольких чисел тогда и только тогда равно нулю, когда хотя бы одно из чисел равно нулю. Наличие второй части про ОДЗ объясняется тем, что переход от уравнения f₁(x)·f₂(x)·…·f_n(x)=0 к совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0 может быть неравносильным и приводить к появлению посторонних корней, от которых в данном случае позволяет избавиться учет ОДЗ. Стоит отметить, что отсеивание посторонних корней, если это удобно, может быть проведено не только через ОДЗ, но и другими способами, например, проверкой через подстановку найденных корней в исходное уравнение.

Итак, чтобы решить уравнение f₁(x)·f₂(x)·…·f_n(x)=0 методом разложения на множители, в том числе и иррациональное, нужно

• Перейти к совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0 ,
• Решить составленную совокупность,
• Если совокупность решений не имеет, то сделать вывод об отсутствии корней у исходного уравнения. Если же корни есть, то отсеять посторонние корни.

Переходим к практической части.

Примеры решения характерных иррациональных уравнений

Левые части типичных иррациональных уравнений, которые решаются методом разложения на множители, представляют собой произведения нескольких алгебраических выражений, обычно линейных двучленов и квадратных трехчленов, и нескольких корней с алгебраическими выражениями под ними. В правых частях нули. Такие уравнения идеальны для получения начальных навыков использования метода разложения на множители для решения иррациональных уравнений. С решения подобного уравнения начнем и мы. При этом попробуем достичь двух целей:

• разобрать все шаги алгоритма,
• вспомнить три основных способа отсеивания посторонних корней (по ОДЗ, по условиям ОДЗ и при помощи непосредственной подстановки решений в исходное уравнение).

Решить иррациональное уравнение

Следующее иррациональное уравнение 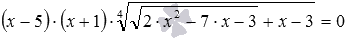типично в том плане, что при его решении методом разложения на множители отсеивание посторонних корней удобно проводить по условиям ОДЗ, а не по ОДЗ в виде числового множества, так как получить ОДЗ в виде числового множителя затруднительно. Сложность в том, что одно из условий, определяющих ОДЗ, представляет собой иррациональное неравенство . Указанный подход к отсеиванию посторонних корней позволяет обойтись без его решения, более того, иногда в школьном курсе математики вообще не знакомятся с решением иррациональных неравенств.

Решить уравнение

Хорошо, когда уравнение имеет в левой части произведение, а в правой – ноль. В этом случае сразу можно переходить к совокупности уравнений, решить ее, найти и отбросить посторонние для исходного уравнения корни, что даст искомое решение. Но чаще уравнения имеют иной вид. Если при этом просматривается возможность преобразовать их к виду, подходящему для применения метода разложения на множители, то почему бы не попробовать провести соответствующие преобразования. Например, чтобы получить произведение в левой части следующего иррационального уравнения, достаточно прибегнуть к формуле сокращенного умножения разность квадратов.

Решить иррациональное уравнение

Есть еще один класс уравнений, которые обычно решают методом разложения на множители. К нему относятся уравнения, обе части которых являются произведениями, имеющими одинаковый множитель в виде выражения с переменной. Таково, например, иррациональное уравнение . Можно пойти путем деления обеих частей уравнения на одинаковый множитель, но при этом нельзя забывать отдельно проверять значения, обращающие в нуль это выражения, иначе можно потерять решения, ведь деление обеих частей уравнения на одно и то же выражение может быть неравносильным преобразованием. Надежнее действовать по методу разложения на множители, это позволяет гарантированно избежать потери корней при дальнейшем корректном решении. Понятно, что для этого надо сначала получить в левой части уравнения произведение, а в правой части получить ноль. Это легко: достаточно перенести выражение из правой части в левую, изменив его знак, и вынести общий множитель за скобки. Покажем полное решение подобного, но чуть более сложного иррационального уравнения.

Решить уравнение

Решение любого уравнения (как, впрочем, и решение многих других задач) полезно начинать с нахождения ОДЗ, особенно если ОДЗ находится легко. Приведем несколько самых очевидных доводов в пользу этого.

• Довольно часто требуется проводить какие-либо преобразования уравнения (как, например, в предыдущем примере), а они, как известно, проводятся на ОДЗ.
• Во многих случаях так и так приходится находить ОДЗ, так как это является неотъемлемой частью алгоритма выбранного метода решения, так почему бы не найти ОДЗ сразу. Например, последний шаг алгоритма метода разложения на множители состоит в отсеивании посторонних корней, что удобно делать, используя ОДЗ.
• А иногда ОДЗ позволяет сразу сделать вывод об отсутствии корней или ограничить круг поиска корней несколькими числами. Это относится к случаям, когда ОДЗ есть пустое множество или множество, представляющее собой некоторое количество чисел. Подробнее об этом поговорим в отдельной статье решение иррациональных уравнений через ОДЗ.

Итак, получив задание решить уравнение, не стоит без оглядки бросаться в преобразования-вычисления, может достаточно взглянуть на ОДЗ? Это ярко демонстрирует следующее иррациональное уравнение.

Решите иррациональное уравнение

На этом можно считать, что мы освоили решение иррациональных уравнений методом разложения на множители. Можно двигаться дальше: начинать разбирать графический метод решения иррациональных уравнений.