Решебник показательных уравнений и неравенств

Решебник показательных уравнений и неравенств

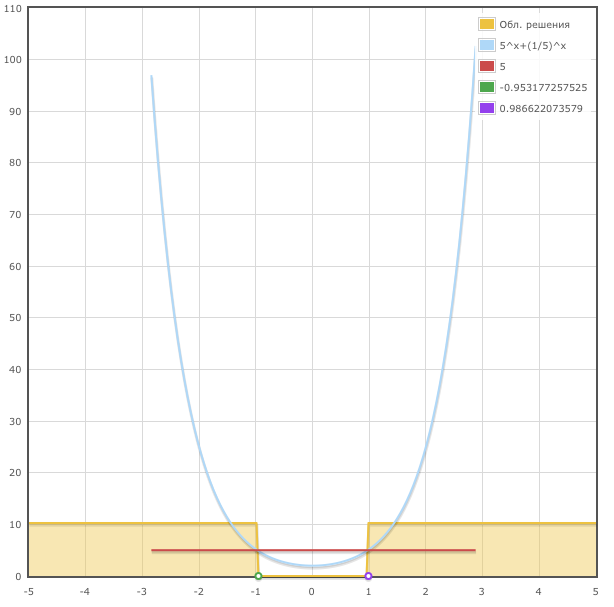
>>решение неравенств онлайн 5$$ Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние: $$5^ + \left(\frac<1><5>\right)^ = 5$$ Решаем:
Дано уравнение: $$5^ + \left(\frac<1><5>\right)^ = 5$$ или $$5^ + \left(\frac<1><5>\right)^ — 5 = 0$$ Сделаем замену $$v = \left(\frac<1><5>\right)^$$ получим $$v — 5 + \frac<1> = 0$$ или $$v — 5 + \frac<1> = 0$$ делаем обратную замену $$\left(\frac<1><5>\right)^ = v$$ или $$x = — \frac<\log<\left (v \right )>><\log<\left (5 \right )>>$$ $$x_ <1>= \frac<1><\log<\left (5 \right )>> \left(- \log <\left (2 \right )>+ \log <\left (\sqrt<21>+ 5 \right )>\right)$$ $$x_ <2>= \frac<1><\log<\left (5 \right )>> \left(\log <\left (- \sqrt<21>+ 5 \right )> — \log<\left (2 \right )>\right)$$ $$x_ <1>= \frac<1><\log<\left (5 \right )>> \left(- \log <\left (2 \right )>+ \log <\left (\sqrt<21>+ 5 \right )>\right)$$ $$x_ <2>= \frac<1><\log<\left (5 \right )>> \left(\log <\left (- \sqrt<21>+ 5 \right )> — \log<\left (2 \right )>\right)$$ Данные корни $$x_ <2>= \frac<1><\log<\left (5 \right )>> \left(\log <\left (- \sqrt<21>+ 5 \right )> — \log<\left (2 \right )>\right)$$ $$x_ <1>= \frac<1><\log<\left (5 \right )>> \left(- \log <\left (2 \right )>+ \log <\left (\sqrt<21>+ 5 \right )>\right)$$ являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки: $$x_ <0>5$$

значит одно из решений нашего неравенства будет при:
$$x \frac<1><\log<\left (5 \right )>> \left(- \log <\left (2 \right )>+ \log <\left (\sqrt<21>+ 5 \right )>\right)$$

Также вы будете иметь графическое решение показательного неравенства:

Тэги: неравенство

© Контрольная работа РУ — примеры решения задач

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение показательных неравенств.

Этот математический калькулятор онлайн поможет вам решить показательное неравенство. Программа для решения показательного неравенства не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите показательное неравенство
Решить неравенство

Немного теории.

Показательные неравенства

Неравенства вида
\( a^x > b \) и \( a^x 0, \; a \neq 0, \; b \in \mathbb \)
называют простейшими показательными неравенствами.

Напомним, что решением неравенства называют число \(x_0\), при подстановке которого в неравенство получается верное числовое неравенство.

Решить неравенство — значит найти все его решения или показать, что их нет.

Случай \( b \leqslant 0\)

Поскольку \( a^x >0 \) для любого \( x \in \mathbb \), то при \( b \leqslant 0\) неравенство \( a^x > b \) верно для любого \( x \in \mathbb \).
И нет ни одного \( x \in \mathbb \) для которого было бы верно неравенство \( a^x \leqslant b \) при \( b \leqslant 0\).

Таким образом, если \( b \leqslant 0\), то множество всех решений неравенства \( a^x > b \) есть интервал \( (-\infty; \; +\infty) \), а неравенство \( a^x 0\)

Если же \( b > 0\), то исходные неравенства можно переписать в виде
\( a^x > a^c \) и \( a^x 1\)

Рассмотрим решение неравенств \( a^x > a^c \) и \( a^x 1\)
Так как для такого \(a\) функция \( y = a^x \) является возрастающей, то для любого числа \( x > c \) верно неравенство \( a^x > a^c \), а для любого числа \( x 0\) и \( a > 1\) множество всех решений неравенства \( a^x > a^c \) есть интервал \( (c; \; +\infty) \), а множество всех решений неравенства \( a^x c \) верно неравенство \( a^x a^c \).
Кроме того, равенство \( a^x = a^c \) справедливо лишь при \( x = c \).

Таким образом, при \( b > 0\) и \( 0 a^c \) есть интервал \( (-\infty; \; c) \), а множество всех решений неравенства \( a^x 0, то неравенство можно переписать в виде \(2x 1, то функция \(y = 2^x\) возрастающая. Поэтому решением неравенства, являются все x 0, то это неравенство можно переписать в виде
$$ \left( \frac<1><3>\right)^x log_<\frac<1><3>>5 \)
Ответ: \( (log_<\frac<1><3>>5 ; \; +\infty) \)

ПРИМЕР 3. Решим неравенство \( 2^ + 2^

Показательные уравнения и неравенства с примерами решения

Содержание:

Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:

Уравнения такого вида принято называть показательными.

Решении показательных уравнений

При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.

Пусть

Каждому значению показательной функции соответствует единственный показатель s.

Пример:

Решение:

Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению

Пример:

Решение:

а) Данное уравнение равносильно (поясните почему) уравнению

Если степени с основанием 3 равны, то равны и их показатели:

Решив это уравнение, получим

Ответ:

При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.

Пример:

Решение:

а) Данное уравнение равносильно уравнению

Решая его, получаем:

Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. откуда находим

б) Разделив обе части уравнения на получим уравнение равносильное данному. Решив его, получим

Ответ:

При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.

Пример:

Решить уравнение

Решение:

Обозначим тогда

Таким образом, из данного уравнения получаем

откуда находим:

Итак, с учетом обозначения имеем:

При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.

Пример:

Решить уравнение

Решение:

Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).

Пример:

Решить уравнение

Решение:

Пример:

При каком значении а корнем уравнения является число, равное 2?

Решение:

Поскольку х = 2 — корень, то верно равенство

Решив это уравнение, найдем

Ответ: при

Показательные уравнения и их системы

Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:

Приведем методы решения некоторых типов показательных уравнений.

1 Приведение к одному основанию.

Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду . Отсюда

Пример №1

Решите уравнение

Решение:

Заметим, что и перепишем наше уравнение в виде

Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1.

Пример №2

Решить уравнение

Решение:

Переходя к основанию степени 2, получим:

Согласно тождеству (2), имеем

Последнее уравнение равносильно уравнению 4х-19 = 2,5х.

2 Введение новой переменной.

Пример №3

Решить уравнение

Решение:

Применив тождество 2, перепишем уравнение как

Введем новую переменную: Получим уравнение

которое имеет корни Однако кореньне удовлетворяет условию Значит,

Пример №4

Решить уравнение

Решение:

Разделив обе части уравнения на получим:

последнее уравнение запишется так:

Решая уравнение, найдем

Значение не удовлетворяет условию Следовательно,

Пример №5

Решить уравнение

Решение:

Заметим что Значит

Перепишем уравнение в виде

Обозначим Получим

Получим

Корнями данного уравнения будут

Следовательно,

III Вынесение общего множителя за скобку.

Пример №6

Решить уравнение

Решение:

После вынесения за скобку в левой части , а в правой , получим Разделим обе части уравнения на получим

Системы простейших показательных уравнений

Пример №7

Решите систему уравнений:

Решение:

По свойству степеней система уравнений равносильна следующей

системе :Отсюда получим систему

Очевидно, что последняя система имеет решение

Пример №8

Решите систему уравнений:

Решение:

По свойству степеней система уравнений равносильна следующей системе: Последняя система, в свою очередь, равносильна системе:

Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем Подставив полученное значение во второе уравнение, получим

Пример №9

Решите систему уравнений:

Решение:

Сделаем замену: Тогда наша система примет вид:

Очевидно, что эта система уравнений имеет решение

Тогда получим уравнения

Приближенное решение уравнений

Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть . Тогда внутри этого отрезка существует хотя бы одно решение уравнения Дх)=0. Это означает, что существует такое (читается как «кси»), что

Это утверждение проиллюстрировано на следующем чертеже.

Рассмотрим отрезок содержащий лишь один корень уравнения .

Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности

1. вычисляется значение f(х) выражения
2. отрезок делится пополам, то есть вычисляется значение
3. вычисляется значение выражения f(х) в точке
4. проверяется условие
5. если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что (левый конец отрезка переходит в середину);
6. если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
7. для нового отрезка проверяется условие
8. если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.

Метод последовательного деления пополам проиллюстрирован на этом чертеже:

Для нахождения интервала, содержащего корень уравнения вычисляются значения

Оказывается, что для корня данного уравнения выполнено неравенство. Значит, данное уравнение имеет хотя бы один корень, принадлежащий интервалу (-1 -А; 1+А). Для приближенного вычисления данного корня найдем целые и удовлетворяющие неравенству

Пример №10

Найдите интервал, содержащий корень уравнения

Решение:

Поделив обе части уравнения на 2 , получим,

Так как, для нового уравнения

Значит, в интервале, уравнение имеет хотя бы один корень. В то же время уравнение при не имеет ни одного корня, так как,

выполняется. Значит, корень уравнения лежит в (-2,5; 0). Для уточнения этого интервала положим Для проверим выполнение условия

Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).

Нахождение приближенного корня с заданной точностью

Исходя из вышесказанного, заключаем, что если выполнено неравенство корень уравнения принадлежит интервалу

ПустьЕсли приближенный

корень уравнения с точностью . Если то корень лежит в интервале если то корень лежит в интервале . Продолжим процесс до нахождения приближенного значения корня с заданной точностью.

Пример №11

Найдите приближенное значение корня уравнения с заданной точностью

Решение:

Из предыдущего примера нам известно, что корень лежит в интервале

(-1; 0). Из того, что заключаем, что корень лежит в интервале (-0,5; 0).

Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| 1. Если

Пусть

Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.