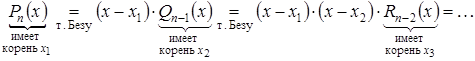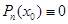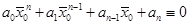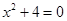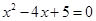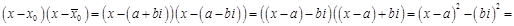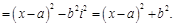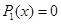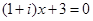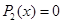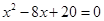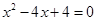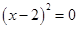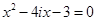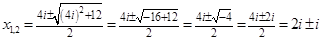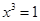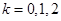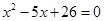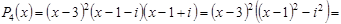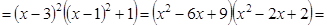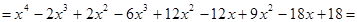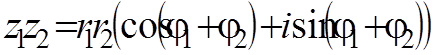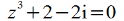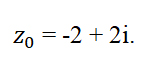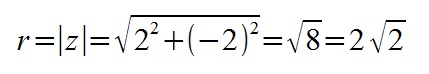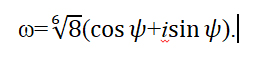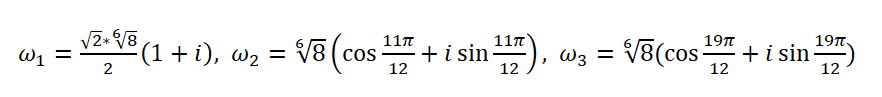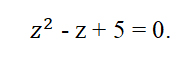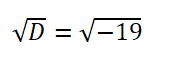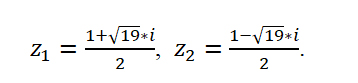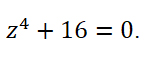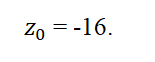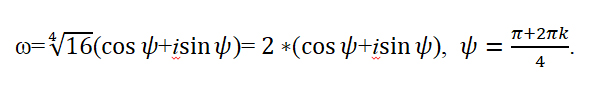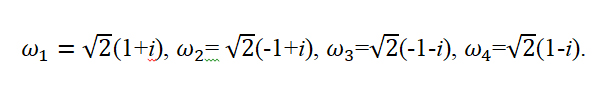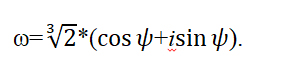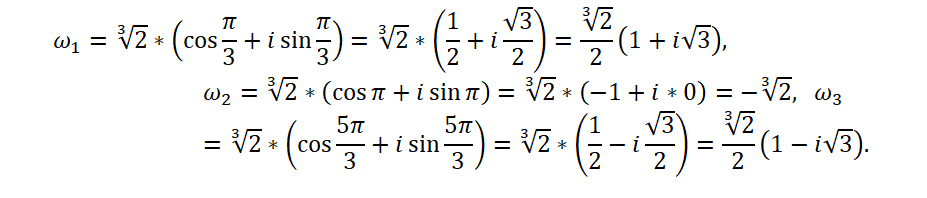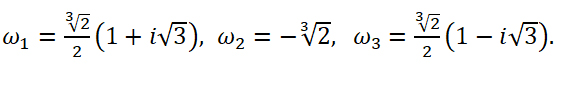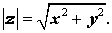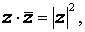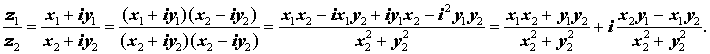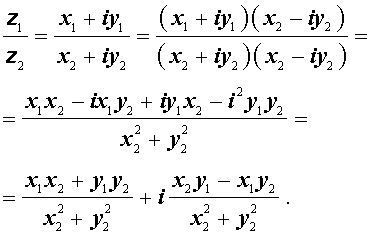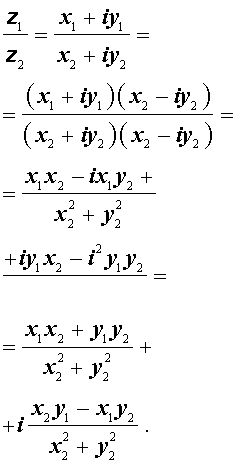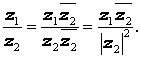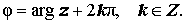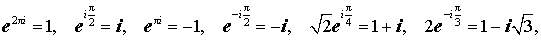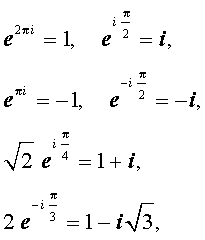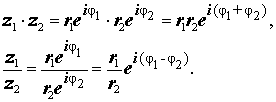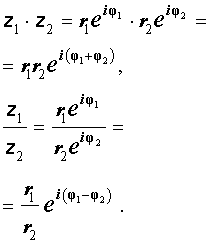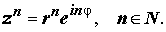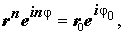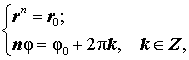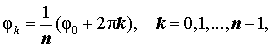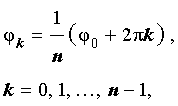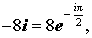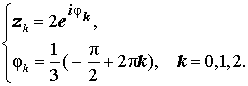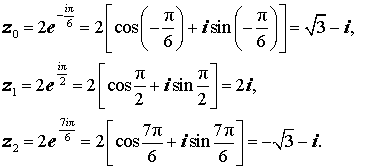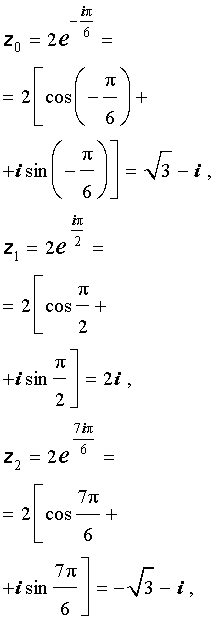Учебное пособие: Комплексные числа
| Название: Комплексные числа Раздел: Рефераты по математике Тип: учебное пособие Добавлен 13:49:20 12 июня 2011 Похожие работы Просмотров: 45866 Комментариев: 26 Оценило: 7 человек Средний балл: 4.3 Оценка: 4 Скачать | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| _ | 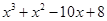 | 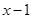 | _ | 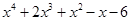 | 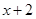 | |||||||||
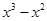 | 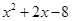 | 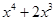 | 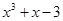 | |||||||||||
| _ | 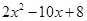 | _ | 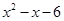 | |||||||||||
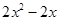 | 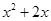 | |||||||||||||
| _ | 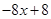 | 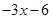 | ||||||||||||
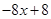 | 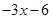 | |||||||||||||
 |  | |||||||||||||
Всякий многочлен степени n ³ 1 имеет, по крайней мере, один нуль, действительный или комплексный
Доказательство этой теоремы выходит за рамки нашего курса. Поэтому примем теорему без доказательства.
Поработаем по этой теореме и по теореме Безу с многочленом Pn (x ).
После n -кратного применения этих теорем получим, что
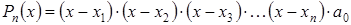
гдеa 0 — это коэффициент при x n в Pn (x ).
Следствие из основной теоремы алгебры. О разложении многочлена на линейные множители
Любой многочлен степени 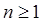

гдех1, х2, … хn — это нули многочлена.
При этом если k чисел из набора х 1, х 2, … хn совпадают между собой и с числом a, то в произведении (6) получается множитель (x – a)k . Тогда число x = a называется k-кратным нулем многочлена Pn ( x ) . Если k = 1, то нуль называется простым нулем многочлена Pn ( x ) .
1)P 4(x ) = (x – 2)(x – 4)3 Þx 1 = 2 — простой нуль, x 2 = 4 — трехкратный нуль;
Свойство 4 (о количестве корней алгебраического уравнения)
Любое алгебраическое уравнение Pn(x) = 0 степени n имеет на множестве комплексных чисел ровно n корней, если считать каждый корень столько раз, какова его кратность.
1)x 2 – 4x + 5 = 0 — алгебраическое уравнение второй степени
Þx 1,2 = 2 ± 
2)x 3 + 1 = 0 — алгебраическое уравнение третьей степени
Þx 1,2,3 = 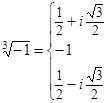
Разделим многочлен P 3(x ) на (x – 1):
| x 3 | + | x 2 | – | x | – | 1 | x – 1 |
| x 3 | – | x 2 | x 2 + 2x +1 | ||||
| 2x 2 | – | x | |||||
| 2x 2 | – | 2x | |||||
| x | – | 1 | |||||
| x | – | 1 | |||||
| 0 |
Þx 1 = 1 — простой корень, x 2 = –1 — двукратный корень.
Если алгебраическое уравнение с действительными коэффициентами имеет комплексные корни, то эти нули всегда парные комплексно сопряженные, то есть если x 0 = a + bi является корнем уравнения Pn (x ) = 0, то число 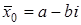
w нужно использовать определение и следующие легко проверяемые свойства операции комплексного сопряжения:
если 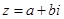
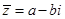
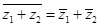
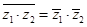
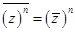
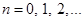
если 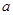
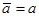
Так как 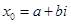
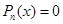
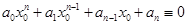
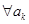
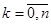
Возьмем сопряжение от обеих частей последнего равенства и используем перечисленные свойства операции сопряжения:
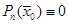
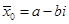
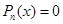
1) 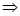
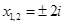
2) 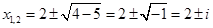
Любой многочлен с действительными коэффициентами разлагается на произведение линейных и квадратичных функций с действительными коэффициентами.
w Пусть x 0 = a + bi — нуль многочлена Pn (x ). Если все коэффициенты этого многочлена являются действительными числами, то 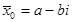
Вычислим произведение двучленов 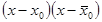
комплексный число многочлен уравнение
Получили (x – a )2 + b 2 — квадратный трехчленс действительными коэффициентами.
Таким образом, любая пара двучленов с комплексно сопряженными корнями в формуле (6) приводит к квадратному трехчлену с действительными коэффициентами. v
Примеры решения алгебраических уравнений на множестве комплексных чисел (Приведите примеры решения алгебраических уравнений на множестве комплексных чисел )
1. Алгебраические уравнения первой степени:
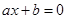
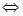
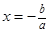
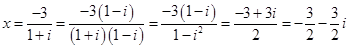
Ответ: 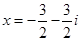
2. Квадратные уравнения:
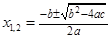
1) 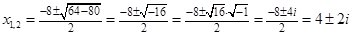
Ответ: 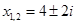
2) 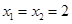
Ответ: 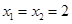
3) 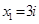
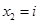
Ответ: 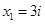
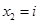
3. Двучленные уравнения степени 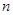
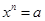
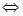
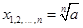
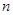
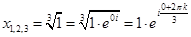
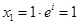
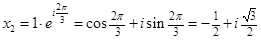
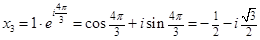
Ответ: 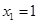
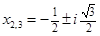
4. Решить кубическое уравнение 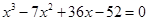
Уравнение третьей степени 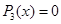
Подбором находим первый корень уравнения 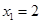
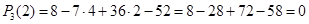
По следствию из теоремы Безу 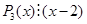
| _ | 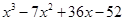 |  | |||
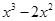 | 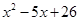 | ||||
| _ | 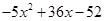 | ||||
 | |||||
| _ | 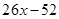 | ||||
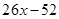 | |||||
 | |||||
Представляя теперь многочлен 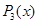
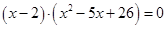
Другие корни находим как корни квадратного уравнения:
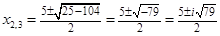
Ответ: 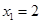
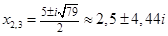
5. Составить алгебраическое уравнение наименьшей степени с действительными коэффициентами, если известно, что числа x 1 = 3 и x 2 = 1 + i являются его корнями, причем x 1 является двукратным корнем, а x 2 — простым.
Число 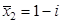
Всего искомое уравнение имеет 4 корня: x 1, x 1, x 2, 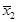
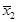
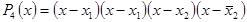
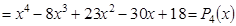
Искомое уравнение имеет вид P 4(x ) = 0.
Ответ: 
1. Сформулируйте определение комплексного числа
3. Какое название или смысл имеет формула?
4. Поясните смысл обозначений в этой формуле:
5. ⌂ 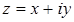
7. Что такое действительная часть комплексного числа z?
9. Что такое комплексно сопряженное число?
11. Что такое комплексный ноль?
13. Сформулируйте смысл комплексного равенства.
15. Что такое модуль и аргумент комплексного числа?
17. Что такое аргумент комплексного числа?
18. Какое название или смысл имеет формула?
19. Поясните смысл обозначений в этой формуле:
20. ⌂ 
21. Что такое алгебраическая и тригонометрическая формы комплексного числа?
22. Какое название или смысл имеет формула?
23. Поясните смысл обозначений в этой формуле:
24. ⌂ 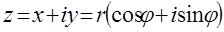
25. Что называется алгебраической формой комплексного числа?
27. Дайте определения и перечислите основные свойства арифметических действий над комплексными числами.
28. Какое название или смысл имеет формула?
29. Поясните смысл обозначений в этой формуле:
31. Какое название или смысл имеет формула?
32. Поясните смысл обозначений в этой формуле:
33. ⌂ 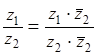
34. Какое название или смысл имеет формула?
35. Поясните смысл обозначений в этой формуле:
36. ⌂ 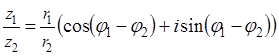
37. Что такое формула Муавра?
38. Какое название или смысл имеет формула?
39. Поясните смысл обозначений в этой формуле:
40. ⌂ 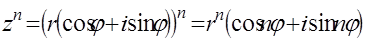
41. Что называется корнем степени n из комплексного числа?
42. Какое название или смысл имеет формула?
43. Поясните смысл обозначений в этой формуле:
44. ⌂ 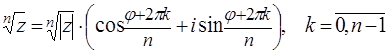
45. Что называется показательной формой комплексного числа?
46. Какое название или смысл имеет формула?
47. Поясните смысл обозначений в этой формуле:
48. ⌂ 
49. Что такое формулы Эйлера?
50. Какое название или смысл имеет формула?
51. Поясните смысл обозначений в этой формуле:
52. ⌂ 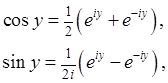
53. Что называется целой функцией?
55. Что называется полиномом?
57. Что такое коэффициенты многочлена?
59. Что называется нулем функции?
61. Перечислите основные свойства многочленов.
63. Сформулируйте свойство о делении многочлена на разность (x – х0).
64. Сформулируйте теорему теорема Безу .
65. Какое название или смысл имеет формула?
66. Поясните смысл обозначений в этой формуле:
67. ⌂ 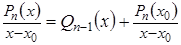
69. Сформулируйте теорему теорема алгебры основная.
70. Какое название или смысл имеет формула?
71. Поясните смысл обозначений в этой формуле:
72. ⌂ 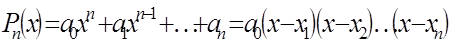
73. Что называется k-кратным нулем многочлена?
75. Сформулируйте свойство о количестве корней алгебраического уравнения.
78. Сформулируйте свойство о разложении многочлена с действительными коэффициентами на линейные и квадратичные множители.
k-кратным нулем многочлена называется. (стр. 18)
алгебраическим многочленом называется. (стр. 14)
алгебраическим уравнением n-й степени называется. (стр. 14)
алгебраической формой комплексного числа называется. (стр. 5)
аргумент комплексного числа это. (стр. 4)
действительная часть комплексного числа z это. (стр. 2)
комплексно сопряженное число это. (стр. 2)
комплексный ноль это. (стр. 2)
комплексным числом называется. (стр. 2)
корнем степени n из комплексного числа называется. (стр. 10)
корнем уравнения называется. (стр. 14)
коэффициенты многочлена это. (стр. 14)
мнимая единица это. (стр. 2)
мнимая часть комплексного числа z это. (стр. 2)
модулем комплексного числа называется. (стр. 4)
нулем функции называется. (стр. 14)
показательной формой комплексного числа называется. (стр. 11)
полиномом называется. (стр. 14)
простым нулем многочлена называется. (стр. 18)
противоположное число это. (стр. 2)
степень многочлена это. (стр. 14)
тригонометрической формой комплексного числа называется. (стр. 5)
Решение уравнений с комплексными числами
Итак, необходимо решить уравнение с комплексными переменными, найти корни этого уравнения. Рассмотрим принцип решения комплексных уравнений, научимся извлекать корень из комплексного числа.
Для того, чтобы решить уравнение n-й степени с комплексными числами, используем общую формулу:
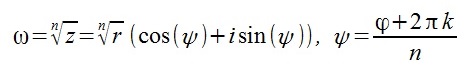
где |z| — модуль числа, φ = arg z — главное значение аргумента, n — степень корня, k — параметр, принимает значения : k = <0, 1, 2, 3, …n-1 >.
Пример 1. Найти все корни уравнения
Выразим z из уравнения:
Все корни заданного уравнения являются значениями корня третьей степени из комплексного числа
Воспользуемся общей формулой для вычисления корней степени n комплексного числа z. Найдем все необходимые значения для формулы:
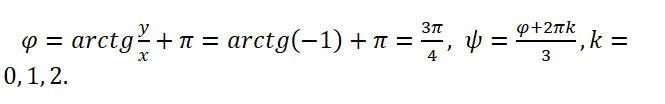
Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения.
Пример 2. Найти все корни уравнения
Найдем дискриминант уравнения:

Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта:
Найдем корни уравнения:

Ответ:
Пример 3. Найти все корни уравнения
Выразим z из уравнения:
Все корни заданного уравнения являются значениями корня четвертой степени из комплексного числа
Вновь используем общую формулу для нахождения корней уравнения n степени комплексного числа z.
n = 4 — количество корней данного уравнения. k = <0, 1, 2, 3>. Найдем модуль комплексного числа:
Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2, 3 найдем все 4 корня уравнения:
Пример 4. Найти корни уравнения
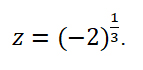
Решение кубического уравнения комплексными числами:
Воспользуемся общей формулой для вычисления корней степени 3 комплексного числа z.
Найдем все необходимые значения для формулы:
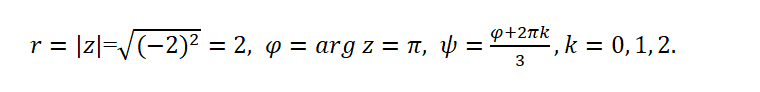
Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения:
Домашнее задание: Самостоятельно составить и решить уравнение с комплексными числами.
Условия: переменная z должна быть «спрятана» и представлена в качестве аргумента тригонометрической функции косинуса. Чтобы привести данное уравнение к привычной форме, нужно «вытащить» z, а для этого необходимо помнить, как решаются тригонометрические уравнения,а также знать, как применять свойства логарифмической функции от комплексного числа.
После того, как мы решили тригонометрическое уравнение с комплексным числом, получаем «голый» z, который представлен в качестве аргумента обратной тригонометрической функции. Чтобы преобразовать данное выражение, нужно использовать формулу разложения арккосинуса в логарифм.
Вместо z — выражение (3i/4) и дальше все делаем по приведенной выше формуле, преобразовывая выражение под корнем, используя свойства мнимой единицы i.
Как быть далее? Теперь будем использовать формулу для решения выражения с натуральным логарифмом.
Для того чтобы найти корни логарифмического уравнения, нужно найти модуль комплексного числа |z| и его аргумент φ = arg z. По сути, перед нами чисто мнимое число.
Теперь предлагаем ознакомиться с формулами, которые могут пригодиться при решении уравнений или неравенств с комплексными числами. Это формулы, где комплексное число выступает в роли аргумента тригонометрической функции, логарифмической функции или показательной функции.
Комплексные числа
 Алгебраическая форма записи комплексных чисел Алгебраическая форма записи комплексных чисел |
 Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме |
 Комплексно сопряженные числа Комплексно сопряженные числа |
 Модуль комплексного числа Модуль комплексного числа |
 Деление комплексных чисел, записанных в алгебраической форме Деление комплексных чисел, записанных в алгебраической форме |
 Изображение комплексных чисел радиус-векторами на координатной плоскости Изображение комплексных чисел радиус-векторами на координатной плоскости |
 Аргумент комплексного числа Аргумент комплексного числа |
 Тригонометрическая форма записи комплексного числа Тригонометрическая форма записи комплексного числа |
 Формула Эйлера. Экспоненциальная форма записи комплексного числа Формула Эйлера. Экспоненциальная форма записи комплексного числа |
 Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме |
 Извлечение корня натуральной степени из комплексного числа Извлечение корня натуральной степени из комплексного числа |
Алгебраическая форма записи комплексных чисел
Пусть x и y — произвольные вещественные числа.
Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.
Множество комплексных чисел является расширением множества вещественных чисел, поскольку множество вещественных чисел содержится в нём в виде пар (x, 0) .
Комплексные числа, заданные парами (0, y) , называют чисто мнимыми числами .
Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи .
Алгебраическая форма — это такая форма записи комплексных чисел, при которой комплексное число z, заданное парой вещественных чисел (x, y) , записывается в виде
| z = x + i y . | (1) |
где использован символ i , называемый мнимой единицей .
Число x называют вещественной (реальной) частью комплексного числа z = x + i y и обозначают Re z .
Число y называют мнимой частью комплексного числа z = x + i y и обозначают Im z .
Комплексные числа, у которых Im z = 0 , являются вещественными числами .
Комплексные числа, у которых Re z = 0 , являются чисто мнимыми числами .
Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.
Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
Умножение комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 , так же, как и операции сложения и вычитания, осуществляется по правилам умножения двучленов (многочленов), однако при этом учитывается важнейшее равенство, имеющее вид:
| i 2 = – 1 . | (2) |
По этой причине
Комплексно сопряженные числа
Два комплексных числа z = x + iy и 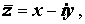
Операция перехода от комплексного числа к комплексно сопряженному с ним числу называется операцией комплексного сопряжения , обозначается горизонтальной чертой над комплексным числом и удовлетворяет следующим свойствам:
 | 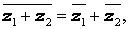 |
 | 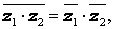 |
 | 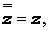 |
 | 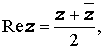 |
 | 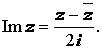 |
Модуль комплексного числа
Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле
Для произвольного комплексного числа z справедливо равенство:
а для произвольных комплексных чисел z1 и z2 справедливы неравенства:
 | 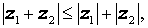 |
 | 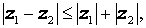 |
 | 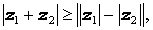 |
 | 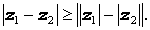 |
Замечание . Если z — вещественное число, то его модуль | z | равен его абсолютной величине.
Деление комплексных чисел, записанных в алгебраической форме
Деление комплексного числа z1 = x1 + i y1 на отличное от нуля комплексное число z2 = x2 + i y2 осуществляется по формуле
Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:
Деление на нуль запрещено.
Изображение комплексных чисел радиус-векторами координатной плоскости
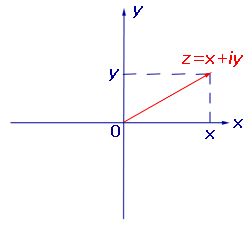
Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.
Назовем рассматриваемую плоскость комплексной плоскостью , и будем представлять комплексное число z = x + i y радиус–вектором с координатами (x , y).
Назовем ось абсцисс Ox вещественной осью , а ось ординат Oy – мнимой осью .
При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.
Аргумент комплексного числа
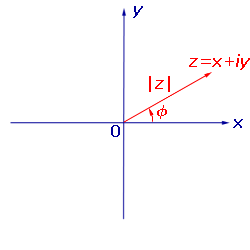
Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа z .
Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором z .
Аргумент комплексного числа z считают положительным, если поворот от положительного направления вещественной оси к радиус-вектору z происходит против часовой стрелки, и отрицательным — в случае поворота по часовой стрелке (см. рис.).
Считается, что комплексное число нуль аргумента не имеет.
Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где k — произвольное целое число, то вводится, главное значение аргумента , обозначаемое arg z и удовлетворяющее неравенствам:
Тогда оказывается справедливым равенство:
Если для комплексного числа z = x + i y нам известны его модуль r = | z | и его аргумент φ , то мы можем найти вещественную и мнимую части по формулам
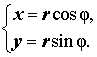 | (3) |
Если же комплексное число z = x + i y задано в алгебраической форме, т.е. нам известны числа x и y , то модуль этого числа, конечно же, определяется по формуле
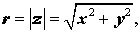 | (4) |
а аргумент определяется в соответствии со следующей Таблицей 1.
Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.
Таблица 1. – Формулы для определения аргумента числа z = x + i y
| Расположение числа z | Знаки x и y | Главное значение аргумента | Аргумент | Примеры |
| Положительная вещественная полуось | 0 | φ = 2kπ | 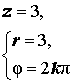 | |
| Первый квадрант | 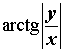 | 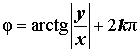 | 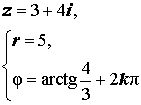 | |
| Положительная мнимая полуось | 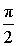 | 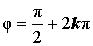 | 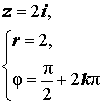 | |
| Второй квадрант | 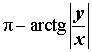 | 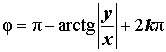 | 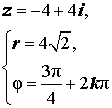 | |
| Отрицательная вещественная полуось | Положительная вещественная полуось | |||
| Знаки x и y | ||||
| Главное значение аргумента | 0 | |||
| Аргумент | φ = 2kπ | |||
| Примеры | 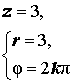 |
| Расположение числа z | Первый квадрант |
| Знаки x и y | |
| Главное значение аргумента | 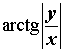 |
| Аргумент | 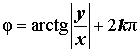 |
| Примеры | 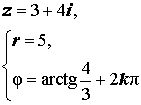 |
| Расположение числа z | Положительная мнимая полуось |
| Знаки x и y | |
| Главное значение аргумента | 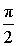 |
| Аргумент | 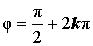 |
| Примеры | 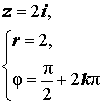 |
| Расположение числа z | Второй квадрант |
| Знаки x и y | |
| Главное значение аргумента | 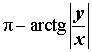 |
| Аргумент | 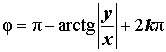 |
| Примеры | 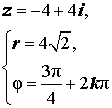 |
| Расположение числа z | Отрицательная вещественная полуось | ||||||||||
| Знаки x и y | Третий квадрант | ||||||||||
| Знаки x и y | Отрицательная мнимая полуось | ||||||||||
| Знаки x и y | Четвёртый квадрант | ||||||||||
| Знаки x и y | |||||||||||
| z = r (cos φ + i sin φ) , | (5) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (5) называют тригонометрической формой записи комплексного числа .
Формула Эйлера. Экспоненциальная форма записи комплексного числа
В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера :
| cos φ + i sin φ = e iφ . | (6) |
Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
| z = r e iφ , | (7) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (7) называют экспоненциальной (показательной) формой записи комплексного числа .
Из формулы (7) вытекают, в частности, следующие равенства:
а из формул (4) и (6) следует, что модуль комплексного числа
или, что то же самое, числа e iφ , при любом значении φ равен 1.
Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.
Действительно, умножение и деление двух произвольных комплексных чисел 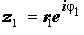
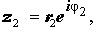
Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.
Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле
Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Извлечение корня натуральной степени из комплексного числа
Пусть 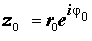
Корнем n — ой степени из числа z0 , где 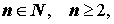
| z n = z0 . | (8) |
Для того, чтобы решить уравнение (8), перепишем его в виде
и заметим, что два комплексных числа, записанных в экспоненциальной форме, равны тогда и только тогда, когда их модули равны, а разность аргументов равна 2kπ , где k — произвольное целое число. По этой причине справедливы равенства
следствием которых являются равенства
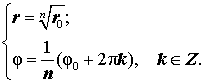 | (9) |
Из формул (9) вытекает, что уравнение (8) имеет n различных корней
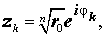 | (10) |
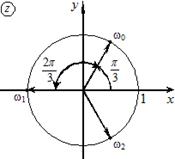
причем на комплексной плоскости концы радиус-векторов zk при k = 0 , . , n – 1 располагаются в вершинах правильного n — угольника, вписанного в окружность радиуса 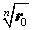
Замечание . В случае n = 2 уравнение (8) имеет два различных корня z1 и z2 , отличающихся знаком:
Пример 1 . Найти все корни уравнения
то по формуле (10) получаем:
Пример 2 . Решить уравнение
Решение . Поскольку дискриминант этого квадратного уравнения отрицателен, то вещественных корней оно не имеет. Для того, чтобы найти комплексные корни, выделим, как и в вещественном случае, полный квадрат:
http://matematyka.ru/reshenie-uravnenij-s-kompleksny-mi-chislami/
http://www.resolventa.ru/spr/algebra/complex.htm
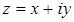 Комплексное число в алгебраической форме,(1)
Комплексное число в алгебраической форме,(1)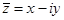 — комплексно сопряженное число числу z ;
— комплексно сопряженное число числу z ;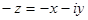 — противоположное число числу z ;
— противоположное число числу z ;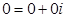 — комплексный ноль ;
— комплексный ноль ; – так обозначается множество комплексных чисел.
– так обозначается множество комплексных чисел.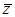 = 1 – i,
= 1 – i, 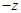 = –1 – i ;
= –1 – i ;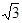 i Þ Re z = –1, Im z =
i Þ Re z = –1, Im z = 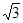 ,
, 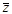 = –1 –
= –1 – 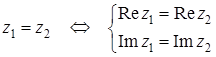 ;
;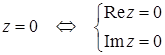 .
.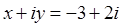
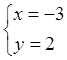 ;
;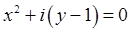
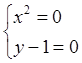
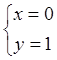 .
.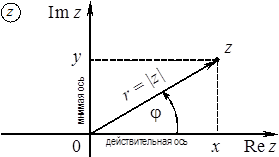
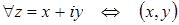
 Знак z во второй четверти означает, что система декартовых координат
Знак z во второй четверти означает, что система декартовых координат 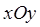 будет использоваться как комплексная плоскость.
будет использоваться как комплексная плоскость.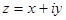 называется неотрицательное действительное число
называется неотрицательное действительное число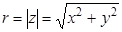 .(2)
.(2)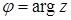 , причем
, причем 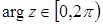 , или
, или 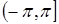 .
.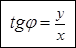 Аргумент комплексного числа ,(3)
Аргумент комплексного числа ,(3)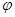 по его тангенсу обязательно нужно учитывать, в какой четверти на комплексной плоскости расположено число z :
по его тангенсу обязательно нужно учитывать, в какой четверти на комплексной плоскости расположено число z :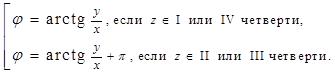
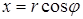 и
и 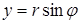 , то
, то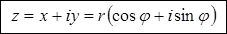 Тригонометрическая форма комплексного числа .(4)
Тригонометрическая форма комплексного числа .(4)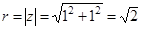 ,
,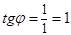 Þ
Þ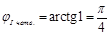
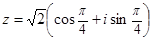 ;
;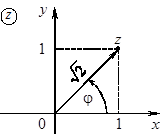
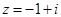 Þ
Þ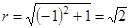 ,
,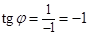 Þ
Þ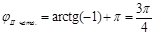
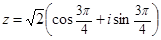 ;
;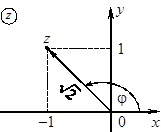
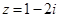 Þ
Þ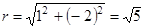 ,
,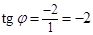 Þ
Þ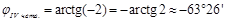 Þ
Þ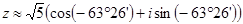 ;
;
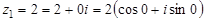 ,
,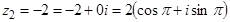 ;
;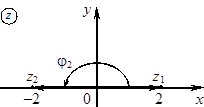
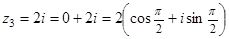 ,
,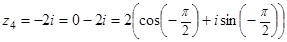 ;
;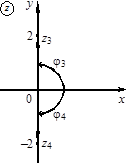
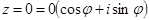 ,
, , j не определен.
, j не определен.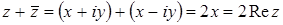 .
.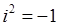 и приведением подобных по действительным и мнимым слагаемым.
и приведением подобных по действительным и мнимым слагаемым.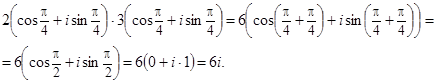
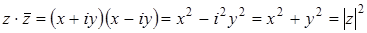 .
.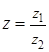 .
.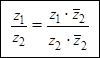 Деление комплексных чисел в алгебраической форме .(7)
Деление комплексных чисел в алгебраической форме .(7)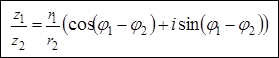 Деление комплексных чисел в тригонометрической форме .(8)
Деление комплексных чисел в тригонометрической форме .(8)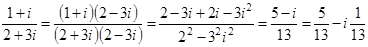 ;
;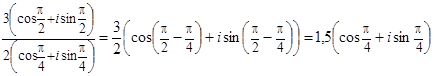 .
.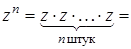
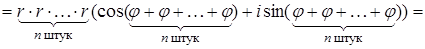
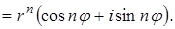
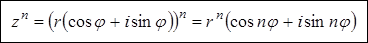 Формула Муавра,(9)
Формула Муавра,(9)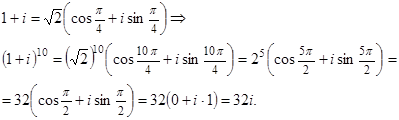
 или
или  сбрасыванием целого числа полных оборотов по свойствам периодичности функций
сбрасыванием целого числа полных оборотов по свойствам периодичности функций 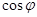 и
и 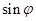 .
.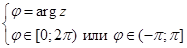 называют главным значением аргумента комплексного числа
называют главным значением аргумента комплексного числа 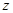 ;
;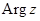 ;
;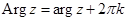 ,
, 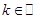 .
.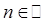 N, называется комплексное число w , такое что w n = z
N, называется комплексное число w , такое что w n = z 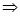
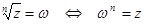 .
.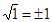 , так как
, так как 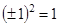 ;
;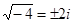 , так как
, так как 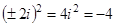 ;
;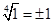 или
или 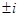 , так как
, так как 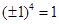 и
и  .
.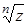 существует при «z и если z ¹ 0, то
существует при «z и если z ¹ 0, то 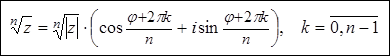 Извлечение корня натуральной степени из комплексного числа ,(10)
Извлечение корня натуральной степени из комплексного числа ,(10)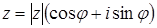 ,
,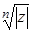 — арифметический корень на
— арифметический корень на 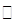 .
.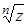 расположены регулярным образом на окружности радиусом
расположены регулярным образом на окружности радиусом 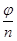 и углом регулярности
и углом регулярности 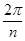 .
.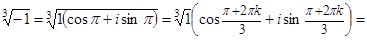
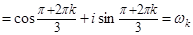 , k = 0, 1, 2 Þ
, k = 0, 1, 2 Þ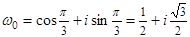 ,
,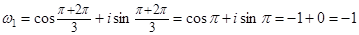 ,
, .
.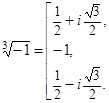
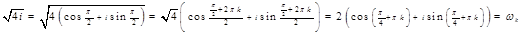 ,
, 
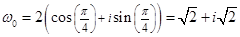
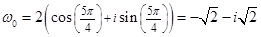 .
.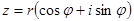 называется форма
называется форма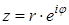 Показательная форма комплексного числа,(11)
Показательная форма комплексного числа,(11)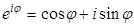 .
.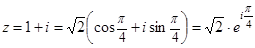 ;
;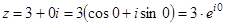 ;
;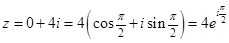 .
.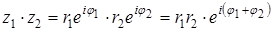 ,(12)
,(12)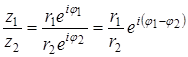 ,(13)
,(13)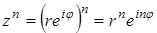 ,(14)
,(14)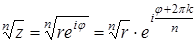 ,
, 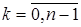 .(15)
.(15)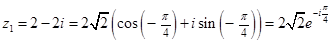 ,
,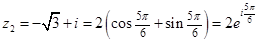 .
.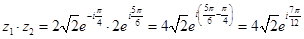 ;
;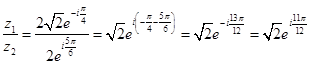 ;
;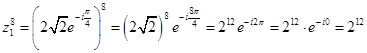 ;
;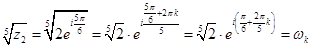 ,
, 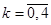
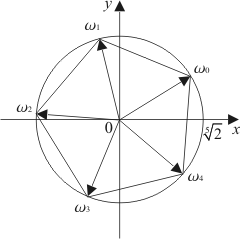
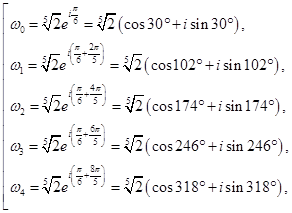
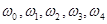 являются вершинами правильного пятиугольника, вписанного в окружность радиуса
являются вершинами правильного пятиугольника, вписанного в окружность радиуса 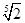 .
.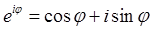 Þ
Þ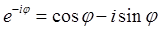 ,
,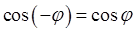 ,
, 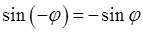 .
.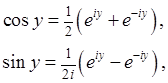 Формулы Эйлера(16)
Формулы Эйлера(16)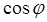 и
и 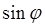 действительной переменной
действительной переменной 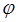 выражаются через показательную функцию (экспоненту) с чисто мнимым показателем.
выражаются через показательную функцию (экспоненту) с чисто мнимым показателем.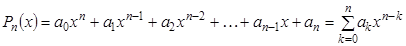 .(1)
.(1)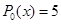 ;
;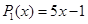 ;
;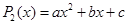 ,
, 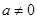 – квадратный трехчлен;
– квадратный трехчлен;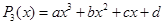 ,
, 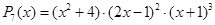 .
.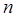 -й степени
-й степени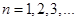 (2)
(2)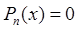 .
.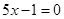 – алгебраическое уравнение первой степени,
– алгебраическое уравнение первой степени,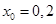 ;
;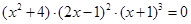 – алгебраическое уравнение седьмой степени,
– алгебраическое уравнение седьмой степени,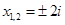 ,
, 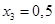 ,
, 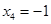 .
.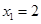 и
и 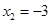 являются нулями функции
являются нулями функции 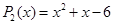 , так как
, так как 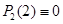 и
и 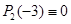 .
.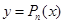 называются ее корнями. Например, числа
называются ее корнями. Например, числа 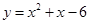 .
.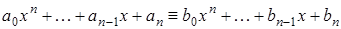 (3)
(3)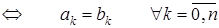 .
. (или «xÎ
(или «xÎ )
)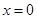 ; подставляя
; подставляя 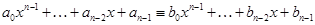 .(3’)
.(3’)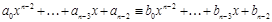 .
.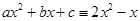 при
при 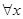
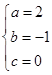 .
.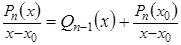 Теорема Безу,(4)
Теорема Безу,(4)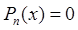 Þ
Þ 
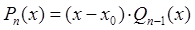 .(5)
.(5)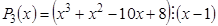 , так какP 3(1) º 0
, так какP 3(1) º 0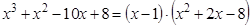 .
.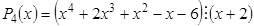 , так какP 4(–2) º 0
, так какP 4(–2) º 0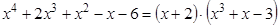 .
.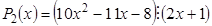 , так какP 2(–1/2) º 0
, так какP 2(–1/2) º 0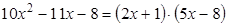 .
.