Решение алгебраических уравнений в simulink

Решение дифференциального уравнения различными методами, доступными SIMULINK

Страницы работы

Содержание работы

Файл Модели\САМРаботы02\САМ06а.doc 5 стр. 200 Кбайт

1. Решение дифференциального уравнения различными методами, доступными SIMULINK.

Пусть, к примеру, требуется решить линейное дифференциальное уравнение второго порядка с правой частью

. (П7.01)

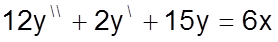
При использовании SIMULINK это уравнение можно решить несколькими способами.

Первый способ решения.

а) Разрабатывается блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Gain раздела Linear. Начнем с того, что разрешим его относительно второй производной

(П7.02)

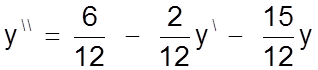
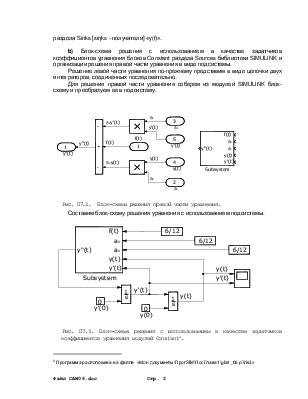
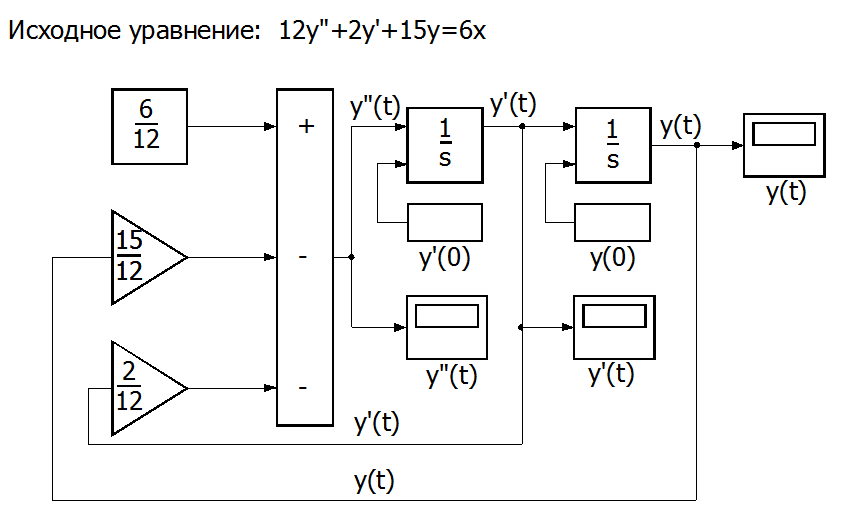
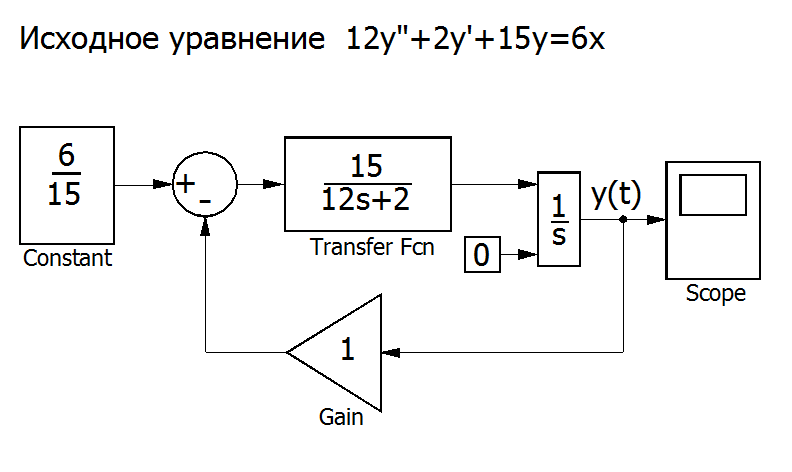
Полученное решение в модулях SIMULINK можно изобразить в виде

Рис. П7.1 Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Gain[1].

Для решения уравнения нами использованы 2 интегратора, 1 сумматор и 2 усилителя из раздела Linear библиотеки SIMULINK.

Вторая производная, согласно П7.02, должна получится путем вычитания из y₀ равного 6/12, производных, умноженных на соответствующие коэффициенты.

Вид и значение параметров решения можно наблюдать на экране блока Scope раздела Sinks [siŋks — получатели] «y(t)».

b) Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения блоков Constant раздела Sources библиотеки SIMULINK и организации решения правой части уравнения в виде подсистемы.

Решение левой части уравнения по-прежнему представим в виде цепочки двух интеграторов, соединенных последовательно.

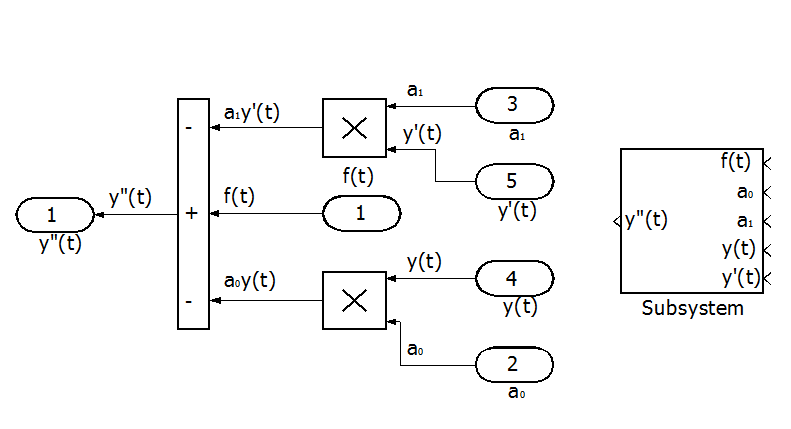
Для решения правой части уравнения соберем из модулей SIMULINK блок-схему и преобразуем ее в подсистему.

Рис. П7.2. Блок-схема решения правой части уравнения.

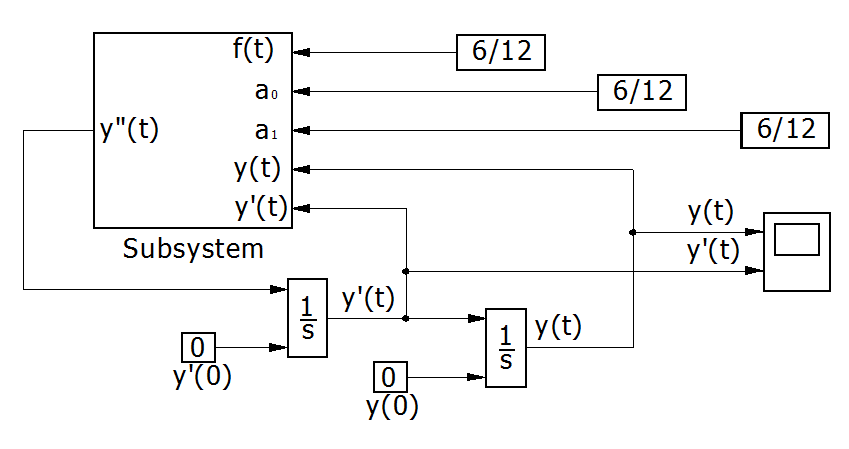
Составим блок-схему решения уравнения с использованием подсистемы.

Рис. П7.3. Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Constant[2].

Второй способ решения.

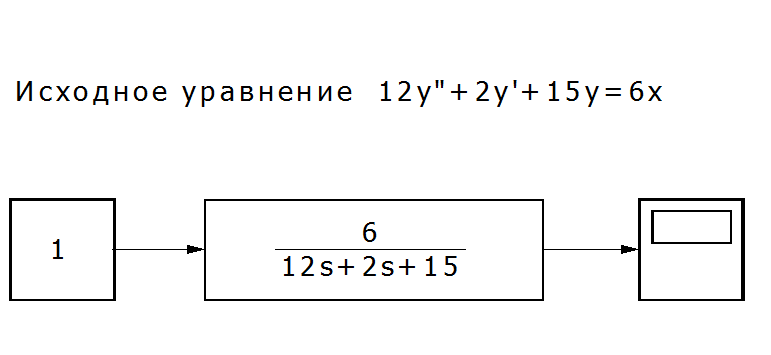
Используя SIMULINK, можно представить другой способ решения этого уравнения. Решение можно получить, используя модуль Transfer Fcn [‘trænsfə: Fkn] (Передаточное звено). В качестве входного сигнала будем использовать блок Constant раздела Sources [so:s — источники]

Рис. П7.4. Решение уравнения с использованием типовых структурных схем[3].

Вид и значение параметров решения можно наблюдать на экране блока Scope раздела Sinks [siŋks — получатели] «Интеграл».

Третий способ решения.

SIMULINK может предложить еще один способ решения данного дифференциального уравнения. Воспользовавшись методами структурных преобразований, данное уравнение можно представить в виде структурной схемы, состоящей из типовых модулей.

Рис. П7.5. Решение уравнения с использованием структурных преобразований[4].

Проведем исследование дифференциального уравнения 2 порядка

(П8.01)

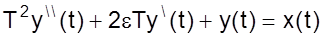
методами фазовой плоскости, используя возможности SIMULINK.

Начнем с того, что разрешим уравнение относительно старшей производной.

(П8.02)

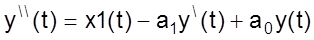
Решение левой части уравнения представим в виде цепочки из двух интеграторов соответственно настроенных.

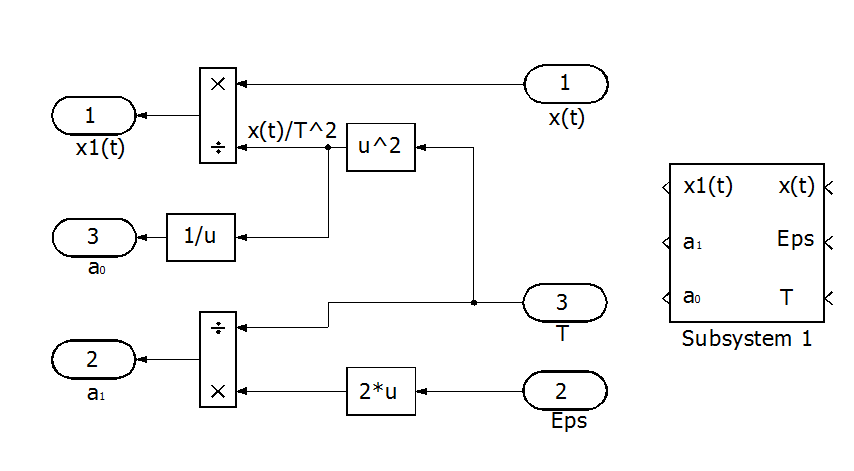
Для решения правой части уравнения создадим 2 подсистемы. Одну для формирования значений коэффициентов уравнения, разрешенного относительно старшей производной и вторую для решения собственно правой части уравнения.

Рис. П8.1 Блок-схема формирования коэффициентов уравнения.

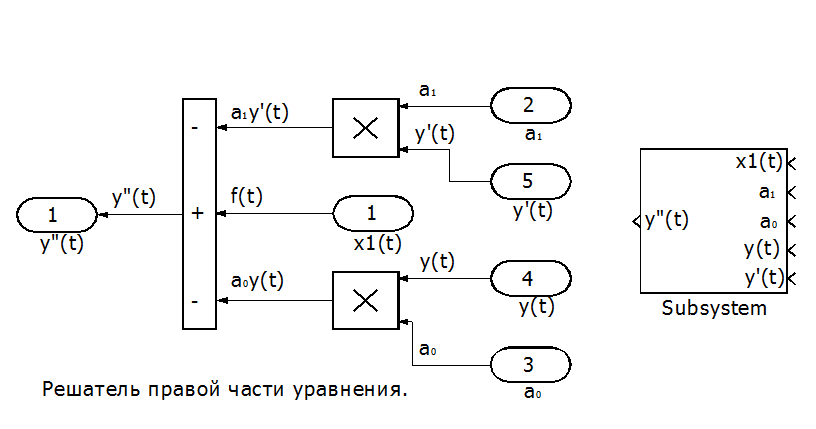
Рис. П8.2. Решатель правой части уравнения.

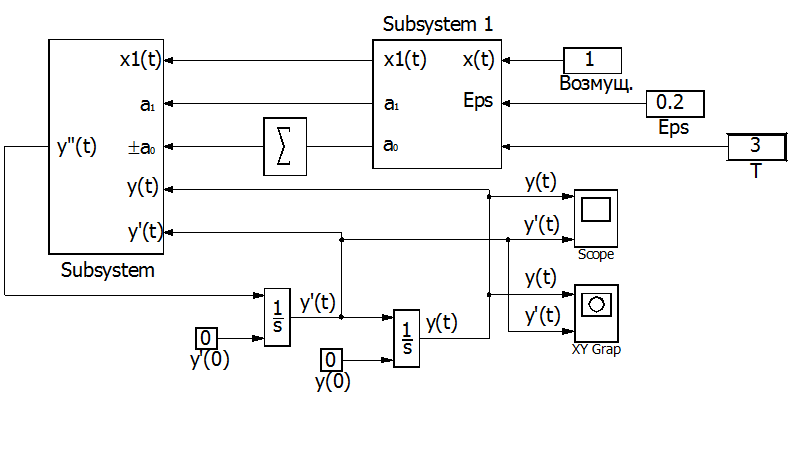
Решение дифференциального уравнения с учетом созданных подсистем будет иметь вид

Рис. П8.3. Блок-схема решения дифференциального уравнения[5].

Исследование фазового портрета.

Для наблюдения за фазовыми траекториями включим в качестве смотрового окна в блок-схему решения уравнения рис. П7.3 дополнительно модуль XY Graph из раздела Sinks библиотеки SIMULINK.

Сущность метода фазовой плоскости заключается в построении фазовых траекторий по дифференциальным уравнениям в системе координат: ось x — значение исследуемой величины u, ось y – скорость ее изменения du/dt. Процесс изменения траектории представляет собой движение изображающей точки на фазовой плоскости. Начальные условия определяют первоначальное положение изображающей точки на фазовой плоскости. Совокупность фазовых траекторий в плоскости (x, y) носит название фазовый портрет. Подробнее с методами фазовой плоскости можно ознакомиться по «Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем. Учебник для вузов. Изд. 4-е, перераб. и доп. М., «Машиностроение», 1978. Стр. 485-495».

Задачей нашего исследования является построение некоторых наиболее характерных фазовых портретов.

Рассмотрим следующие случаи характерные для уравнения 2 порядка:

[1] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris1»

[2] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris3»

[3] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris4»

[4] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris5»

[5] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p8ris3»

MATLAB — алгебра

До сих пор мы видели, что все примеры работают как в MATLAB, так и в его GNU, альтернативно называемом Octave. Но для решения основных алгебраических уравнений и MATLAB, и Octave немного отличаются, поэтому мы постараемся охватить MATLAB и Octave в отдельных разделах.

Мы также обсудим факторизацию и упрощение алгебраических выражений.

Решение основных алгебраических уравнений в MATLAB

Функция решения используется для решения алгебраических уравнений. В простейшем виде функция решения принимает в качестве аргумента уравнение, заключенное в кавычки.

Например, давайте решим для х в уравнении х-5 = 0

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

Вы также можете вызвать функцию решения как —

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

Вы можете даже не включать правую часть уравнения —

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

Если в уравнение входит несколько символов, то по умолчанию MATLAB предполагает, что вы решаете для x, однако функция решения имеет другую форму —

где вы также можете упомянуть переменную.

Например, давайте решим уравнение v — u — 3t 2 = 0, для v. В этом случае мы должны написать —

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

Решение основных алгебраических уравнений в октаве

Функция корней используется для решения алгебраических уравнений в Octave, и вы можете написать приведенные выше примеры следующим образом:

Например, давайте решим для х в уравнении х-5 = 0

Octave выполнит приведенный выше оператор и вернет следующий результат —

Вы также можете вызвать функцию решения как —

Octave выполнит приведенный выше оператор и вернет следующий результат —

Решение квадратичных уравнений в MATLAB

Функция решения также может решать уравнения более высокого порядка. Он часто используется для решения квадратных уравнений. Функция возвращает корни уравнения в массиве.

В следующем примере решается квадратное уравнение x 2 -7x +12 = 0. Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Решение квадратичных уравнений в октаве

В следующем примере решается квадратное уравнение x 2 -7x +12 = 0 в октаве. Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Решение уравнений высшего порядка в MATLAB

Функция решения также может решать уравнения более высокого порядка. Например, давайте решим кубическое уравнение как (x-3) 2 (x-7) = 0

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

В случае уравнений более высокого порядка корни длинные, содержащие много членов. Вы можете получить числовое значение таких корней, преобразовав их в двойные. В следующем примере решается уравнение четвертого порядка x 4 — 7x 3 + 3x 2 — 5x + 9 = 0.

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он возвращает следующий результат —

Обратите внимание, что последние два корня являются комплексными числами.

Решение уравнений высшего порядка в октаве

В следующем примере решается уравнение четвертого порядка x 4 — 7x 3 + 3x 2 — 5x + 9 = 0.

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он возвращает следующий результат —

Решение системы уравнений в MATLAB

Функция решения также может быть использована для генерации решений систем уравнений, включающих более одной переменной. Давайте рассмотрим простой пример, чтобы продемонстрировать это использование.

Давайте решим уравнения —

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Таким же образом вы можете решать большие линейные системы. Рассмотрим следующую систему уравнений —

Решающая система уравнений в октаве

У нас есть немного другой подход к решению системы ‘n’ линейных уравнений с ‘n’ неизвестными. Давайте рассмотрим простой пример, чтобы продемонстрировать это использование.

Давайте решим уравнения —

Такая система линейных уравнений может быть записана в виде единого матричного уравнения Ax = b, где A — матрица коэффициентов, b — вектор столбцов, содержащий правую часть линейных уравнений, а x — вектор столбцов, представляющий решение как показано в программе ниже —

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Таким же образом, вы можете решить большие линейные системы, как указано ниже —

Разложение и сбор уравнений в MATLAB

Функция расширения и сбора расширяет и собирает уравнение соответственно. Следующий пример демонстрирует понятия —

Когда вы работаете со многими символическими функциями, вы должны объявить, что ваши переменные являются символическими.

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Расширяя и собирая уравнения в октаве

Вам нужно иметь символьный пакет, который обеспечивает расширение и функцию сбора для расширения и сбора уравнения, соответственно. Следующий пример демонстрирует понятия —

Когда вы работаете со многими символическими функциями, вы должны объявить, что ваши переменные являются символическими, но у Octave другой подход к определению символических переменных. Обратите внимание на использование Sin и Cos , которые также определены в символической упаковке.

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Факторизация и упрощение алгебраических выражений

Факторная функция разлагает выражение, а функция упрощения упрощает выражение. Следующий пример демонстрирует концепцию —

пример

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Решение и моделирование линейного алгебраическое система уравнение в Matlab

РЕШЕНИЕ И МОДЕЛИРОВАНИЕ ЛИНЕЙНОГО АЛГЕБРАИЧЕСКОЕ СИСТЕМА УРАВНЕНИЕ В MATLAB

Ш. М. Туймуродов (преподаватель, Каршинский филиал ТУИТ)

(магистрантка, Каршинский филиал ТУИТ)

В моделировании разновидные объекты и процессы повстречаются в алгебраической, трансцендентной, линейной и других систем уравнений. Оценить правильность уравнений и решить их в моделировании играет большую роль. Построение уравнений определяются из их особенностей. У всех из таких способов есть свои особенности, чтобы решить их понадобится специальные знания. Увеличение неизвестных построенных моделей и с увеличением виды факторы усложняются их решение. По этому, в решении трудностей использование информационно-коммуникационных технологий облегчает работу и играет нужную роль в получении точного ответа.

Для решении разнотипных математических задач, создана система Matlab, при ней существуют его специальные функции. С помощью этих функций решаются задачи в частном виде.

Мы покажем решение системы линейно-алгебраических уравнений с помощью функций программы Matlab и моделировании в среде Simulink.

Дана система линейно-алгебраического уравнения:

Здесь а11, а22,…….,аnn – неизменяемые коэффициенты, х1, х2,……. хn — неизвестные, b1, b2,……. bn – свободные члены.

Нам требуется решить следующую систему линейно-алгебраического уравнения:

Через окно Command Window системы Matlab, вводим следующие коды, при этом найдется решение системы уравнения.

Для решения системы линейно-алгебраических уравнений (1) из система уравнений определяем следующие матрицы:

A*B=C, отсюда вычисляем неизвестные матрицы B, оно будет выглядеть следующим образом:

,

Здесь A-1 обратная матрица для матрицы A

Чтобы решить систему линейно-алгебраических уравнений в среде матриц, определяем элементы матрицы из системы уравнений и вводим их в окно команд программы Matlab:

>> C=[14;3] % матрица состоит из свободных членов

>> A1=inv(A) %A1 обратная матрица для матрицы

>> B=A1*C % B означает корень уравнения матрицы x1 и x2

Способ моделирования Matlab/Simulink

1-способ: При решении системы уравнений состоящие из неизменяемых чисел вводим каждый эквивалент дифференциальной величины . В среде Matlab/Simulink для произведения модели пишется следующий вид системы уравнений:

Загрузив программную систему Matlab и библиотечную панель Simulink Library Browser, выбераем пользовательский блок: Gain (умножение неизменяемого коэффициента в сигнал ), Constant (источник неизменяемого сигнала ), Integrator (интегральный сигнал), Display (произведение цифрового сигнала в виде числа) Scope (виртуальный оцилограф). В виртуальным осцилографе видно то, что графическая функция означает, что с истечением времени, продолжается часть неизменяемой системы уравнения. А в дисплеи системы уравнение цифрового решения отображается на экране в виде числа. Блок Simulink в составе Matlab для математических задач основан на разработке проектирования, сбора сложных устройств электроники и разработки их математических моделей.

Пользовательские блоки: Display, Constant, Gain, Sum, Integrator, Mux.

Рис 1. Построение моделей системы линейно-алгебраических уравнений и изображения графика в оциллографе

2-способ: Из панели библиотеки отделения Ports&Subsystems выбирается команда Subsystem и настраивается его составная структура, в зависимости от числа неизвестных чисел блоков Gain и увеличивается число блоков multiplexor в зависимости от числа уравнений. Входящие сигналы Multipleksora In1,In2,In3 в выходящие Out1 с раздела Math operations, вращающие на значения ноль вводится Algebraic Constraint. Вводим соответствующие коэффиценты в состав параметров в каждый блок Gain. После процесса моделирования нажимаем кнопку Run и в результате на экране можно увидеть ответ системы уравнений.

Рис 2. Настройка составного строения Мултиплексора

Пользовательские блоки: Subsystem, Display, Constant, Gain, Algebraic Constraint, Sum, Mux.

Рис 3. Схематический состав решения системы линейно — алгебраического уравнения с помощью модели мултиплексора

Таким образом, мы познакомились с системой Matlab и решения систем линейно-алгебраических уравнений помощью стандартных функций матрицы и способами моделирование Simulink. С помощью этих способов создаётся оптимизирование системы произведения, моделирование объектов и процесс оценивания правильности построения моделей и способы их решения. Нужно отметить, что курс «Высшая математика» из точных наук работает с матрицами, выполняет разные операции над ними и разрабатывает разные способы решения линейных уравнений. Особенно с помощью способа Matlab/Simulink моделирование линейных уравнений занимает важное место современной цифровой технике, в изучение телекоммуникационных технологий.

, , . Математическое и компьютерное моделирование процессов и систем в среде MATLAB/SIMULINK. Киев-2008, ст-18-22. Hally More. MATLAB for engineers. Prentice Hall 2012 y. Page.441 MATLAB. Учебное пособие. ГУИА. 2005. – 143 с. , . Методы решения математических задач в Maple. Белгород 2001 г. Ст-22. . Simulink 5/6/7. Самоучитель. ДМК издательство. Москва-2008 г.