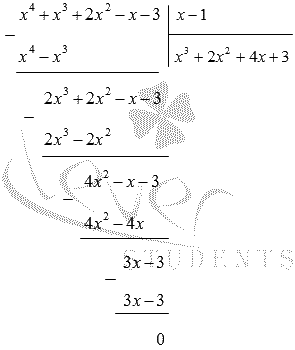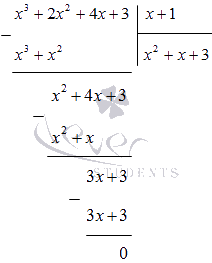Алгебраические уравнения высших степеней
Главная > Литература
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Алгебраические уравнения высших степеней
Составитель Волкова Н.О. Руководитель Будко Л.Ф.
МБОУ СОШ №1, х. Маяк. 2014г.
II Нестандартные способы решения квадратных уравнений…………………………………….4-8
III Решение уравнений высших степеней
3.1 Способы разложения на множители группировкой…..……………………………9-11
3.3. Метод неопределённых коэффициентов…………………………..…23-24
3.4.Введение новой переменной…………..25-29
3.4 Применение формул сокращённого умножения…………………………………..30-33
3.5 Применение теоремы Виета……………. 34
4.1Для самостоятельного решения………. 35-36
Каждый выпускник основной школы должен уметь решать алгебраические уравнения первой и второй степени, иначе, он не преодолеет порог в восемь баллов на ГИА по математике. В последнее время уравнения выше второй степени являются частью выпускных экзаменов за курс основной и средней школы, они встречаются на вступительных экзаменах в ВУЗы. Такие уравнения называются уравнениями высших степеней, изучение их выходит за рамки программы средней школы.
Материал данного сборника предназначен для самообразования учеников, которые любят математику и хотят знать больше.
В сборнике представлено 25 задач с решениями. Причём, решение каждого следующего задания отличается от предыдущего дополнительным «шагом» в решении, что заставляет , каждый раз, расширять теоретические знания по этой теме.
Этот материал можно использовать также для элективных занятий по математике в 9-11 классах.
Нестандартные способы решения квадратных уравнений
Общий вид квадратного уравнения — ах 2 + bx + c =0, где a ≠0, b , c –любые числа.
При решении квадратных уравнений можно использовать различные методы: разложение на множители, выделение полного квадрата, по формулам корней квадратного уравнения, по теореме Виета, графический способ, метод введения новой переменной (при решении биквадратных уравнений и уравнений, сводящихся к квадратным).
Решить уравнение (2х 2 -х-1)( 2х 2 -х-5)-5=0.
введём новую переменную t=2х 2 -х, тогда (t-1)( t-5)-5=0,
t 2 -6t=0, t(t-6)=0, t=0, t=6. Вернёмся к исходной переменной.
1. 2х 2 -х=0, х(2х-1)=0, х=0, х=

Ответ. х=0, х=

Метод коэффициентов для квадратных
Зависимость между коэффициентами или вид квадратного уравнения
х 1 =1, х 2 =
х 1 = -1, х 2 =
х 1 =-а, х 2 =
х 1 = а, х 2 =
х 1 =-а, х 2 =
ax 2 — (a 2 +1)x — a=0
х 1 = а, х 2 =
ах 2 +bx +c=0 → у 2 +by+ c∙a=0
х 1 =
1.Если a + b + c =0, то х 1 =1, х 2 =
Решить уравнение: 538х+841
Решение : введём новую переменную у =

. Если b = a + c ,то х 1 = -1, х 2 =
Решить уравнение: 1784х 2 + 583х -1201=0.
Решение: а=1784, b=583, c=-1201, b= a+c (1784+(-1201)=583),значит, х 1 =-1, х 2 =


.Если уравнение имеет вид ax 2 +( a 2 +1) x + a =0,то х 1 =-а, х 2 =
Решить уравнение 13x 2 +170x+13=0.
Решение: a=13, b= (13 2 +1)= 170 ,c=13. Выполняется зависимость между коэффициентами: b=a 2 +1, a=c. Используем формулы х 1 =-а, х 2 =
х =-13, х 2 =

4.В уравнении вида ax 2 — ( a 2 +1) x + a =0 х 1 = а, х 2 =
Решить уравнение 21x 2 — 442x+21=0.
Решение: a=21, b=- (21 2 +1)= 442,c=21. Выполняется зависимость между коэффициентами: b=-(a 2 +1), a=c. Используем формулы х 1 =а, х 2 =
х =21, х 2 =
Ответ: х =21, х 2 =
.В уравнении вида ax 2 +( a 2 +1) x — a =0 х 1 =-а, х 2 =
Решить уравнение 17x 2 +290x — 17=0.
Решение: a=17, b= (17 2 +1)= 290,c=-17. Выполняется зависимость между коэффициентами: b=a 2 +1, a= -c. Используем формулы х 1 =-а, х 2 =
х =-17, х 2 =
Ответ: х =-17, х 2 =
6.Если уравнение имеет вид ax 2 — ( a 2 +1) x — a =0,то х 1 = а, х 2 =
Решить уравнение 34x 2 — 1156x — 34=0.
Решение: a=34 , b= -(34 2 +1)= 1156 ,c=-34. Выполняется зависимость между коэффициентами: b=-(a 2 +1), a= -c. Используем формулы х 1 =а, х 2 =


7. Приём «переброски» старшего коэффициента
Решить уравнение 7х 2 -12х+ 5=0.
Решение: «перебросим» старший коэффициент и получим уравнение
у 2 -12у+35=0, по т. Виета у 1 =5, у 2 =7. Воспользуемся формулами х 1 =


Ответ: х 1 =
Решение уравнений высших степеней
3.1 Способы разложения на множители группировкой.
1. Неполные кубические уравнения.
а). d =0, с=0, b =0, ах 3 =0, x =0.
б). d =0, с=0, ах 3 + bx 2 =0, x 2 (ах+ b )=0, x =0, ax + b =0, x = 
в). d =0, ах 3 + bx 2 + cx =0, x (ах 2 + bx + c )=0, x =0, ах 2 + bx + c =0, х 1,2 =
г). d =0, b =0, ах 3 + cx =0, x (ах 2 + c )=0, x =0, ах 2 + c =0, x 2 = 


д). b =0, ах 3 + cx + d =0,
e ).с=0, ах 3 + bx 2 + d =0.
При решении выше перечисленных видов уравнений многочлен в левой части можно разложить на множители. В уравнениях 1(а-г)─ путём вынесения общего множителя за скобки. В уравнениях 1(д,е) и 2 – это группировка, и, в конечном итоге, вынесение общего множителя.
Решить уравнение вида 1(д) -х 3 +16х-15=0.
2. х(х+1)+15=0, х 2 +х+15=0, D=61, х 1,2 =
Ответ. х=1, х 1,2 =
Решить уравнение вида 1(е) 2х 3 +х 2 -3=0.
Преобразуем левую часть:
3х 3 -х 3 +х 2 -3=0, (3х 3 -3)+(- х 3 +х 2 )=0,
3(х 3 -1)-х 2 ( х-1)=0, 3(х-1)(х 2 +х+1)- х 2 ( х-1)=0,
(х-1)(3(х 2 +х+1)- х 2 )=0,
х-1=0, 3х 2 +3х+3- х 2 =0, 2х 2 +3х+3=0, D =-15, действительных корней нет.
2.Полные кубические уравнения.
ах 3 + bx 2 + cx + d =0, а≠0
Решить уравнение -6х 3 -х 2 +5х+2=0
Преобразуем левую часть: (-6х 3 -3х 2 ) +3х 2 -х 2 +5х+2=0, -3х 2 (2х+1) +(2х 2 +х) +(4х+2)=0, -3х 2 (2х+1) + х(2х+1) + 2(2х+1)=0, (2х+1)( -3х 2 +х+2)=0,
2х+1=0, х=-



Решить уравнение вида ах 3 +bх 2 +bх+а=0. Такие уравнения называют возвратными. Они обладают своеобразной «симметрией»: коэффициент при х 3 равен свободному члену, коэффициент при х 2 равен коэффициенту при х. Возвратные уравнения также решаются с помощью разложения на множители.[3]
Решение: 4х 3 -6х 2 -6х+4=0, 4(х 3 +1)-
6(х 2 +х)=0, 4(х+1)(х 2 -х+1)-6х(х+1)=0,
(х+1)(4х 2 -4х+4-6х)=0, (х+1)( 4х 2 -10х+4)=0, х+1 =0, 4х 2 -10х+4=0,
х=-1, х=2,х=

3.2 Cпособ разложения на множители очень эффективный, но при видимой простоте группировки очень не просто выбрать слагаемые для ее проведения. Универсальных способов нет, так что приходится каждый раз экспериментировать.
Теорема Безу. Остаток от деления многочлена Р n (х) на двучлен х-а равен значению этого многочлена при х=а, т.е. Р(а)= R .
Следствие1. Если х=а ─корень уравнения Р n (х)=0, то R =0 и многочлен Р n (х) делится на двучлен х-а.
Следствие 2. Если многочлен Р n (х) делится на двучлен х-а, то
х=а ─ корень уравнения Р n (х)=0. [3]
Другой способ разложения левой части уравнения ах 3 +bx 2 +cx+d=0, а≠0 на множители – применить теорему Безу и следствия из этой теоремы.
Чтобы использовать теорему Безу и следствия, необходимо изучить тему: «Деление многочленов нацело» и научиться делить многочлены «уголком».
Разделить многочлен 

Деление можно выполнять уголком.
Остаток равен 0, поэтому многочлен 

Выполнить деление многочленов:
Процесс деления продолжается до тех пор, пока остаток не будет равен нулю или степень очередного остатка не окажется меньше степени делителя.
Процесс подбора корня облегчает теорема.
а 0 х n + a 1 x n -1 + a 2 x n -2 . + a n -2 x + a n =0 c целыми коэффициентами а 0 , a 1 , a 2 , . a n -2 , a n ,где а 0≠ 0, имеет целые корни, то этот корень является делителем числа a n (свободного члена). [3]
Лекция по теме «Уравнения высших степеней. Методы их решения». 9-й класс
Разделы: Математика
Класс: 9
- Закрепить понятие целого рационального уравнения -й степени.
- Сформулировать основные методы решения уравнений высших степеней (n > 3).
- Обучить основным методам решения уравнений высших степеней.
- Научить по виду уравнения определять наиболее эффективный способ его решения.
Формы, методы и педагогические приемы, которые используются учителем на уроке:
- Лекционно-семинарская система обучения (лекции – объяснение нового материала, семинары – решение задач).
- Информационно-коммуникационные технологии (фронтальный опрос, устная работа с классом).
- Дифференцированное обучение, групповые и индивидуальные формы.
- Использование исследовательского метода в обучении, направленного на развитие математического аппарата и мыслительных способностей каждого конкретного ученика.
- Печатный материал – индивидуальный краткий конспект урока (основные понятия, формулы, утверждения, материал лекций сжато в виде схем или таблиц).
- Организационный момент.
Цель этапа: включить учащихся в учебную деятельность, определить содержательные рамки урока. - Актуализация знаний учащихся.
Цель этапа: актуализировать знания учащихся по изученным ранее смежным темам - Изучение новой темы (лекция). Цель этапа: сформулировать основные методы решения уравнений высших степеней (n > 3)
- Подведение итогов.
Цель этапа: еще раз выделить ключевые моменты в материале, изученном на уроке. - Домашнее задание.
Цель этапа: сформулировать домашнее задание для учащихся.
1. Организационный момент.
Формулировка темы урока: “Уравнения высших степеней. Методы их решения”.
2. Актуализация знаний учащихся.
Теоретический опрос – беседа. Повторение некоторых ранее изученных сведений из теории. Учащиеся формулируют основные определения и дают формулировки необходимых теорем. Приводят примеры, демонстрируя уровень полученных ранее знаний.
- Понятие уравнения с одной переменной.
- Понятие корня уравнения, решения уравнения.
- Понятие линейного уравнения с одной переменной, понятие квадратного уравнения с одной переменной.
- Понятие равносильности уравнений, уравнения-следствия (понятие посторонних корней), переход не по следствию (случай потери корней).
- Понятие целого рационального выражения с одной переменной.
- Понятие целого рационального уравнения n-й степени. Стандартный вид целого рационального уравнения. Приведенное целое рациональное уравнение.
- Переход к совокупности уравнений более низких степеней путем разложения исходного уравнения на множители.
- Понятие многочлена n-й степени от x. Теорема Безу. Следствия из теоремы Безу. Теоремы о корнях (Z-корни и Q-корни) целого рационального уравнения с целыми коэффициентами (соответственно приведенного и неприведенного).
- Схема Горнера.
3. Изучение новой темы.
Будем рассматривать целое рациональное уравнение n-й степени стандартного вида с одной неизвестной переменной x : Pn(x) = 0 , где Pn(x) = anx n + an-1x n-1 + a1x + a0 – многочлен n-й степени от x, an ≠ 0 . Если an = 1 то такое уравнение называют приведенным целым рациональным уравнением n-й степени. Рассмотрим такие уравнения при различных значениях n и перечислим основные методы их решения.
n = 1 – линейное уравнение.
n = 2 – квадратное уравнение. Формула дискриминанта. Формула для вычисления корней. Теорема Виета. Выделение полного квадрата.
n = 3 – кубическое уравнение.
Пример: x 3 – 4x 2 – x + 4 = 0 

Возвратное кубическое уравнение вида ax 3 + bx 2 + bx + a = 0. Решаем, объединяя члены с одинаковыми коэффициентами.
Пример: x 3 – 5x 2 – 5x + 1 = 0 



Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. При применении этого метода необходимо сделать акцент на том, что перебор в данном случае конечный, и корни мы подбираем по определенному алгоритму в соответствии с теоремой о Z-корнях приведенного целого рационального уравнения с целыми коэффициентами.
Пример: x 3 – 9x 2 + 23x – 15 = 0. Уравнение приведенное. Выпишем делители свободного члена <+1; +3; +5; +15>. Применим схему Горнера:
| x 3 | x 2 | x 1 | x 0 | вывод | |
| 1 | -9 | 23 | -15 | ||
| 1 | 1 | 1 х 1 – 9 = -8 | 1 х (-8) + 23 = 15 | 1 х 15 – 15 = 0 | 1 – корень |
| x 2 | x 1 | x 0 |
Получаем 

Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. При применении этого метода необходимо сделать акцент на том, что перебор в данном случае конечный и корни мы подбираем по определенному алгоритму в соответствии с теоремой о Q-корнях неприведенного целого рационального уравнения с целыми коэффициентами.
Пример: 9x 3 + 27x 2 – x – 3 = 0. Уравнение неприведенное. Выпишем делители свободного члена <+1; +3>. Выпишем делители коэффициента при старшей степени неизвестного. <+1; +3; +9> Следовательно, корни будем искать среди значений <+1; +

| x 3 | x 2 | x 1 | x 0 | вывод | |
| 9 | 27 | -1 | -3 | ||
| 1 | 9 | 1 x 9 + 27 = 36 | 1 x 36 – 1 = 35 | 1 x 35 – 3 = 32 ≠ 0 | 1 – не корень |
| -1 | 9 | -1 x 9 + 27 = 18 | -1 x 18 – 1 = -19 | -1 x (-19) – 3 = 16 ≠ 0 | -1 – не корень |
 | 9 |  x 9 + 27 = 30 x 9 + 27 = 30 |  x 30 – 1 = 9 x 30 – 1 = 9 |  x 9 – 3 = 0 x 9 – 3 = 0 | корень |
| x 2 | x 1 | x 0 |
Получаем 




Для удобства подсчета при подборе Q-корней бывает удобно сделать замену переменной, перейти к приведенному уравнению и подбирать Z-корни.
- Если можно воспользоваться заменой вида y = kx.
Формула Кардано. Существует универсальный метод решения кубических уравнений – это формула Кардано. Эту формулу связывают с именами итальянских математиков Джероламо Кардано (1501–1576), Николо Тарталья (1500–1557), Сципиона дель Ферро (1465–1526). Эта формула лежит за рамками нашего курса.
n = 4 – уравнение четвертой степени.
Пример: x 4 + 2x 3 + 5x 2 + 4x – 12 = 0 



Метод замены переменной.
- Возвратное уравнение четвертой степени вида ax 4 + bx 3 + cx 2 + bx + a = 0.
Решаем, объединяя члены с одинаковыми коэффициентами, путем замены вида
- Обобщенное возвратное уравнение четвертой степени вида ax 4 + bx 3 + cx 2 – bx + a = 0.
- Обобщенное возвратное уравнение четвертой степени вида ax 4 + bx 3 + cx 2 + kbx + k 2 a = 0.
- Замена общего вида. Некоторые стандартные замены.
Пример 3. Замена общего вида (вытекает из вида конкретного уравнения).
Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Формула общего вида. Существует универсальный метод решения уравнений четвертой степени. Эту формулу связывают с именем Людовико Феррари (1522–1565). Эта формула лежит за рамками нашего курса.
n > 5 – уравнения пятой и более высоких степеней.
Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Симметрические уравнения. Любое возвратное уравнение нечетной степени имеет корень x = -1 и после разложения его на множители получаем, что один сомножитель имеет вид (x + 1), а второй сомножитель – возвратное уравнение четной степени (его степень на единицу меньше, чем степень исходного уравнения). Любое возвратное уравнение четной степени вместе с корнем вида x = φ содержит и корень вида 
Метод замены переменной. Использование однородности.
Не существует формулы общего вида для решения целых уравнений пятой степени (это показали итальянский математик Паоло Руффини (1765–1822) и норвежский математик Нильс Хенрик Абель (1802–1829)) и более высоких степеней (это показал французский математик Эварист Галуа (1811–1832)).
- Напомним еще раз, что на практике возможно использование комбинации перечисленных выше методов. Удобно переходить к совокупности уравнений более низких степеней путем разложения исходного уравнения на множители.
- За рамками нашего сегодняшнего обсуждения остались широко используемые на практике графические методы решения уравнений и методы приближенного решения уравнений высших степеней.
- Бывают ситуации, когда у уравнения нет R-корней. Тогда решение сводится к тому, чтобы показать, что уравнение корней не имеет. Для доказательства анализируем поведение рассматриваемых функций на промежутках монотонности. Пример: уравнение x 8 – x 3 + 1 = 0 не имеет корней.
- Использование свойства монотонности функций. Бывают ситуации, когда использование различных свойств функций позволяет упростить поставленную задачу.
Пример 1: уравнение x 5 + 3x – 4 = 0 имеет один корень x = 1. По свойству монотонности анализируемых функций других корней нет.
Пример 2: уравнение x 4 + (x – 1) 4 = 97 имеет корни x1 = -2 и x2 = 3. Проанализировав поведение соответствующих функций на промежутках монотонности, заключаем, что других корней нет.
4. Подведение итогов.
Резюме: Теперь мы овладели основными методами решения различных уравнений высших степеней (для n > 3). Наша задача научиться эффективно использовать перечисленные выше алгоритмы. В зависимости от вида уравнения мы должны будем научиться определять, какой способ решения в данном случае является наиболее эффективным, а также правильно применять выбранный метод.
5. Домашнее задание.
[1]: п.7, стр. 164–174, №№ 33–36, 39–44, 46,47.
[4]: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.
Возможные темы докладов или рефератов по данной тематике:
- Формула Кардано
- Графический метод решения уравнений. Примеры решения.
- Методы приближенного решения уравнений.
Анализ усвоения материала и интереса учащихся к теме:
Опыт показывает, что интерес учащихся в первую очередь вызывает возможность подбора Z-корней и Q-корней уравнений при помощи достаточно простого алгоритма с использованием схемы Горнера. Также учащиеся интересуются различными стандартными типами замены переменных, которые позволяют существенно упрощать вид задачи. Особый интерес обычно вызывают графические методы решения. В этом случае дополнительно можно разобрать задачи на графический метод решения уравнений; обсудить общий вид графика для многочлена 3, 4, 5 степени; проанализировать, как связано число корней уравнений 3, 4, 5 степени с видом соответствующего графика. Ниже приведен список книг, в которых можно найти дополнительную информацию по данной тематике.
- Виленкин Н.Я. и др. “Алгебра. Учебник для учащихся 9 классов с углубленным изучением математики” – М., Просвещение, 2007 – 367 с.
- Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. “За страницами учебника математики. Арифметика. Алгебра. 10-11 класс” – М., Просвещение, 2008 – 192 с.
- Выгодский М.Я. “Справочник по математике” – М., АСТ, 2010 – 1055 с.
- Галицкий М.Л. “Сборник задач по алгебре. Учебное пособие для 8-9 классов с углубленным изучением математики” – М., Просвещение, 2008 – 301 с.
- Звавич Л.И. и др. “Алгебра и начала анализа. 8–11 кл. Пособие для школ и классов с углубленным изучением математики” – М., Дрофа, 1999 – 352 с.
- Звавич Л.И., Аверьянов Д.И., Пигарев Б.П., Трушанина Т.Н. “Задания по математике для подготовки к письменному экзамену в 9 классе” – М., Просвещение, 2007 – 112 с.
- Иванов А.А., Иванов А.П. “Тематические тесты для систематизации знаний по математике” ч.1 – М., Физматкнига, 2006 – 176 с.
- Иванов А.А., Иванов А.П. “Тематические тесты для систематизации знаний по математике” ч.2 – М., Физматкнига, 2006 – 176 с.
- Иванов А.П. “Тесты и контрольные работы по математике. Учебное пособие”. – М., Физматкнига, 2008 – 304 с.
- Лейбсон К.Л. “Сборник практических заданий по математике. Часть 2–9 класс” – М., МЦНМО, 2009 – 184 с.
- Макарычев Ю.Н., Миндюк Н.Г. “Алгебра. Дополнительные главы к школьному учебнику 9 класса. Учебное пособие для учащихся школ и классов с углубленным изучением математики.” – М., Просвещение, 2006 – 224 с.
- Мордкович А.Г. “Алгебра. Углубленное изучение. 8 класс. Учебник” – М., Мнемозина, 2006 – 296 с.
- Савин А.П. “Энциклопедический словарь юного математика” – М., Педагогика, 1985 – 352 с.
- Сурвилло Г.С., Симонов А.С. “Дидактические материалы по алгебре для 9 класса с углубленным изучением математики” – М., Просвещение, 2006 – 95 с.
- Чулков П.В. “Уравнения и неравенства в школьном курсе математик. Лекции 1–4” – М., Первое сентября, 2006 – 88 с.
- Чулков П.В. “Уравнения и неравенства в школьном курсе математик. Лекции 5–8” – М., Первое сентября, 2009 – 84 с.
Решение уравнений высших степеней
В общем случае уравнение, имеющее степень выше 4 , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4 -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.
Уравнения высшей степени с целыми коэффициентами
Все уравнения, имеющие вид a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 , мы можем привести к уравнению той же степени с помощью умножения обеих частей на a n n — 1 и осуществив замену переменной вида y = a n x :
a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n — 1 · a n n — 1 · x n — 1 + … + a 1 · ( a n ) n — 1 · x + a 0 · ( a n ) n — 1 = 0 y = a n x ⇒ y n + b n — 1 y n — 1 + … + b 1 y + b 0 = 0
Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид x n + a n x n — 1 + … + a 1 x + a 0 = 0 .
Схема решения уравнения
Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a 0 . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x — x 1 · P n — 1 ( x ) = 0 . Здесь x 1 является корнем уравнения, а P n — 1 ( x ) представляет собой частное от деления x n + a n x n — 1 + … + a 1 x + a 0 на x — x 1 .
Подставляем остальные выписанные делители в P n — 1 ( x ) = 0 , начав с x 1 , поскольку корни могут повторяться. После получения тождества корень x 2 считается найденным, а уравнение может быть записано в виде ( x — x 1 ) ( x — x 2 ) · P n — 2 ( x ) = 0 .Здесь P n — 2 ( x ) будет частным от деления P n — 1 ( x ) на x — x 2 .
Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m . После этого исходное уравнение можно представить как x — x 1 x — x 2 · … · x — x m · P n — m ( x ) = 0 . Здесь P n — m ( x ) является многочленом n — m -ной степени. Для подсчета удобно использовать схему Горнера.
Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.
У нас в итоге получилось уравнение P n — m ( x ) = 0 , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.
Покажем на конкретном примере, как применяется такая схема решения.
Условие: найдите решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0 .
Решение
Начнем с нахождений целых корней.
У нас есть свободный член, равный минус трем. У него есть делители, равные 1 , — 1 , 3 и — 3 . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.
При x , равном единице, мы получим 1 4 + 1 3 + 2 · 1 2 — 1 — 3 = 0 , значит, единица будет корнем данного уравнения.
Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 — x — 3 на ( х — 1 ) в столбик:
Значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
Перебираем возможные делители дальше, но подставляем их в равенство x 3 + 2 x 2 + 4 x + 3 = 0 :
1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 ( — 1 ) 3 + 2 · ( — 1 ) 2 + 4 · — 1 + 3 = 0
У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный — 1 .
Делим многочлен x 3 + 2 x 2 + 4 x + 3 на ( х + 1 ) в столбик:
x 4 + x 3 + 2 x 2 — x — 3 = ( x — 1 ) ( x 3 + 2 x 2 + 4 x + 3 ) = = ( x — 1 ) ( x + 1 ) ( x 2 + x + 3 )
Подставляем очередной делитель в равенство x 2 + x + 3 = 0 , начиная с — 1 :
— 1 2 + ( — 1 ) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 ( — 3 ) 2 + ( — 3 ) + 3 = 9 ≠ 0
Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.
Оставшиеся корни будут корнями выражения x 2 + x + 3 .
D = 1 2 — 4 · 1 · 3 = — 11 0
Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x = — 1 2 ± i 11 2 .
Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.
| x i | коэффициенты многочлена | ||||
| 1 | 1 | 2 | — 1 | — 3 | |
| 1 | 1 | 1 + 1 · 1 = 2 | 2 + 2 · 1 = 4 | — 1 + 4 · 1 = 3 | — 3 + 3 · 1 = 0 |
В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
После нахождения следующего корня, равного — 1 , мы получаем следующее:
| x i | коэффициенты многочлена | |||
| 1 | 2 | 4 | 3 | |
| 1 | 1 | 2 + 1 · ( — 1 ) = 1 | 4 + 1 · ( — 1 ) = 3 | 3 + 3 · ( — 1 ) = 0 |
Далее мы приходим к разложению x — 1 x + 1 x 2 + x + 3 = 0 . Потом, проверив оставшиеся делители равенства x 2 + x + 3 = 0 , вычисляем оставшиеся корни.
Ответ: х = — 1 , х = 1 , x = — 1 2 ± i 11 2 .
Условие: решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0 .
Решение
У свободного члена есть делители 1 , — 1 , 2 , — 2 , 3 , — 3 , 4 , — 4 , 6 , — 6 , 12 , — 12 .
Проверяем их по порядку:
1 4 — 1 3 — 5 · 1 2 + 12 = 7 ≠ 0 ( — 1 ) 4 — ( — 1 ) 3 — 5 · ( — 1 ) 2 + 12 = 9 ≠ 0 2 4 · 2 3 — 5 · 2 2 + 12 = 0
Значит, x = 2 будет корнем уравнения. Разделим x 4 — x 3 — 5 x 2 + 12 на х — 2 , воспользовавшись схемой Горнера:
| x i | коэффициенты многочлена | ||||
| 1 | — 1 | — 5 | 0 | 12 | |
| 2 | 1 | — 1 + 1 · 2 = 1 | — 5 + 1 · 2 = — 3 | 0 — 3 · 2 = 3 | 12 — 6 · 2 = 0 |
В итоге мы получим x — 2 ( x 3 + x 2 — 3 x — 6 ) = 0 .
Проверяем делители дальше, но уже для равенства x 3 + x 2 — 3 x — 6 = 0 , начиная с двойки.
2 3 + 2 2 — 3 · 2 — 6 = 0
Значит, 2 опять будет корнем. Разделим x 3 + x 2 — 3 x — 6 = 0 на x — 2 :
| x i | коэффициенты многочлена | |||
| 1 | 1 | — 3 | — 6 | |
| 2 | 1 | 1 + 1 · 2 = 3 | — 3 + 3 · 2 = 3 | — 6 + 3 · 2 = 0 |
В итоге получим ( x — 2 ) 2 · ( x 2 + 3 x + 3 ) = 0 .
Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.
Решим квадратное уравнение:
x 2 + 3 x + 3 = 0 D = 3 2 — 4 · 1 · 3 = — 3 0
Получаем комплексно сопряженную пару корней: x = — 3 2 ± i 3 2 .
Ответ: x = — 3 2 ± i 3 2 .
Условие: найдите для уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0 действительные корни.
Решение
x 4 + 1 2 x 3 — 5 2 x — 3 = 0 2 x 4 + x 3 — 5 x — 6 = 0
Выполняем домножение 2 3 обеих частей уравнения:
2 x 4 + x 3 — 5 x — 6 = 0 2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0
Заменяем переменные y = 2 x :
2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0 y 4 + y 3 — 20 y — 48 = 0
В итоге у нас получилось стандартное уравнение 4 -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = — 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 .
Ответ: x 1 = — 1 , x 2 = 3 2
Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени.
http://urok.1sept.ru/articles/646258
http://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-vysshih-stepenej/