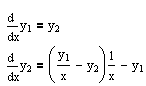Решение частных дифференциальных уравнений matlab

Решение ОДУ в Matlab

Доброго времени суток! Сегодня мы поговорим о решении ОДУ (обыкновенных дифференциальных уравнений) в Matlab. Перед тем как мы начнём обсуждать данную тему, советую вам ознакомиться с темой: Численное дифференцирование в Matlab, чтобы лучше понимать теоретическую составляющую решения ОДУ.

Обыкновенные дифференциальные уравнения

С помощью дифференциальных уравнений можно описать разные задачи: движения системы, взаимодействующих материальных точек, химической кинетики и т.д. Различают три типа задач для систем диф. уравнений:

• Задача Коши
• Краевая задача
• Задача на собственные значения

Кратко расскажу о их сути:

Задача Коши предполагает дополнительные условия в виде значения функции в определённой точке.
Краевая задача подразумевает поиск решения на заданном отрезке с краевыми (граничными) условиями в концах интервала или на границе области.
Задача на собственные значения — помимо искомых функций и их производных, в уравнение входят дополнительное несколько неизвестных параметров, которые являются собственными значениями.

Методы решения дифференциальных уравнений

Решение ОДУ в Matlab и не только, в первую очередь, сводится к выбору порядка численного метода решения. Порядок численного метода не связан с порядком дифференциального уравнения. Высокий порядок у численного метода означает его скорость сходимости.

В случае большого интервала, с помощью алгоритмов с низким порядком сжимают интервал с решениями и находят приблизительные корни, а затем уже уточняют корни с помощью методов с высоким порядком.

Решение обыкновенных дифференциальных уравнений в Matlab можно реализовать «своими ручками», прописав алгоритм по разным схемам. Но также в Matlab есть встроенные функции, выполняющие все стандартные задачи.

Метод Рунге-Кутта первого порядка

Методы Рунге-Кутта представляют собой разложения в ряд Тейлора и от количества использованных элементов ряда зависит порядок этого метода. Следовательно, помимо Рунге-Кутта первого порядка, вы сможете увидеть методы других порядков. Иногда их называют другими именами.

Например, Метод Рунге-Кутта первого порядка, также известен как Метод Эйлера или Метод ломаных. Информацию о его математическом и графическом представлении советую поискать в гугл. Мы же поговорим о том, как Метод Рунге-Кутта первого порядка реализуется в Matlab для решения ОДУ. Например:

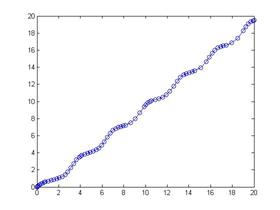
Решить и привести график ошибки уравнения y’ = y*x методом Рунге-Кутта первого порядка (Методом Эйлера, Методом ломаных).

Погрешность Метода Рунге-Кутта 1 порядка

» data-medium-file=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?fit=300%2C236&ssl=1″ data-large-file=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?fit=622%2C489&ssl=1″ loading=»lazy» src=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/%D0%A0%D1%83%D0%BD%D0%B3%D0%B5-1-%D0%BF%D0%BE%D0%B3%D1%80%D0%B5%D1%88%D0%BD%D0%BE%D1%81%D1%82%D1%8C.png?resize=622%2C489″ alt=»Погрешность метода 1 порядка» width=»622″ height=»489″ srcset=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?w=629&ssl=1 629w, https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?resize=300%2C236&ssl=1 300w» sizes=»(max-width: 622px) 100vw, 622px» data-recalc-dims=»1″ />
На данном графике показана зависимость величины ошибки от шага.

Метод Рунге-Кутта второго порядка

Также известен как Метод Эйлера-Коши. Как видите, во второй части уравнения происходит обращения к следующему шагу. Но как тогда быть, если нам ещё не известен следующий шаг? Всё просто. Метод Рунге-Кутта второго порядка — это всё тот же метод первого порядка, однако, на половине шага происходит нахождение «первичного» решения, а затем происходит его уточнение. Это позволяет поднять порядок скорости сходимости до двух.

Решить и привести график ошибки уравнения u’ = u*x методом Рунге-Кутта второго порядка.

По сравнению с Рунге-Куттом первого порядка изначальная ошибка уже гораздо меньше.

Мы не будем говорить о третьем порядке, потому что задачи на третий порядок встречаются редко, но если будет необходимо, пишите в комментариях, выложу.

Метод Рунге-Кутта четвёртого порядка

Метод Рунге-Кутта четвёртого порядка считается самым распространённым. Тем не менее, работает он аналогично второму и третьему порядку.

Решить и привести график ошибки уравнения u’ = u*x методом Рунге-Кутта четвёртого порядка.

Как видите, на последней картинке размерность ошибки на столько мала, что пришлось воспользоваться loglog() для лучшей видимости.

Решение ОДУ в Matlab стандартными средствами

Стоит отметить, что мы с вами разобрали только один самый известный метод решения ОДУ с разными порядками. Однако, методов очень много.

Для решения дифференциальных уравнений и систем в MATLAB предусмотрены следующие функции:

ode45 (f, interval, X0, [options])
ode23 (f, interval, X0, [options])
ode113 (f, interval, X0, [options])
ode15s (f, interval, X0, [options])
ode23s (f, interval, X0, [options])
ode23t (f, interval, X0, [options])
ode23tb (f, interval, X0, [options])

Входными параметрами этих функций являются:

• f — вектор-функция для вычисления правой части уравнения системы уравнений;
• interval — массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы;
• Х0 — вектор начальных условий системы дифференциальных уравнений;
• options — параметры управления ходом решения дифференциального уравнения или системы.

Все функции возвращают:

• массив Т — координаты узлов сетки, в которых ищется решение;
• матрицу X, i-й столбец которой является значением вектор-функции решения в узле Тi.

В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.

Для решения жёстких систем предназначены функция ode15s, в которой реализован метод Гира, и функция ode23s, реализующая метод Розенброка. Для получения более точного решения жёсткой системы лучше использовать функцию ode15s. Для решения системы с небольшим числом жёсткости можно использовать функцию ode23t, а для грубой оценки подобных систем служит функция ode23tb.

Символьное решение обыкновенных дифференциальных уравнений произвольного порядка осуществляет функция dsolve r = dsolve(‘eq1,eq2,…’, ‘cond1,cond2,…‘, ‘v’)
Пример использования:

На этом мы закончим. Если остались вопросы, задавайте их в комментариях. Также вы можете скачать исходники чтобы лучше понять тему: «Решение ОДУ в Matlab».

Решение частных дифференциальных уравнений matlab

Дифференциальные уравнения и системы уравнений

Для решения дифференциальных уравнений и систем в MATLAB предусмотрены следующие функции ode45(f, interval, X0 [, options]), ode23(f, interval, X0 [, options]), ode113(f, interval, X0 [, options]), odel5s(f, interval, X0 [, options]), ode23s(f, interval, X0 [, options]), ode23t (f, interval, X0 [,options]) и ode23tb(f, interval, X0 [, options]).

Входными параметрами этих функций являются:

• f — вектор-функция для вычисления правой части уравнения системы уравнений
• interval — массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы;
• Х0 — вектор начальных условий системы дифференциальных систем
• options — параметры управления ходом решения дифференциального уравнения или системы.

Все функции возвращают:

• массив Т — координаты узлов сетки, в которых ищется решение;
• матрицу X, i-й столбец которой является значением вектор-функции решения в узле Тi

В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.

В М-файле с именем pr 7. m пишем:

Потом в командном окне вызываем функцию ode113:

ode113(@pr7,[0 20],0) %Метод Адамса: @ pr 7 – ссылка на М-функцию, [0 20]- интервалы интегрирования,0 — условие: y(0)=0

Результатом будет график:

Необходимо реализовать метод Рунге-Кутта 4 порядка и решить задачу Коши для предложенной системы дифференциальных уравнений:

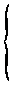
В М-файле с именем pr 8. m пишем:

Потом в командном окне вызываем функцию ode 45:

Решение частных дифференциальных уравнений matlab

Название работы: MATLAB. Численное решение дифференциальных уравнений

Категория: Лабораторная работа

Предметная область: Информатика, кибернетика и программирование

Описание: Математический пакет MATLAB упростит решение дифференциальных уравнений. Для решения обыкновенных дифференциальных уравнений (ODE) могут быть применены численные методы, которые в MATLAB реализованы в специальных функциях-решателях.

Дата добавления: 2015-01-11

Размер файла: 315.39 KB

Работу скачали: 537 чел.

Лабораторная работа №6

MATLAB. Численное решение дифференциальных уравнений.

Исходные данные: математический пакет MATLAB.

1. Генерация случайных чисел
2. Решение дифференциального уравнения с начальными условиями (первого и второго порядков)
3. Решение уравнений в частных производных

Генерация случайных чисел в MatLab осуществляет функция randn ( n , m )

% График нормального распределения

Решение обыкновенных дифференциальных уравнений

Для решения обыкновенных дифференциальных уравнений ( ODE ) могут быть применены численные методы, которые в MATLAB реализованы в специальных функциях-решателях: ode 45, ode 23, ode 113.

Функции ode 23 и ode 45 предназначены для численного интегрирования систем ОДУ. Они применимы как для решения простых дифференциальных уравнений, так и для моделирования сложных динамических систем.

Любая система нелинейных ОДУ может быть представлена как система дифференциальных уравнений 1-го порядка в явной форме Коши:

[ t , X ] = ode 23(‘ ‘, t 0, tf , x 0)

[t, X] = ode23(‘ ‘, t0, tf, x0, tol, trace)

[t, X] = ode45(‘ ‘, t0, tf, x0)

[t, X] = ode45(‘ ‘, t0, tf, x0, tol, trace)

где x — вектор состояния;

f — нелинейная вектор-функция от переменных x , t .

[ t , X ] = ode 23(‘ ‘, t 0, tf , x 0, tol , trace ) и

[ t , X ] = = ode 45(‘ ‘, t 0, tf , x 0, tol , trace ) интегрируют системы ОДУ, используя формулы Рунге — Кутта соответственно 2-го и 3-го или 4-го и 5-го порядка.

Эти функции имеют следующие параметры:

‘ ‘ — строковая переменная, являющаяся именем М-файла, в котором вычисляются правые части системы ОДУ;

t 0 — начальное значение времени; tfinal — конечное значение времени;

x 0 — вектор начальных условий;

tol — задаваемая точность; по умолчанию для ode 23 tol = 1. e -3, для ode 45 tol = 1. e -6);

trace — флаг, регулирующий вывод промежуточных результатов; по умолчанию равен нулю, что подавляет вывод промежуточных результатов;

t — текущее время;

X — двумерный массив, где каждый столбец соответствует одной переменной.

Функции ode 23 и ode 45 реализуют методы Рунге — Кутты с автоматическим выбором шага, описанные в работе [2]. Такие алгоритмы используют тем большее количество шагов, чем медленнее изменяется функция. Поскольку функция ode 45 использует формулы более высокого порядка, обычно требуется меньше шагов интегрирования и результат достигается быстрее. Для сглаживания полученных процессов можно использовать функцию interp 1.

Установление заданной относительной погрешности RelTol — ODESET ( odeset ).

С помощью установления относительной погрешности RelTol контролируется количество «правильных» цифр в решении дифференциального уравнения в соответствии с общей записью , где показатель степени P есть число контролируемых цифр в решении.

Пример Уравнение Ван-дер-Поля с заданной относительной погрешностью.

С помощью функции ODESET задаются опции решателя дифуравнений с помощью соответствующих строковых символов, которых всего может быть 18. Перечень строковых символов функции ODESET можно просмотреть из командной строки, набрав в ней ODESET

% Формат записи функции odeset включает строковый служебный символ RelTol и задаваемую %величину относительной погрешности (0.1 для d 1 и 0.2 для d 2).

Рассмотрим пример решения дифференциального уравнения с начальными условиями.

Решить задачу Коши

Точное решение имеет вид

Выполним решение данной задачи с помощью программы ode 45 . Вначале в M -файл записываем правую часть уравнения, сам файл оформляем как файл-функция:

Решение будет таким

>>[ X Y ]= ode 45(@ F ,[01],[1]);

Hold on; gtext(‘y(x)’)

Формирование прямоугольной сетки на плоскости — meshgrid .

% Результатом действия функции meshgrid является формирование «основания» в плоскости XOY для построения над этим основанием пространственной фигуры.

Построение пространственных сетчатых фигур — mesh .

[ x , y ]= meshgrid (-5:0.1:5,-5:0.1:5);

Z = 1* x .* exp (- x .^2 — y .^2);% Коэффициент 1 заменить: 2, 5, 10, 20

mesh ( Z ), xlabel (‘ X ‘), ylabel (‘ Y ‘), zlabel (‘ Z ‘), title (‘ Z -поверхность’)

% Для сравнения применить plot 3( x , y , Z ), grid вместо mesh ( Z ).

[ x , y ]= meshgrid (-15:0.2:15,-15:0.2:15);

R = sqrt ( x .^2+ y .^2)+0.001; %Коэфф. 0.001 введен для исключения деления на ноль

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Для сравнения применить plot 3( x , y , Z ), grid

Сетчатая поверхность с проекциями линий постоянного уровня — mesh с .

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

Z = 1*x.* exp(-x.^2 — y.^2);

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

Сетчатая поверхность с пьедесталом плоскости отсчета на нулевом уровне— meshz .

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

[ x , y ]= meshgrid (-5:0.1:5,-5:0.1:5);

Z = 1* x .* exp (- x .^2 — y .^2);

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

В качестве примера рассмотрим известную задачу динамики популяций, где рассматривается модель взаимодействия «жертв» и «хищников», в которой учитывается уменьшение численности представителей одной стороны с ростом численности другой. Модель была создана для биологических систем, но с определенными корректурами применима к конкуренции фирм, строительству финансовых пирамид, росту народонаселения, экологической проблематике и др.

Эта модель Вольтерра-Лотка с логистической поправкой описывается системой уравнений

С условиями заданной численности «жертв» и «хищников» в начальный момент t =0.

Решая эту задачу при различных значениях a , получаем различные фазовые портреты (обычный колебательный процесс и постепенная гибель популяций) .

>>opt=odeset(‘OutputSel’,[1 2], ‘OutputFcn’, ‘odephas2’);

>> [T,X]=ode45(‘VolterraLog’, [0 10],[3 1],opt );

Имеется возможность построения и трехмерного фазового портрета с помощью функции odephas 3 . Например, решение задачи Эйлера свободного движения твердого тела:

выступает в виде:

function f = Eiler ( t , x )

f=f’;>> opt=odeset(‘OutputSel’,[1 2 3], ‘OutputFcn’, ‘odephas3’);

>> [T,X]=ode45(‘Eiler’, [0 7.25], [0 0 1], opt ); %рис.8.10

>> [T,X]=ode45(‘Eiler’, [0:0.25:7.25],[0 1 1]);

Еще один пример применения функций:

. function dn = population(t,n)

a = 0.1; f = 0.45; r = 4; q = 1.5;

dn(1) = r * n(1) — a * n(2) * n(1);

dn(2) = f * a * n(2) * n(1) — q * n(2);

opt=odeset(‘OutputSel’,[1 2], ‘OutputFcn’,’odephas2′);

[T,Y] = ode45(@lab4_f,[0 10],[n0 c0],opt);

Возвращает треугольную конечноэлементную сетку, построенную в расчётной области, геометрия которой описана в m -функции g .

Обязательным является только первый входной параметр g .

p 1, v 1,… — список необязательных ключевых («именных») параметров функции initmesh :

pk — строки символов — имена указываемых параметров;

vk — значения указываемых параметров.

Имена ключевых параметров, их назначение и допустимые значения представлены в таблице: pk Значение vk / <По умолчанию>Описание

Hmax Числовое значение < estimate >Максимальный размер треугольников

Hgrad Числовое значение <1.3>Показатель нерегулярности треугольников

Box on | < off >Генерация сетки в пределах ограниченного прямоугольника

Init on | < off >Выполнить только начальную триангуляцию границ

Jiggle off |< mean >| min Вызов функции jigglemesh

JiggleIter Числовое значение <10>Максимальное число итераций при регуляризации сетки

Параметры Box и Init связаны с работой алгоритма построения сетки. Их полезно устанавливать в ‘ on ’ для изучения алгоритма построения

сетки. Параметры Jiggle и JiggleIter используются для управления уровнем регуляризации конечноэлементной сетки (подробнее см. jigglemesh ).

p — массив узлов конечноэлементной сетки (столбцам соответствуют узлы):

— первая строка — горизонтальные координаты узлов,

— вторая строка -вертикальные координаты узлов;

e — матрица граничных элементов на границах раздела зон (см. pdegeom ):

столбцам соответствуют граничные элементы (стороны конечных элементов, принадлежащие границам раздела зон или границе расчётной области);

первые две строки — номера номера начальных и конечных узлов граничных элементов;

строки 3, 4 — длина «дуги» от начала граничного сегмента до начального и конечного узла граничного элемента, отнесённая к длине «дуги» граничного сегмента;

строка 5 — номера граничных сегментов, которым принадлежат граничные элементы;

строки 6, 7 — номера зон, примыкающих слева и справа к граничным элементам;

t — матрица треугольных конечных элементов (столбцам соответствуют треугольники):

— t (1:3, ie ) — глобальные номера узлов треугольника с номером ie ,

— t (4, ie ) — номер зоны, которой принадлежит треугольник с номером ie .

Пакет Partial Differential Equations Toolbox

Специалистов в области численных методов решения дифференциальных уравнений в частных производных несомненно заинтересует обширный пакет Partial Differential Equations Toolbox ( PDETB ). Хотя этот пакет является самостоятельным приложением и в ядро MATLAB не входит, мы приведем краткое описание некоторых его возможностей с парой примеров. Вы можете вызвать пакет с его графическим интерфейсом командой pdetool .

Поскольку ряд применений пакета — PDETB связан с проблемами анализа и оптимизации трехмерных поверхностей и оболочек, в пакет введены удобные функции для построения их графиков. Они могут использоваться совместно с функцией pdeplot , что иллюстрирует следующий пример:

В состав пакета входит ряд полезных демонстрационных примеров с именами от pdedemol до pdedemo 8. Их можно запустить как из командной строки (путем указания имени), так из окна демонстрационных примеров Demos . Рекомендуется, однако, сделать это из командной строки, так как примеры ориентированы на управление в командном режиме — в основном оно сводится к нажатию клавиши Enter для прерывания пауз, введенных для просмотра промежуточных результатов вычислений.

Рассмотрим пример pdedemoS , решающий проблему минимизации параболической поверхности решением дифференциального уравнения

-div( l/sqrt(l+grad|u| ^ 2) * grad(u) ) = 0

при граничном условии u =х*2. Ниже представлен текст файла pdedemo 3. m с убранными англоязычными комментариями:

% PDEDEM 03 Решение проблемы минимизации параболической поверхности

g =’ circleg ‘: % Единичная окружность

b =’ circleb 2′: % х ^ 2 — граничное условие

c =’ l ./ sqrt ( l + ux .*2+ uy .*2)’:

rto 1= le -3; % Погрешность вычислений решателем

pause % Пауза в вычислениях

% Решение нелинейной проблемы

pause % Пауза в вычислениях

Весьма интересны и поучительны примеры с анимацией:

pdedemo 2 — появление и распространение волн,

pdedemoS — вздутие поверхности (пузырек газа),

pdedemo 6 — колебания плоскости (гиперболическая проблема) и т. д.

Переопределение (сгущение) треугольной сетки с помощью REFINEMESH

[p1,e1,t1]= refinemesh (g,p,e,t)

Возвращает переопределённую версию треугольной конечноэлементной сетки, представленной геометрией g , матрицей узлов p , матрицей граничных элементов e и матрицей треугольников t .

g описывает геометрию PDE задачи. g может матрицей “расчленённой” геометрии или именем m -файла описания геометрии. См также decsg , pdegeom .

p , e , t — матрицы описания конечноэлементной сетки (см initmesh ).

Переопределяет сетку, а также доопределяет значения искомой функции во вновь сгенерированных узлах конечноэлементной сетки. Доопределение производится с помощью линейной интерполяции (т.е. применяются линейные функции формы).

u — узловое распределение искомой функции (величины) на непереопределённой сетке. Строкам u и столбцам p соответствуют узлы. Строкам u 1 и столбцам p 1 соответствуют узлы переопределённой сетки. Каждый столбец u интерполируется отдельно.

[p1,e1,t1]=refinemesh(g,p,e,t,u,it) или [p1,e1,t1,u1]=refinemesh(g,p,e,t,u,it)

it — список зон для переопределения сетки, если it — матрица-строка, или список треугольников, если it — матрица-столбец.

Если этот параметр задан, то сетка переопределяется (сгущается) только в указанных зонах или конечных элементах.

[p1,e1,t1]=refinemesh(g,p,e,t,u,it,mode) или [p1,e1,t1,u1]=refinemesh(g,p,e,t,u,it,mode)

mode — метод переопределения сетки (по умолчанию — “регулярное переопределение”, когда каждый переопределяемый треугольник разделяется на четыре треугольника).

Этот параметр может принимать одно из следующих значений:

— ‘ longest ’ — треугольники делятся на два так, что большая сторона делится пополам;

— ‘ regular ’ — “регулярное переопределение”.

Некоторые треугольники вне указанного набора могут также быть переопределены, чтобы сохранить там триангуляцию и её качество.

Формирование линейного массива равноотстоящих узлов LINSPACE

x = linspace(x1, x2)

x = linspace(x1, x2, n)

Функция x = linspace ( x 1, x 2) формирует линейный массив размера 1 х 100, начальным и конечным элементами которого являются точки x 1 и x 2.

Функция x = linspace ( x 1, x 2, n ) формирует линейный массив размера 1 х n , начальным и конечным элементами которого являются точки x 1 и x 2.

Решение параболической PDE задачи с помощью PARABOLIC

u1= parabolic (u0,tlist,b,p,e,t,c,a,f,d)

Возможны также следующие варианты вызова данной функции:

Здесь rtol , atol — относительная и абсолютная погрешность решателя ODE .

Производит решение скалярной PDE задачи, основанной на уравнении вида

u 0 — узловое распределение искомой величины в начальный момент времени t =0;

tlist – список моментов времени, для которых нужно вычислить решение уравнения (1);

b — имя пользовательской m -функции, вычисляющей матрицы описания граничных условий (см. pdebound );

p — массив узлов конечноэлементной сетки (столбцам соответствуют узлы):

— первая строка — горизонтальные координаты узлов,

— вторая строка — вертикальные координаты узлов;

e — матрица граничных элементов на границах раздела зон (см. initmesh , pdegeom );

t — матрица треугольных конечных элементов (столбцам соответствуют треугольники):

— t (1:3, ie ) — глобальные номера узлов треугольника с номером ie ,

— t (4, ie ) — номер зоны, которой принадлежит треугольник с номером ie .

с — массив, описывающий распределение коэффициента c в расчётной области (см. уравнение (1));

a — массив, описывающий распределение коэффициента a в расчётной области (см. уравнение (1));

f — массив, описывающий распределение правой части PDE f в расчётной области (см. уравнение (1));

d — массив, описывающий распределение коэффициента d в расчётной области (см. уравнение (1)).

Кодирование входных параметров c , a , f , d более подробно описано в assempde .

В случае скалярной PDE задачи u 1 — матрица размера ( NP , length ( tlist )), где NP — число узлов конечноэлементной сетки. Каждый столбец матрицы u 1 представляет собой узловое распределение искомой величины u в соответствующий момент времени. В случае системы PDE из N уравнений u 1 — матрица размера ( NP * N , length ( tlist )). Каждый столбец матрицы u 1 состоит из N подстолбцов, каждый из которых представляет собой узловое распределение соответствующей искомой переменной в соответствующий момент времени.