Решение дифференциального уравнения методом пристрелки

Краевые задачи

Для однозначного определения неизвестной функции \( u(x) \) уравнение (1) дополняется двумя граничными условиями на концах отрезка \( [0, l] \). Задаваться может функция \( u(x) \) (граничное условие первого рода), поток \( w(x) = −k(x) \frac (x) \) (граничное условие второго рода) или же их линейная комбинация (граничное условие третьего рода): $$ \begin \tag <2>u(0) = \mu_1, \quad u(l) = \mu_2, \end $$ $$ \begin \tag <3>−k(0) \frac (0) = \mu_1, \quad k(l) \frac (l) = \mu_2 \end $$ $$ \begin \tag <4>−k(0) \frac (0) + \sigma_1 u(0) = \mu_1, \quad k(l) \frac (l) + \sigma_2 u(l) = \mu_2. \end $$

Эллиптические уравнения второго порядка, прототипом которых является уравнение (1), используются при моделирование многих физико-механических процессов.

Кроме того,могут рассматриваться задачи с несамосопряженным оператором, когда, например, $$ \begin \tag <5>— \frac \left( k(x) \frac \right) + v(x) \frac + q(x) u = f(x), \quad 0 —>

Метод стрельбы

Рассмотрим краевую задачу для уравнения второго порядка, разрешенного относительно второй производной:

(1.41)

Будем искать решение Y = Y(x) этого уравнения на отрезке [0,1]. Любой отрезок [а, b]можно привести к этому отрезку с помощью замены переменной

Граничные условия на концах рассматриваемого отрезка примем в простейшем виде (1.37), т.е.

(1.42)

Сущность метода стрельбы заключается в сведении решения краевой задачи (1.41), (1.42) к решению последовательности задач Коши для того же уравнения (1.41) с начальными условиями

(1.43)

Здесь Y0 — точка на оси ординат, в которой помещается начало искомой интегральной кривой; α — угол наклона касательной к интегральной кривой в этой точке (рис. 1.5).

Рис. 1.5. Метод стрельбы

Считая решение задачи Коши , зависящим от параметра α, будем искать такую интегральную кривую , которая выходит из точки (0, Y0) ипопадает в точку (1, Y1). Таким образом, если , то решение задачи Коши совпадает с решением Y(x) краевой задачи. При х = 1, учитывая второе граничное условие (1.42), получаем , или

(1.44)

Например, при использовании метода деления отрезка пополам поступаем следующим образом. Находим начальный отрезок , содержащий значение α*, на концах которого функция F(x) принимает значения разных знаков. Для этого решение задачи Коши Y(x, α0) должно при х=1 находиться ниже точки Y1, а Y(x,α1) — выше. Далее, полагая , снова решаем задачу Коши при α= α2и в соответствии с методом деления отрезка пополам отбрасываем один из отрезков: или , на котором функция F(x) не меняет знак, и т.д.. Процесс поиска решения прекращается, если разность двух последовательно найденных значений а меньше некоторого наперед заданного малого числа. В этом случае полученное последним решение задачи Коши и будет принято за искомое решение краевой задачи.

Описанный алгоритм называется методом стрельбы вполне оправданно, поскольку в нем как бы проводится «пристрелка» по углу наклона интегральной кривой в начальной точке. Следует отметить, что этот алгоритм хорошо работает в том случае, если решение не слишком чувствительно к изменениям α; в противном случае мы можем столкнуться с неустойчивостью.

Для решения уравнения (1.44) используют и другие методы. В частности, одним из самых надежных является метод Ньютона. Его применение состоит в следующем. Пусть α0 — начальное приближение к α*. Построим итерационный процесс для нахождения последующих приближений αkс помощью формулы Ньютона (1.11):

.

С учетом того, что , имеем

. (1.45)

Производную в знаменателе этого выражения можно найти численно:

(1.46)

Здесь Δα — произвольное малое возмущение α.

Для вычисления правой части (1.46) нужно решить задачу Коши при , в результате чего найдем значение . Затем по формуле (1.45) находим следующее приближение αkпараметра α* и т.д. Этот итерационный процесс продолжается до тех пор, пока два последовательных приближения αk—1и αk не станут различаться меньше, чем на заданное малое число ε.

Алгоритм решения краевой задачи методом стрельбы с применением пристрелки по методу Ньютона представлен на рис. 1.6. Нахождение решения задачи Коши Y(x,α) входит в данный алгоритм в качестве отдельного модуля с входным данным α. На выходе модуля получается решение Y(x, α) в виде значений yi (i=0,1. п)в точках xi = ih, где h = l/n.

Рис. 1.6. Алгоритм метода стрельбы

Методы стрельбы могут также использоваться для решения системы уравнений. В этом случае краевая задача (а не задача Коши) может возникнуть в силу того, что значения одной части искомых функций заданы при одном значении независимой переменной (например, при х = 0), а другой — при другом (например х = 1).

Тогда «пристрелка» проводится по неизвестным значениям искомых функций при х = 0 до тех пор, пока не будут удовлетворяться соответствующие граничные условия при х = 1.

Например, рассмотрим систему двух уравнений первого порядка:

(1.47)

Граничные условия заданы в виде

(1.48)

Процесс решения этой краевой задачи методом стрельбы состоит в следующем. Выбирается некоторое α, являющееся начальным приближением для Z(0). Решается задача Коши для системы (1.47) с начальными условиями Y(0) =Y0,Z(0) = α. В результате решения при х = 1 получается некоторое значение Z(1, α) ≠ Z1. Если разность между этими величинами невелика, то найденное решение задачи Коши принимается за искомое решение краевой задачи. В противном случае находится уточненное значение αи процесс повторяется.

Таким образом, метод стрельбы может быть также использован для решения как краевых задач для уравнений высших порядков, так и систем уравнений.

Метод стрельбы для линейного дифференциального уравнения

Если обыкновенное дифференциальное уравнение второго порядка яв­ляется линейным, то есть имеет вид

(6.63)

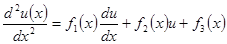
при граничных условиях, то поиск решения методом стрельбы сущест­венно упрощается.

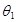
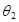
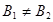
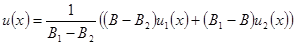
Выполнив два «пристрелочных» расчета при и , как это было опи­сано ранее, получим два решения u₁(x) и u₂(x). Если u₁(b) = B₁ и u₂(b) = B₂, причем , то решением краевой задачи будет линейная комбинация двух решений

(6.64)

Подставляя в это выражение при x = a значения u₁(a) = A и при x = b значения u₁(b) = B₁, u₂(b) = B₂, нетрудно убедиться, что оно удовле­творяет обоим исходным граничным условиям задачи.

Большое число задач, связанных с анализом физических (и не только физических) полей описываются дифференциальными уравнениями в част­ных производных. К сожалению, во многих случаях, представляющих прак­тический интерес, найти аналитическое решение таких задач трудно или практически невозможно. Это обычно обусловлено сложной формой или не­однородностью свойств области, в которой отыскивается решение.

Однако результат можно получить численно с помощью компьютера. Подходы к решению дифференциальных уравнений с частными производ­ными определяются их математической формой. Поэтому рассмотрим клас­сификацию уравнений с этой точки зрения.

Дата добавления: 2015-04-03 ; просмотров: 895 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ