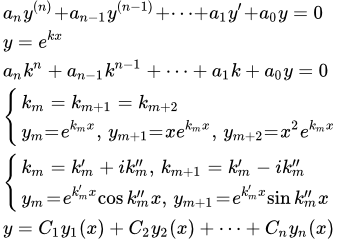Решение дифференциального уравнения при кратных корнях

Система линейных дифференциальных уравнений с постоянными коэффициентами (случай кратных корней характеристического уравнения)

Смотреть на youtube || на ИНТУИТ в качестве: высоком

Постановка задачи про кошку не корректна.

Слева в уравнение ускорение, а спава сумма сил, с размерностями путаница возникла. Нужно слева тоже вторую производную по координате умножать ещё на массу кошки и тогда все встаёт на места. А именно, известно что ускорение свободного падения не зависит от массы падающего тела (в вакууме естественно), а у Вас в задаче оно вдруг стало зависеть!

Когда мы в начале решали дифур хy’=y, то после интегрирования получили Abs(y/y0)=Abs(x/x0), ведь интеграл от dy/y (например) не просто ln y, а ln( abs(y)). Там ведь модуль. А значит, решая уравнение с модулями мы получаем два решения: y = c*x и y = — c*x (с = y0/x0). И на координатной плоскости мы получим две прямые, которые симетричные относительно начала координат.

Решение линейных однородных дифференциальных уравнений с постоянными коэффициентами

Вид общего решения

Рассмотрим линейное однородное дифференциальное уравнение с постоянными коэффициентами:
(1) .
Его решение можно получить следуя общему методу понижения порядка.

Однако проще сразу получить фундаментальную систему n линейно независимых решений и на ее основе составить общее решение. При этом вся процедура решения сводится к следующим шагам.

Ищем решение уравнения (1) в виде . Получаем характеристическое уравнение:
(2) .
Оно имеет n корней. Решаем уравнение (2) и находим его корни . Тогда характеристическое уравнение (2) можно представить в следующем виде:
(3) .
Каждому корню соответствует одно из линейно независимых решений фундаментальной системы решений уравнения (1). Тогда общее решение исходного уравнения (1) имеет вид:
(4) .

Действительные корни

Рассмотрим действительные корни. Пусть корень однократный. То есть множитель входит в характеристическое уравнение (3) только один раз. Тогда этому корню соответствует решение
.

Пусть – кратный корень кратности p . То есть
. В этом случае множитель входит в характеристическое уравнение (3) p раз:
.
Этим кратным (равным) корням соответствуют p линейно независимых решений исходного уравнения (1):
; ; ; . ; .

Комплексные корни

Рассмотрим комплексные корни характеристического уравнения (3). Выразим комплексный корень через действительную и мнимую части:
.
Поскольку коэффициенты исходного уравнения (1) действительные, то кроме корня имеется комплексно сопряженный корень
.

Пусть комплексный корень однократный. Тогда паре корней соответствуют два линейно-независимых решения уравнения (1):
; .

Пусть – кратный комплексный корень кратности p . Тогда комплексно сопряженное значение также является корнем характеристического уравнения кратности p и множитель входит в разложение на множители (3) p раз:
.
Этим 2 p корням соответствуют 2 p линейно независимых решений:
; ; ; . ;
; ; ; . .

После того как фундаментальная система линейно независимых решений найдена, по формуле (4) получаем общее решение уравнения (1).

Примеры решений задач

Пример 1

Найти общее решение однородного дифференциального уравнения седьмого порядка с постоянными коэффициентами:
.

Ищем решение в виде . Составляем характеристическое уравнение:
.
Преобразуем его:
;
;
.

Рассмотрим корни этого уравнения. Мы получили четыре комплексных корня кратности 2:
; .
Им соответствуют четыре линейно-независимых решения исходного уравнения:
; ; ; .

Также мы имеем три действительных корня кратности 3:
.
Им соответствуют три линейно-независимых решения:
; ; .

Общее решение исходного уравнения имеет вид:
.

Пример 2

Это однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Ищем решение в виде . Составляем характеристическое уравнение:
.
Решаем квадратное уравнение.
.

Мы получили два комплексных корня:
.
Им соответствуют два линейно-независимых решения:
.
Общее решение уравнения:
.

Пример 3

Найти общее решение однородного дифференциального уравнения четвертого порядка с постоянными коэффициентами:
.

Ищем решение в виде . Составляем характеристическое уравнение:
.
Выносим за скобки:
(П3.1) .
Решаем квадратное уравнение :
.
Получили два комплексных корня, которые обозначим как . Тогда . Перепишем характеристическое уравнение (П3.1) в эквивалентном виде:
.
Отсюда видно, что оно имеет два кратных корня кратности 2, и два комплексно сопряженных корня . Кратным корням соответствуют два линейно независимых решения:
;
.
Комплексно сопряженным корням , соответствуют решения
.
Общее решение:
.

Автор: Олег Одинцов . Опубликовано: 29-07-2013 Изменено: 27-10-2020