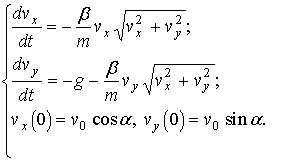Решение дифференциального уравнения в программировании

Как написать программу решения дифференциального уравнения… ( C++ )

Для численного решения обыкновенных дифференциальных уравнений различают задачи с начальными условиями (ЗНУ) и граничными условиями (ЗГУ).

Дело в том, что для полного определения искомой функции одного уравнения недостаточно. При определении первообразной из производной функции мы получим множество решений, отличающихся друг от друга свободным членом (константой С).

Поэтому, для однозначного определения данной константы С, у искомой функции должны задаваться еще граничные условия, указывающие, что делается на концах исследуемого интервала, и/или начальные условия, описывающие значение функции
в начальный момент (t = 0). Совокупность граничных и начальных условий называется краевыми условиями.

Для численного решения обыкновенных дифференциальных уравнений применяют метод Рунге-Кутта, с наиболее часто используемым 4-ым порядком точности. Давайте рассмотрим программную реализацию данного метода Рунге-Кутта, и Вы увидите, что написать программу для решения дифференциального уравнения не составляет особого труда.

Вариант решения задачи рассмотрю на следующем примере:

Условия задачи:
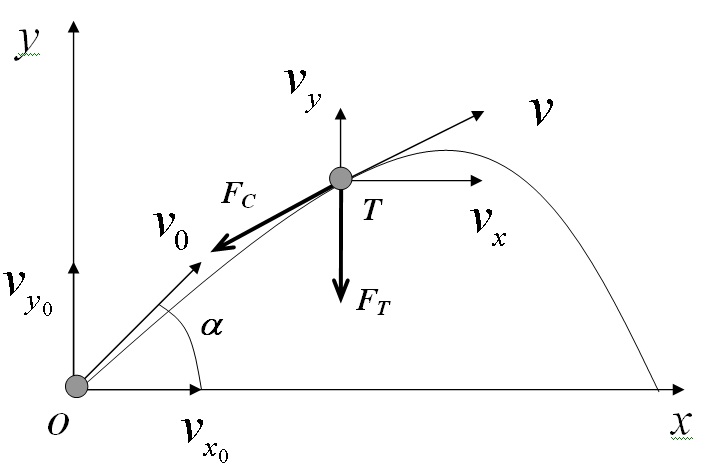
Пусть выстрел из орудия произведен с начальной скоростью V₀, под углом к горизонту α, с высоты Н₀ расположения орудия, т.к. в реальности огонь может вестись с холма или из капонира (т.е. ниже уровня земли).
Считаем, что снаряд имеет форму шара с радиусом r, изготовлен из материала, имеющего определенную плотность ρ.
Построить траекторию полета снаряда Y(x) ,
указать максимальную высоту полета H_k , дальность падения снаряда X_k и время полета t_k , построить график скорости V(t) на отрезке [0,t_k].

Таким образом, исходные данные, которые пользователь может задать на форме:
Начальная скорость V₀, м/с2
Начальная высота H₀, м
Угол выстрела α, ° (град)
Плотность материала ρ, кг/м3
Радиус r, м

При построении математической модели условимся, что ось Оx системы координат направлена горизонтально в направлении выстрела, а ось Oy — вертикально вверх. Вектор скорости снаряда V(t) за время полета будет изменяться как по величине, так и по направлению, поэтому в модели рассматриваем его проекции на координатные оси. Горизонтальную составляющую скорости в момент времени t обозначим V_x(t), а вертикальную – V_y(t).

Пусть поверхность Земли плоская. Согласно законам механики, при сделанных предположениях движения тела в горизонтальном направлении является равномерным, а в вертикальном – равнозамедленным или равноускоренным с ускорением свободного падения g.

Если с силой тяжести F_T все достаточно просто (она свой вектор не меняет ни по величине, ни по направлению), то сила лобового сопротивления F_C , действующая на снаряд, пропорциональна квадрату скорости движения тела. Обозначим через F_X и F_Y горизонтальную и вертикальную проекции вектора силы лобового сопротивления,
причем F_X/F= V_X/V, F_Y/F= V_Y/V.

Значение силы лобового сопротивления F= -b·V² (пропорционально квадрату скорости тела). Коэффициент b=0.5·C·S·ρ, где C – коэффициент лобового сопротивления (для многих задач баллистики C≈0.15), S – площадь поперечного сечения (S=πr²), ρ — плотность воздуха (ρ=1,29 кг/м3).

Решение поставленной задачи можно свести к решению системы дифференциальных уравнений

Метод Рунге-Кутта предполагает многократное вычисление значения производной искомой функции по имеющейся формуле (из уравнения), поэтому имеет смысл …

Код функций будет выглядеть так:

// функция Нахождение горизонтальной проекции скорости
//по первому уравнению системы
double Form1::fvx( double vy, double vx )
<
return -b*vx*sqrt(vx*vx+vy*vy) / m;
>

// функция Нахождение вертикальной проекции скорости
//по второму уравнению системы
double Form1::fvy( double vy, double vx )
<
return -b*vy*sqrt(vx*vx+vy*vy) / m — g;
>

Шаг интегрирования у меня задается на форме.
Сейчас нам предстоит вычислить значения нескольких функций (V_x, V_y, V ) в точках интервала с шагом. В моем примере у интервала задано начало х=0, а конечная точка интервала будет определена в процессе вычисления ( высота полета ядра стала Void Form1::Runge_Kutta(void)
<
double k1,k2,k3,k4, l1,l2,l3,l4;

pY[0]=H; pX[0]=0; pt[0]=0; //массивы-координаты: высота, дальность и время
pVx[0]=Vx; pVy[0]=Vy; pV[0]=V; //массивы- скорости: проекции на
//горизонталь и вертикаль и полная скорость (величина вектора)
bool vzbool=true;//взлет
int i=1;

//расчет по модели и заполнение массивов
while( (pY[i-1]>-0.00001 || vzbool) && i pY[i-1]) iMax=i; //сохранение номера узла с максимальной высотой
else vzbool=false;//падение

i++;
>
n=i-1; //количество реальных шагов
>

где:
int iMax; //узел с макс.высотой полета

double b; //коэф.пропорциональности Силы лобового сопротивления
double m; //масса ядра
double H; //уровень расположения орудия в момент выстрела
double V,Vx,Vy; //начальная скорость и ее проекции на оси

В результате работы этой подпрограммы произойдет численное решение задачи Коши для системы обыкновенных дифференциальных уравнений и будут получены значения функций V_x(t_i), V_y(t_i) в точках t_i=i·h, i=1,2. ; h – шаг метода.

Как видим, после получения нового значения скорости V_x(t_i)
рассчитывается координата X(t_i)=X(t_i-1)+h·V_x(t_i), где h= t_i-t_i-1 = const.
Кроме того, параллельно рассчитывается значение высоты Y(t_i)=Y(t_i-1)+h·V_y(t_i),
где h= t_i-t_i-1 = const по найденным значениям V_y(t_i).
Когда будет получено значение Y(t_i)

Общие методы программирования решения дифференциальных уравнений

Страницы работы

Содержание работы

Министерство образования РФ

Сибирский государственный технологический университет

Факультет автоматизации и информационных технологий

Кафедра автоматизации производственных процессов

Разработал: студ. гр. 24-2

__________ Захаров А.С.

__________ Устимец В.А.

Общие методы программирования решения дифференциальных уравнений

Исследованию подлежит дифф. уравнение вида .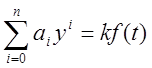

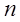
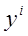
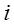
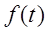
— порядок производной;

— -ая производная от искомой переменной;

-возмущение действующее на систему;

— коэффициенты уравнения.

Уравнение описывает поведение объекта под действием возмущающего воздействия.

Правая часть – возмущение, левая часть – сам объект.

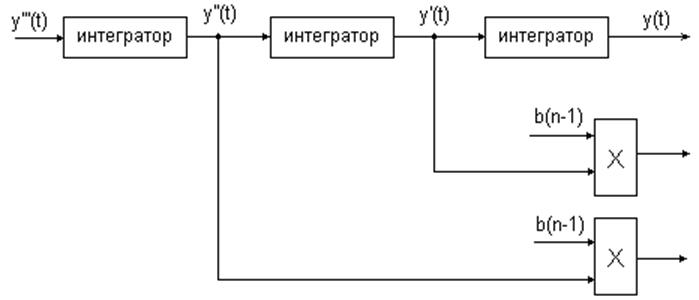
Имеется 2 алгоритма решения повысительный и понизительный. Учитывая что повысительный алгоритм имеет не высокую помехозащищённость – им пользоваться не будем. При понизительном алгоритме(метод понижения порядка производной) уравнение разрешается относительно высшей производной и приобретает вид:

, где .

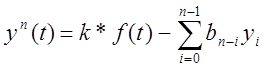
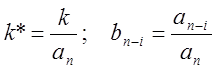
Анализируя левую часть уравнения можно предложить следующую схему её решения: принимать что значение функции левой части нам известно, тогда последовательным интегрированием получим все производные низших порядков в плоть до получения в итоге искомой переменной 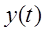. На модели данную операцию можно представить в виде цепочки модулей интеграторов, количество которых равно порядку решаемого дифф. уравнения.

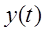
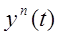
Обратим ся к правой части уравнения , отметим что она равна n-ой производной , т.е. можно утверждать что выполнив операции(математ.) правой части уравнения мы получим значение функции .

На модели данную операцию можно представить в виде модуля сумматора на вход которого поступают 2 слагаемых, 1-ое слагаемое равное возмущению действующему на систему, на модели она может быть представлена в виде спец. модуля – источника возмущения : второе слагаемое равно сумме включающую произведение искомой переменной и её производных достепени включительно, на коэффициенты дифф. уравнения разрешённого относительно старшей производной. На модели составляющая второго слагаемое могут быть представлены модулями умножителями, на вход каждого из которых будут поступать значение коэффициента и значение производной .

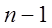
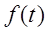
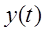
Рассмотренный алгоритм схему с кольцевой структурой , которая после установки начальных условий и её возбуждениявозмущением работает как единое целоевыдовая на выходе искомую функцию которая и подлежит дальнейшему исследованию.

Исследование графической модели

Набрать решение дифференциального уравнения:

В качестве исходных значений для исследования принять:

начальные условия y’(0) = 0;

возмущения действующие на объект :

период моделирования 0 – 20 с.

Провести исследование системы при различных значениях параметров.

Решение поставленной задачи

Для решения поставленной задачи будем использовать метод понижения порядка производной. Разработка в несколько этапов:

1. Этап – разрешим уравнение относительно старшей производной

Полученое уравнение представляет собой структурную схему в которой каждый элемент математической операции соответствует определённое звено.

2. Этап – средствами SIMULINK соберём блок схему решения левой части последнего уравнения которая должна формировать сигнал производной и выходной переиенной. Представим её в виде цепочки из 2x интеграторов, поскольку данная задача требует рашения с начальными условиями выбираем настройку интеграторовна внешние начальные условия.

Блок – схема решения данного уравнения

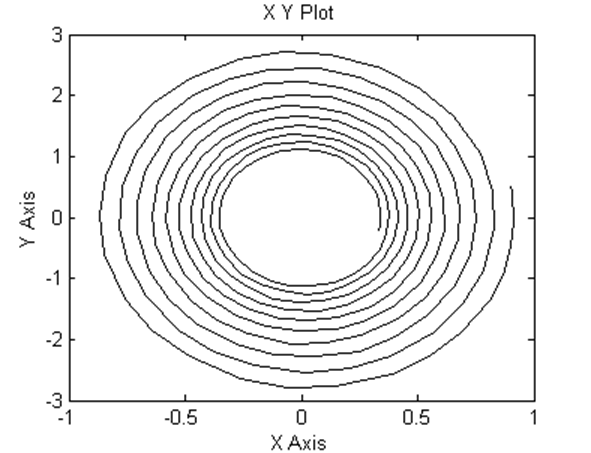
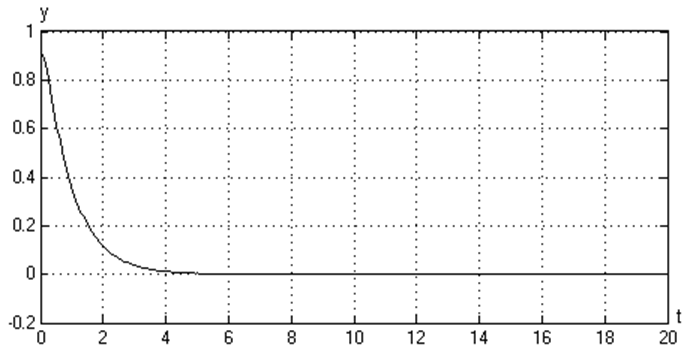
Фазовый портрет (при а₁= 0,1)

Фазовый портрет (при а­₁= 1)

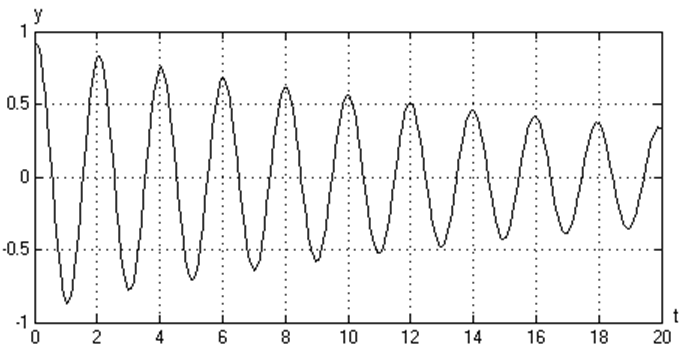
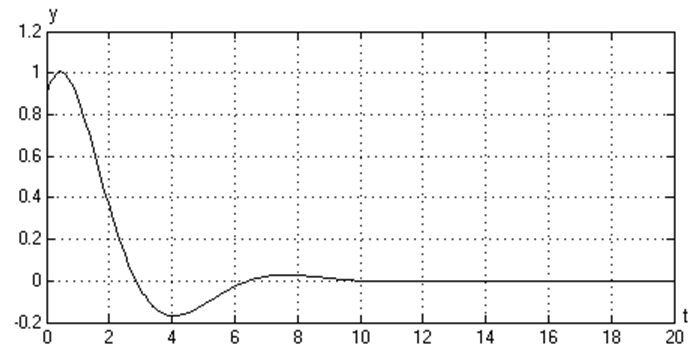
График зависимости y(t) (при а₁=0,1, а₀=10)

Фазовый портрет (при а­₁= 10)

График зависимости y(t) (при а₁=1, а₀=10)

График зависимости y(t) (при а₁=10, а₀=10)

График зависимости y(t) (при а₁=1, а₀=1)

Модель одноемкостного объекта

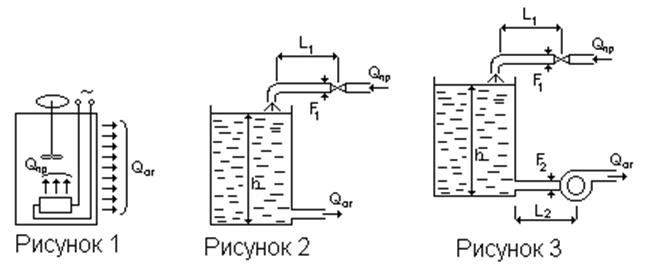
Рассматриваются три типовых объекта, которые могут являться объектами регулирования в различных технологических цепочках химического производства: термостат (рисунок 1); емкость, приток и отток которой происходит самотеком (рисунок 2); емкость, приток которой происходит самотеком, а отток при помощи насоса (рисунок 3).

Рисунок 1 – Термостат

Рисунок 2 – Емкость, приток и отток которой происходит самотеком

Рисунок 3 – Емкость, приток которой происходит самотеком, а отток при помощи насоса

Модель объекта будем составлять как модель объекта регулирования. При этом в качестве регулируемого параметра в первом случае будет температура жидкости в емкости, а во втором и третьем – уровень жидкости в баке h.

Рассмотрим 1 случая, при котором в качестве регулируемого параметра выступает температура жидкости в емкости.

Запишем уравнение баланса:

. (1)

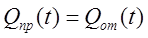
В случае нарушения баланса часть энергии соберется в емкости. Уравнение баланса примет вид:

, (2)

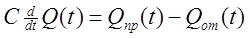
где Q_пр – приток тепла, ккал/с;

Q_от – отток тепла, ккал/с;

Q(t) – температура, о С;

С – теплоемкость среды в объекте, ккал/град.

Принимая, что отток тепла зависит от температуры и, полагая эту зависимость линейной, получим: 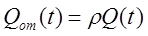. (3)

где r — коэффициент самовыравнивания, ккал/град.

Смысл названия коэффициента самовыравнивания состоит в том, что в случае если этот коэффициент больше нуля, от объект сам, без внешнего воздействия всегда приходит к некоторому установившемуся состоянию, причем, тем быстрее и тем с меньшей статической ошибкой, чем больше этот коэффициент.

Подставляя уравнение (3) в уравнение (2), получим дифференциальное уравнение, описывающее поведение объекта:

. (4)

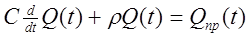
Преобразуем полученное уравнение к виду:

. (5)

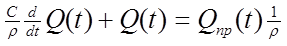
Обозначив С/r через Т_о, 1/r через К получим выражение:

, (6)

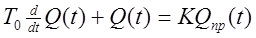
где Т_о – постоянная времени объекта;

К – коэффициент усиления объекта.

Принимая обобщенные обозначения Q(t)=y и Q_пр(t)=х, запишем:

. (7)

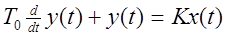
Как видно, моделью одноемкостного объекта может служить дифференциальное уравнение первого порядка.

Нахождение дифференциального уравнения реального объекта

Определяющими переменными для дифференциального уравнения являются величины T_o, K и x(t).

Постоянную времени технологического объекта можно принимать как отношение объема аппарата (V, м 3 ) к скорости движения рабочей среды через аппарат (v, м/с).

Степень самовыравнивания определяю двумя путами: из анализа физических характеристик процесса или на основании опытных данных. В последнем случае степень самовыравнивания определяют по величине коэффициента передачи объекта:

,

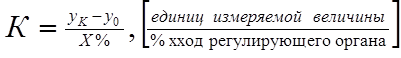
где у_К – конечное значение, которое приобретает измеряемая величина при возмущающем воздействии Х.

Моделирование объекта в Matlab

Создадим 2 примера реализации данной модели в Matlab.

Разрешим уравнение (7) относительно старшей производной:

.

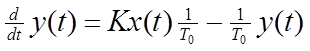
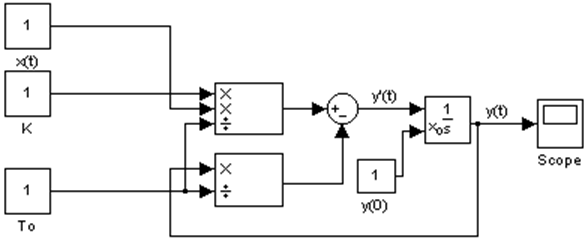
Полученное уравнение в Matlab можно изобразить в виде:

Рисунок 4 – Модель одноемкостного объекта

Запишем передаточную функцию данного объекта:

.

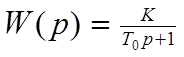
Численное решение обыкновенных дифференциальных уравнений (ОДУ) в Python

Рассмотрены приемы решения обыкновенных дифференциальных уравнений (ОДУ) с помощью модуля scipy.integrate языка Python

Краткое описание модуля scipy.integrate

Модуль scipy.integrate имеет две функции ode() и odeint(), которые предназначены для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (т.е. задача Коши).

Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.

Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат

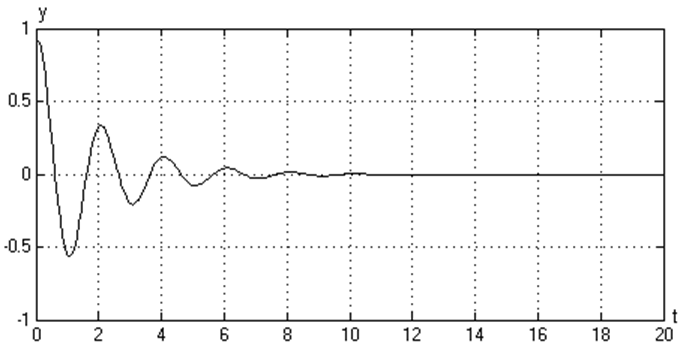
Решение одного ОДУ

Допустим надо решить диф. уравнение 1-го порядка

Получилось что-то такое:

Решение системы ОДУ

Пусть теперь мы хотим решить (автономную) систему диф. уравнений 1-го порядка

Выходной массив w состоит из двух столбцов — y1(t) и y2(t).

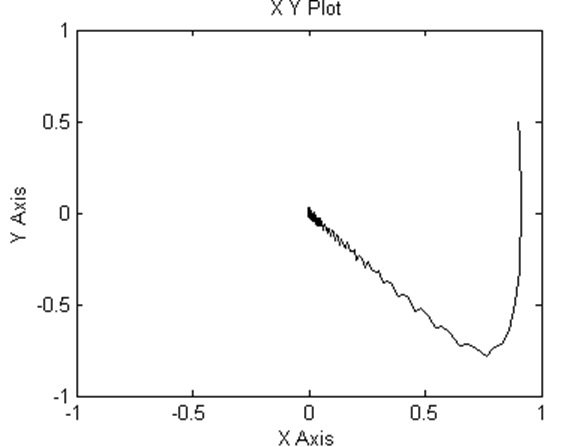
Также без труда можно построить фазовые траектории: