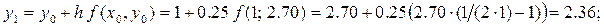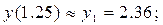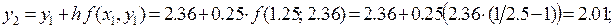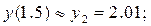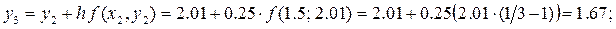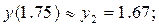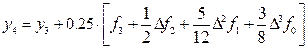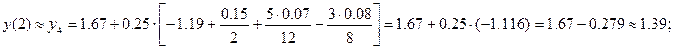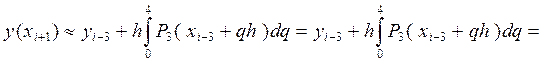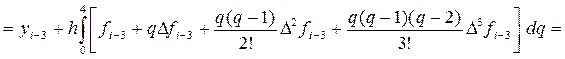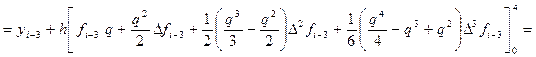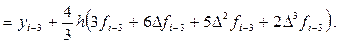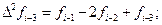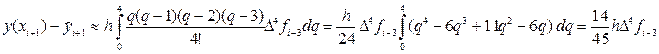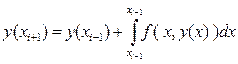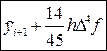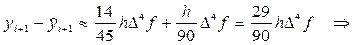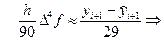Решение дифференциальных уравнений методом эйлера и адамсам

Задачи с начальными условиями для систем обыкновенных дифференциальных уравнений

Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений $$ \begin \tag <1>\frac &= f_i (t, u_1, u_2, \ldots, u_n), \quad t > 0\\ \tag <2>u_i(0) &= u_i^0, \quad i = 1, 2, \ldots, m. \end $$

Используя векторные обозначения, задачу (1), (2) можно записать как задачу Коши $$ \begin \tag <3>\frac> &= \pmb(t, \pmb), \quad t > 0, \\ \tag <4>\pmb(0) &= \pmb_0 \end $$ В задаче Коши необходимо по известному решению в точке $ t = 0 $ необходимо найти из уравнения (3) решение при других $ t $.

Численные методы решения задачи Коши

Существует большое количество методов численного решения задачи (3), (4). Вначале рассмотрим простейший явный метод Эйлера и его программную реализацию. Затем будут представлены методы Рунге—Кутта и многошаговые методы.

При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.

Идея численных методов решения задачи (3), (4) состоит из четырех частей:

1. Вводится расчетная сетка по переменной $ t $ (время) из $ N_t + 1 $ точки $ t_0 $, $ t_1 $, $ \ldots $, $ t_ $. Нужно найти значения неизвестной функции $ \pmb $ в узлах сетки $ t_n $. Обозначим через $ \pmb^n $ приближенное значение $ \pmb(t_n) $.

2. Предполагаем, что дифференциальное уравнение выполнено в узлах сетки.

3. Аппроксимируем производные конечными разностями.

4. Формулируем алгоритм, который вычисляет новые значения $ \pmb^ $ на основе предыдущих вычисленных значений $ \pmb^k $, $ k 0 $ при $ \tau\to 0 $.

Явный метод Эйлера

Проиллюстрируем указанные шаги. Для начала введем расчетную сетку. Очень часто сетка является равномерной, т.е. имеет одинаковое расстояние между узлами $ t_n $ и $ t_ $: $$ \omega_\tau = \< t_n = n \tau, n = 0, 1, \ldots, N_t \>. $$

Затем, предполагаем, что уравнение выполнено в узлах сетки, т.е.: $$ \pmb^\prime (t_n) = \pmb(t_n, u(t_n)), \quad t_n \in \omega_\tau. $$

Заменяем производные конечными разностями. С этой целью, нам нужно знать конкретные формулы, как производные могут быть аппроксимированы конечными разностями. Простейший подход заключается в использовании определения производной: $$ \pmb^\prime(t) = \lim_ <\tau \to 0>\frac<\pmb(t+\tau) — \pmb(t)><\tau>. $$

В произвольном узле сетки $ t_n $ это определение можно переписать в виде: $$ \begin \pmb^\prime(t_n) = \lim_ <\tau \to 0>\frac<\pmb(t_n+\tau) — \pmb(t_n)><\tau>. \end $$ Вместо того, чтобы устремлять шаг сетки к нулю, мы можем использовать малый шаг $ \tau $, который даст численное приближение $ u^\prime(t_n) $: $$ \begin \pmb^\prime(t_n) \approx \frac<\pmb^ — \pmb^><\tau>. \end $$ Такая аппроксимация известна как разностная производная вперед и имеет первый порядок по $ \tau $, т.е. $ O(\tau) $. Теперь можно использовать аппроксимацию производной. Таким образом получим явный метод Эйлера: $$ \begin \tag <5>\frac<\pmb^ — \pmb^n> <\tau>= \pmb(t_n, \pmb^). \end $$

Четвертый шаг заключается в получении численного алгоритма. Из (5) следует, что мы должны знать значение $ y^n $ для того, чтобы решить уравнение (5) относительно $ y^ $ и получить формулу для нахождения приближенного значения искомой функции на следующем временном слое $ t_ $: $$ \begin \tag <6>\pmb^ = \pmb^n + \tau \pmb(t_n, \pmb^) \end $$

При условии, что у нас известно начальное значение $ \pmb^0 = \pmb_0 $, мы можем использовать (6) для нахождения решений на последующих временных слоях.

Программная реализация явного метода Эйлера

Выражение (6) может быть как скалярным так и векторным уравнением. И в скалярном и в векторном случае на языке Python его можно реализовать следующим образом

При решении системы (векторный случай), u[n] — одномерный массив numpy длины $ m+1 $ ($ m $ — размерность задачи), а функция F должна возвращать numpy -массив размерности $ m+1 $, t[n] — значение в момент времени $ t_n $.

Таким образом численное решение на отрезке $ [0, T] $ должно быть представлено двумерным массивом, инициализируемым нулями u = np.zeros((N_t+1, m+1)) . Первый индекс соответствует временному слою, а второй компоненте вектора решения на соответствующем временном слое. Использование только одного индекса, u[n] или, что то же самое, u[n, :] , соответствует всем компонентам вектора решения.

Функция euler решения системы уравнений реализована в файле euler.py:

Строка F_ = lambda . требует пояснений. Для пользователя, решающего систему ОДУ, удобно задавать функцию правой части в виде списка компонент. Можно, конечно, требовать чтобы пользователь возвращал из функции массив numpy , но очень легко осуществлять преобразование в самой функции решателе. Чтобы быть уверенным, что результат F будет нужным массивом, который можно использовать в векторных вычислениях, мы вводим новую функцию F_ , которая вызывает пользовательскую функцию F «прогоняет» результат через функцию assaray модуля numpy .

Неявный метод Эйлера

При построении неявного метода Эйлера значение функции $ F $ берется на новом временном слое, т.е. для решении задачи (5) используется следующий метод: $$ \begin \tag <7>\frac<\pmb^ — \pmb^n> <\tau>= \pmb(t_, \pmb^). \end $$

Таким образом для нахождения приближенного значения искомой функции на новом временном слое $ t_ $ нужно решить нелинейное уравнение относительно $ \pmb^ $: $$ \begin \tag <8>\pmb^ — \tau \pmb(t_, \pmb^) — y^n = 0. \end $$

Для решения уравнения (8) можно использовать, например, метод Ньютона.

Программная реализация неявного метода Эйлера

Функция backward_euler решения системы уравнений реализована в файле euler.py:

Отметим, что для нахождения значения u[n+1] используется функция fsolve модуля optimize библиотеки scipy . В качестве начального приближения для решения нелинейного уравнения используется значение искомой функции с предыдущего слоя u[n] .

Методы Рунге—Кутта

Одношаговый метод Рунге—Кутта в общем виде записывается следующим образом: $$ \begin \tag <9>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^s b_i \pmb_i, \end $$ где $$ \begin \tag <10>\pmb_i = \pmb\left( t_n + c_i\tau, \pmb^n + \tau \sum_^s a_\pmb_j \right), \quad i = 1, 2, \ldots, s. \end $$ Формула (9) основана на $ s $ вычислениях функции $ \pmb $ и называется $ s $-стадийной. Если $ a_ = 0 $ при $ j \geq i $ имеем явный метод Рунге—Кутта. Если $ a_ = 0 $ при $ j > i $ и $ a_ \ne 0 $, то $ \pmb_i $ определяется неявно из уравнения $$ \begin \tag <11>\pmb_i = \pmb\left( t_n + c_i\tau, \pmb^n + \tau \sum_^ a_\pmb_j + \tau a_ \pmb_i \right), \quad i = 1, 2, \ldots, s. \end $$ О таком методе Рунге—Кутта говорят как о диагонально-неявном.

Одним из наиболее распространенных является явный метод Рунге-Кутта четвертого порядка: $$ \begin \tag <12>\pmb_1 & = \pmb(t_n, \pmb^n), &\quad \pmb_2 &= \pmb\left( t_n + \frac<\tau><2>, \pmb^n + \tau \frac<\pmb_1> <2>\right),\\ \pmb_3 &= \pmb\left( t_n + \frac<\tau><2>, \pmb^n + \tau \frac<\pmb_2> <2>\right), &\quad \pmb_4 &= \pmb\left( t_n + \tau, \pmb^n + \tau \pmb_3 \right),\\ \frac<\pmb^ -\pmb^n> <\tau>&= \frac<1> <6>(\pmb_1 + 2\pmb_2 + 2\pmb_3 + \pmb_4) & & \end $$

Многошаговые методы

В методах Рунге—Кутта в вычислениях участвуют значения приближенного решения только в двух соседних узлах $ \pmb^n $ и $ \pmb^ $ — один шаг по переменной $ t $. Линейный $ m $-шаговый разностный метод записывается в виде $$ \begin \tag <13>\frac<1> <\tau>\sum_^m a_i \pmb^ = \sum_^ b_i \pmb(t_, \pmb^), \quad n = m-1, m, \ldots \end $$ Вариант численного метода определяется заданием коэффициентов $ a_i $, $ b_i $, $ i = 0, 1, \ldots, m $, причем $ a_0 \ne 0 $. Для начала расчетов по рекуррентной формуле (13) необходимо задать $ m $ начальных значений $ \pmb^0 $, $ \pmb^1 $, $ \dots $, $ \pmb^ $ (например, можно использовать для их вычисления метод Эйлера).

Различные варианты многошаговых методов (методы Адамса) решения задачи с начальными условиями для систем обыкновенных дифференциальных уравнений могут быть получены на основе использования квадратурных формул для правой части равенства $$ \begin \tag <14>\pmb(t_) — \pmb(t_n) = \int_^> \pmb(t, \pmb) dt \end $$

Для получения неявного многошагового метода используем для подынтегральной функции интерполяционную формулу по значениям функции $ \pmb^ = \pmb(t_, \pmb^) $, $ \pmb^n $, $ \dots $, $ \pmb^ $, т.е. $$ \begin \tag <15>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^ b_i \pmb(t_, \pmb^) \end $$

Для интерполяционного метода Адамса (15) наивысший порядок аппроксимации равен $ m+1 $.

Для построения явных многошаговых методов можно использовать процедуру экстраполяции подынтегральной функции в правой части (14). В этом случае приближение осуществляется по значениям $ \pmb^n $, $ \pmb^ $, $ \dots $, $ \pmb^ $ и поэтому $$ \begin \tag <16>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^ b_i \pmb(t_, \pmb^) \end $$

Для экстраполяционного метода Адамса (16) погрешность аппроксимации имеет $ m $-ый порядок.

На основе методов Адамса строятся и схемы предиктор–корректор. На этапе предиктор используется явный метод Адамса, на этапе корректора — аналог неявного метода Адамса. Например, при использовании методов третьего порядка аппроксимации в соответствии с (18) для предсказания решения положим $$ \frac<\pmb^ — \pmb^n> <\tau>= \frac<1> <12>(23 \pmb^ -16\pmb^ + 5\pmb^). $$ Для уточнеия решения (см. (17)) используется схема $$ \frac<\pmb^ — \pmb^n> <\tau>= \frac<1> <24>(9\pmb^ + 19\pmb^ — 5\pmb^ + \pmb^). $$ Аналогично строятся и другие классы многошаговых методов.

Жесткие системы ОДУ

При численном решении задачи Коши для систем обыкновенных дифференциальных уравнений (3), (4) могут возникнуть дополнительные трудности, порожденные жесткостью системы. Локальные особенности поведения решения в точке $ u = w $ передаются линейной системой $$ \begin \frac

= \sum_^ \frac<\partial f_i> <\partial u_j>(t, w) v + \bar(t), \quad t > 0. \end $$
Пусть $ \lambda_i(t) $, $ i = 1, 2, \ldots, m $ — собственные числа матрицы $$ \begin A(t) = \< a_(t) \>, \quad a_(t) = \frac<\partial f_i><\partial u_j>(t, w). \end $$ Система уравнений (3) является жесткой, если число $$ \begin S(t) = \frac <\max_<1 \leq i \leq m>|Re \lambda_i(t)|> <\min_<1 \leq i \leq m>|Re \lambda_i(t)|> \end $$ велико. Это означает, что в решении присутствуют составляющие с сильно различающимися масштабами изменения по переменной $ t $.
Для численное решения жестких задач используются вычислительные алгоритмы, которые имеют повышенный запас устойчивости. Необходимо ориентироваться на использование $ A $-устойчивых или $ A(\alpha) $-устойчивых методов.
Метод называется $ A $-устойчивым, если при решении задачи Коши для системы (3) область его устойчивости содержит угол $$ \begin |\arg(-\mu)| —>
Задача Коши. Метод Адамса
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования ‹‹Национальный исследовательский Нижегородский государственный университет
Кафедра кристаллографии и экспериментальной физики
ПО УЧЕБНОЙ ПРАКТИКЕ
студент 2 курса
г. Нижний Новгород
1.1 Задача Коши для обыкновенных дифференциальных уравнений первого порядка
1.2 Методы решения задачи Коши
1.3 Метод Адамса
2. Практическая часть
1.1 ЗАДАЧА КОШИ ДЛЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 1-ОГО ПОРЯДКА
Пусть дано обыкновенное дифференциальное уравнение первого порядка вида yfx,y, (1)
где f(x,y)непрерывная функция двух переменных и дифференцируемая по у. Решением данного уравнения называется функция y=(x) , непрерывно дифференцируемая на некотором конечном или бесконечном множестве и обращающая на нём данное уравнение в тождество (x)f(x,(x)).
Общее решение записывается в виде функции y (x,Cₒ) с произвольной числовой постоянной C .
Частное решение y(x,Cₒ) получается из общего решения при конкретном значении числового параметра CCₒ . Для выделения частного решения обычно ставится условие, которому должно удовлетворять это решение: у=yₒ при х=xₒ , которое называется начальным условием, а точка (хₒ,уₒ)– начальной точкой.
Задача Коши состоит в следующем: найти решение уравнения yfx,y в виде функции у(х), удовлетворяющей начальному условию: у(хₒ)=уₒ .
Геометрически это означает, что требуется найти интегральную кривую проходящую через заданную точку Мₒ(хₒ,уₒ) при выполнения равенства yfx,y.
1.2 МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ
Наиболее мощными и универсальными методами решения обыкновенных дифференциальных уравнений являются численные методы, позволяющие получать решения тогда, когда традиционные, классические, методы не помогают.
Среди численных методов решения обыкновенных дифференциальных уравнений одним из важнейших является метод конечных разностей.
Метод конечных разностей основывается:
1) на замене непрерывной области определения решения D дискретным множеством точек, называемым сеткой ω _h ;
2) на замене непрерывных функций дискретными (сеточными), определенными на введенной сетке изменения аргумента;
3) на замене производных, входящих в уравнение, конечными разностями. В результате вместо дифференциального уравнения получается конечно-разностное уравнение, определенное в узлах разностной сетки. Решение его сводится к отысканию значений сеточной функции в узлах сетки.
Методы численного решения задачи Коши для обыкновенных дифференциальных уравнений разделяют на два класса:
1) одноступенчатые методы, использующие данные о решении только в одной точке;
2) многоступенчатые, или многошаговые, методы, не требующие много повторных вычислений функций f(x,у), использующие данные о решении в нескольких точках, что вынуждает применять одношаговые методы для запуска метода и при изменении шага интегрирования. Это методы прогноза-коррекции, Адамса и другие.
1.3 МЕТОД АДАМСА
Метод Адамса относится к методам, в которых вычисление вычисление искомой функции в точке х _i ₊₁ зависит от значения этой функции в предыдущих точках, например, x _i _— _k , x _i _— _k ₊₁ . x _i _-1 , x _i . Такие методы называются многошаговыми.
Для вычисления у _i ₊₁ нужно проинтегрировать обе части уравнения уꞌ= f ( x , y ) от x _i до x _i ₊₁ :
Воспользуемся для разложения 2-ой интерполяционной формулой Ньютона, где q _i = => x = hq _i + x _i => dx = hdq . Подставим получившиеся преобразования в (2) и преобразуем:
∆ 2 yꞌ _i _-2 +∆ 3 yꞌ _i _-3 — интерполяционный полином Ньютона
Формула y _i ₊₁ = y _i + (3) называется расчётной формулой интерполяционного метода Адамса.
2. ПРАКТИЧЕСКАЯ ЧАСТЬ
Данную задачу мы решали с помощью метода Адамса через Рунге-Кутта.
рис.1. Первый блок программы
На рисунке 1 представлено начало программы. Первым делом мы задали функцию yꞌ = f ( x , y ).
n =100 — количество точек;
х= <0>и y = <0>— списки, состоящие из нулевых элементов. Задаём их именно так, чтобы не было накопления старых значений.
spic =<<0,0>> — матрица из нулевых элементов х,у.
рис.2. Блок программы для расчёта х _i
Рисунок 2: цикл For для расчёта i -ого элемента х, начиная с 1-ого и заканчивая n -ым ( n соответствует количеству точек).
AppendTo [ x , t ] — добавляет элемент t в конец списка х (список х модифицируется).
рис.3. Расчёт коэффициентов с помощью метода Рунге-Кутта
Метод Рунге-Кутта является одним из способов решения задачи Коши обыкновенных дифференциальных уравнений. Метод Адамса является сочетанием методов Эйлера и Рунге-Кутта.
Нахожу приближенные значения задачи Коши для с помощью метода Рунге-Кутта (коэффициента k ₁ , k ₂ , k ₃ , k ₄ ).
Цикл For начинается с первого, а заканчивается четвёртым элементом, так как мне нужно посчитать четыре коэффициента. Получила многочлен t . Так же добавляю полученный элемент t в конец списка у — за эту операцию отвечает функция AppendTo [ y , t ].
Сравнивая методы Рунге-Кутты четвертого порядка точности и метод Адамса при k=3так же четвертого порядка точности, видно, что на каждом шаге метод Адамса требует вычисления одного значения функции f(x,y), а метод Рунге-Кутты- четырех вычислений значений функции. Но, метод Рунге-Кутты не требует знания нескольких начальных значений и позволяет менять шаг следования точек в любой момент вычисления.
рис.4. Метод Адамса
Сам метод Адамса начинается с четвёртого элемента, а заканчивается n -ым ( n соответствует числу точек (последним)).
Следующим этапом программируем формулу (3) (п.1.3 ‹‹МЕТОД АДАМСА››).
Модифицируем список — добавляем посчитанные значения в конец списка у.
Делаем список t , состоящий из двух элементов х и у ( x [[ i ]], y [[ i ]])
Объединяем нулевой список с полученным.
рис.6. Проверка с помощью встроенной функции
Выполним проверку заданного уравнения с помощью встроенной функции DSolve (функция, которая применяется для решения обыкновенных дифференциальных уравнений, имеющих аналитические решения)
рис.7. Построение графиков
1. График состоящий из точек полученного списка из элементов x [[ i ]], y [[ i ]]. Сделаем эти точки розового цвета ( RGB С olor и номер цвета)
2. График проверки решения обыкновенных дифференциальных уравнений
3.Объединение двух графиков (1,2).
Для того, чтобы вывести результат решения дифференциального уравнения у’= f ( x ,у), нужно зажать клавиши Enter + Shift .
рис.8. График решения методом Адамса
На рисунке 8 изображен график решения уравнения f ( x ,у)= x +у (данная функция изображена на рис.1) методом Адамса.
рис.9. График проверки обыкновенных дифференциальных уравнений
На рисунке 9 изображен график решения дифференциального уравнения с помощью встроенной функции.
рис.10. Объединение двух графиков (8,9)
Объединяем график проверки решения дифференциального уравнения и график решения уравнения методом Адамса.
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ. Пример. Решить экстраполяционным методом Адамса уравнение:
Пример. Решить экстраполяционным методом Адамса уравнение:
(33)
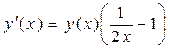
с начальным условием y(1) = 2.70 на интервале [1; 2.25], принимая h = 0.25 . В качестве разгонных точек x₀, x₁, x₂, x₃ и соответствующих решений y₀, y₁, y₂, y₃ для реализации метода Адамса взять значения, полученные методом Эйлера в точках: x₁, x₂, x₃. Все вычисления вести с тремя верными в узком смысле знаками.
Решение. Вычислительная схема экстраполяционного метода Адамса определяется выражением:
(10)
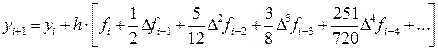
Поскольку на основе разгонных данных для функции f (x_i, y_i) можно вычислить только конечные разности до третьего порядка включительно: Df_i; D 2 f_i; D 3 f_i, то для решения данной задачи формула (10) перепишется в виде:
Далее в соответствии с условием задачи по методу Эйлера на интервале
[1; 1.75] с шагом h = 0.25 необходимо найти приближённые значения решения y₁, y₂, y₃ данного уравнения. Для этого используется численная схема, определяемая уравнением:
, i = 0, 1, …, n
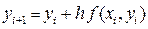
Очевидно, что для получения необходимых разгонных данных метода Адамса: y₁ » y(1.25); y₂ » y(1.5); y₃ » y(1.75) по методу Эйлера необходимо реализовать трёхшаговый вычислительный процесс.
Шаг 1:
В результате находим:
Шаг 2:
В результате находим:
Шаг 3:
В результате находим:
Таким образом, в качестве разгонных значений для метода Адамса имеем следующие приближённые значения решения:
Далее в соответствии с требованиями метода Адамса на основе полученных расходных данных вычислим приближённые значения функции:
f (x_i, y_i) = 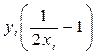i = 0, 1, 2, 3;
Далее для реализации метода Адамса на основе имеющихся данных составим для функции f (x_i, y_i) таблицу конечных разностей:
i x_i y_i f _i Df _i D 2 f _i D 3 f _i
1.00 1.25 1.50 1.75 2.00 2.25 2.70 2.36 2.01 1.67 1.39 1.14 — 1.35 — 1.42 — 1.34 — 1.19 — 1.04 — 0.7 0.08 0.15 0.15 0.15 0.07 0.00 — 0.08 — 0.07
Теперь по формуле 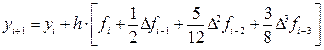при h = 0.25 и i = 3
получим:
и подставляя из таблицы 2 соответствующие значения функции f (x₃, y₃) = f₃ = — 1.19 и её конечных разностей: Df₂ = 0.15; D 2 f₁ = 0.07; D 3 f₀ = — 0.08; (которые в таблице 2 подчёркнуты) окончательно получим:
Далее на основе полученного приближённого значения y₄ = 1.39; вычисляем значение f (x₄, y₄) = f(2.00; 1.39) = f₄ = — 1.04; и конечные разности Df₃ = 0.15; D 2 f₂ = 0.00;
D 3 f₁ = — 0.07; (которые в таблице 2 обведены рамкой) окончательно получим при i = 4:
;
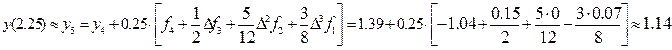
Этот вычислительный пошаговый процесс можно продолжать и далее…
Отметим, что для получения более точных результатов разгонные значения для метода Адамса целесообразно было бы получить более точным методом, например, методом Рунге-Кутта четвёртого порядка. Здесь мы использовали метод Эйлера исключительно из-за его просты.
§5. Метод Милначетвёртого порядка.
Ещё одним методом прогноза и коррекции, используемым на практике, является метод Милна, в рамках которого имеется две формулы – первая и вторая формулы Милна, которые используются соответственно для предсказания и уточнения (коррекции) искомого решения y(x) задачи Коши.
5.1 Первая формула Милна – формула предсказания.
Снова строим численный методы решения начальной задачи.
y_i_—₃ » y(x_i_—₃), y_i_—₂ » y(x_i_—₂), y_i_—₁ » y(x_i_—₁), y_i » y(x_i). f_i_—₃ = f (x_i_—₃, y_i_—₃) » f (x_i_—₃, y(x_i_—₃) ), f_i_—₂ = f (x_i_—₂, y_i_—₂) » f (x_i_—₂ y(x_i_—₂) ), f_i_—₁ = f (x_i_—₁, y_i_—₁) » f (x_i_—₁, y(x_i_—₁) ), f_i = f (x_i, y_i) » f (x_i, y(x_i) ).
(34)
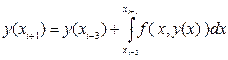
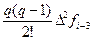
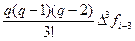
P₃(x _i_—₃ + qh) = f _i_—₃+ qD f _i_—₃ + + . (35)
При подстановке в выражение (34) полинома (35), зависящего от переменной 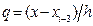, в интеграле формулы (34) необходимо сделать замену переменной:
x ® x _i_—₃ + qh; в соответствии с которой:
.
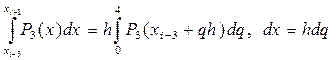
Поэтому в результате выражение (34) перепишется в следующем виде:
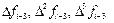
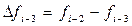
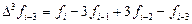
Отсюда, выразив конечные разности через значения функции f (x, y):
;
,
получим первую явную формулу (предсказания) Милна четвёртого порядка:
, (36)
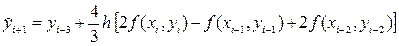
которая, очевидно, является экстраполяционной, поскольку делает предсказание решения y (x_i₊₁) на основе интерполяционного полинома, построенного по узлам
x_i_–₃, x _i–₂, x_i_–₁, x_i. Далее в лекции, полученные по формуле предсказания (36) приближённые значения y_i для искомого решения y(x _i), будем обозначать как .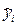
Оценка шаговой погрешности первой формулы Милна.
Главный член локальной погрешности формулы (36) можно найти при интегрировании первого из неучтённых в (35) слагаемого интерполяционного полинома Ньютона:
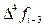
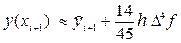
Считая значения четвёртых разностей примерно одинаковым в используемой области таблицы конечных разностей функции f_i, опустим индекс у функции f в записи ; в результате получим следующее приближённое представление решения в точке x _i₊₁ на основе первой формулы Милна:
(37)
5.2 Вторая формула Милна – формула уточнения.
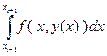
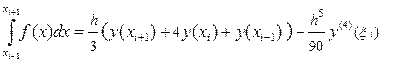
и применим к интегралу простейшую формулу Симпсона:
, где x_iÎ(x_i-1, x_i+1).
В результате получим:
(38)
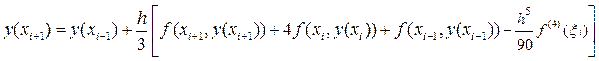
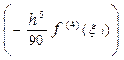
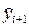
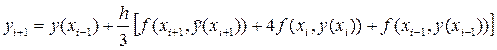
Отбрасывая в формуле (38) слагаемое , характеризующее ошибку квадратурной формулы Симпсона и заменяя значения решения y(x _i_—₁) и y(x _i) известными приближёнными значениями y _i_—₁ и y _i, а стоящее в правой части (38) в качестве аргумента функции f(x _i₊₁, y(x _i₊₁)) значение y(x_i₊₁) значением , полученным по первой (явной) формуле Милна (36), приходим ко второй интерполяционной (и неявной) формуле Милна – формуле уточнения.
(39)
Оценка шаговой погрешности второй формулы Милна.
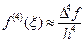
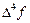
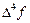
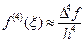
Для вывода приближённой оценки шаговой погрешности метода Милна воспользуемся приближённым равенством, связывающим производные и конечные разности , где так же, как и в (37), — условная запись практически постоянных четвёртых разностей. Иногда в качестве величины в формуле берут максимальную четвёртую разность из четвёртых конечных разностей в используемой части таблицы конечных разностей.
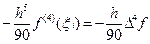
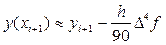
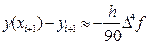
Исходя из точного равенства (38), локальную погрешность получаемого с помощью формулы (39) приближённого значения y_i₊₁ можно приближённо охарактеризовать величиной . Поэтому, сравнивая выражения (38) и (39), можем написать:
или (40)
Далее приравнивая правые части выражений (37) и (40):
» и
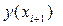
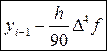
получим:
(41)
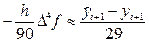
Следовательно, сравнивая выражения (40) и (41), окончательно получаем:
(42)
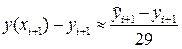
Таким образом, при численном интегрировании начальной задачи (1), (2) методом Милна четвёртого порядка, определяемым формулами (36), (39), на каждом i — м шаге следует вычислять величину
(43)

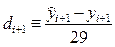
и сравнивать её модуль с величиной e > 0 допустимой шаговой погрешности. Если
½d_i₊₁½ _i+₁) — y М _i+₁ = 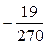(y М _i+₁ — y Б _i+₁). (33)

для предиктор-корректорного метода Адамса четвёртого порядка

(28)

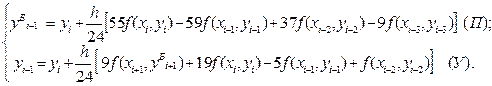
это характеризует метод Милна как несколько более точный при одинаковых вычислительных затратах.

§6. Сведение задачи Коши для систем дифференциальных уравнений первого порядка к задаче Коши для ОДУ первого порядка с использованием векторных обозначений.

Пусть имеется система дифференциальных уравнений первого порядка, разрешённых относительно производных. Задача Коши для такой системы дифференциальных уравнений формулируется в следующем виде:

(45)

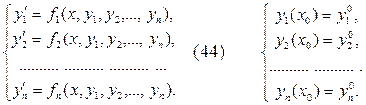
Введём следующие векторныеобозначения:

(46)

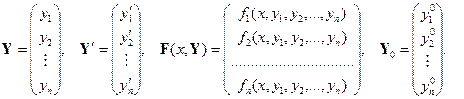
Используя введённые векторные обозначения (46) задача Коши (44), (45) для системы дифференциальных уравнений первого порядка (44) может быть переписана в виде:

, (47)

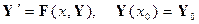
который имеет точно такую же форму, как и рассматриваемая выше задача Коши:

К полученному векторному дифференциальному уравнению (47) применимы все численные методы, изучавшиеся в рамках данной темы, поскольку все рассмотренные методы имеют линейную структуру (т.е. если реализацию какого-либо из рассмотренных методов решения задач Коши представить как действие соответствующего линейного оператора).

При таком подходе скалярными величинами в формулах, определяющих методы, являются только независимая переменная x и расчётный шаг h; всем остальным величинам соответствуют введённые выше векторные величины размерности n.

Следует лишь учесть, что в этом случае при контроле пошаговой или глобальной точности методов вместо модуля нужно использовать норму вектора (например, норму — максимум).

Заключение (план — аннотация лекции №24).

В лекции 24 рассмотрены приближённые методы решения задачи Коши, основанные на интегрировании ДУ и последующей замене подынтегральной функции интерполирующим полиномом соответствующего порядка, данные методы известные в литературе под общим названием многошаговых методов Адамса.

Дан вывод формул экстраполяционного метода Адамса, рассмотрен подход к оценке его точности. Приведён интерполяционный метод Адамса, рассмотрены его частные случаи. Рассмотрены предиктор-корректорные методы Адамса, дан метод осуществления пошагового контроля погрешности вычислений при их применении.

Ещё одним методом прогноза и коррекции, рассмотренным в лекции, является метод Милна, в рамках которого получены две формулы – первая и вторая формулы Милна, которые используются соответственно для предсказания и уточнения (коррекции) искомого решения y(x) задачи Коши. Обсуждается роль первой и второй формулы Милна в процессе формирования решения задачи Коши для ОДУ. Дана оценка шаговой (локальной) погрешности метода Милна.

Сформулирована задача Коши для системы ОДУ первого порядка и дифференциального уравнения второго порядка. Дана схема сведение задачи Коши для систем дифференциальных уравнений первого порядка к виду задачи Коши для обыкновенного дифференциального уравнения первого порядка.

Приведены примеры решения типовых задач.

1. В.М. Вержбицкий. Основы численных методов. – М.: Высшая школа, 2002. – 840 стр.

2. Мастяева И.Н., Семенихина О.Н. Численные методы: Учебное пособие / Московский международный институт эконометрики, информатики, финансов и права. – М.: МЭСИ М., 2003. – 102 стр.

3. Приклонский В.И. Численные методы. Лекционный курс, читаемый в МГУ. Адрес в Интернете ttp://afrodita.phys.msu.ru/download/priklonsky/lections/

Вопросы по теме

«Методы решения начальных задач для обыкновенных дифференциальных уравнений».

1. Основные определения и постановка задачи Коши для ОДУ: Определение ОДУ; уравнение, разрешённое относительно производной; начальная задача; начальные условия; геометрическая интерпретация задачи Коши; Классификация приближенных методов. Теорема об эквивалентности задачи Коши соответствующему интегральному уравнению. Метод последовательных приближений Пикара, его основные свойства.

2. Метод Эйлера. Общая характеристика метода Эйлера в классе численных методов решения задачи Коши. Геометрическая интерпретация метода Эйлера — метод ломаных. Квадратурный подход к выводу метода Эйлера. Модификации метода Эйлера (неявный или обратный метод Эйлера, метод трапеций, Метод Хьюна). Исправленный метод Эйлера, его достоинства и недостатки.

3. Методы решения задачи Коши с помощью формулы Тейлора.Исправленный метод Эйлера, его достоинства и недостатки. Методы Рунге-Куттакак способ модификации исправленного метода Эйлера.Вывод формул семейства методов Рунге-Кутта первого и второго порядка. Геометрическая интерпретация метода Рунге-Кутта второго порядка. Формулы для семейства методов Рунге-Кутта четвёртого порядка. Рекомендации по использованию методов Рунге-Кутта. Свойства сходимости и точности методов Рунге-Кутта.

4. Многошаговые методы Адамса.Экстраполяционный метод Адамса, подходы к оценке его точности. Интерполяционный метод Адамса и его частные случаи. Предиктор-корректорные методы Адамса, осуществление пошагового контроля погрешности вычислений при их применении.

5. Метод Милна. Первая и вторая формула Милна, их роль в процессе формирования решения задачи Коши для ОДУ. Оценка шаговой (локальной) погрешности метода Милна.

6. Разностные аппроксимации задачи Коши. Разностный способ решения задачи Коши. Разностные схемы на основе аппроксимации первой производной. Понятие устойчивости вычислительного процесса и сходимости разностной схемы. Локальные и глобальные ошибки вычислительных процессов решения начальных задач для ОДУ. Связь локальной и глобальной ошибки. Оценка глобальной ошибки численной схемы решения задачи Коши для ОДУ на основе метода Эйлера.

7. Задача Коши для системы ОДУ первого порядка и дифференциальных уравнений высших порядков. Сведение задачи Коши для систем дифференциальных уравнений первого порядка к виду задачи Коши для обыкновенного дифференциального уравнения первого порядка. Сведение дифференциальных уравнений высших порядков к соответствующим задачам Коши для систем дифференциальных уравнений первого порядка.

\|	следующая лекция ==>
Приложение. 1. Ряд Тейлора для функции двух переменныхf (x, y).	\|	ПРИМЕР РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ

Дата добавления: 2015-09-14 ; просмотров: 10285 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

источники:

http://infourok.ru/zadacha-koshi-metod-adamsa-4392928.html

http://helpiks.org/5-23009.html