Решение дифференциальных уравнений первого порядка методом эйлера

Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,у’)=0 или у’=f(x,y). Функция y(x), при подстановке которой уравнение обращается в тождество, называется решением дифференциального уравнения.

Рассмотрим несколько численных методов решения дифференциальных уравнений первого порядка. Описание численных методов приводится для уравнения в виде у’=f(x,y).

Рассмотрим два варианта вывода расчетных формул

Задачи с начальными условиями для систем обыкновенных дифференциальных уравнений

Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений $$ \begin \tag <1>\frac &= f_i (t, u_1, u_2, \ldots, u_n), \quad t > 0\\ \tag <2>u_i(0) &= u_i^0, \quad i = 1, 2, \ldots, m. \end $$

Используя векторные обозначения, задачу (1), (2) можно записать как задачу Коши $$ \begin \tag <3>\frac> &= \pmb(t, \pmb), \quad t > 0, \\ \tag <4>\pmb(0) &= \pmb_0 \end $$ В задаче Коши необходимо по известному решению в точке $ t = 0 $ необходимо найти из уравнения (3) решение при других $ t $.

Численные методы решения задачи Коши

Существует большое количество методов численного решения задачи (3), (4). Вначале рассмотрим простейший явный метод Эйлера и его программную реализацию. Затем будут представлены методы Рунге—Кутта и многошаговые методы.

При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.

Идея численных методов решения задачи (3), (4) состоит из четырех частей:

1. Вводится расчетная сетка по переменной $ t $ (время) из $ N_t + 1 $ точки $ t_0 $, $ t_1 $, $ \ldots $, $ t_ $. Нужно найти значения неизвестной функции $ \pmb $ в узлах сетки $ t_n $. Обозначим через $ \pmb^n $ приближенное значение $ \pmb(t_n) $.

2. Предполагаем, что дифференциальное уравнение выполнено в узлах сетки.

3. Аппроксимируем производные конечными разностями.

4. Формулируем алгоритм, который вычисляет новые значения $ \pmb^ $ на основе предыдущих вычисленных значений $ \pmb^k $, $ k 0 $ при $ \tau\to 0 $.

Явный метод Эйлера

Проиллюстрируем указанные шаги. Для начала введем расчетную сетку. Очень часто сетка является равномерной, т.е. имеет одинаковое расстояние между узлами $ t_n $ и $ t_ $: $$ \omega_\tau = \< t_n = n \tau, n = 0, 1, \ldots, N_t \>. $$

Затем, предполагаем, что уравнение выполнено в узлах сетки, т.е.: $$ \pmb^\prime (t_n) = \pmb(t_n, u(t_n)), \quad t_n \in \omega_\tau. $$

Заменяем производные конечными разностями. С этой целью, нам нужно знать конкретные формулы, как производные могут быть аппроксимированы конечными разностями. Простейший подход заключается в использовании определения производной: $$ \pmb^\prime(t) = \lim_ <\tau \to 0>\frac<\pmb(t+\tau) — \pmb(t)><\tau>. $$

В произвольном узле сетки $ t_n $ это определение можно переписать в виде: $$ \begin \pmb^\prime(t_n) = \lim_ <\tau \to 0>\frac<\pmb(t_n+\tau) — \pmb(t_n)><\tau>. \end $$ Вместо того, чтобы устремлять шаг сетки к нулю, мы можем использовать малый шаг $ \tau $, который даст численное приближение $ u^\prime(t_n) $: $$ \begin \pmb^\prime(t_n) \approx \frac<\pmb^ — \pmb^><\tau>. \end $$ Такая аппроксимация известна как разностная производная вперед и имеет первый порядок по $ \tau $, т.е. $ O(\tau) $. Теперь можно использовать аппроксимацию производной. Таким образом получим явный метод Эйлера: $$ \begin \tag <5>\frac<\pmb^ — \pmb^n> <\tau>= \pmb(t_n, \pmb^). \end $$

Четвертый шаг заключается в получении численного алгоритма. Из (5) следует, что мы должны знать значение $ y^n $ для того, чтобы решить уравнение (5) относительно $ y^ $ и получить формулу для нахождения приближенного значения искомой функции на следующем временном слое $ t_ $: $$ \begin \tag <6>\pmb^ = \pmb^n + \tau \pmb(t_n, \pmb^) \end $$

При условии, что у нас известно начальное значение $ \pmb^0 = \pmb_0 $, мы можем использовать (6) для нахождения решений на последующих временных слоях.

Программная реализация явного метода Эйлера

Выражение (6) может быть как скалярным так и векторным уравнением. И в скалярном и в векторном случае на языке Python его можно реализовать следующим образом

При решении системы (векторный случай), u[n] — одномерный массив numpy длины $ m+1 $ ($ m $ — размерность задачи), а функция F должна возвращать numpy -массив размерности $ m+1 $, t[n] — значение в момент времени $ t_n $.

Таким образом численное решение на отрезке $ [0, T] $ должно быть представлено двумерным массивом, инициализируемым нулями u = np.zeros((N_t+1, m+1)) . Первый индекс соответствует временному слою, а второй компоненте вектора решения на соответствующем временном слое. Использование только одного индекса, u[n] или, что то же самое, u[n, :] , соответствует всем компонентам вектора решения.

Функция euler решения системы уравнений реализована в файле euler.py:

Строка F_ = lambda . требует пояснений. Для пользователя, решающего систему ОДУ, удобно задавать функцию правой части в виде списка компонент. Можно, конечно, требовать чтобы пользователь возвращал из функции массив numpy , но очень легко осуществлять преобразование в самой функции решателе. Чтобы быть уверенным, что результат F будет нужным массивом, который можно использовать в векторных вычислениях, мы вводим новую функцию F_ , которая вызывает пользовательскую функцию F «прогоняет» результат через функцию assaray модуля numpy .

Неявный метод Эйлера

При построении неявного метода Эйлера значение функции $ F $ берется на новом временном слое, т.е. для решении задачи (5) используется следующий метод: $$ \begin \tag <7>\frac<\pmb^ — \pmb^n> <\tau>= \pmb(t_, \pmb^). \end $$

Таким образом для нахождения приближенного значения искомой функции на новом временном слое $ t_ $ нужно решить нелинейное уравнение относительно $ \pmb^ $: $$ \begin \tag <8>\pmb^ — \tau \pmb(t_, \pmb^) — y^n = 0. \end $$

Для решения уравнения (8) можно использовать, например, метод Ньютона.

Программная реализация неявного метода Эйлера

Функция backward_euler решения системы уравнений реализована в файле euler.py:

Отметим, что для нахождения значения u[n+1] используется функция fsolve модуля optimize библиотеки scipy . В качестве начального приближения для решения нелинейного уравнения используется значение искомой функции с предыдущего слоя u[n] .

Методы Рунге—Кутта

Одношаговый метод Рунге—Кутта в общем виде записывается следующим образом: $$ \begin \tag <9>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^s b_i \pmb_i, \end $$ где $$ \begin \tag <10>\pmb_i = \pmb\left( t_n + c_i\tau, \pmb^n + \tau \sum_^s a_\pmb_j \right), \quad i = 1, 2, \ldots, s. \end $$ Формула (9) основана на $ s $ вычислениях функции $ \pmb $ и называется $ s $-стадийной. Если $ a_ = 0 $ при $ j \geq i $ имеем явный метод Рунге—Кутта. Если $ a_ = 0 $ при $ j > i $ и $ a_ \ne 0 $, то $ \pmb_i $ определяется неявно из уравнения $$ \begin \tag <11>\pmb_i = \pmb\left( t_n + c_i\tau, \pmb^n + \tau \sum_^ a_\pmb_j + \tau a_ \pmb_i \right), \quad i = 1, 2, \ldots, s. \end $$ О таком методе Рунге—Кутта говорят как о диагонально-неявном.

Одним из наиболее распространенных является явный метод Рунге-Кутта четвертого порядка: $$ \begin \tag <12>\pmb_1 & = \pmb(t_n, \pmb^n), &\quad \pmb_2 &= \pmb\left( t_n + \frac<\tau><2>, \pmb^n + \tau \frac<\pmb_1> <2>\right),\\ \pmb_3 &= \pmb\left( t_n + \frac<\tau><2>, \pmb^n + \tau \frac<\pmb_2> <2>\right), &\quad \pmb_4 &= \pmb\left( t_n + \tau, \pmb^n + \tau \pmb_3 \right),\\ \frac<\pmb^ -\pmb^n> <\tau>&= \frac<1> <6>(\pmb_1 + 2\pmb_2 + 2\pmb_3 + \pmb_4) & & \end $$

Многошаговые методы

В методах Рунге—Кутта в вычислениях участвуют значения приближенного решения только в двух соседних узлах $ \pmb^n $ и $ \pmb^ $ — один шаг по переменной $ t $. Линейный $ m $-шаговый разностный метод записывается в виде $$ \begin \tag <13>\frac<1> <\tau>\sum_^m a_i \pmb^ = \sum_^ b_i \pmb(t_, \pmb^), \quad n = m-1, m, \ldots \end $$ Вариант численного метода определяется заданием коэффициентов $ a_i $, $ b_i $, $ i = 0, 1, \ldots, m $, причем $ a_0 \ne 0 $. Для начала расчетов по рекуррентной формуле (13) необходимо задать $ m $ начальных значений $ \pmb^0 $, $ \pmb^1 $, $ \dots $, $ \pmb^ $ (например, можно использовать для их вычисления метод Эйлера).

Различные варианты многошаговых методов (методы Адамса) решения задачи с начальными условиями для систем обыкновенных дифференциальных уравнений могут быть получены на основе использования квадратурных формул для правой части равенства $$ \begin \tag <14>\pmb(t_) — \pmb(t_n) = \int_^> \pmb(t, \pmb) dt \end $$

Для получения неявного многошагового метода используем для подынтегральной функции интерполяционную формулу по значениям функции $ \pmb^ = \pmb(t_, \pmb^) $, $ \pmb^n $, $ \dots $, $ \pmb^ $, т.е. $$ \begin \tag <15>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^ b_i \pmb(t_, \pmb^) \end $$

Для интерполяционного метода Адамса (15) наивысший порядок аппроксимации равен $ m+1 $.

Для построения явных многошаговых методов можно использовать процедуру экстраполяции подынтегральной функции в правой части (14). В этом случае приближение осуществляется по значениям $ \pmb^n $, $ \pmb^ $, $ \dots $, $ \pmb^ $ и поэтому $$ \begin \tag <16>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^ b_i \pmb(t_, \pmb^) \end $$

Для экстраполяционного метода Адамса (16) погрешность аппроксимации имеет $ m $-ый порядок.

На основе методов Адамса строятся и схемы предиктор–корректор. На этапе предиктор используется явный метод Адамса, на этапе корректора — аналог неявного метода Адамса. Например, при использовании методов третьего порядка аппроксимации в соответствии с (18) для предсказания решения положим $$ \frac<\pmb^ — \pmb^n> <\tau>= \frac<1> <12>(23 \pmb^ -16\pmb^ + 5\pmb^). $$ Для уточнеия решения (см. (17)) используется схема $$ \frac<\pmb^ — \pmb^n> <\tau>= \frac<1> <24>(9\pmb^ + 19\pmb^ — 5\pmb^ + \pmb^). $$ Аналогично строятся и другие классы многошаговых методов.

Жесткие системы ОДУ

При численном решении задачи Коши для систем обыкновенных дифференциальных уравнений (3), (4) могут возникнуть дополнительные трудности, порожденные жесткостью системы. Локальные особенности поведения решения в точке $ u = w $ передаются линейной системой $$ \begin \frac

= \sum_^ \frac<\partial f_i> <\partial u_j>(t, w) v + \bar(t), \quad t > 0. \end $$
Пусть $ \lambda_i(t) $, $ i = 1, 2, \ldots, m $ — собственные числа матрицы $$ \begin A(t) = \< a_(t) \>, \quad a_(t) = \frac<\partial f_i><\partial u_j>(t, w). \end $$ Система уравнений (3) является жесткой, если число $$ \begin S(t) = \frac <\max_<1 \leq i \leq m>|Re \lambda_i(t)|> <\min_<1 \leq i \leq m>|Re \lambda_i(t)|> \end $$ велико. Это означает, что в решении присутствуют составляющие с сильно различающимися масштабами изменения по переменной $ t $.
Для численное решения жестких задач используются вычислительные алгоритмы, которые имеют повышенный запас устойчивости. Необходимо ориентироваться на использование $ A $-устойчивых или $ A(\alpha) $-устойчивых методов.
Метод называется $ A $-устойчивым, если при решении задачи Коши для системы (3) область его устойчивости содержит угол $$ \begin |\arg(-\mu)| —>
Реферат: Решение дифференциальных уравнений 1 порядка методом Эйлера
1. Постановка задачи 5
2. Обзор существующих методов решения задачи 6 2.1.Метод Рунге-Кутта четвертого порядка для решения
уравнения первого порядка 6
2.2.Задача Коши 6
2.3.Метод Булирша- Штера с использованием
рациональной экстраполяции для системы уравнений 7
2.4 Метод Адамса 8
2.5. Метод Эйлера 9
3. Описание алгоритмов решения задания 13
3.1. Описание переменных 13
3.2. Блок- схема главного модуля 14
3.3. Описание алгоритма главной программы 14
3.4. Блок-схема функции “func” 15
3.5. Описание блок- схемы функции “func” 15
4. Описание программного обеспечения 16
4.1. Описание операционной системы 16
4.2. Описание языка программирования 18
4.3. Описание программы 19
5. Контрольный пример 21
6.Анализ полученных результатов 22
Список литературы 24
Уравнение называется обыкновенным дифференциальным n-го порядка, если F определена и непрерывна в некоторой области и, во всяком случае, зависит от . Его решением является любая функция u( x), которая этому уравнению удовлетворяет при всех x в определённом конечном или бесконечном интервале. Дифференциальное уравнение, разрешенное относительно старшей производной имеет вид
Решением этого уравнения на интервале I=[a,b] называется функция u( x)
Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х₀ , х₁ …, х_n и числа у₀ , не определяя функцию у=F(x), найти такие значения у₁ , у₂ ,…, у_n , что у_i =F(x_i )(i=1,2,…, n) и F(x₀ )=y₀ .
Таким образом, численные методы позволяют вместо нахождения функции y=F(x) (3) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=x_k -x_k-1 называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Метод Эйлера для обыкновенных дифференциальных уравнений используется для решений многих задач естествознания в качестве математической модели. Например задачи электродинамики системы взаимодействующих тел (в модели материальных точек), задачи химической кинетики, электрических цепей. Ряд важных уравнений в частных производных в случаях, допускающих разделение переменных, приводит к задачам для обыкновенных дифференциальных уравнений – это, как правило, краевые задачи (задачи о собственных колебаниях упругих балок и пластин, определение спектра собственных значений энергии частицы в сферически-симметричных полях и многое другое).
1.1. Решить приближенно дифференциальное уравнение вида методом Эйлера
1.2. Составить блок-схему алгоритма для решения данного задания.
1.3. Разработать программу на языке MicrosoftVisualC++
1.4. Протестировать программу на примере y’=2x+y (n=5, [0,1], y0=1)
1.5. Выполнить анализ результатов.
1.6. Оформить пояснительную записку с приложением.
2.Обзор методов решения задачи.
2.1. Метод Рунге-Кутта четвертого порядка для решения уравнения первого порядка.
Идея Рунге-Кута состоит в том, чтобы использовать метод неопределённых коэффициентов. Наиболее употребительным методом Рунге-Кутта решения уравнения первого порядка y’ = F(x,y) (2.1.1) является метод четвертого порядка, в котором вычисления производятся по формуле:
yk+1 = yk +(k1 +2k2 +2k3 +k4 )/6, (2.1.2)
k1 = Fk h = F(xk , yk )h
k2 = F(xk +h/2, yk +k1 /2)h
k3 = F(xk +h/2, yk +k2 /2)h
k4 = F(xk +h, yk +k3 )h,
Рассмотрим задачу Коши для уравнений первого порядка на отрезке [a,b]:
, (2.1.4)
Разобьём промежуток [a,b] на Nчастей . Обозначим , где u(x) –точное решение задачи Коши, и через значения приближенного решения в точках . Существует 2 типа численных схем :
1. явные: ) (2.2.1)
2. неявные: (2.2.2)
Здесь F некоторая функция, связывающая приближения. В явных схемах приближенное значение в точке определяется через некоторое число kуже определённых приближенных значений. В неявных схемах определяется не рекурентным способом, как в явных схемах, а для его определения возникает уравнение, поскольку равенство (2.2.2) представляет из себя именно уравнение на . Явные схемы проще, однако зачастую неявные схемы предпочтительнее.
2.3. Метод Булирша-Штера с использованием рациональной экстраполяции для системы уравнений
Метод Булирша-Штера (Bulirsch-Stoer Method) — это метод решения системы обыкновенных дифференциальных уравнений первого порядка с гладкими правыми частями. Гладкость правых частей является необходимой для работы метода. Если правые части вашей системы не являются гладкими или содержат разрывы, то лучше использовать метод Рунге-Кутта. В случае же гладкой системы метод Булирша-Штера позволяет добиться существенно большей точности, чем метод Рунге-Кутта.
Принцип работы метода
Основной идеей метода является вычисление состояния системы в точке x+h, как результата двух шагов длины h/2, четырех шагов длины h/4, восьми шагов длины h/8 и так далее с последующей экстраполяцией результатов. Метод строит рациональную интерполирующую функцию, которая в точке h/2 проходит через состояние системы после двух таких шагов, в точке h/4 проходит через состояние системы после четырех таких шагов, и т.д., а затем вычисляет значение этой функции в точке h = 0, проводя экстраполяцию.
Гладкость правых частей приводит к тому, что вычисленное при помощи экстраполяции состояние системы оказывается очень близко к действительному, а использование рациональной экстраполяции вместо полиномиальной позволяет ещё больше повысить точность.
Таким образом проводится один шаг метода, после чего принимается решение — следует ли изменять шаг, а если да — то в какую сторону. При этом используется оценка погрешности, которую мы получаем в качестве дополнительного результата при рациональной экстраполяции. Следует отметить, что алгоритм решает автономную систему, т.е. если уравнения системы содержат время, то необходимо ввести время в качестве переменной, производная от которой тождественно равна единице.
Явная схема Адамса.
Рассмотренные выше методы являются явными одношаговыми (для нахождения последующего приближения используется лишь одно предыдущее). Приведённый ниже метод является многошаговым.
Пусть задана задача Коши:
(2.4.1)
Для точного решения (которое нам не известно) выполнено:
(2.4.2)
Предположим, нам известны приближенные значения функции u ( x ) в k точках (стартовые k точек, в частности, можно найти методом Эйлера или методом Рунге-Кутта того или иного порядка), тогда функцию f ( x , u ( x )) в (2.4.2) для приближенного вычисления интеграла можно заменить на интерполяционный полином порядка k -1, построенный поk точкам , интеграл от которого считается явно и представляет собой линейную комбинацию значений cнекоторыми множителями . Таким образом, мы получаем следующую рекуррентную процедуру вычисления приближенных значений функции u ( x ) (являющимся точным решением задачи Коши) в точках :
(2.4.3)
Описанная схема является k — шаговой явной формулой Адамса.
Неявная схема Адамса.
Пусть — интерполяционный полином порядка k , построенный по k +1 значению б одно из которых, именно , мы будем считать неизвестным. Модифицируем (2.4.3), заменив в нём на полином более высокой степени , интеграл от которого выражается в виде линейной комбинации значений с некоторыми новыми коэффициентами :
(2.4.4)
Формула (2.4.4) представляет собой неявную схему Адамса и является уравнением на , которое можно решать методом последовательных приближений. Естественно, что начальное приближение , должно быть разумно выбрано. Для этого удобно объединить явную и неявную схемы Адамса в одну, называемую «методом коррекции». Именно с помощью явной схемы определяется начальное приближение (прогноз), а затем по неявной схеме оно необходимое число раз (обычно один или два) корректируется методом последовательных приближений до достижения заданной точности (коррекция).
Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х₀ , х₁ …, х_n и числа у₀ , не определяя функцию у=F(x), найти такие значения у₁ , у₂ ,…, у_n , что у_i =F(x_i )(i=1,2,…, n) и F(x₀ )=y₀ . (2.5.1)
Таким образом, численные методы позволяют вместо нахождения функции
У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=x_k -x_k-1 называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Рассмотрим дифференциальное уравнение первого порядка (2.5.1)
с начальным условием
Требуется найти решение уравнения (2.5.1) на отрезке [а,b].
Разобьем отрезок [a, b] на n равных частей и получим последовательность х₀ , х₁ , х₂ ,…, х_n , где x_i =x₀ +ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.
В методе Эйлера приближенные значения у(х_i )»y_i вычисляются последовательно по формулам у_i +hf(x_i , y_i ) (i=0,1,2…).
При этом искомая интегральная кривая у=у(х), проходящая через точку М₀ (х₀ , у₀ ), заменяется ломаной М₀ М₁ М₂ … с вершинами М_i (x_i , y_i ) (i=0,1,2,…); каждое звено М_i M_i ₊₁ этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (2.5.1), которая проходит через точку М_i . Если правая часть уравнения (2.5.1) в некотором прямоугольнике R<|x-x₀ |£a, |y-y₀ |£b>удовлетворяет условиям:
|f(x, y₁ )- f(x, y₂ )| £N|y₁ -y₂ | (N=const), (2.5.3)
|df/dx|=|df/dx+f(df/dy)| £ M (M=const),
то имеет место следующая оценка погрешности:
где у(х_n )-значение точного решения уравнения (2.5.1) при х=х_n , а у_n — приближенное значение, полученное на n-ом шаге.
Формула (13) имеет в основном теоретическое применение. На практике иногда оказывается более удобным двойной просчет : сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагомh/2. Погрешность более точного значения у_n * оценивается формулой
Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка.
Модифицированный метод Эйлера
Рассмотрим дифференциальное уравнение (2.5.1) y / =f(x,y) с начальным условием y(x₀ )=y₀ . Разобьем наш участок интегрирования на n равных частей. На малом участинтегральную кривую заменим прямой линией.
Рис.1 Метод Эйлера в графическом видa
Получаем точку N_k / . В этой точке строим следующую касательную:
Из точки М_к проводим прямую с угловым коэффициентом α_к и определяем точку пересечения этой прямой с прямой Х_к1 . Получаем точку М_к / . В качестве у_к+1 принимаем ординату точки М_к / . Тогда:
(2.5.8)-рекурентные формулы метода Эйлера.
Сначала вычисляют вспомогательные значения искомой функции у_к+1/2 в точках х_к+1/2 , затем находят значение правой части уравнения (11) в средней точке y / _k+1/2 =f(x_k _+1/2 , y_k _+1/2 ) и определяют у_к+1 .
Для оценки погрешности в точке х_к проводят вычисления у_к с шагом h, затем с шагом 2h и берут 1/3 разницы этих значений:
где у(х)-точное решение дифференциального уравнения.
Таким образом, методом Эйлера можно решать уравнения любых порядков. Например, чтобы решить уравнение второго порядка y // =f(y / ,y,x) c начальными условиями y / (x₀ )=y / ₀ , y(x₀ )=y₀ , выполняется замена:
3.Описание алгоритмов решения задачи
Название: Решение дифференциальных уравнений 1 порядка методом Эйлера
Раздел: Рефераты по информатике
Тип: реферат Добавлен 10:57:58 05 марта 2011 Похожие работы
Просмотров: 360 Комментариев: 24 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать
Наименование Тип Описание
Входные данные
Xi double Начальное значение (x) интервала вычисления
Xkon double Конечное значение (x) интервала вычисления
n integer Количество шагов
Yi double Начальное значение y
kx double Коэффициент при переменой x
ky double Коэффициент при переменной y
Выходные данные
h double Фиксированное приращение аргумента (x)
res double Расчётное значение уравнение y’=F(x,y) в точке (x)
Промежуточные
i integer Счётчик цикла
Yprom double Промежуточное значение y в точке Xprom
Xprom double Промежуточное значение x при h/2
a double Решение уравнения в точках f(Xprom,Yprom)
f1 double Функция f(x,y)
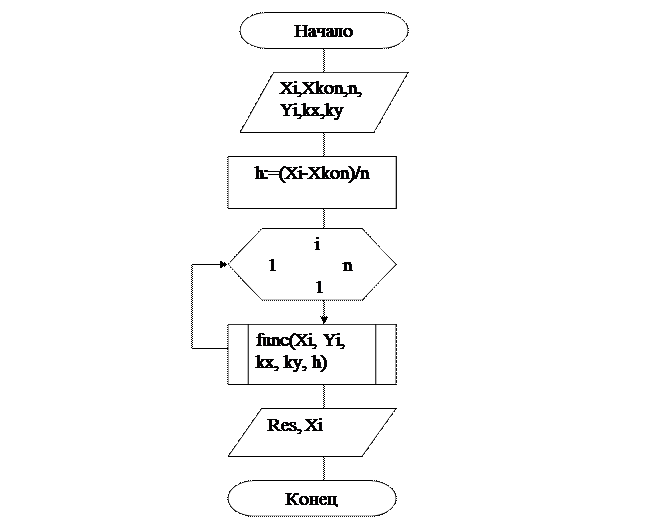
3.2. Блок- схема главного модуля
3.3 Описание алгоритма главной программы.
Вывод результатов на интервале X
3.4 Блок-схема функции “func”.
3.5 Описание блок- схемы функции “func”.
Номер блока Описание
1 Ввод начального и конечного значений интервала вычисления уравнения, количество шагов, начальное значение у, а также коэффициенты при kxи ky.
2 Вычисление фиксированного приращения аргумента х
3 Цикл с шагом 1 и конечным значением не превышающим количество шагов, который высчитывает значение yна определённом интервале
4 Функция для расчёта уравнения вида y’=f(x,y);
Описание
1 Вычисление: функции f1 с подстановкой начальных значений; промежуточных значений Yprom и Xprom, значения aдля вычисления f(Xprom,Yprom) и расчёт результатов функции и переход на следующий шаг.
2 Приращение аргумента xна h
3 Вывод результатов уравнения и интервала
*Реализация алгоритма на языке программирования C++ представлена в приложении .
4.Описание программного обеспечения.
4.1 Описание операционной системы
Основное требование к операционной системе (ОС), предъявляемое поставленной задачей, это наличие ANSI или POSIX совместимого компилятора языка C++.
Для реализации задачи была выбрана последняя клиентская версия операционной системы Microsoft, основанная на ядре NT – MicrosoftWindowsXPProfessional.
Указанная операционная система обладает рядом преимуществ:
· наличие достаточного количество ANSI или POSIX совместимых компиляторов языка C++, разработанных для данной ОС, а именно –
o Microsoft C++ (version 2-6)
· достаточная управляемость, надежность и безопасность;
· широкое распространение основанных на ядре NT операционных систем Microsoft, совместимых по программному обеспечению с WindowsXPProfessional (NT/2000/XP/2003 – client & server);
· высокая скорость работы приложений, разработанных для данной ОС с использованием компиляторов C++.
Исходный код программы может быть откомпилирован и под другой операционной системой, если для таковой имеется ANSI или POSIX совместимый компилятор языка C++.
Программа была протестирована на операционной системе MicrosoftWindowsXPProfessionalSP1.
· Процессор x86 Family 15 Model 2 Stepping 7 GenuineIntel
· Версия BIOS Award Software International, Inc. F4, 06.03.2003
· Аппаратно-зависимый уровень (HAL) Версия = «5.1.2600.1106 (xpsp1.020828-1920)»
· Полный объем физической памяти 256,00 МБ
· Доступно физической памяти 29,97 МБ
· Всего виртуальной памяти 873,69 МБ
· Доступно виртуальной памяти 350,04 МБ
· Файл подкачки 618,21 МБ
4.2 Описание языка программирования
Язык программирования С++
С++ — это универсальный язык программирования, задуманный так, чтобы сделать программирование более приятным для серьезного программиста. За исключением второстепенных деталей С++ является надмножеством языка программирования C. Помимо возможностей, которые дает C, С++ предоставляет гибкие и эффективные средства определения новых типов. Используя определения новых типов, точно отвечающих концепциям приложения, программист может разделять разрабатываемую программу на лег ко поддающиеся контролю части. Такой метод построения программ часто называют абстракцией данных. Информация о типах содержится в некоторых объектах типов, определенных пользователем. Такие объекты просты и надежны в использовании в тех ситуациях, когда их тип нельзя установить на стадии компиляции. Программирование с применением таких объектов часто называют объектно-ориентированным. При правильном использовании этот метод дает более короткие, проще понимаемые и легче контролируемые программы.
В С++ нет типов данных высокого уровня и нет первичных операций высокого уровня. В нем нет, например, матричного типа с операцией обращения или типа строка с операцией конкатенации. Если пользователю понадобятся подобные типы, их можно определить в самом языке. По сути дела, основное, чем занимается программирование на С++ — это определение универсальных и специально-прикладных типов. Хорошо разработанный тип, определяемый пользователем, отличается от встроенного типа только способом определения, но не способом использования.
Реализация С++ очень легко переносима. Однако есть полные основания использовать С++ в среде, где имеется гораздо более существенная поддержка. Такие средства, как динамическая загрузка, пошаговая трансляция и база данных определений типов могут с пользой применяться без воздействия на язык.
Типы и средства сокрытия данных в С++ опираются на проводимый во время компиляции анализ программ с целью предотвращения случайного искажения данных. Они не обеспечивают секретности или защиты от умышленного нарушения правил. Однако эти средства можно использовать без ограничений, что не приводит к дополнительным расходам времени на выполнение или пространства памяти.
Компилятор MicrosoftC++ и среда разработки MicrosoftVisualStudio
В качестве компилятора для разработки приложения был выбран MicrosoftC++ по следующим причинам:
· практически полная совместимость со стандартом ANSIC++;
· наличие удобной среды разработки MicrosoftVisualStudio;
· наличие отличной документации;
· высокая скорость работы результирующих приложений;
· совместимость разработанных приложений с большим количеством широко распространенных операционных систем;
· достаточная скорость компиляции.
4.3 Описание программы
Разработанное приложение поставляется в виде 2-ух файлов:
1. methodEulera.cpp – исходный код программы на языке C++;
2. methodEulera.exe – исполняемый файл.
Для выполнения исполняемого файла необходима одна из ниже перечисленных операционных систем:
· Microsoft Windows 3.11+Win32s;
· Microsoft Windows 95/98/Me;
· MicrosoftWindowsNT/2000/XP/2003 – клиентская или серверная версия.
Программа не требует предварительной установки и может быть сразу же запущена на выполнение.
Исходный код приложения может быть откомпилирован в любом ANSI или POSIX совместимом компиляторе С++ для получения выполнимой программы. Для успешной компиляции требуется наличие стандартной библиотеки «iostream».
5. Контрольный пример
Данный метод протестирован на контрольном примере и реализован с помощью языка программирования С++.
В результате вычислений контрольного примера вида y’=2 x+ y с интервалом [0,1],
количеством шагов равному 5 и начальным условием у равным 1 , с помощью программы, получились следующие результаты:
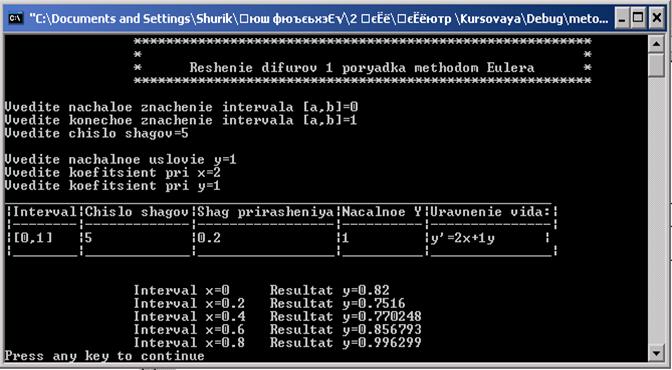
Рис. 2. Экран с результатами выполнения программы.
Как видно, при вычислении программа на первом шаге берёт начальные значения для вычисления, а на последующих берёт значения полученные с предыдущих шагов. Можно сделать вывод, что точность вычисления данного метода зависит от количества выбранных шагов: чем больше шагов, тем меньше фиксированное приращение , а следовательно она более точно вычисляет значение всего интервала.
По работе программы стало видно, что с её использованием намного упростилась работа пользователя. Пользователь просто вводит интервал на котором должен вычисляться пример, количество шагов и начальное значения и программа выдаёт уже готовое решение данного примера.
6.Анализ полученных результатов.
По результатам программы можно составить таблицу сравнения результатов полученных при использовании программы и результатов, полученных ручным способом:
Ручной способ вычисления Программный способ вычисления
Х Y X Y
0 0,82 0 0,82
0,2 0,75 0,2 0,7516
0,4 0,77 0,4 0,770248
0,6 0,85 0,6 0,856793
0,8 0,99 0,8 0,996299
Из приведенного сравнения можно сделать вывод, что один результат отличается от другого тем, что в примере, решенном программным способом ответ вычисляется с наибольшей точностью, чем при ручном способе. Это может быть связано с тем, что в ручном способе результат округляется для удобства вычисления примера.
Решение дифференциальных уравнений методом Эйлера можно также отобразить в графическом виде:
Рис.3.Графическое изображение решения примера y’=2x+y
Как видно из рис.3 графиком решения уравнения является кривая , форма которой зависит от количества разбиений интервала.
По результатам выполненной работы можно сделать вывод, что решение дифференциальных уравнений методом Эйлера является методом вычисления со средней точностью и точность вычисления данного метода зависит от количества разбиений интервала интегрирования. При сравнении результатов решенными разными способами можно сказать, что данный метод был верно реализован на языке программирования MicrosoftVisualC++. Полученные результаты сходятся с небольшой погрешностью.
1. Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения), Н.С. Бахвалов. Главная редакция физико- математической литературы изд-ва «Наука», М., 1975г.
2. Методы, теории обыкновенных дифференциальных уравнений. Н.И. Гаврилов . Государственное издательство «Высшая школа» Москва-1962г.
3. В.В.Пак., Ю.Л. Носенко. Высшая математика: Учебник.- Д.: Сталкер, 1997г.
4. Б. П. Демидович, И. А. Марон Основы вычислительной математике. – М., 1966
5. Загускин В. Л. – Справочник по численным методам решения уравнений. – М.: ФИЗМАТГИЗ, 1960. – 216 с.
6. Либерти, Джесс.
Освой самостоятельно С++ за 21 день, 4-е издание.:Пер с англ.-М.: Издательский дом «Вильямс», 2003.-832с.
7. П.Нортон, П.Иао «Программирование на С++ в среде Windows» («Диалектика» Киев 2003г.)
8. Янг М. Microsoft Visual C++ — М.:ЭНТРОП, 2000.
9. Марченко А.И., Марченко Л.А. – Программирование в среде
Turbo Pascal 7.0 – К.: ВЕК+, М.: Бином Универсал, 1998. – 496 с.
10. Высшая математика: Справ. материалы: Книга для учащихся .- М.:

источники:
http://slemeshevsky.github.io/num-mmf/ode/html/._ode-FlatUI001.html
http://www.bestreferat.ru/referat-274013.html