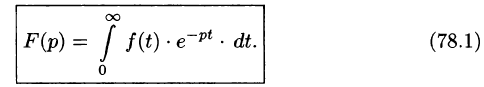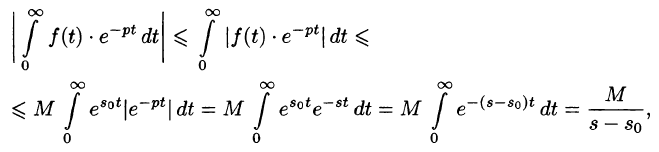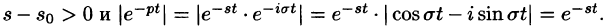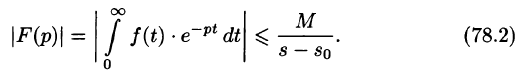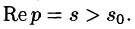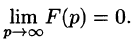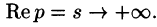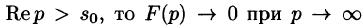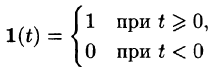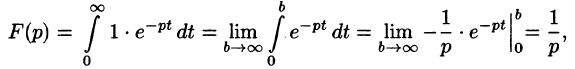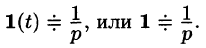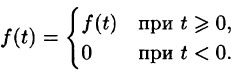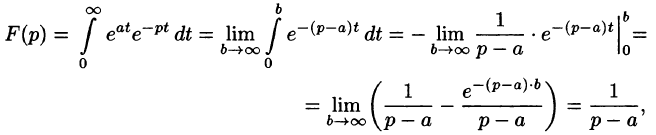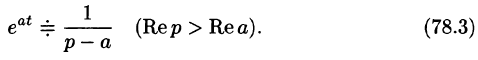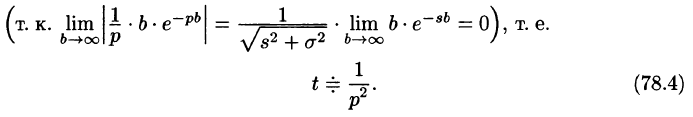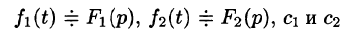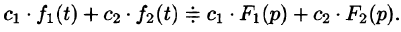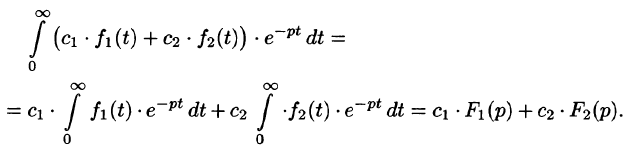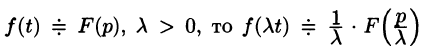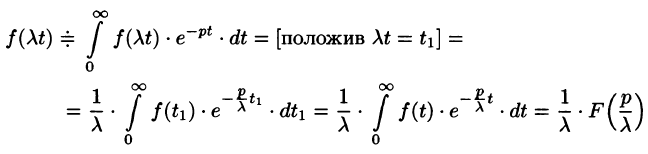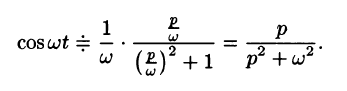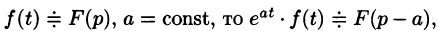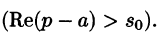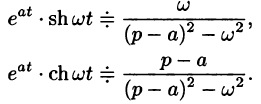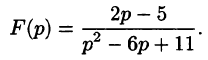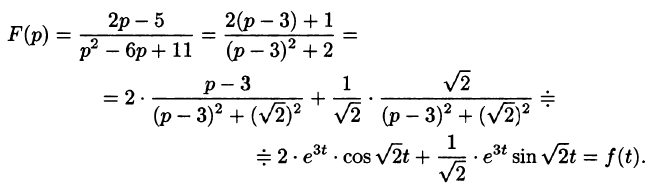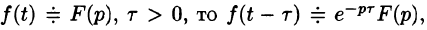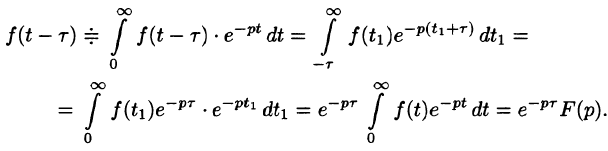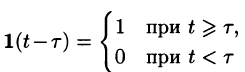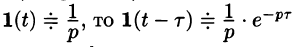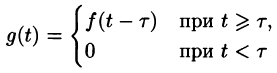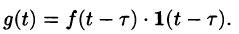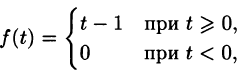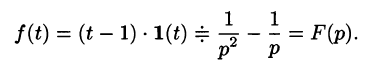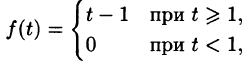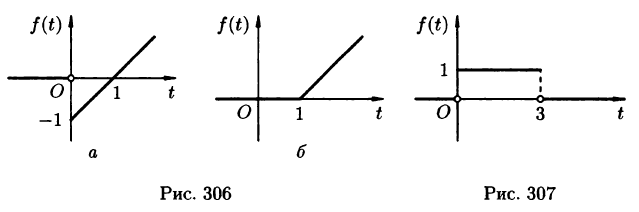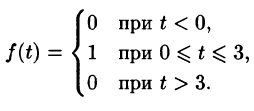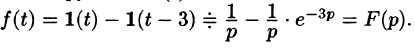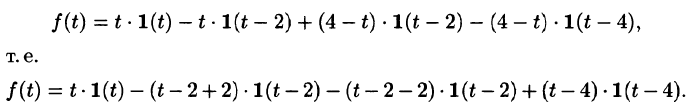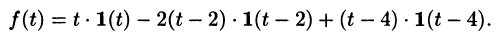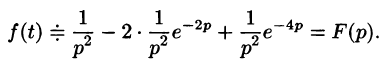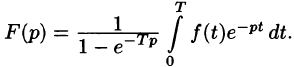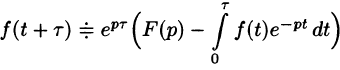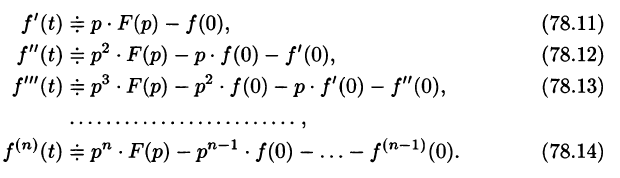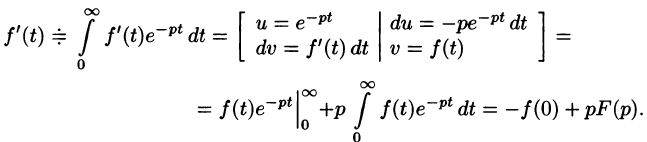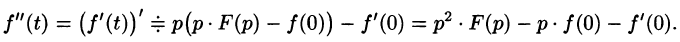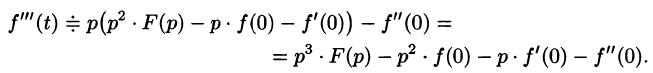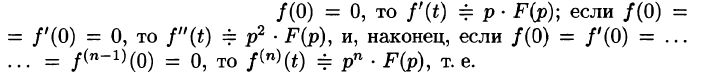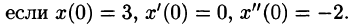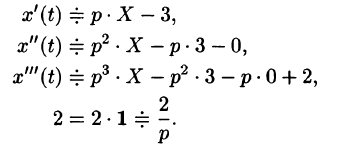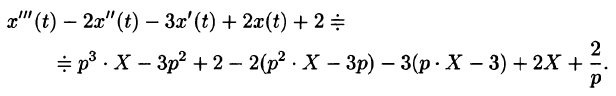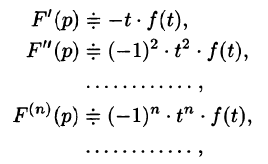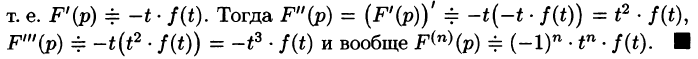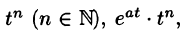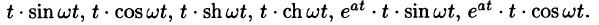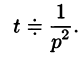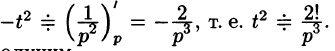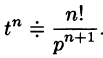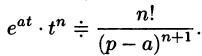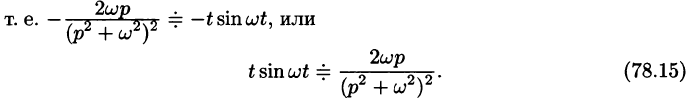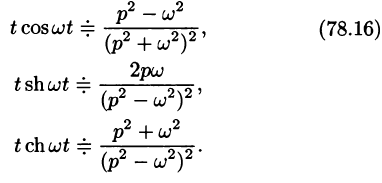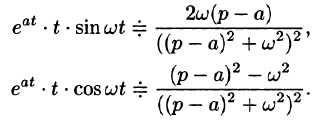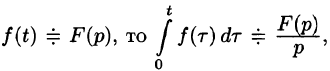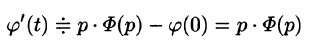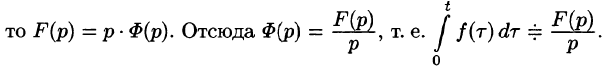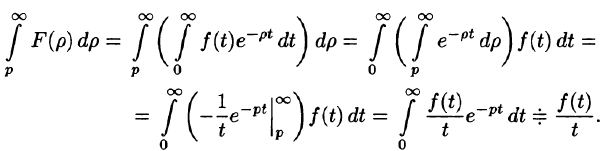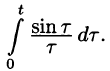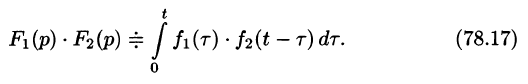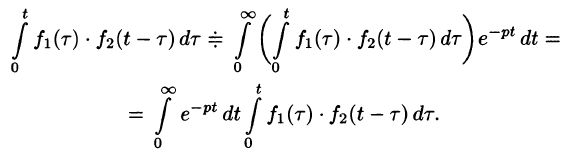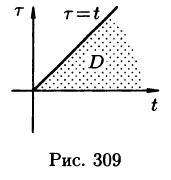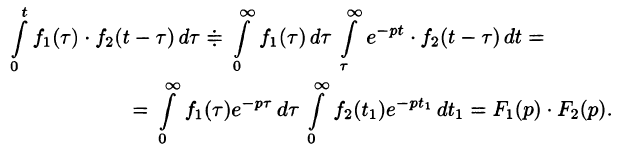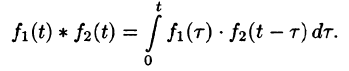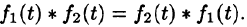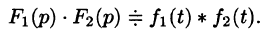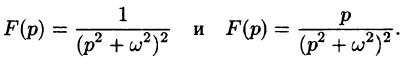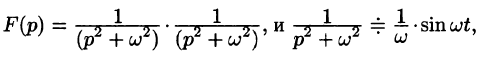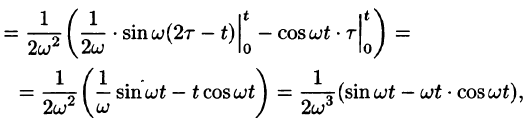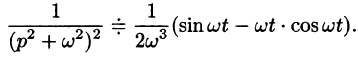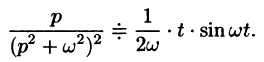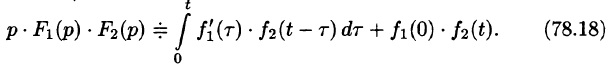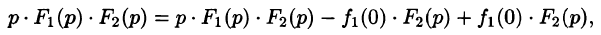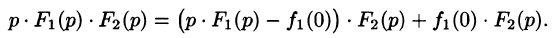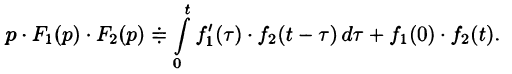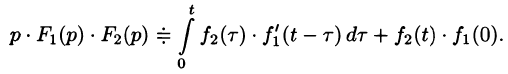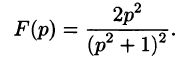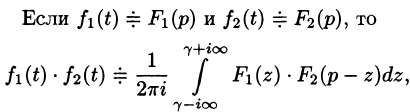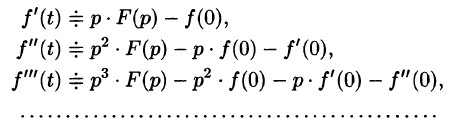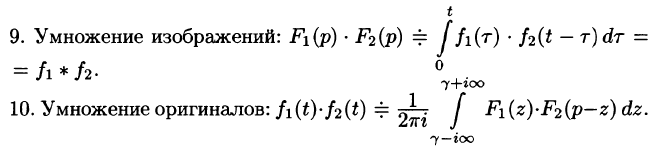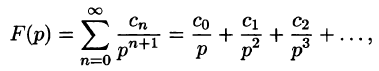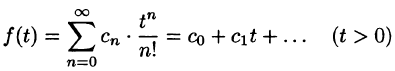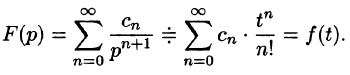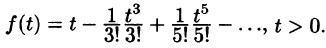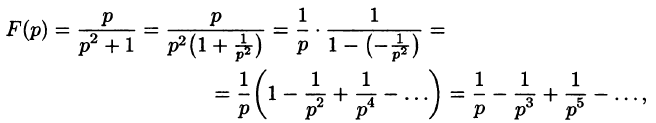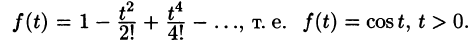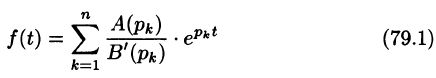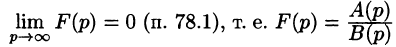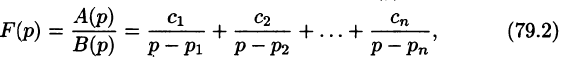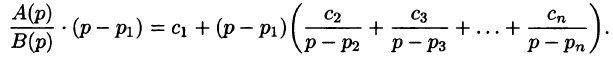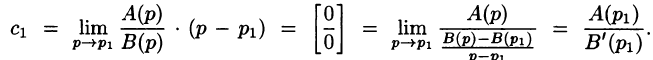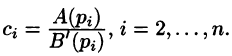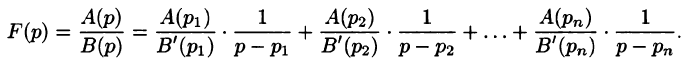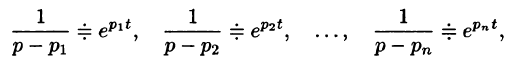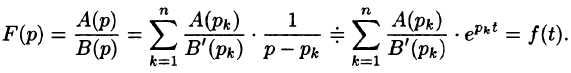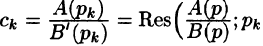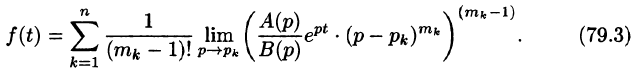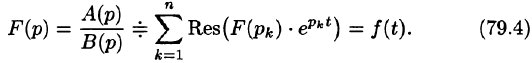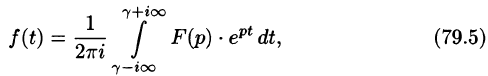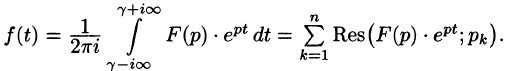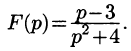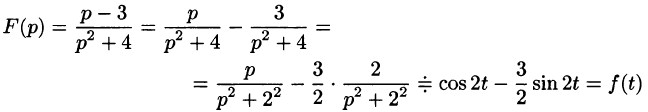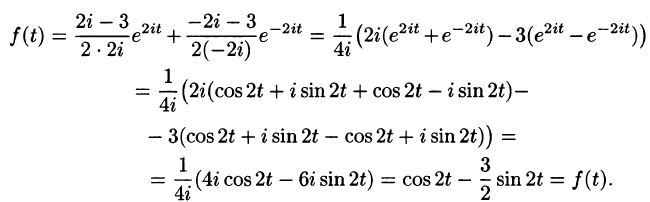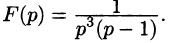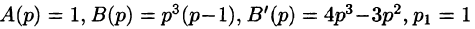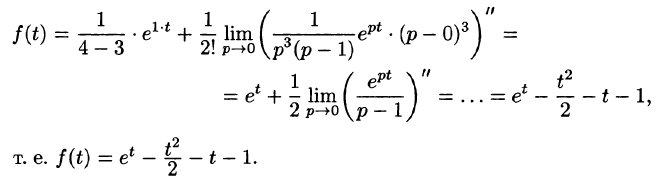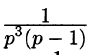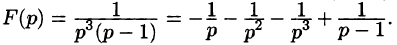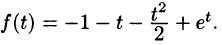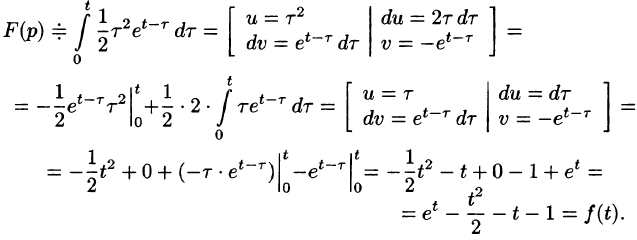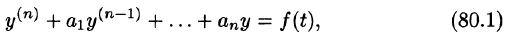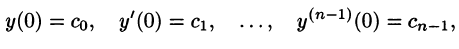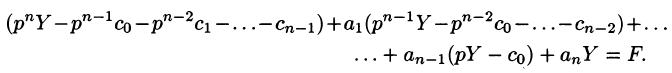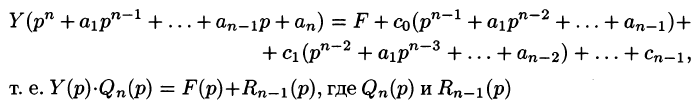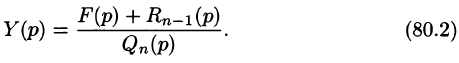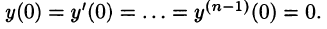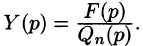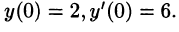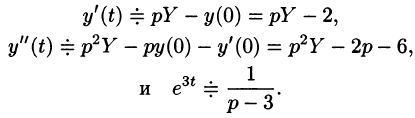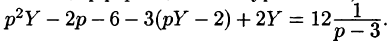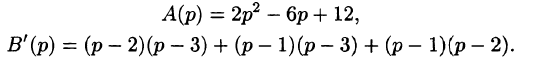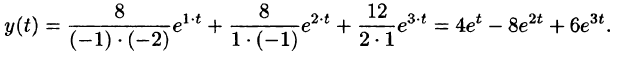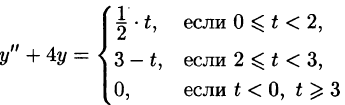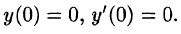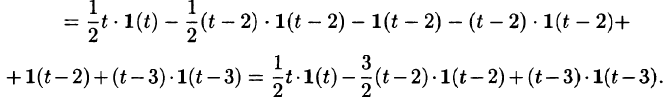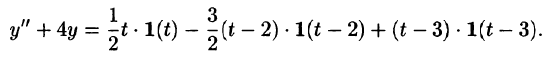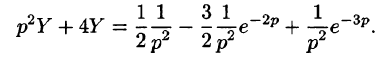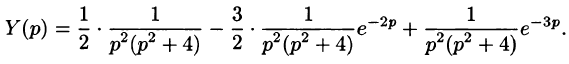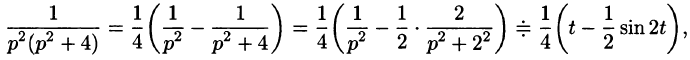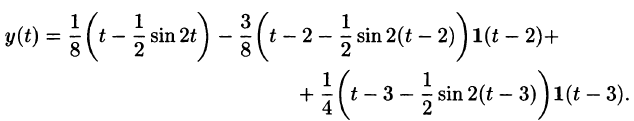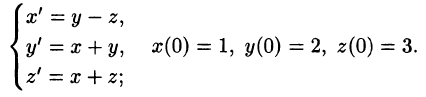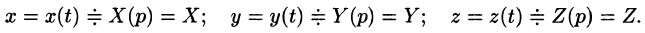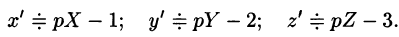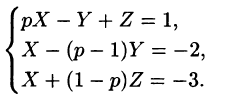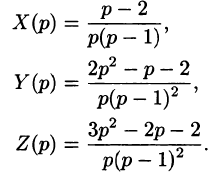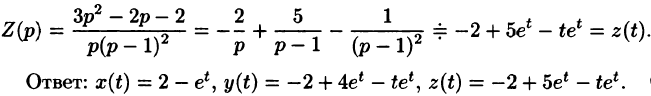Примеры решений задач по операционному исчислению (преобразованию Лапласа)
Операционное (символическое) исчисление – это один из методов математического анализа, позволяющий в некоторых случаях свести исследование и решение дифференциальных, псевдодифференциальных, интегральных уравнений, к более простым алгебраическим задачам.
Изучая преобразование Лапласа, мы вводим оригинал функции $f(t)$ и ее изображение $F(p)$, находимое по формуле:
$$F(p) = \int_0^\infty f(t) e^<-pt>dt$$
Для быстроты и удобства решения задач составлена таблица изображений и оригиналов, которая, наряду с теоремами (линейности, подобия, смещения, запаздывания), свойствами и правилами дифференцирования и интегрирования изображения/оригинала, постоянно используется в решении примеров.
В этом разделе вы найдете готовые задания разного типа: восстановление оригинала или изображения функции, нахождение свертки функций, решение ДУ, систем ДУ или интегральных уравнений с помощью преобразования Лапласа и т.д.
Как найти изображение функции
Задача 1. Найти изображение данного оригинала, или оригинала, удовлетворяющего данному уравнению
Задача 2. Пользуясь определением, найти изображение функции $f(t)=3^t$.
Задача 3. Найти изображение функции: $\int_0^t \cos \tau \cdot e^<-3\tau>d\tau. $
Задача 4. Найти изображение оригинала $f(x)$ двумя способами:
1) Вычислив интеграл $F(p) = \int_0^\infty f(x) e^<-px>dx$;
2) Воспользовавшись таблице изображений и свойствами преобразования Лапласа.
Оригинал задается формулой (курсочно-линейная функция, см. файл).
Как найти оригинал функции
Задача 5. Найти оригинал изображения $F(p)$, где
Задача 6. Найти оригинал изображения
Задача 7. Найти оригинал для функции с помощью вычетов
Как решить ДУ (систему ДУ) операционным методом
Задача 8. Найти частное решение дифференциального уравнения с заданными начальными условиями операторным методом
Задача 9. Найти решение задачи Коши методами операционного исчисления
Задача 10. Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.
Задача 11. Методом операционного исчисления найти решение задачи Коши для ДУ 3-го порядка
Задача 12. Решите задачу Коши для системы дифференциальных уравнений с помощью преобразования Лапласа.
Задача 13. C помощью формулы Дюамеля найти решение уравнения
Задача 14. Решить систему ДУ с помощью преобразования Лапласа
Как решить интегральное уравнение
Задача 15. Методом операционного исчисления найти решение интегрального уравнения
$$ y(t)=\cos t +\int_0^t (t-\tau)^2 y(\tau)d \tau. $$
Задача 16. Решить интегральное уравнение
$$ \int_0^t ch (\tau) x(t-\tau)d \tau = t. $$
Как найти свертку функций
Задача 17. Найти свертку функций $f(t)=1$ и $\phi(t)=\sin 5t$.
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей , оформление производится в Word, срок от 1 дня.
Символьное решение линейных дифференциальных уравнений и систем методом преобразований Лапласа c применением SymPy
Реализация алгоритмов на языке Python с использованием символьных вычислений очень удобна при решении задач математического моделирования объектов, заданных дифференциальными уравнениями. Для решения таких уравнений широко используются преобразования Лапласа, которые, говоря упрощенно, позволяют свести задачу к решению простейших алгебраических уравнений.
В данной публикации предлагаю рассмотреть функции прямого и обратного преобразования Лапласа из библиотеки SymPy, которые позволяют использовать метод Лапласа для решения дифференциальных уравнений и систем средствами Python.
Сам метод Лапласа и его преимущества при решении линейных дифференциальных уравнений и систем широко освещены в литературе, например в популярном издании [1]. В книге метод Лапласа приведен для реализации в лицензионных программных пакетах Mathematica, Maple и MATLAB (что подразумевает приобретение учебным заведением этого ПО) на выбранных автором отдельных примерах.
Попробуем сегодня рассмотреть не отдельный пример решения учебной задачи средствами Python, а общий метод решения линейных дифференциальных уравнений и систем с использованием функций прямого и обратного преобразования Лапласа. При этом сохраним обучающий момент: левая часть линейного дифференциального уравнения с условиями Коши будет формироваться самим студентом, а рутинная часть задачи, состоящая в прямом преобразовании Лапласа правой части уравнения, будет выполняться при помощи функции laplace_transform().
История об авторстве преобразований Лапласа
Преобразования Лапласа (изображения по Лапласу) имеют интересную историю. Впервые интеграл в определении преобразования Лапласа появился в одной из работ Л. Эйлера. Однако в математике общепринято называть методику или теорему именем того математика, который открыл ее после Эйлера. В противном случае существовало бы несколько сотен различных теорем Эйлера.
В данном случае следующим после Эйлера был французский математик Пьер Симон де Лаплас (Pierre Simon de Laplace (1749-1827)). Именно он использовал такие интегралы в своей работе по теории вероятностей. Самим Лапласом не применялись так называемые «операционные методы» для нахождения решений дифференциальных уравнений, основанные на преобразованиях Лапласа (изображениях по Лапласу). Эти методы в действительности были обнаружены и популяризировались инженерами-практиками, особенно английским инженером-электриком Оливером Хевисайдом (1850-1925). Задолго до того, как была строго доказана справедливость этих методов, операционное исчисление успешно и широко применялось, хотя его законность ставилось в значительной мере под сомнение даже в начале XX столетия, и по этой теме велись весьма ожесточенные дебаты.
Функции прямого и обратного преобразования Лапласа
Эта функция возвращает (F, a, cond), где F(s) есть преобразование Лапласа функции f(t), a Текст программы
Время на обратное визуальное преобразование Лапласа: 2.68 s
Обратное преобразование Лапласа часто используется при синтезе САУ, где Python может заменить дорогостоящих программных “монстров” типа MathCAD, поэтому приведенное использование обратного преобразования имеет практическое значение.
Преобразование Лапласа от производных высших порядков для решения задачи Коши
Если a и b — константы, то
для всех s, таких, что существуют оба преобразования Лапласа (изображения по Лапласу) функций f(t) и q(t).
Проверим линейность прямого и обратного преобразований Лапласа с помощью ранее рассмотренных функций laplace_transform() и inverse_laplace_transform(). Для этого в качестве примера примем f(t)=sin(3t), q(t)=cos(7t), a=5, b=7 и используем следующую программу.
(7*s**3 + 15*s**2 + 63*s + 735)/((s**2 + 9)*(s**2 + 49))
(7*s**3 + 15*s**2 + 63*s + 735)/((s**2 + 9)*(s**2 + 49))
True
5*sin(3*t) + 7*cos(7*t)
5*sin(3*t) + 7*cos(7*t)
Приведенный код также демонстрирует однозначность обратного преобразования Лапласа.
Если предположить, что удовлетворяет условиям первой теоремы, то из этой теоремы будет следовать, что:
Повторение этого вычисления дает
После конечного числа таких шагов мы получаем следующее обобщение первой теоремы:
Применяя соотношение (3), содержащее преобразованные по Лапласу производные искомой функции с начальными условиями, к уравнению (1), можно получить его решение по методу, специально разработанному на нашей кафедре при активной поддержке Scorobey для библиотеки SymPy.
Метод решения линейных дифференциальных уравнений и систем уравнений, основанный на преобразованиях Лапласа, с использованием библиотеки SymPy
где — приведенное начальное положение массы,
— приведенная начальная скорость массы.
Упрощённая физическая модель, заданная уравнением (4) при ненулевых начальных условиях [1]:
Система, состоящая из материальной точки заданной массы, закрепленной на пружине, удовлетворяет задаче Коши (задаче с начальными условиями). Материальная точка заданной массы первоначально находится в покое в положении ее равновесия.
Для решения этого и других линейных дифференциальных уравнений методом преобразований Лапласа удобно пользоваться следующей системой, полученной из соотношений (3):
Последовательность решения средствами SymPy следующая:
- загружаем необходимые модули и явно определяем символьные переменные:
указываем версию библиотеки sympy, чтобы учесть ее особенности. Для этого нужно ввести такие строки:
по физическому смыслу задачи переменная времени определяется для области, включающей ноль и положительные числа. Задаём начальные условия и функцию в правой части уравнения (4) с её последующим преобразование по Лапласу. Для начальных условий необходимо использовать функцию Rational, поскольку использование десятичного округления приводит к ошибке.
пользуясь (5), переписываем преобразованные по Лапласу производные, входящие в левую часть уравнения (4), формируя из них левую часть этого уравнения, и сравниваем результат с правой его частью:
решаем полученное алгебраическое уравнение относительно преобразования X(s) и выполняем обратное преобразование Лапласа:
осуществляем переход из работы в библиотеке SymPyв библиотеку NumPy:
строим график обычным для Python методом:
Получаем:
Версия библиотеки sympy – 1.3
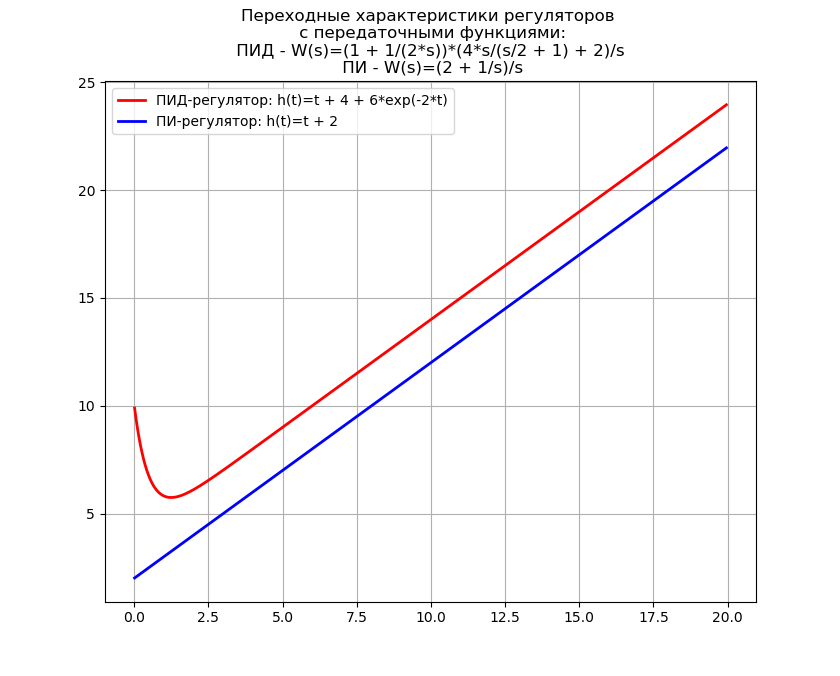
Получен график периодической функции, дающей положение материальной точки заданной массы. Метод преобразования Лапласа с использованием библиотеки SymPy дает решение не только без потребности сначала найти общее решение однородного уравнения и частное решение первоначального неоднородного дифференциального уравнения, но и без потребности использования метода элементарных дробей и таблиц Лапласа.
При этом учебное значение метода решения сохраняется за счёт необходимости использования системы (5) и перехода в NumPy для исследования решения более производительными методами.
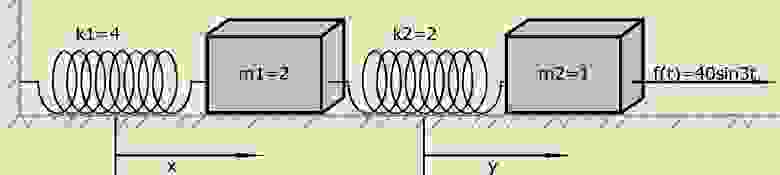
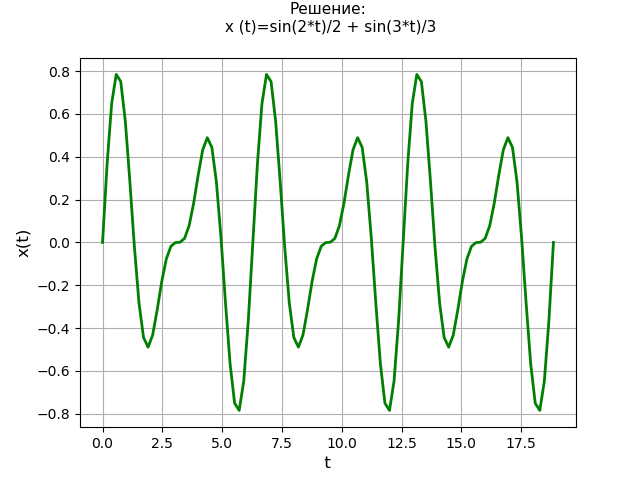
Для дальнейшей демонстрации метода решим систему дифференциальных уравнений:
с начальными условиями
Упрощённая физическая модель, заданная системой уравнений (6) при нулевых начальных условиях:
Таким образом, сила f(t) внезапно прилагается ко второй материальной точке заданной массы в момент времени t = 0, когда система находится в покое в ее положении равновесия.
Решение системы уравнений идентично ранее рассмотренному решению дифференциального уравнения (4), поэтому привожу текст программы без пояснений.
Для ненулевых начальных условий текст программы и график функций примет вид:
Рассмотрим решение линейного дифференциального уравнения четвёртого порядка с нулевыми начальными условиями:
Решим линейное дифференциальное уравнение четвёртого порядка:
с начальными условиями ,
,
.
Функции для решения ОДУ
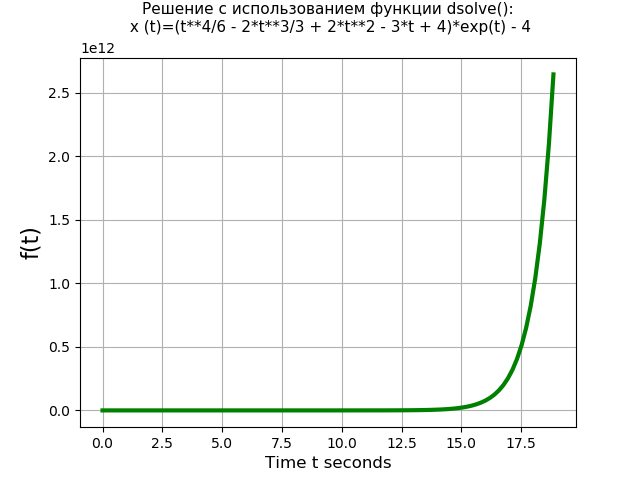
Для имеющих аналитическое решение ОДУ и систем ОДУ применяется функция dsolve():
sympy.solvers.ode.dsolve(eq, func=None, hint=’default’, simplify=True, ics=None, xi=None, eta=None, x0=0, n=6, **kwargs)
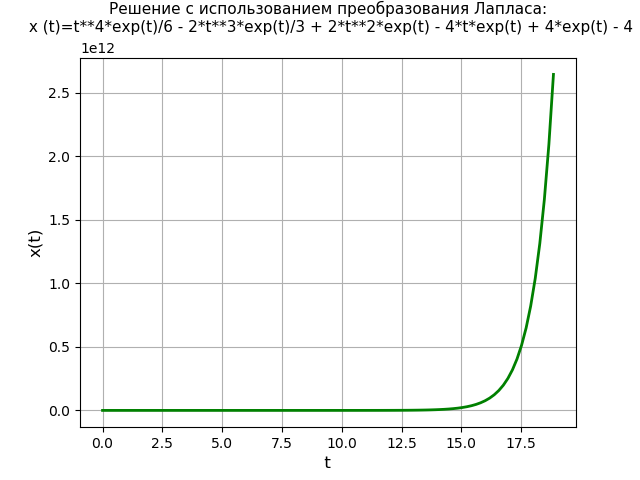
Давайте сравним производительность функции dsolve() с методом Лапласа. Для примера возьмём следующее дифференциальное уравнение четвёртой степени с нулевыми начальными условиями:
Время решения уравнения с использованием функции dsolve(): 1.437 s
Время решения уравнения с использованием преобразования Лапласа: 3.274 s
Итак, функция dsolve() (1.437 s) решает уравнение четвёртого порядка быстрее, чем выполняется решение по методу преобразований Лапласа (3.274 s) более чем в два раза. Однако при этом следует отметить, что функция dsolve() не решает системы дифференциальных уравнений второго порядка, например, при решении системы (6) с использованием функция dsolve() возникает ошибка:
Данная ошибка означает, что решение системы дифференциальных уравнений с помощью функции dsolve() не может быть представлено символьно. Тогда как при помощи преобразований Лапласа мы получили символьное представление решения, и это доказывает эффективность предложенного метода.
Для того чтобы найти необходимый метод решения дифференциальных уравнений с помощью функции dsolve(), нужно использовать classify_ode(eq, f(x)), например:
Eq(f(x), C1*sin(x) + C2*cos(x))
(‘nth_linear_constant_coeff_homogeneous’, ‘2nd_power_series_ordinary’)
(‘separable’, ‘1st_exact’, ‘almost_linear’, ‘1st_power_series’, ‘lie_group’, ‘separable_Integral’, ‘1st_exact_Integral’, ‘almost_linear_Integral’)
[Eq(f(x), -acos((C1 + Integral(0, x))*exp(-Integral(-tan(x), x))) + 2*pi), Eq(f(x), acos((C1 + Integral(0,x))*exp(-Integral(-tan(x), x))))]
Таким образом, для уравнения eq=Eq(f(x).diff(x,x)+f(x),0) работает любой метод из первого списка:
Для уравнения eq = sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x) работает любой метод из второго списка:
separable, 1st_exact, almost_linear,
1st_power_series, lie_group, separable_Integral,
1st_exact_Integral, almost_linear_Integral
Чтобы использовать выбранный метод, запись функции dsolve() примет вид, к примеру:
Вывод:
Данная статья ставила своей целью показать, как использовать средства библиотек SciPy и NumPy на примере решения систем линейных ОДУ операторным методом. Таким образом, были рассмотрены методы символьного решения линейных дифференциальных уравнений и систем уравнений методом Лапласа. Проведен анализ производительности этого метода и методов, реализованных в функции dsolve().
- Дифференциальные уравнения и краевые задачи: моделирование и вычисление с помощью Mathematica, Maple и MATLAB. 3-е издание.: Пер. с англ. — М.: ООО «И.Д. Вильяме», 2008. — 1104 с.: ил. — Парал. тит. англ.
- Использование обратного преобразования Лапласа для анализа динамических звеньев систем управления
Операционное исчисление с примерами решения и образцами выполнения
Операционное исчисление играет важную роль при решении прикладных задач, особенно в современной автоматике и телемеханике.
Операционное исчисление — один из методов математического анализа, позволяющий в ряде случаев сводить исследование дифференциальных и некоторых типов интегральных операторов и решение уравнений, содержащих эти операторы, к рассмотрению более простых алгебраических задач.
Методы операционного исчисления предполагают реализацию следующей условной схемы решения задачи.
- От искомых функций переходят к некоторым другим функциям — их изображениям.
- Над изображениями производят операции, соответствующие заданным операциям над самими функциями.
- Получив некоторый результат при действиях над изображениями, возвращаются к самим функциям.
В качестве преобразования, позволяющего перейти от функции к их изображениям, будем применять так называемое преобразование Лапласа.
Преобразование Лапласа
Оригиналы и их изображения:
Основными первоначальными понятиями операционного исчисления являются понятия функции-оригинала и функции-изображения.
Пусть f(t) — действительная функция действительного переменного t (под t будем понимать время или координату).
Функция f(t) называется оригиналом, если она удовлетворяет следующим условиям:
- f(t)— кусочно-непрерывная при
т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси t таких точек лишь конечное число.
- Существуют такие числа
что для всех t выполняется неравенство
, т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции. Число
называется показателем роста f(t).
Условия 1-3 выполняются для большинства функций, описывающих различные физические процессы.
Первое условие означает, что процесс начинается с некоторого момента времени; удобнее считать, что в момент t = 0. Третьему условию удовлетворяют ограниченные функции (для них можно положить 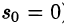
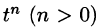
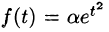
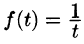
Замечание:
Функция f(t) может быть и комплексной функцией действительно переменного, т. е. иметь вид 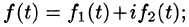
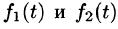
Изображением оригинала f(t) называется функция F(p) комплексного переменного 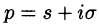
Операцию перехода от оригинала f(t) к изображению F(p) называют преобразованием Лапласа. Соответствие между оригиналом f(t) и изображением F(p) записывается в виде 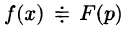
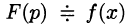
Теорема:
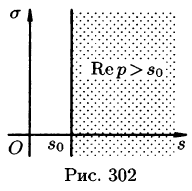
Существование изображения. Для всякого оригинала f(t) изображение F(p) существует (определено) в полуплоскости 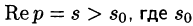
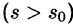
Докажем первую часть теоремы. Пусть 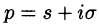
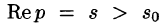
Учитывая, что 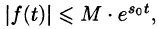
Отсюда вытекает абсолютная сходимость интеграла (78.1), т. е. изображение F(p) существует и однозначно в полуплоскости
Следствие:
Необходимый признак существования изображения. Если функция F(p) является изображением функции f(t) , то
Это утверждение непосредственно вытекает из неравенства (78.2), когда
Так как F(p) — аналитическая функция в полуплоскости
по любому направлению. Отсюда, в частности, следует, что функции 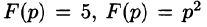
Отметим, что из аналитичности функции F(p) следует, что все ее особые точки должны лежать левее прямой 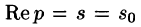
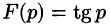
Теорема:
О единственности оригинала. Если функция F(p) служит изображением двух оригиналов 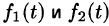
(Примем без доказательства.)
Пример:
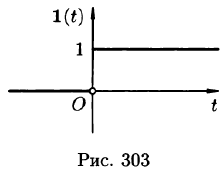
Найти изображение единичной функции Хевисайда
Решение:
По формуле (78.1) при 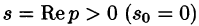
т. e. 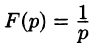
В дальнейшем функцию-оригинал будем кратко записывать в виде f(t) , подразумевал, что
Пример:
Найти изображение функции 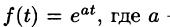
Решение:
Данная функция является оригиналом. По формуле (78.1) имеем
если Re(p — a) > 0. Таким образом,
Пример:
Найти изображение функции f(t) = t.
Решение:
В этом случае преобразование Лапласа имеет вид
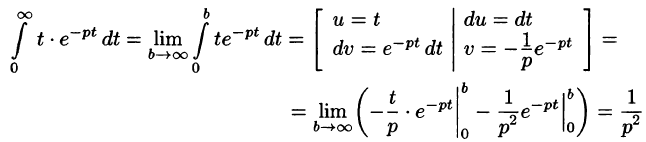
Замечание:
Функция 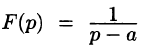
Свойства преобразования Лапласа
Находить изображения, пользуясь только определением изображения, не всегда просто и удобно. Свойства преобразования Лапласа существенно облегчают задачу нахождения изображений для большого числа разнообразных функций, а также задачу отыскания оригиналов по их изображениям.
Линейность
Линейной комбинации оригиналов соответствует такая же линейная комбинация изображений, т. е. если
— постоянные числа, то
Используя свойства интеграла, находим
Пример:
Найти изображения функций 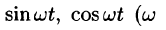
Решение:
Пользуясь свойством линейности, формулой (78.3), находим:
Аналогично получаем формулу
Далее, 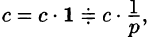
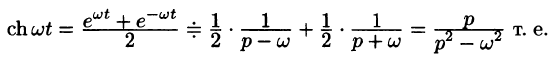
Аналогично получаем формулу
т.е. умножение аргумента оригинала на положительное число 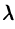
По формуле (78.1) имеем
(так как безразлично, какой буквой обозначена переменная интегрирования).
Например, пусть 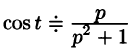
Смещение (затухание)
т. е. умножение оригинала на функцию 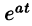
В силу формулы (78.1) имеем
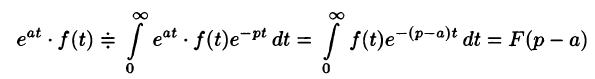
Благодаря этому свойству можно расширить таблицу соответствия между оригиналами и их изображениями:
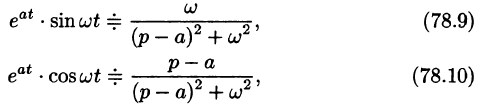
Пример:
Найти оригинал по его изображению
Решение:
Преобразуем данную дробь так, чтобы можно было воспользоваться свойством смещения:
(См. формулы (78.9), (78.10) и свойство линейности.)
Запаздывание
т. е. запаздывание оригинала на положительную величину 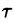
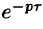
Положив 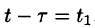
Поясним термин «запаздывание». Графики функции f(t) и 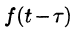
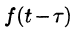
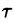
Рис. 304
Рис. 305
вправо (см. рис. 304). Следовательно, функции f(t) и 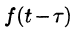
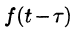
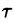
Свойство запаздывания удобно применять при отыскании изображения функций, которые на разных участках задаются различными аналитическими выражениями; функций, описывающих импульсные процессы.
называется обобщенной единично ной функцией (см. рис 305).
можно записать так:
Пример:
Найти изображение f(t) = t — 1.
Решение:
Для того чтобы быть оригиналом, функция f(t) должна удовлетворять условиям 1-3 (см. п. 78.1). В этом смысле исходную задачу можно понимать двояко.
Если понимать функцию f(t) как
т. е. 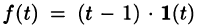
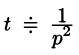
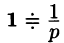
Если же понимать функцию f(t) как
т. е. 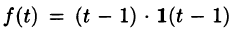
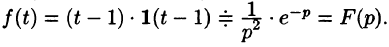
Пример:
Найти изображение функции
Решение:
Данная функция описывает единичный импульс (см. рис. 307), который можно рассматривать как разность двух оригиналов: единичной функции 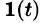
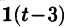
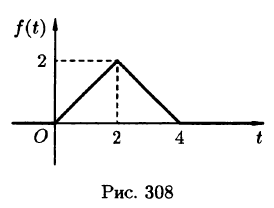
Пример:
Найти изображение функции

Решение:
Функция-оригинал изображена на рис. 308. Запишем ее одним аналитическим выражением, используя функции Хевисайда 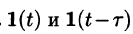
Раскроем скобки и приведем подобные слагаемые:
Изображение функции f(t) будет равно
Замечания:
1.Изображение периодического оригинала с периодом, равным Т,
есть
применяется значительно реже.
Дифференцирование оригинала
Если 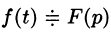
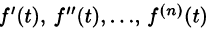
По определению изображения находим
Итак, 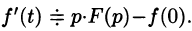
Аналогично найдем изображение третьей производной f»‘(t):
Применяя формулу (78.11) (п — 1) раз, получим формулу (78.14).
Замечание. Формулы (78.11)-(78.14) просто выглядят при нулевых начальных условиях: если
т. е. дифференцированию оригинала соответствует умножение его изображения на р.
Рассмотренное свойство дифференцирования оригинала вместе со свойством линейности широко используется при решении линейных дифференциальных уравнений.
Пример:
Найти изображение выражения
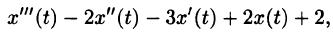
Решение:
Пусть 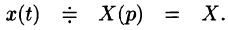
Дифференцирование изображения
Если 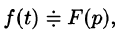
т. е. дифференцированию изображения соответствует умножение его оригинала на (-t).
Согласно теореме 78.1 существования изображения, F(p) является аналитической функцией в полуплоскости 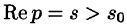
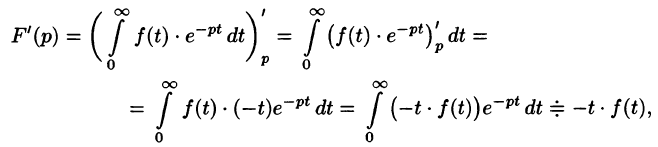
Пример:
Найти изображения функций
Решение:
Так как 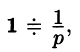
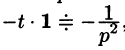
Продолжая дифференцирование, получим
С учетом свойства смещения получаем
Согласно формуле (78.5), 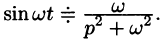
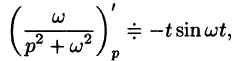
Аналогично, используя формулы (78.6), (78.7) и (78.8), находим
С учетом свойства смещения и формул (78.15) и (78.16), получаем
Интегрирование оригинала
т. е. интегрированию оригинала от 0 до t соответствует деление его изображения на р.
Функция 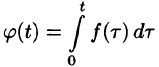
Пусть 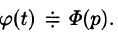
(так как 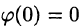
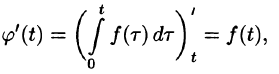
Интегрирование изображения
Если 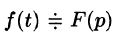
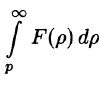
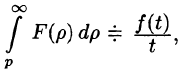
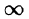
Используя формулу (78.1) и изменяя порядок интегрирования (обоснование законности этой операции опускаем), получаем
Пример:
Найти изображение функции 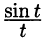
Решение:
т. е. 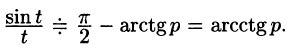
Умножение изображений
Если 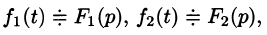
Можно показать, что функция 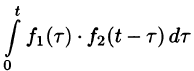
Используя преобразование Лапласа (78.1), можно записать
Область D интегрирования полученного двукратного интеграла определяется условиями 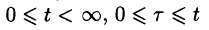
Изменяя порядок интегрирования и полагая 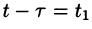
Интеграл в правой части формулы (78.17) называется сверткой функции 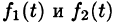
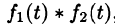
Можно убедиться (положив 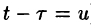
Умножение изображений соответствует свертыванию их оригиналов, т. е.
Пример:
Найти оригинал функций
Решение:
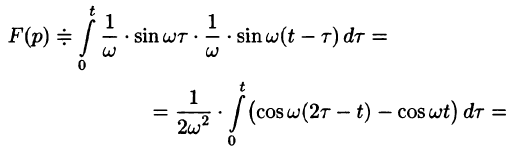
Следствие:
Если 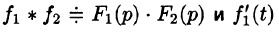
Запишем произведение 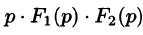
Первое слагаемое в правой части есть произведение изображений, соответствующих оригиналам 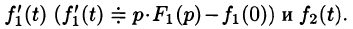
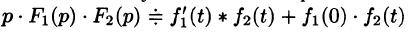
Формула (78.18) называется формулой Дюамеля. На основании свойства переместительности свертки формулу Дюамеля можно записать в виде
Формулу Дюамеля можно применять для определения оригиналов по известным изображениям.
Пример:
Найти оригинал, соответствующий изображению
Решение:
то на основании формулы Дюамеля (78.18) имеем
Умножение оригиналов
где путь интегрирования — вертикальная прямая 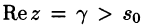
Рассмотренные свойства преобразования Лапласа представляют собой основные правила (аппарат) операционного исчисления. Для удобства пользования перечислим эти свойства.
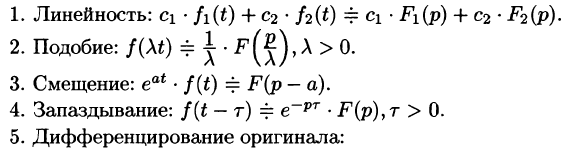
6. Дифференцирование изображения
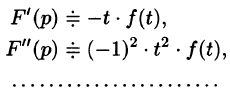
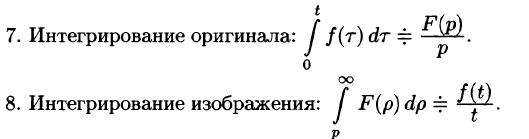
Таблица оригиналов и изображений
Составим краткую таблицу, устанавливающую соответствие между некоторыми оригиналами (часто встречающимися на практике) и их изображениями. Достаточно полная таблица оригиналов и изображений, позволяющая по заданному оригиналу находить изображение и наоборот, есть, в частности, в книге «Справочник по операционному исчислению» (авторы В. А. Диткин и П. И. Кузнецов).


Обратное преобразование Лапласа
Теоремы разложения:
Рассмотрим две теоремы, называемые теоремами разложения, позволяющие по заданному изображению F(p) находить соответствующий ему оригинал f(t).
Теорема:
Если функция F(p) в окрестности точки 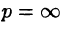
является оригиналом, имеющим изображение F(p), т. е.
Примем эту теорему без доказательства.
Пример:
Найти оригинал f(t), если
Решение:
Следовательно, на основании теоремы 79.1
Запишем лорановское разложение функции 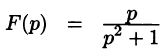
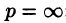
где 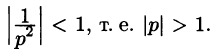
Теорема:
Если 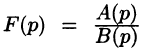
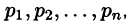
является оригиналом, имеющим изображение F(p).
Отметим, что дробь 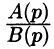
не может быть изображением.
Разложим правильную рациональную дробь 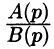
где 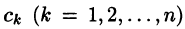
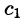
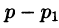
Переходя в этом равенстве к пределу при 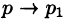
Итак, 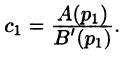
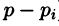
Подставляя найденные значения 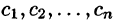
Так как по формуле (78.3)
то на основании свойства линейности имеем
Замечание:
Легко заметить, что коэффициенты 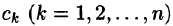
Можно показать, что если 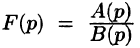
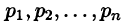
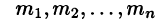
Теорему 79.2 можно сформулировать следующим образом:
Теорема:
Если изображение 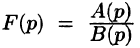
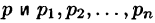
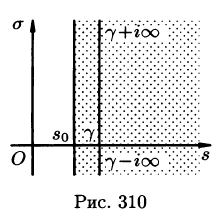
Формула Римана-Меллина
Общий способ определения оригинала по изображению дает обратное преобразование Лапласа (формула обращения Римана-Меллина), имеющее вид
где интеграл берется вдоль любой прямой 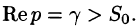
При определенных условиях интеграл (79.5) вычисляется по формуле
Замечание:
На практике отыскание функции-оригинала обычно проводят по следующему плану: прежде всего следует по таблице оригиналов и изображений попытаться отыскать для заданного изображения F(p) соответствующий ему оригинал; второй путь состоит в том, что функцию F(p) стараются представить в виде суммы простейших рациональных дробей, а затем, пользуясь свойством линейности, найти оригинал; наконец, использовать теоремы разложения, свойство умножения изображений, формулу обращения и т.д.
Пример:
Найти оригинал по его изображению
Решение:
Проще всего поступить так:
(использовали свойство линейности и формулы (78.5) и (78.6)).
Если же использовать теорему 79.2 разложения, то будем иметь:
корни знаменателя 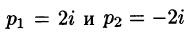
Пример:
Найти функцию-оригинал, если ее изображение
задано как
Решение:
— простой корень знаменателя, 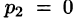
Приведем другой способ нахождения f(t). Разобьем дробь
на сумму простейших дробей:
Приведем третий способ нахождения f(t). Представим F(p) как
произведение 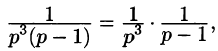
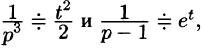
Операционный метод решения линейных дифференциальных уравнений и их систем
Пусть требуется найти частное решение линейного дифференциального уравнения с постоянными коэффициентами
удовлетворяющее начальным условиям
где 
Будем считать, что искомая функция y(t) вместе с ее рассматриваемыми производными и функция f(t) являются оригиналами.
Пусть 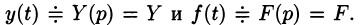
Полученное уравнение называют операторным (или уравнением в изображениях). Разрешим его относительно Y:
— алгебраические многочлены от p степени п и п-1 соответственно. Из последнего уравнения находим
Полученное равенство называют операторным решением дифференциального уравнения (80.1). Оно имеет более простой вид, если все начальные условия равны нулю, т. е.
В этом случае
Находя оригинал y(t), соответствующий найденному изображению (80.2), получаем, в силу теоремы единственности, частное решение дифференциального уравнения (80.1).
Замечание:
Полученное решение y(t) во многих случаях оказывается справедливым при всех значениях t (а не только при 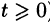
Пример:
Решить операционным методом дифференциальное уравнение 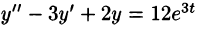
Решение:
Пусть 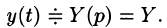
Подставляя эти выражения в дифференциальное уравнение, получаем операторное уравнение:
Отсюда 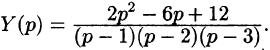
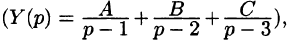
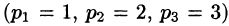
Пример:
Найти решение уравнения
при условии
Решение:
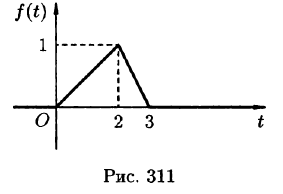
График данной функции имеет вид, изображенный на рисунке 311.
С помощью единичной функции правую часть данного дифференциального уравнения можно записать одним аналитическим выражением:
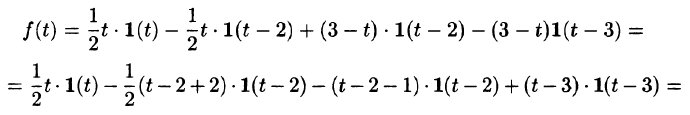
Таким образом, имеем
Операторное уравнение, при нулевых начальных условиях имеет вид
то по теореме запаздывания находим:
Аналогично применяется операционный метод для решения систем линейных дифференциальных уравнений с постоянными коэффициентами.
Покажем это на конкретном примере.
Пример:
Решить систему дифференциальных уравнений
Решение:
Система операторных уравнений принимает вид
Решая эту систему алгебраических уравнений, находим:
Переходя от изображений к оригиналам, получаем искомые решения:
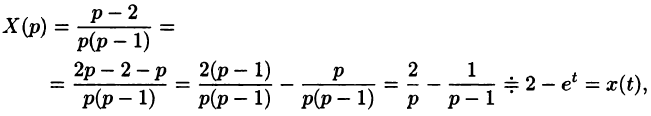
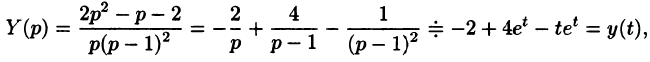
С помощью операционного исчисления можно также находить решения линейных дифференциальных уравнений с переменными коэффициентами, уравнений в частных производных, уравнений в конечных разностях (разностных уравнений); производить суммирование рядов; вычислять интегралы. При этом решение этих и других задач значительно упрощается.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://habr.com/ru/post/426041/
http://lfirmal.com/operacionnoe-ischislenie/







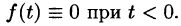
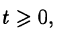 т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси t таких точек лишь конечное число.
т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси t таких точек лишь конечное число.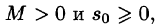 что для всех t выполняется неравенство
что для всех t выполняется неравенство 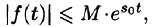 , т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции. Число
, т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции. Число 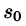 называется показателем роста f(t).
называется показателем роста f(t).