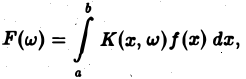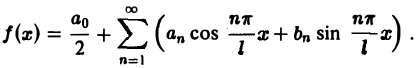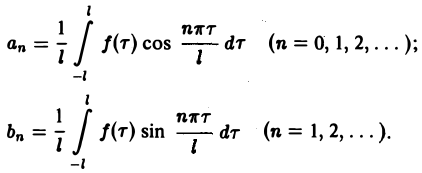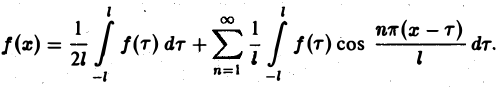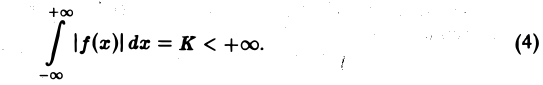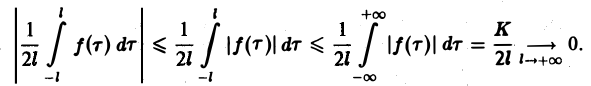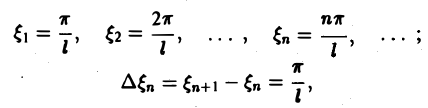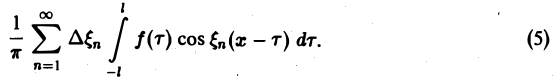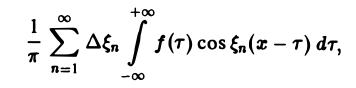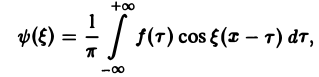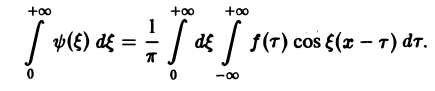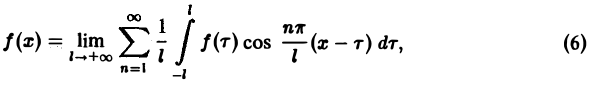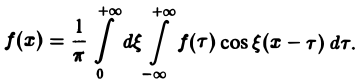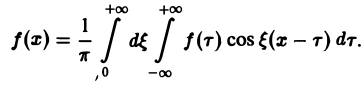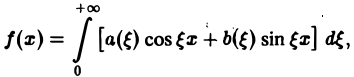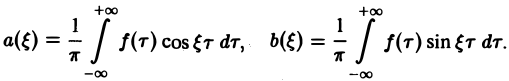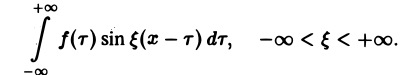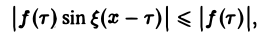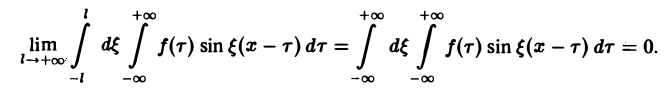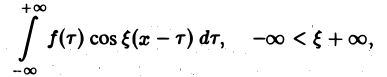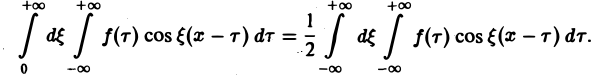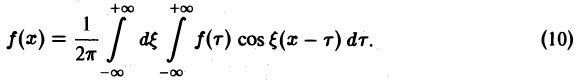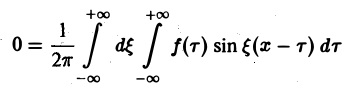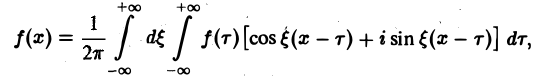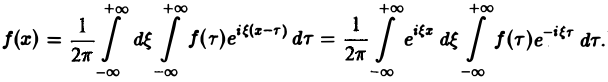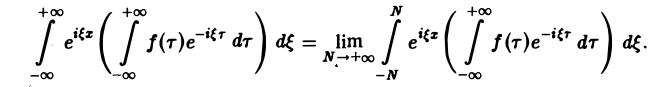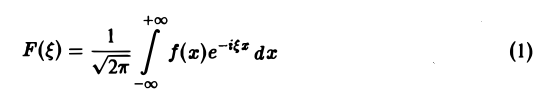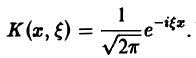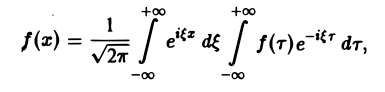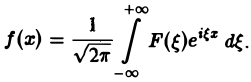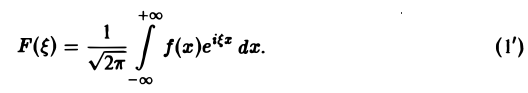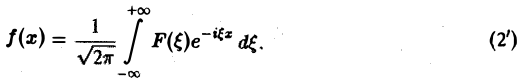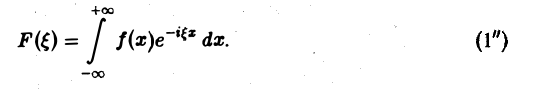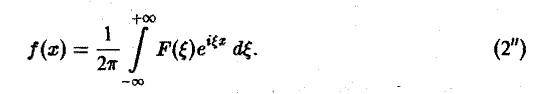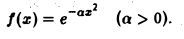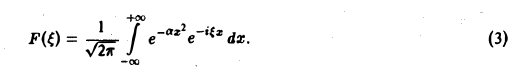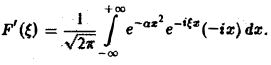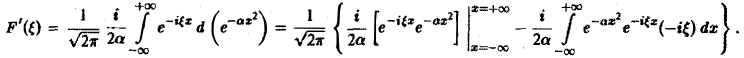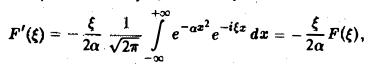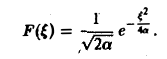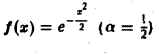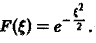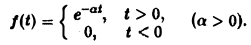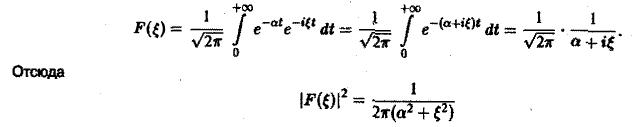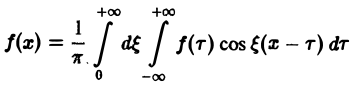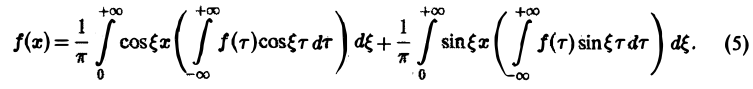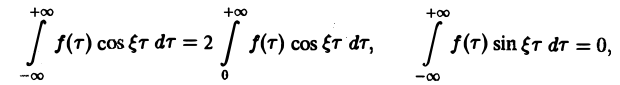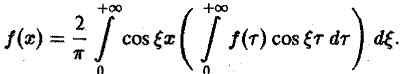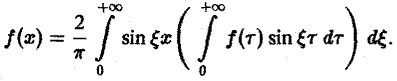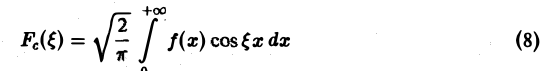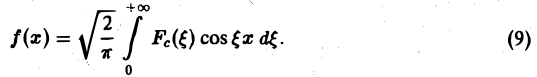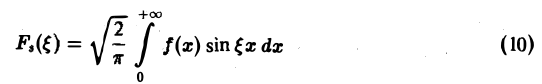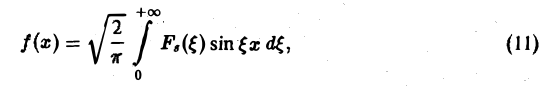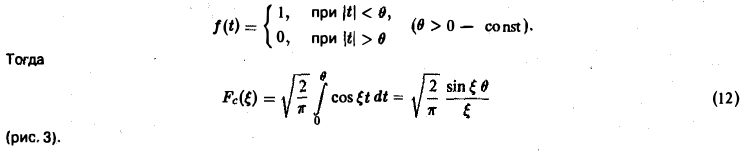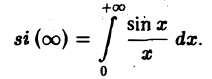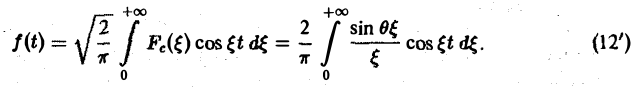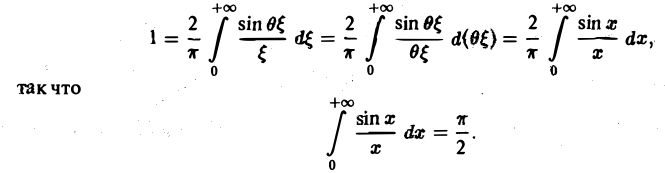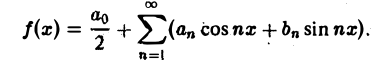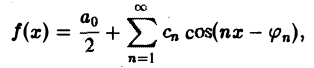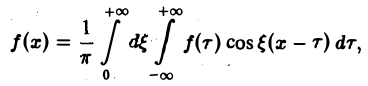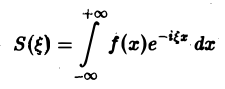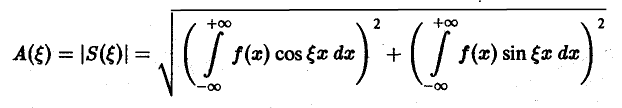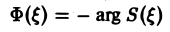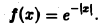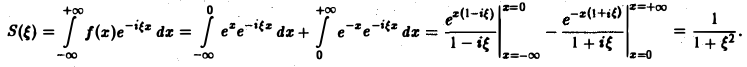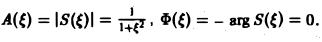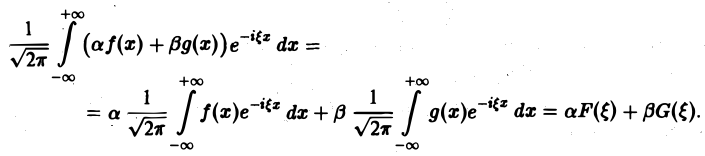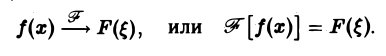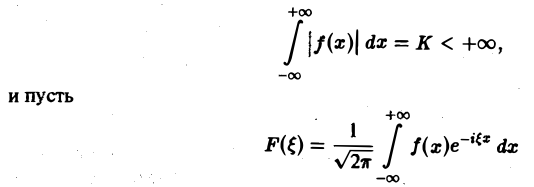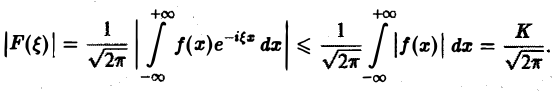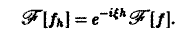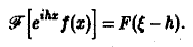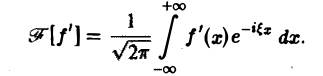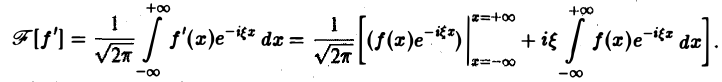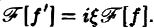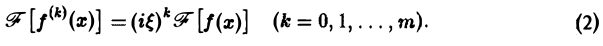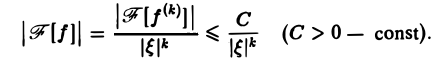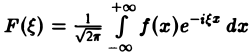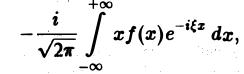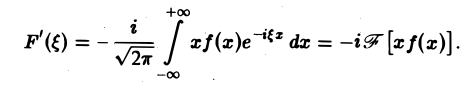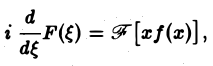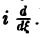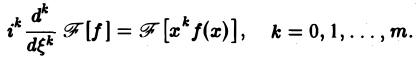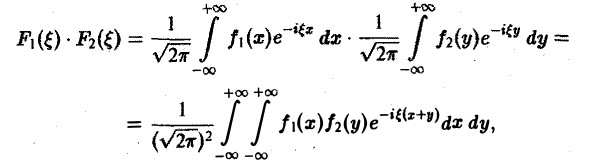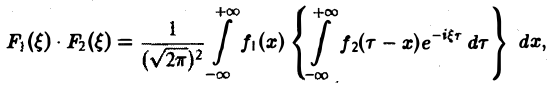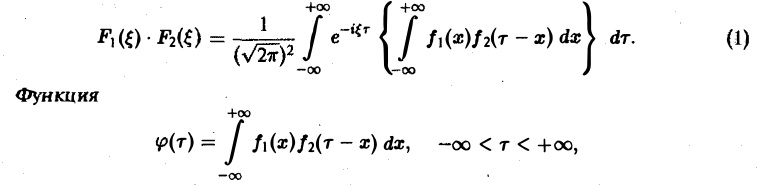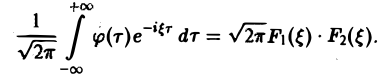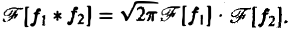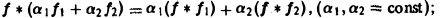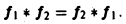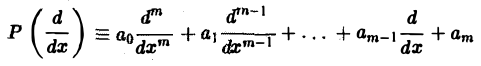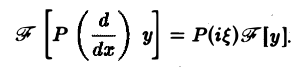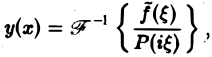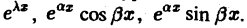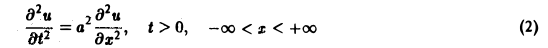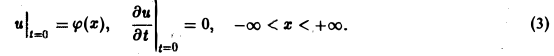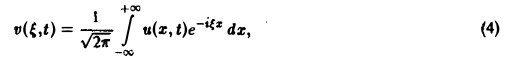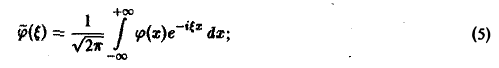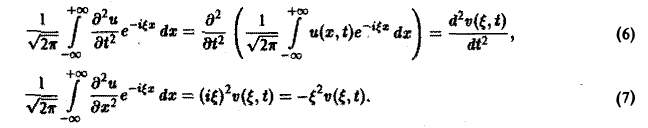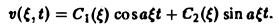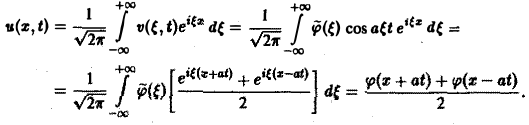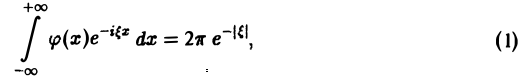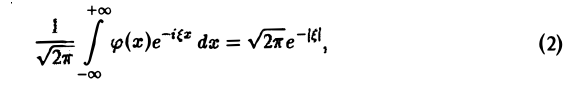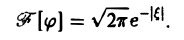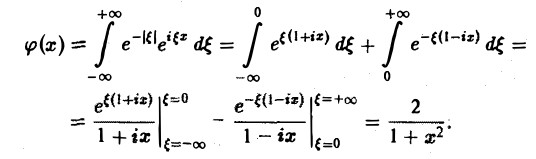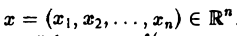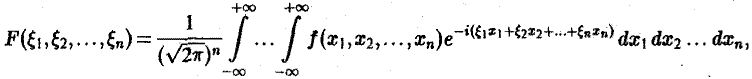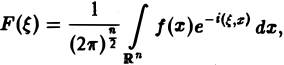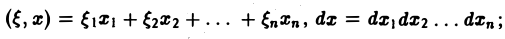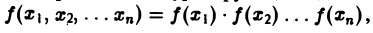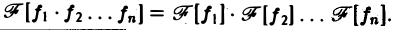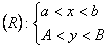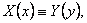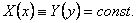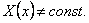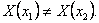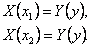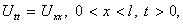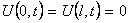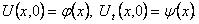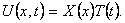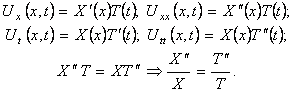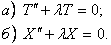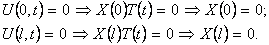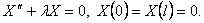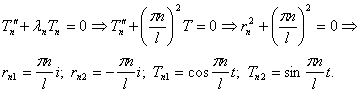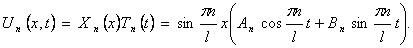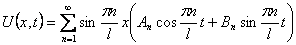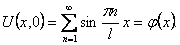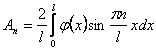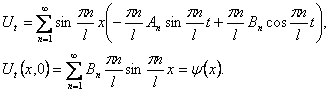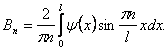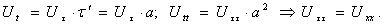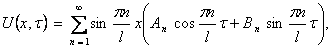Преобразование Фурье с примерами решения и образцами выполнения
Одним из мощных средств исследования задач математической физики является метод интегральных преобразований.
Пусть функция f(x) задана на интервале (а, 6), конечном или бесконечном. Интегральным преобразованием функции f(х) называется функция (*)
где К(х, w) — фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существует в собственном или несобственном смысле).
Интеграл Фурье
Всякая функция f(x), которая на отрезке [— l, l] удовлетворяет условиям разложимости в ряд Фурье, может быть на этом отрезке представлена тригонометрическим рядом (1)
Коэффициенты аn и bn ряда (1) определяются по формулам Эйлера—Фурье:
(2)
Ряд в правой части равенства (1) можно записать в иной форме. С этой целью внесем в него из формул (2) значения коэффициентов аn и bn, подведем под знаки интегралов cos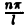 
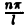
х и sin х (что возможно, поскольку переменной интегрирования является τ) и используем формулу для косинуса разности. Будем иметь
(3)
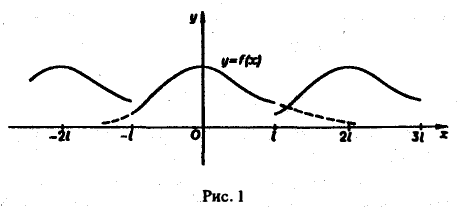
Если функция f(x) первоначально была определена на интервале числовой оси, большем, чем отрезок [-l, l] (например, на всей оси), то разложение (3) воспроизведет значения этой функции только на отрезке [-l, l] и продолжит ее на всю числовую ось как периодическую функцию с периодом 2l (рис. 1).
Поэтому, если функция f(x) (вообще говоря, непериодическая) определена на всей числовой оси, в формуле (3) можно попытаться перейти к пределу при l → +∞. При этом естественно потребовать выполнения следующих условий:
1, f(x) удовлетворяет условиям разложимости в ряд Фурье на любом конечном отрезке оси Ох;
2. функция f(x) абсолютно интегрируема на всей числовой оси,
При выполнении условия 2 первое слагаемое правой части равенства (3) при l → +∞ стремится к нулю. В самом деле,
Попытаемся установить, во что перейдет в пределе при l → +∞ сумма в правой части (3). Положим
так, что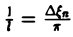 
. Тогда сумма в правой части (3) примет вид
В силу абсолютной сходимости интеграла эта сумма при больших l мало отличается от выражения
которое напоминает интегральную сумму для функции переменного ξ
составленную для интервала (0, + ∞) изменения Поэтому естественно ожидать, что при l → +∞ (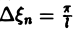 
→ 0) сумма (5) перейдет в интеграл
С другой стороны, при l → +∞ (х фиксировано) из формулы (3) вытекает, что
и мы получаем равенство
(7)
Достаточное условие справедливости формулы (7) выражается следующей теоремой.
Теорема:
Если функция f(x) абсолютно интегрируема на всей числовой оси — ∞ 
При этом во всякой точке xq, являющейся точкой разрыва 1-го рода функции f(x), значение интеграла в правой части (7) равно
Формулу (7) называют интегральной формулой Фурье, а стоящий в ее правой части интеграл — интегралам Фурье.
Если воспользоваться формулой для косинуса разности, то формулу (7) можно записать в виде (8)
Функции а( ξ ), b( ξ ) являются аналогами соответствующих коэффициентов Фурье an и bn 2π-периодической функции, но последние определены для дискретных значений п, в то время как а( ξ ), b( ξ ) определены для непрерывных значений ξ ∈ (— ∞, + ∞).
Комплексная форма интеграла Фурье
Предполагая f(x) абсолютно интегрируемой на всей оси Ох, рассмотрим интеграл
Этот интеграл равномерно сходится для — ∞ 
и потому представляет собой непрерывную и, очевидно, нечетную функцию от ξ. Но тогда
С другой стороны, интеграл
есть четная функция переменной так что
Поэтому интегральную формулу Фурье можно записать так:
на мнимую единицу i и прибавим к равенству (10). Получим
откуда, в силу формулы Эйлера (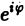
= cos φ + i sin φ), будем иметь
(11)
Это — комплексная форма интеграла Фурье. Здесь внешнее интегрирование по ξ понимается в смысле главного значения по Коши:
Преобразование Фурье. Косинус- и синус-преобразования Фурье
Пусть функция f(x) является кусочно-гладкой на любом конечном отрезке оси Ох и абсолютно интегрируема на всей оси.
Определение:
называется преобразованием Фурье функции f(x) (спектральной функцией).
Это — интегральное преобразование функции f(x) на интервале (- ∞ ,+ ∞) с ядром
Используя интегральную формулу Фурье
Это так называемое обратное преобразование Фурье, дающее переход от F( ξ ) к f(x). Иногда прямое преобразование Фурье задают так:
Тогда обратное преобразование Фурье определится формулой
Преобразование Фурье F( ξ ) функции f(х) определяют также следующим образом:
Тогда, в свою очередь,
При этом положение множителя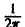 
достаточно произвольно: он может входить либо в формулу (1″), либо в формулу (2″).
Пример:
Найти преобразование Фурье функции
Это равенство допускает дифференцирование по ξ под знаком интеграла (получающийся после дифференцирования интеграл равномерно сходится, когда ξ принадлежит любому конечному отрезку):
Интегрируя по частям, будем иметь
Внеинтегральное слагаемое обращается в нуль, и мы получаем
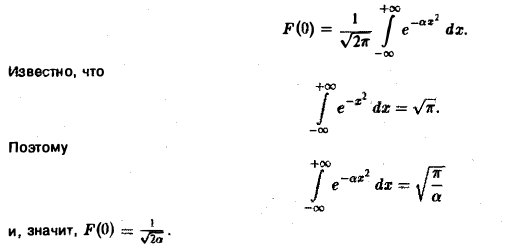
(С — постоянная интегрирования). Полагая в (4) ξ = 0, найдем С —F(0). В силу (3) имеем
В частности, для
Пример:
Разряд конденсатора через сопротивление. Рассмотрим функцию
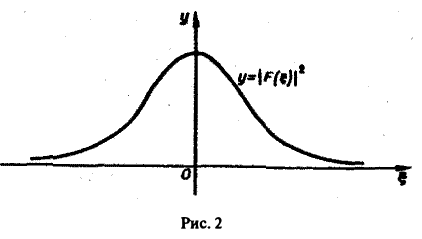
Для спектральной функции F( ξ ) получаем
Условие абсолютной интегрируемости функции f(x) на всей числовой оси является весьма жестким. Оно исключает, например, такие элементарные функции, как f(x) = 1. f(x) = x 3 , f(х) = cosx, f(х) = е х , для которых преобразования Фурье (в рассматриваемой здесь классической форме) не существует.
Фурье-образ имеют только те функции, которые достаточно быстро стремятся к нулю при |х| → + ∞ (как в примерах 1 и 2).
Косинус- и синус-преобразования Фурье
Используя формулу косинуса, разности, перепишем интегральную формулу Фурье
в следующем виде:
Пусть f(x) — четная функция. Тогда
так что из равенства (5) имеем
(6)
В случае нечетной f(x) аналогично получаем
(7)
Если f(х) задана лишь на (0, + ∞), то формула (6) продолжает f(x) на всю ось Ох четным образом, а формула (7) — нечетным.
Определение:
называется косинус-преобразованием Фурье функции f(x). Из (6) следует, что для четной функции f(x)
Это означает, что f(x), в свою очередь, является косинус-преобразованием для Fc( ξ ). Иными словами, функции f и Fc являются взаимными косинус-преобразованиями.
Определение:
называется синус-преобразованием Фурье функции f(x).
Из (7) получаем, что для нечетной функции f(х)
т.е. f и Fs являются взаимными синус-преобразованиями.
Пример:
Прямоугольный импульс. Пусть f(t) — четнaя функция, определенная следующим образом:
Воспользуемся полученным результатом для вычисления интеграла
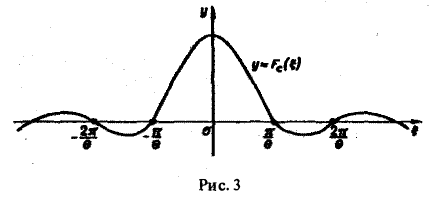
В силу формулы (9) имеем
В точке t = 0 функция f(t) непрерывна и равна единице.
Поэтому из (12′) получим
Амплитудный и фазовый спектры интеграла Фурье
Пусть периодическая с периодом 2π функция f(х) разлагается в ряд Фурье
Это равенство можно записать в виде
где Cn =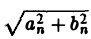 
— амплитуда колебания с частотой п, φn — фаза. На этом пути мы приходим к понятиям амплитудного и фазового спектров периодической функции.
Для непериодической функции f(x), заданной на (- ∞, + ∞), при определенных условиях оказывается возможным представить ее интегралом Фурье
осуществляющим разложение этой функции по всем частотам 0 
(прямое преобразование Фурье функции f(х)).
называется амплитудным спектром, а функция
(0 — фазовым спектром функции f(x).
Амплитудный спектр A (ξ) служит мерой вклада частоты ξ в функцию f(х).
Пример:
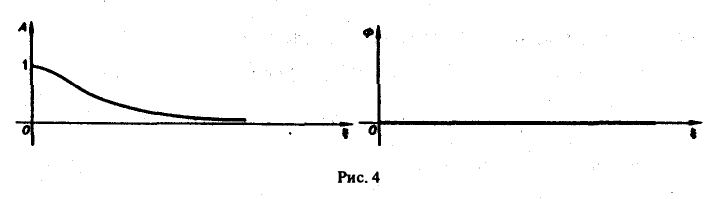
Найти амплитудный и фазовый спектры функции
Находим спектральную функцию
Графики этих функций изображены на рис. 4.
Свойства преобразования Фурье
1, Линейность. Если F( ξ ) и G( ξ ) — преобразования Фурье функций f(х) и g(х) соответственно, то при любых постоянных а и β преобразованием Фурье функции а f(х) + β g(х) будет функция a F( ξ ) + βG( ξ ).
Пользуясь свойством линейности интеграла, имеем
Таким образом, преобразование Фурье есть линейный оператор. Обозначая его через 
будем писать
Если F( ξ ) есть преобразование Фурье абсолютно интегрируемой на всей числовой оси функции f(х), то F( ξ ) ограничена при всех ξ ∈ (— ∞, + ∞).
Пусть функция f(х) абсолютно интегрируема на всей оси — ∞ 
— преобразование Фурье функции f(х). Тогда
Задача:
Пусть f(x) — функция, допускающая преобразование Фурье, h — действительное число. Функция fh(x) = f(x-h) называется сдвигом функции f(x). Пользуясь определением преобразования Фурье, показать, что
Задача:
Пусть функция f(x) имеет преобразование Фурье F( ξ ), h — действительное число. Показать, что
3. Преобразование Фурье и операция дифференцирования. Пусть абсолютно интегрируемая функция f(х) имеет производную f'(х), также абсолютно интегрируемую на всей оси Ох, так что f(х) стремится к нулю при |х| —► + ∞. Считая f'(х) гладкой функцией, запишем
Интегрируя по частям, будем иметь
Внеинтегральное слагаемое обращается в нуль (так как f(х) → 0 при |х| → + ∞), и мы получаем (1)
Таким образом, дифференцированию функции f(х) отвечает умножение ее образа Фурье [f] на множитель iξ.
Если функция f(х) имеет гладкие абсолютно интегрируемые производные до порядка m включительно и все они, как и сама функция f(х), стремятся к нулю при |x| → + ∞, то, интегрируя по частям нужное число раз, получим
Преобразование Фурье очень полезно именно потому, что оно заменяет операцию дифференцирования операцией умножения на величину iξ и тем самым упрощает задачу интегрирования некоторых видов дифференциальных уравнений.
Так как преобразование Фурье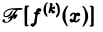 
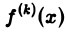
абсолютно интегрируемой функции 
есть ограниченная функция от ξ (свойство 2), то из соотношения (2) получаем для [f] следующую оценку:
Из этой оценки следует: чем больше функция f(х) имеет абсолютно интегрируемых производных, тем быстрее ее преобразование Фурье стремится к нулю при | ξ | → + ∞.
Замечание:
Условие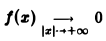 
является достаточно естественным, поскольку обычная теория интегралов Фурье имеет дело с процессами, которые в том или ином смысле имеют начало и конец, но не продолжаются неограниченно с примерно одинаковой интенсивностью.
4. Связь между скоростью убывания функции f(x) при |х| → + ∞ и гладкостью ее преобразования Фурье. Предположим, что не только f(x), но и ее произведение хf(х) является абсолютно интегрируемой функцией на всей оси Ох. Тогда преобразование Фурье
функции f(x) будет дифференцируемой функцией.
Действительно, формальное дифференцирование по параметру ξ подынтегральной функции приводит к интегралу
который является абсолютно и равномерно сходящимся относительно параметра Следовательно, дифференцирование возможно, и
т. е. операция умножения f(х) на аргумент х переходит после преобразования Фурье в операцию 
Если вместе с функцией f(х) абсолютно интегрируемыми на всей оси Ох являются функции хf(х)…..х m f(х), то процесс дифференцирования можно продолжить.
Получим, что функция F( ξ ) = [f(х)] имеет производные до порядка m включительно, причем
Таким образом, чем быстрее функция f(х) убывает при |х| → + ∞, тем более гладкой получается функция F( ξ ) = [f(х)].
Теорема:
О свертке. Пусть F1( ξ ) и F2( ξ ) — преобразования Фурье функций f1(x) и f2(x) соответственно. Тогда
причем двойной интеграл в правой части сходится абсолютно.
Положим х + у = т, так что у = т — х. Тогда будем иметь
или, меняя порядок интегрирования,
называется сверткой функций f(x) и f2(x) и обозначается символом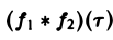 
. Формула (1) может быть теперь записана так:
Отсюда видно, что преобразование Фурье свертки функций f1(x) и f2(x) равно умноженному на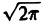 
произведению преобразований Фурье свертываемых функций,
Замечание:
Нетрудно установить следующие свойства свертки:
Приложения преобразования Фурье
1, Пусть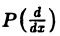 
— линейный дифференциальный оператор порядка m с постоянными коэффициентами,
(аo, a1,… ,ат = const). Используя формулу для преобразования Фурье производных функции у(х), находим
Рассмотрим дифференциальное уравнение
где 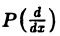— введенный выше дифференциальный оператор.
Предположим, что искомое решение у(х) имеет преобразование Фурье y(ξ), а функция f(x) имеет преобразование f( ξ ). Применяя преобразование Фурье к уравнению (1), получим вместо дифференциального алгебраическое уравнение на оси Oξ относительно y(ξ)
так что формально
где символ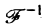 
обозначает обратное преобразование Фурье.
Основное ограничение применимости этого метода связано со следующим фактом. Решение обыкновенного дифференциального уравнения с постоянными коэффициентами содержит функции вида
Они не являются абсолютно интегрируемыми на оси — ∞ 
(а = const), при начальных условиях
Это — задача о свободных колебаниях бесконечной однородной струны, когда задано начальное отклонение φ(х) точек струны, а начальные скорости отсутствуют.
Поскольку пространственная переменная х изменяется в пределах от — ∞ до + ∞, подвергнем уравнение и начальные условия преобразованию Фурье по переменной х. Будем предполагать, что
1) функции u(z, t) и φ(x) — достаточно гладкие и стремятся к нулю при \х\ → + ∞ и ∀t ≥ О настолько быстро, что существуют преобразования Фурье
2) допустимы операции дифференцирования, так что
Умножая обе части (2) на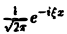 
и интегрируя по x от — ∞ до + ∞, получим
а из начальных условий (3) найдем
Таким образом, применяя к задаче (2)-(3) преобразование Фурье, приходим к задаче Коши (8)—(10) для обыкновенного дифференциального уравнения, где ξ — параметр. Решением уравнения (8) является функция
Из условий (9) и (10) находим, что С1( ξ ) = φ( ξ ). C2( ξ ) = 0, так что v( ξ, t) = φ( ξ )cos aξt. Применяя обратное преобразование Фурье, получим
Это частный случай формулы Даламбера решения задачи (2)-(3).
2. Преобразование Фурье может быть использовано при решении некоторых интегральных уравнений, т. е. уравнений, в которых неизвестная функция входит под знак интеграла.
Рассмотрим, например, уравнение
где φ(х) — искомая функция. Записав (1) в виде
замечаем, что левую часть (2) можно рассматривать как преобразование Фурье функции φ(х), так что (2) равносильно следующему равенству:
Тогда по формуле обращения
Функция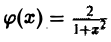 
есть решение уравнения (1).
Понятие о многомерном преобразовании Фурье
Преобразование Фурье:
Многомерным преобразованием Фурье абсолютно интегрируемой функции f(х1, х2,…, хb) называется функция
символ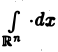 
обозначает интегрирование по всему пространству R n .
Свойства многомерного преобразования аналогичны соответствующим свойствам преобразования Фурье функции одной переменной. В специальном случае, когда
Дополнение к преобразованию Фурье
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Лекция 3. Метод Фурье
Метод Фурье — один из распространенных и эффективных методов решения уравнений с частными производными. Этот метод часто встречается и под другими названиями: метод разделения переменных или метод собственных функций.
Общая схема метода Фурье.
Основная идея этого метода состоит в том, что решение задачи для уравнения с частными производными сводится к решению вспомогательных задач для уравнений с меньшим числом независимых переменных. В частности, если заданное уравнение содержит две независимые переменные, то вспомогательные задачи будут уже зависеть только от одной переменной. Таким образом решение уравнения с частными производными сводится к решению обыкновенных дифференциальных уравнений.
При применении метода Фурье удобно использовать следующую лемму.
Основная лемма метода Фурье.
Если в прямоугольнике R плоскости XOY:
для некоторых функций выполняется тождество
то в этом случае
Доказательство. Предположим противное, т.е. что
Тогда существуют значения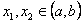 
такие, что
Рассмотрим точки (x1,y) и (x2,y), принадлежащие прямоугольнику R. На R справедливо тождество (8), а поэтому
Сравнивая эти равенства, приходим к противоречию с нашим предположением. Следовательно X(x) = const, а тогда Y(y)=const.
Решение первой начально-краевой задачи для волнового уравнения.
Рассмотрим волновое уравнение
Граничные условия первого рода
И начальные условия
Решим эту задачу методом Фурье.
Шаг 1. Представим функцию U(x,t) в виде
Найдем частные производные Uxx и Utt и подставим в уравнение (9):
В полученном уравнении левая часть зависит только от x, а правая- только от t. Используя основную лемму, заключаем:
Из граничных условий (10) получим
Шаг 2. Решим задачу Штурма-Лиувилля
Она имеет собственные значения и собственные функции
Шаг 3. Подставим найденные значения λn в уравнение а) и решим его:
Шаг 4. Выпишем частные решения уравнения (9):
Для волнового уравнения эти решения называются собственными колебаниями. В лекции 6 мы изучим их подробнее. В силу линейности и однородности уравнения (9) линейная комбинация этих решений
Замечание 1. Здесь мы предполагаем, что полученный функциональный ряд равномерно сходится и его можно дважды почленно дифференцировать по x и по t в области 0 0. Об условиях, при которых это можно сделать, будет рассказано в лекции 5.
Шаг 5. Определим коэффициенты Anи Bn в формуле (12), используя начальные условия (11). Из первого начального условия получим
Равенство (13) означает, что начальная функция φ(x) разлагается в ряд Фурье по синусам, которые в данном случае являются собственными функциями Xn(x) задачи Штурма-Лиувилля.
Коэффициенты Фурье вычисляются по формулам
Из второго начального условия находятся коэффициенты Bn.
Вычислив коэффициенты An и Bn для конкретных начальных функций и подставив их значения в (12), мы получим решение первой начально-краевой задачи.
Замечание 2. Используя формулу (12), можно получить решение первой начально-краевой задачи для уравнения колебания струны: Для этого проведем замену переменной τ=at и получим
При этом начальное условие не изменится, а условие преобразуется к виду Тогда решение задачи в переменных (x,τ) будет иметь вид
Возвращаясь к переменным (x,t), получим
http://vicaref.narod.ru/PDE/index3.htm