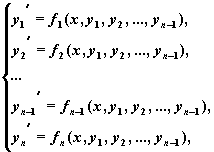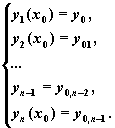Решение дифференциальных уравнений в маткаде odesolve
Для решения дифференциальных уравнений Mathcad предоставляет пользователю библиотеку встроенных функций Differential Equation Solving, предназначенных для численного решения дифференциальных уравнений.
| подробная информация о функции odesolve, примеры |
| подробная информация о функциях, примеры |
ODESOLVE
Встроенная функция odesolve предназначена для решения дифференциальных уравнений, линейных относительно старшей производной. В отличие от других функций библиотеки Differential Equation Solving, odesolve решает дифференциальные уравнения, записанные в общепринятом в математической литературе виде.
- Функция odesolve решает для уравнений вида
a(x) y(n) + F(x, y, y’ , . y (n-1) )=f(x)
задачу Коши
y(x0 )=y0 , y'(x0 )=y0,1 , y»(x0 )=y0,2 , . y (n-1) (x0 )=y0,n-1
или простейшую граничную задачу
y (k) (a)=ya,k , y (m) (b)=yb,k , 0 + ), а для записи производных можно использовать как оператор дифференцирования, так и знак производной, например, вторую производную можно вводить в видеили в виде y»(x). При этом необходимо обязательно записывать аргумент искомой функции.
- Для того чтобы вывести в рабочий документ значения решения в любой точке промежутка интегрирования, достаточно ввести имя функции Y, указать в скобках значение аргумента и знак равенства.
- Значения решения в любой точке промежутка интегрирования можно использовать в дальнейших вычислениях, достаточно ввести в нужном месте имя функции Y, указав в скобках значение аргумента.
Полную информацию о правилах использования функции odesolve можно получить во встроенном справочнике Mathcad в разделе Overview fnd Tutorials.
Функции для решения систем, записанных в нормальной форме
Встроенные функции Mathcad, предназначенные для решения задачи Коши и граничных задач, решают их для нормальных с и с т е м обыкновенных дифференциальных уравнений. Задачи для уравнений высших порядков сводятся к соответствующим задачам для нормальных с и с т е м.
Рассмотрим задачу Коши:
Численное решение этой задачи состоит в построении таблицы приближенных значений
yi,1 , yi,2 , . yi,N
решения y1 (x), y2 (x), . yN (x)
на отрезке [x0 , xN ] в точках
x1 , x2 , . xN, которые называются узлами сетки.
Обозначив
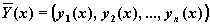
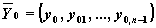
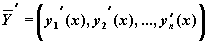
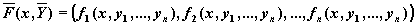
где 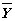
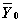
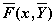
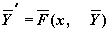
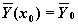
В Mathcad решить задачу Коши для такой системы можно с помощью следующих функций:
- rkfixed(y, x1, x2, npoints, D) —решение задачи на отрезке методом Рунге—Кутты с постоянным шагом;
- Rkadapt(y, x1, x2, npoints, D) —решение задачи на отрезке методом Рунге—Кутты с автоматическим выбором шага;
- rkadapt(y, x1, x2, acc, npoints, D, kmax, save) —решения задачи в заданной точке методом Рунге-Кутты с автоматическим выбором шага;
- Bulstoer(y, x1, x2, npoints, D) —решение задачи на отрезке методом Булирша-Штера;
- bulstoer(y, x1, x2, acc, npoints, D, kmax, save) —решение задачи в заданной точке методом Булирша—Штера;
- Stiffr(y, x1, x2, acc, D, J) — решение задачи для жестких систем на отрезке с использованием алгоритма Розенброка;
- stiffr(y, x1, x2, acc, D, J, kmax, save) —решения задач для жестких систем на отрезке с использованием алгоритма Розенброка;
- Stiffb(y, x1, x2, acc, D, J) —решение задачи для жестких систем на отрезке с использованием алгоритма Булирша—Штера;
- stiffb(y, x1, x2, acc, D, J, kmax, save) —решение задач для жестких систем в заданной точке с использованием алгоритма Булирша—Штера.
Смысл параметров для всех функций одинаков и определяется математической постановкой задачи:
y — вектор начальных условий 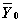
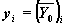
x1, x2 — начальная и конечная точки отрезка интегрирования системы; для функций, вычисляющих решение в заданной точке, x1 — начальная точка, x2 — заданная точка;
npoints — число узлов на отрезке [x1, x]; при решении задачи на отрезке результат содержит npoints+1 строку;
D — имя вектор-функции D(x,y) правых частей 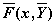
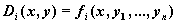
J — имя матрицы-функции J(x,y) размерности n x (n+1), в первом столбце которой хранятся выражения частных производных по x правых частей системы, а в остальных n столбцах содержится матрица Якоби правых частей: 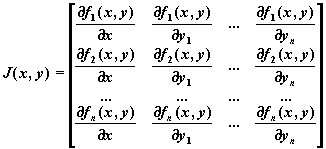
acc — параметр, контролирующий погрешность решения при автоматическом выборе шага интегрирования (если погрешность решения больше acc, то шаг сетки уменьшается; шаг уменьшается до тех пор, пока его значение не станет меньше save );
kmax — максимальное число узлов сетки, в которых может быть вычислено решение задачи на отрезке, максимальное число строк в результате;
save — наименьшее допустимое значение шага неравномерной сетки.
Результат работы функции — матрица, содержащая n+1; ее первый столбец содержит координаты узлов сетки, второй столбец — вычисленные приближенные значения решения y1 (x) в узлах сетки, (k+1) -й — значения решенияyk (x) в узлах сетки.
При решении задачи Коши для дифференциального уравнения первого порядка результат вычислений всех приведенных выше функций — матрица, в первом столбце которой содержатся координаты узлов сетки x0 , x1 , . xN, а во втором — значения приближенного решения в соответствующих узлах.
При исследовании автономных систем дифференциальных уравнений второго порядка полезную информацию можно получить рассматривая интегральные и фазовые кривые системы.
При исследовании автономных систем дифференциальных уравнений второго порядка полезную информацию о свойствах решений можно получить, построив векторное поле системы.
Запишем автономную систему второго порядка
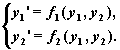
Эта система полностью определяется заданием векторного поля 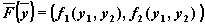
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Решение дифференциальных уравнений в маткаде odesolve
Глава 5. Решение дифференциальных уравнений
5 .1 Вычислительный блок Given– Odesolve
Применение функции Odesolve требует записи вычислительного блока, состоящего из трех частей:
1) ключевого слова Given (Дано);
2) дифференциального уравнения и начальных или граничных условий к нему;
3) функции о desolve ( x , xk , n ) (решение ОДУ), где x – имя переменной, относительно которой решается уравнение; xk – конец интервала интегрирования (начало интервала интегрирования указано ранее, в начальных условиях); n – необязательный внутренний параметр, определяющий число шагов интегрирования, на которых решается дифференциальное уравнение.
Примеры использования функции Odesolve приведены на рис. 5.2–5.5.
Given



граничные условия можно задавать лишь в двух точках:
в начале и в конце интервала интегрирования
Рис. 5.2 Решение уравнения с граничными условиями
Если вид дифференциального уравнения изменяется с изменением аргумента, например, уравнение содержит ступенчатую разрывную функцию, то такое уравнение можно записать с использованием условия, то есть записать несколько уравнений в виде одного уравнения (рис. 5 . 3 ).
MathCAD позволяет записать условие несколькими способами:
– с использованием булевых операторов:

– с использованием функции if :

В данном случае невозможно записать условие с использование условного оператора программирования if , так как вертикальной черте (обязательному признаку программирования) должен предшествовать оператор присваивания :=, тогда как в нашем случае использован знак + или знак логического равенства =.
поменяйте местами закрашенные выражения
Given



Рис. 5.3 Объединение двух дифференциальных уравнений в одно
В MathCAD все встроенные функции для решения дифференциальных уравнений требуют записи производной высшего порядка в явном виде. Однако, как показано на рис. 5 . 2 , присутствие коэффициента (постоянного или переменного) перед производной высшего порядка – не помеха при решении ОДУ. Если уравнение есть сложная функция от высшей производной, предварительно надо решить это уравнение алгебраически относительно высшей производной. На рис. 5 .4. исходное уравнение решено символьно относительно у'(х). Для выполнения этой операции надо выделить переменную, затем в главном меню выбрать команду Symbolics → Variable → Solve (Символьные вычисления→Переменная→Решить). Найденный результат подставлен в дифференциальное уравнение, которое решено с помощью функции Odesolve.
В MathCAD 2001 i возможности функции Odesolve были расширены. Теперь она может решать и системы дифференциальных уравнений. При этом несколько изменяется обращение к ней.
Дано уравнение
решим его относительно у'(х)

уравнение в стандартном виде подставим в блок Given — Odesolve
два корня уравнения дают решение ОДУ
Given 

Рис. 5.4 Приведение дифференциального уравнения к стандртному виду и его решение
Обращение к функции для решения одного уравнения выглядит так:
о desolve ( x , xk , n ),
для решения системы дифференциальных уравнений–
о desolve ((вектор имен неизвестных), x , xk , n ).
Н а рис. 5 .5 приведено решение системы из трех дифференциальных уравнений первого порядка. соответственно, вектор имен неизвестных содержит имена трех неизвестных, х, у и z . Граничные условия заданы в точке t = –1. конечная точка интервала интегрирования t =3. Следовательно, интервал интегрирования от –1 до 3. Конечное значение всегда должно быть больше начального.
Если график строится для значений, выходящих за пределы интервала интегрирования, MathCAD экстраполирует значения функции за пределы интервала интегрирования, получая чаще всего неправдоподобные результаты.



Рис. 5.5 Решение системы ОДУ функцией Odesolve
В MathCAD 2001 i у функции Odesolve появилась возможность принимать в качестве ограничений алгебраические уравнения (рис. 5.6 и 5.7), но только в задачах с начальными условиями.
Рассмотрим механизм работы блока Odesolve: блок Odesolve преобразует заданные дифференциальные уравнения к стандартному виду, используемому функциями rkfixed и Rkadapt . С помощью указанных функций он решает систему ОДУ (или одно ОДУ) с начальными условиями. В результате расчета получают массив значений функции и ее производные.
Далее используются функции интерполяции lspline и interp , преобразующие массив решений системы ОДУ в функцию, которую затем можно дифференцировать или интегрировать. Необязательный параметр steps в обращении к функции Odesolve как раз и задает число точек интерполяции. Чем больше steps , тем выше точность интерполяции, но тем больше время решения задачи.
При решении системы ОДУ есть возможность выбрать метод решения. Для этого надо установить курсор на слове Odesolve и нажать правую кнопку мыши. В открывшемся контекстном меню выбрать Fixed (Решение с фиксированным шагом функцией rkfixed ), Adaptive (Решение с переменным шагом функцией Rkadapt ) или Stiff (Решение жесткой системы ОДУ функцией Radau ) , как показано на рис. 5.7 .



требуется 6 начальных условий:





Рис. 5. 6 Решение системы ОДУ с алгебраическими ограничениями функцией Odesolve
Given 


Рис. 5.7 В ыбор метода решения дифференциальных уравнений
Решение дифференциальных уравнений в маткаде odesolve
Электронный курс по MathCAD



5.2 Решение дифференциальных уравнений и систем.(Задача Коши и граничные задачи).
Решение одиночного дифференциального уравнения.
Для численного решения одиночного дифференциального уравнения в MathCAD имеется функция Odesolve, с помощью которой может быть решена как задача Коши для обыкновенного дифференциального уравнения, так и граничная задача. Эта функция входит в состав блока решения и сявляется его заключительным ключевым словом.
Odesolve(x,b,[step]) — Возвращает функцию, которая является решением дифференциального уравнения. Используется в блоке с оператором Given.
x — переменная интегрирования, действительное число
b — конечная точка отрезка интегрирования
step — величина шага по переменной интегрирования (необязательный аргумент)
Замечания:
- Уравнение должно быть линейным относительно старшей производной.
- Число заданных начальных или граничных условий внутри блока должно быть равно порядку уравнения.
- При записи уравнения для обозначения производных функции используйте специальные кнопки с панели Math или ‘ (штрих) — [Ctrl+F7], для знака равенства = [Ctrl+=] (в том числе и для дополнительных условий).
- Конечная точка должна быть больше начальной.
- Не допускаются начальные и граничные условия смешанного типа (f ‘(a)+f(a)=5).
- Искомая функция в блоке дложна быть обязательно с аргументом ( f(x))
 |  |
Численное решение задачи Коши для дифференциальных уравнений и систем.
Для численного решения задачи Коши для дифференциальных уравнений и систем могут быть использованы функции:
rkfixed(y,x1,x2,n,F) — возвращает матрицу решений системы уравнений методом Рунге-Кутта 4-го порядка при фиксированном шаге по x
rkadapt(y,x1,x2,n,F) — ищет решение с переменным шагом ( там, где решение меняется медленнее, шаг увеличивается, а в области быстрого изменения решения шаг функции уменьшается). Возвращается решение с равным шагом. Функция работает быстрее, чем rkfixed
Bulstoer(y,x1,x2,n,F) — дает более точное решение (методом Bulirsch-Stoer)
Агрумкнты вышеуказанных функций:
y — вектор начальных условий
x1,x2 — границы интервала для поиска решения
n — количество точек на интервале
F(x,y) — вектор-функция первых производных
При решении дифференциальных уравнений порядка выше первого (или систем уравнений, выше первого порядка) исходное уравнение (систему) необходимо преобразовать к системе дифференциальных уравнений первого порядка.
В результате работы укзанных функций рассчитывается матрица, количество стобцов которой равно порядку уравнения +1(или сумме порядков уравнений в системе +1), а количество строк равно параметру n. Первый столбец содержит значения независимой переменной, второй — значение функции, третий — для диф. уравнений 2-го порядка — значение производной искомой функции (если решается система двух уравнений 1-го порядка, то третий столбец будет содержать значения второй функции). Для выделения решений (функций или их производных) можно воспользоваться стандартным оператором вывода столбцов матрицы M < >
Если матрица правых частей дифференциальных уравнений почти вырождена, то такие системы называются жесткими. В этом случае решения, возвращаемые функцией rkfixed будет неустойчивым и для решения таких систем необходимо применять функции Stiffb , Stiffr
Stiffb(y,x1,x2,n,F,J) — ищет решение диф. уравнения или системы дифференциальных уравнений методом Bulirsch-Stoer
Stiffr(y,x1,x2,n,F,J) — ищет решение диф. уравнения или системы дифференциальных уравнений методом Rosenbrock
 |
 |
 |
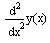 или в виде y»(x). При этом необходимо обязательно записывать аргумент искомой функции.
или в виде y»(x). При этом необходимо обязательно записывать аргумент искомой функции.