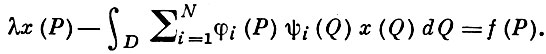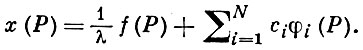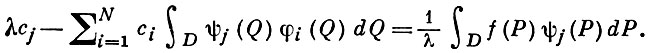Решение интегральных уравнений с вырожденным ядром

Решения интегральных уравнений онлайн

В этом разделе мы рассмотрим типовые задачи по интегральным уравнениям с решениями. Интегральное уравнение содержит неизвестную функцию под знаком интеграла (по аналогии как дифференциальное — функцию под знаком дифференциала:)).

Выделяют два основных класса интегральных уравнений: уравнения Фредгольма I и II рода:

$$ (I) \quad \int_a^b K(x,s)u(s)ds = f(x),\\ (II) \quad u(x)=\int_a^b K(x,s)u(s)ds + f(x). $$

В случае переменного верхнего предела интегрирования получаем соответственно уравнение Вольтерра I и II рода:

$$ (I) \quad \int_a^x K(x,s)u(s)ds = f(x),\\ (II) \quad u(x)=\int_a^x K(x,s)u(s)ds + f(x). $$

Это линейные неоднородные уравнения (при $f(x)=0$ — однородные), иногда рассматриваются более общий случай с параметром $\lambda$ перед интегралом.

Ниже вы найдете примеры нахождения решений интегральных уравнений, собственных значений и функций, исследования ядра, применения интегральных уравнений для решения других задач.

Примеры решений интегральных уравнений

Задача 1. Пользуясь теоремой Гильберта-Шмидта, исследовать и решить интегральное уравнение 2-го рода $(E+\lambda A)x=y$ в гильбертовом пространстве $X$.

Задача 2. Найти собственные значения и собственные функции уравнения:

$$ y(x)=\lambda \int_0^1 (\cos 2\pi x +2x \sin 2\pi t +t \sin \pi x)y(t)dt. $$

Задача 3. Решить уравнение Вольтерры, сведя его к обыкновенному дифференциальному уравнению.

Задача 4. Решить или установить неразрешимость уравнений с вырожденным ядром.

Задача 5. Решить интегральное уравнение, сведя его предварительно к обыкновенному дифференциальному уравнению.

Задача 6. Найти резольвенту для интегрального уравнения Вольтерры со следующим ядром $K(x,t)=x^<1/3>t^<2/3>$.

Задача 7. Исследовать решения уравнения с вырожденным ядром при различных значениях параметра $\lambda$ (ограничиться случаем вещественных характеристических чисел).

$$ y(x)-\lambda \int_0^1 x y(t)dt = \sin 2\pi x. $$

Задача 8. Для симметричного ядра $$K(x,t) = \frac<1> <2>\sin |x-t| \quad (0 \le, x,t \le \pi)$$ найти характеристические числа и соответствующие им собственные функции, сводя интегральное уравнение к однородной краевой задаче для обыкновенного дифференциального уравнения.

Задача 9. Решить краевую задачу, используя функцию Грина

Задача 10. Применяя преобразование Лапласа, решить интегральное уравнение

Помощь с интегральными уравнениями

Если вам нужна помощь с решением задач и контрольных по интегральным уравнениям (и другим разделам математического и функционального анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 200 рублей , оформление производится в Word, срок от 1 дня.

ВЫРОЖДЕННОЕ ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ

ВЫРОЖДЕННОЕ ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ — линейное интегральное уравнение Фредгольма с вырожденным ядром. Общий вид В. и. у.:

Интегрирование производят по области D (вообще n-мерного) евклидова пространства, Р и Q — точки из D, λ — действительный или комплексный параметр, а функции, входящие в (1), суммируемы с квадратом на D. Решение В. и. у. (1) ищется в виде

Коэффициенты c_i находятся из системы линейных алгебраич. уравнений

Если система (2) при заданном X имеет единственное решение, то уравнение (1) также однозначно разрешимо. Те значения λ ≠ 0 (их не более N), при к-рых определитель системы (2) равен 0, являются собственными значениями. Условия разрешимости В. и. у. (1) даются Фредгольма альтернативой. При λ = 0 В. и. у. (1) есть уравнение Фредгольма I рода; для его разрешимости необходимо и достаточно, чтобы функция f могла быть представлена в виде линейной комбинации функций φ_i. Тогда В. и. у. (1) имеет решение, представимое в виде

при этом коэффициенты d_j определяются однозначно, а ψ есть функция, удовлетворяющая условиям

Важность В. и. у. для общей теории уравнений Фредгольма обусловлена тем, что решение любого уравнения Фредгольма II рода может быть с любой точностью в среднем квадратическом (и в нек-рых других метриках) приближено решениями В. и. у. Их вырожденные ядра в том или ином смысле аппроксимируют ядро исходного уравнения.

Абстрактным аналогом и обобщением В. и. у. служит линейное операторное уравнение вида

где х и f принадлежат банахову пространству Е, а оператор А имеет конечномерную область значений. Свойства таких уравнений аналогичны свойствам В. и. у. (1).

Лит.: [1] Михлин С. Г., Лекции по линейным интегральным уравнениям, М., 1959.

А. Б. Бакушинский.

1. Математическая Энциклопедия. Т. 1 (А — Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] — М., «Советская Энциклопедия», 1977, 1152 стб. с илл.