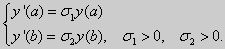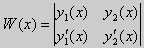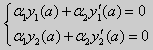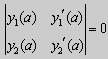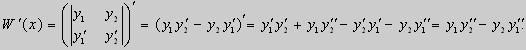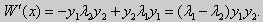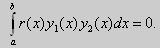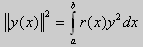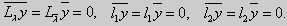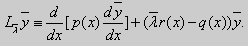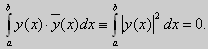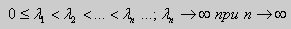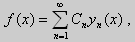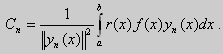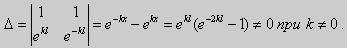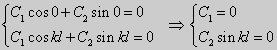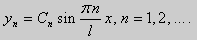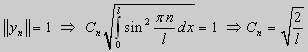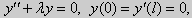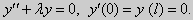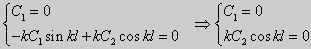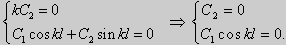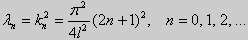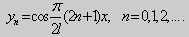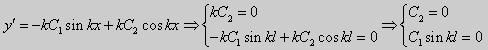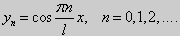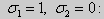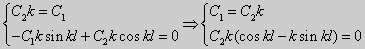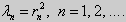Лекция 4. Краевые задачи для дифференциальных уравнений. Задача Штурма-Лиувилля.
Будем рассматривать однородное линейное уравнение второго порядка
Ly ≡ a2(x)y» + a1(x)y’ + a0(x)y = 0. Его можно записать по-другому:
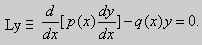 | (15) |
Однородное уравнение Ly = 0 и неоднородное Ly = f, как известно, имеют бесконечное множество решений. На практике часто бывает нужно из множества решений выделить только одно. Для этого задают некоторые дополнительные условия. Если это начальные условия у(х0) = уo, y'(xo) = y1, то получают задачу Коши. Если задают дополнительные условия на концах некоторого отрезка, то получают задачу, которая называется краевой задачей. Условия, которые задаются на концах отрезка, называются краевыми условиями. Краевые условия иногда именуют также граничными условиями и тогда говорят о граничной задаче.
Мы будем задавать линейные краевые условия вида
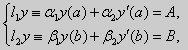 | (16) |
где α1, α2, β1, β2, A, B — заданные числа, причем по крайней мере одно из чисел α1, α2, и одно из чисел β1, β2, отличны от нуля. Если в (16) хотя бы одно из чисел А и В не равно нулю, то краевые условия называют неоднородными. Если А = В = 0, то условия (16) называются однородными. Краевая задача называется однородной, если рассматривается однородное уравнение (15) Ly = 0 и однородные краевые условия (16). Решением краевой задачи называется такое решение дифференциального уравнения, которое удовлетворяет заданным краевым условиям. Заметим сразу, что однородная краевая задача всегда имеет решение у ≡ 0 (тривиальное решение).
Наряду с уравнением (15) рассмотрим уравнение
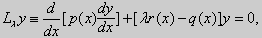 | (17) |
содержащее некоторый числовой параметр λ. Здесь функции р(х), q(x), r(x) действительные, а число λ может быть, вообще говоря, и комплексным. Краевая задача (17), (16) при А = В = 0 является однородной. Поэтому при любых λ она имеет тривиальное решение. Нас будут интересовать такие значения λ, при которых эта задача обладает не только тривиальными решениями.
Задача Штурма-Лиувилля. Найти те значения параметра λ, при которых уравнение (17) имеет нетривиальное решение, удовлетворяюшее однородным краевым условиям (16). В дальнейшем будем ее записывать в виде
Из множества краевых условий вида (16) ограничимся тремя частными случаями: 1) краевые условия первого рода 2) краевые условия второго рода 3) краевые условия третьего рода Общая задача Штурма-Лиувилля будет обладать свойствами, очень похожими на свойства в этих простых случаях, если на коэффициенты уравнения (17) наложить дополнительные условия: р(х), q(x), f(x) -непрерывные функции, причем р(х) имеет, кроме того, непрерывную производную на [а, b], р(х) > 0, q(x) ≥ 0. Основные свойства собственных значений и собственных функций задачи Штурма-Лиувилля. Лемма. Определитель Вронского двух собственных функций задачи Штурма-Лиувилля на концах отрезка [а, b] равен нулю. Доказательство. Напомним, что определителем Вронского функций у = y1(x) и у = у2(x) называется определитель вида Рассмотрим однородные краевые условия общего вида (16). Пусть у1(x) и у2(x) — две любые собственные функции. Это означает, что в точке x = а выполняются равенства Числа α1, и α2 не могут одновременно равняться нулю. Значит, алгебраическая система двух однородных уравнений с двумя неизвестными имеет ненулевое решение. Это возможно только в том случае, когда определитель этой системы равен нулю: Этот определитель совпадает с определителем Вронского в точке x = а, то есть W(a) = 0. Аналогичные рассуждения, проведенные для точки x = b, показывают, что W(b) = 0. Свойство 1. Две собственные функции задачи Штурма-Лиувилля, соответствующие одному и тому же собственному значению λ, линейно зависимые. Доказательство. Так как собственные функции являются решениями одного и того же однородного уравнения (17) (по условию число λ одно), то в случае их линейной независимости определитель Вронского не равен нулю ни в одной точке отрезка [а, b]. Это противоречит только что доказанной лемме. Следовательно, y1(x) и у2(x) — линейно зависимые функции. Свойство 2. Две собственные функции у1(x) и у2(x), соответствующие различным собственным значениям λ1 и λ2 (λ1 ≠ λ2), на отрезке [а, b] ортогональны. Доказательство этого свойства проведем для собственных функций такой задачи, в которой уравнение имеет вид (18). Составим определитель Вронского функций у1 и у2 и продифференцируем его: Так как у1 и у2 — решения уравнения (18) при λ = λ1 и λ = λ2, соответственно, то получим Проинтегрируем по отрезку [а, b] левую и правую части полученного равенства. С учетом леммы будем иметь Если уравнение, входящее в задачу Штурма-Лиувилля, имеет вид (17), где r(х) > 0 и r(x) 1, то под ортогональностью функций в этом случае подразумевают ортогональность с весом r(х): две функции y1(x) и у2(х) ортогональны на отрезке [а, b] с весом r(x), если Под нормой функции ||у(x)|| в этом случае также подразумевают весовую норму: Свойство 3. Собственные функции, соответствующие различным собственным значениям, образуют линейно независимую систему функций. Это утверждение вытекает из попарной ортогональности собственных функций, соответствующих различным собственным значениям (см. свойство 2). Свойство 4. Собственные значения задачи Штурма-Лиувилля действительные. Доказательство. Предположим, что задача Штурма-Лиувилля Здесь черта означает переход к комплексно сопряженному выражению. В нашем случае Значит число Отсюда следует, что у(x) ≡ 0 на [а, b]. Значит ни одно комплексное число λ не может быть собственным значением. Свойство 5. Пусть коэффициенты уравнения (17) удовлетворяют условиям: р(х), q(x), r(x) — непрерывные функции и, кроме того, р(х) имеет непрерывную производную на [а, b], р(х) > 0, q(x) > 0, r(х) > 0. Тогда задача Штурма-Лиувилля Теорема Стеклова.Всякая непрерывная функция f(x), удовлетворяющая однородным краевым условиям : l1f = 0 и l2f = 0 , и имеющая непрерывные производные до второго порядка на отрезке [а, b], разлагается на этом отрезке в сходящийся ряд Фурье по собственным функциям yn(х) задачи Штурма-Лиувилля где коэффициенты Фурье Сn вычисляются по формулам: Эта теорема применяется при решении уравнений математической физики методом Фурье. Решение задач Штурма-Лиувилля Вначале рассмотрим уравнение (18) y» + λy = 0. и краевые условия первого рода (19) y(a) = y(b) = 0. Для удобства будем считать, что a = 0 и b = l > 0. К такой задаче можно всегда свести данную задачу, если сделать замену переменной x’ = x — a, при этом вид уравнения не изменится. Вид общего решения уравнения (18) зависит от значений параметра λ. Разберем три случая: 1) λ 0. В первом случае обозначим λ = — k 2 . Тогда характеристическое уравнение r 2 — k 2 = 0 будет иметь действительные различные корни r1 = k, r2 = — k: Поэтому, общее решение дифференциального уравнения запишется в виде y = C1e kx + C2e -kx . Подставим краевые условия в общее решение и получим Следовательно, система имеет только нулевое (тривиальное) решение C1 = C2 = 0. Значит, при λ 2 и получим характеристическое уравнение r 2 + k 2 = 0. Оно имеет комплексные корни r1 = ki и r2 = -ki и общее решение дифференциального уравнения в этом случае запишется в виде y = C1cos kx + C2sin kx. Подставим краевые условия в общее решение: Для того, чтобы эта система имела нетривиальные решения, необходимо и достаточно, чтобы sin kl = 0. Следовательно kl = πn, то есть Обычно постоянный множитель выбирают либо равным единице, либо из условия нормировки: По тому же алгоритму решаются задачи Штурма-Лиувилля следующего вида: и Эти задачи так же, как и предыдущая, при λ 0 не имеют собственных значений. В случае λ > 0 общее решение уравнения записывается в виде y = C1cos kx +C2sin kx, где а) для задачи (23) Для того, чтобы эти системы уравнений имели нетривиальные решения, необходимо и достаточно, чтобы coskl = 0. Следовательно, Собственные функции задачи (23) имеют вид Некоторые отличия возникают при решении задачи Штурма-Лиувилля в случае краевых условий второго рода Рассуждениями, аналогичными тем, которые проводились для краевых условий первого рода, можно показать, что задача (25) при λ 0. В этом случае, общее решение уравнения имеет вид y = C1cos kx + C2sin kx, Эта алгебраическая система имеет нетривиальные решения тогда и только тогда, когда, sinkl = 0 то есть kl = πn или Для задачи Штурма-Лиувилля с краевыми условиями третьего рода (21) уже не удается получить собственные значения в явном виде. В качестве примера рассмотрим одну такую задачу, когда При Получившаяся алгебраическая система будет иметь нетривиальные решения только в том случае, когда coskl — ksinkl = 0 или Уравнение (28) является трансцендентным уравнением относительно k. Оно не решается в явном виде. Однако, построив графики левой и правой частей уравнения (28), видно, что оно имеет бесконечно много решений (см. рис.13). Обозначим корни уравнения (28) через rn, n = 1,2, . . Тогда Численными методами можно найти приближенные значения rn. Из системы (27) при k = rn получим C1n = rnC2n , где C2n -произвольные постоянные. При этих значениях постоянных решения дифференциального уравнения будут иметь вид Они являются собственными функциями краевой задачи (26) с собственными значениями Как было сказано в п. 10.1, в силу основной теоремы существования и единственности решения для уравнения второго порядка Определена задача Коши, когда в точке Х = X0 заданы значения неизвестной функции и ее производной: Если выполнены условия теоремы 10.1, то задача Коши (10.13), (10.14) однозначно определяет частное решение. Однако существует и другой тип задач для дифференциальных уравнений второго порядка — значения неизвестной функции задаются в двух разных точках. Иными словами, при решении уравнения (10.13) на интервале (А, B) рассмотрим Граничные условия наиболее простого вида на концах интервала В этом случае уравнение (10.13) совместно с условиями (10.14) называется Первой краевой задачей для уравнения второго порядка. Поскольку второе условие в (10.15) равносильно второму условию в (10.14), то указанная краевая задача может иметь единственное решение, т. е. определять единственным образом частное решение дифференциального уравнения (10.13), проходящее через точки (X1, Y1), (X2, Y2). Так, для линейного дифференциального уравнения второго порядка первая краевая задача имеет решение, если определитель системы линейных алгебраических уравнений относительно произвольных постоянных C1 и С2 Реализующей краевые условия (10.15), отличен от нуля. Здесь в соответствии с теоремой 10.4 Пример 1. Найти частное решение уравнения Удовлетворяющее краевым условиям Общее решение этого уравнения было найдено в примере 4 и. 10.3: Для отыскания частного решения, соответствующего данным краевым условиям, подставим это решение в эти краевые условия. Получаем систему линейных уравнений относительно произвольных постоянных С1 и С2 Нетрудно видеть, что определитель этой системы не равен нулю, т. е. данная краевая задача имеет решение. Вычитая из второго уравнения первое, умноженное на 2, получаем С2, а затем из первого уравнения — С1: Отсюда решение данной краевой задачи как частное решение дифференциального уравнения, проходящее через точки (0, 1) и (ln 2, 2), имеет вид 4.11.2. Краевые задачи для линейного дифференциального уравнения второго порядка. Общий вид В общем случае линейное дифференциальное уравнение второго порядка имеет вид: Основные типы краевых условий, задаваемых на концах промежутка (изменения независимой переменной x ), на котором решается задача, имеют вид: — условие первого рода — условие второго рода — условие третьего рода На левой и правой границах промежутка могут быть заданы условия одного и того же или разного рода. Если коэффициенты уравнения и правая часть — непрерывные функции, то краевая задача имеет единственное решение. Дифференциальное уравнение вида (28) может быть преобразовано в уравнение в так называемой самосопряженной форме: Для этого умножим обе части уравнения (28) на функцию . С учетом того, что после умножения уравнение (28) можно записать в виде , т.е. в виде (29), где 4.11.3. Построение трехточечной разностной схемы 2-го порядка аппроксимации. Рассмотрим линейное дифференциальное уравнение второго порядка в самосопряженной форме на интервале с краевыми условиями первого рода: Если , , то такая краевая задача описывает стационарное распределение тепла в стержне ( u(x) — температура в точке , — коэффициент теплопроводности). Задача имеет единственное решение, если — кусочно-непрерывные функции. Введем на отрезке равномерную сетку и запишем трехточечную разностную схему для краевой задачи (30)-(31) в прогоночном виде где коэффициенты зависят от значений функций в узлах сетки, а также от шага . Решение системы уравнений (32), (рассматриваемой вместе с граничными условиями) имеющей трехдиагональную матрицу коэффициентов, может быть найдено методом прогонки. Ранее этот метод описан в связи с построением кубического интерполяционного сплайна. Выражения для коэффициентов разностной схемы должны обеспечивать аппроксимацию дифференциального уравнения разностной схемой с определенным порядком ее погрешности. Для получения таких выражений запишем разностную схему (32) в виде где . Схема называется однородной, если ее коэффициенты во всех узлах сетки для любого линейного дифференциального уравнения вычисляются по одним и тем же правилам. Для однородной схемы удобна ее запись с использованием безиндексных обозначений: Найдем погрешность аппроксимации схемы (34): Подставляя эти выражения в (35) и группируя члены относительно функии u и ее производных, запишем погрешность аппроксимации в виде: Условием для того, чтобы схема (34) имела второй порядок аппроксимации, будет выполнение соотношений: Например, эти условия выполняются при 4.11.4. Сходимость разностной схемы. Обозначим погрешность разностной схемы в узлах сетки: . Пользуясь линейностью оператора в уравнении (34) можно установить, что погрешность в узлах сетки удовлетворяет разностной схеме: где — погрешность аппроксимации. Выведем оценку для погрешности в узлах сетки. Из формул (36) следует, что поэтому схема (33) в прогоночном виде (32) запишется следующим образом: Значения — решение схемы (39) можно найти, используя метод прогонки. Запишем соотношение с неизвестными коэффициентами . Подставив в (39) соотношение , получим Таким образом, для получаем рекуррентные формулы: С учетом того, что соотношение (40) принимает вид откуда получаем, что . Теперь можно вычислить все значения , , , по формулам (41), а затем спуститься «вниз» по i от N до 1 и найти все значения по формуле (40). С учетом сделанного выше предположения относительно коэффициентов дифференциального уравнения (30) , из выражения для коэффициента с следует неравенство: , с учетом которого из неравенства (42) получаем Тем самым из (41) следует, что . Поскольку известно, что , то по индукции мы получаем, во-первых, решение схемы (38) в виде рекуррентных формул (40), (41) и во-вторых, справедливость неравенства На этом основании из формулы (40) можно получить неравенство: из которого с учетом, что , получаем неравенство: . Воспользуемся теперь рекуррентной формулой (41) для , умножив обе ее части на положительную величину : Поскольку первый множитель справа — это коэффициент , величина которого меньше единицы, то, следовательно, . На этом основании получаем: с учетом, что . Наконец, поскольку , можно сделать вывод, что Таким образом, для погрешности в узлах сетки     можно записать неравенство Так как , то переходя к нормам, получаем оценку погрешности решения Такая оценка означает, что разностная схема (33) для краевой задачи (30)-(31) при указанных условиях на коэффициенты имеет второй порядок сходимости. Прмечание. Здесь использована равномерная векторная норма 4.11.5. Краевые условия 2-го и 3-го рода. Рассмотрим теперь уравнение (29) с краевыми условиями 2-го или 3-го рода : Будем решать эту задачу с помощью трехточечной разностной схемы (33). Как показано в пункте 4.11.4, схема (33) имеет второй порядок аппроксимации. Если для апроксимации условий (43) использовать простейшие односторонние двухточечные разностные производные, как в методе Эйлера, то краевые условия для разностной схемы запишутся в виде Первое из этих условий позволяет, выражая y0 и сравнивая это выражение с формулой вида (40) для решения yi при i = 0, найти значения . Однако использованные выше разностные производные имеют первый порядок погрешности аппроксимации. Чтобы краевые условия не снижали порядок аппроксции разностной схемы (33), необходимо воспользоваться односторонними разностными аппроксимациями производных, имеющими второй порядок по h. где, как обычно, . Действительно, по формулам Тейлора Аналогично, разностная производная на правой границе имеет вид: При использовании таких формул разностные аппроксимации краевых условий принимают вид: В этом случае для разрешения трехточечной схемы (33) также может быть использован метод прогонки. при i = 1 составляет с краевым условием систему из которой можно исключить , при этом система преобразуется в уравнение с некоторыми вполне определенными коэффициентами . На правом конце отрезка получаем систему из которой можно найти , а затем и все остальные (по рекуррентным формулам (40)). http://matica.org.ua/metodichki-i-knigi-po-matematike/osnovy-matematiki-i-ee-prilozheniia-v-ekonomicheskom-obrazovanii-krass-m-s-chuprynov-b-p/10-4-kraevaia-zadacha-dlia-differentcialnogo-uravneniia-vtorogo-poriadka http://cs.petrsu.ru/studies/complex/part4/part411_a.htm
Те значения параметра λ, при которых задача Штурма-Лиувилля имеет ненулевое решение, называются собственными значениями (собственными числами) задачи, а сами эти решения — собственными функциями. Задачу Штурма-Лиувилля называют также задачей на собственные значения. В силу однородности уравнения и краевых условий собственные функции задачи Штурма-Лиувилля определены с точностью до постоянного множителя. Это означает, что если y(х) -собственная функция при некотором значении λ, то произведение Cy(x), где С — произвольная постоянная, также является собственной функцией при том же значении параметра λ. В связи с этим часто в качестве собственной функции рассматривают нормированную функцию у <х), у которой ||у(х)|| = 1. Такая собственная функция определена, по существу, однозначно (с точностью до знака ±). Далее мы подробно изучим наиболее простой случай задачи Штурма-Лиувилля, когда уравнение имеет видy» + λy = 0. (18) y(a) = y(b) = 0, (19) y'(a) = y'(b) = 0, (20) (21) 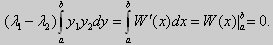
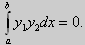
Функции y1(x) 0 и у2(х) 0, поэтому 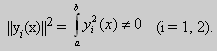
Значит, y1(x) и у2(х) на отрезке [а, b] ортогональны.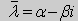
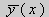
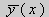
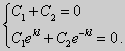
(22) 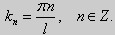
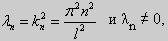
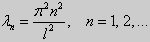
(23) (24) 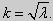
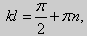
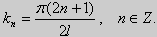
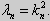
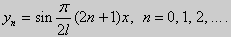
y» + λy = 0, y'(0) = y'(l) = 0. (25) 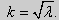
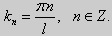
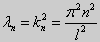
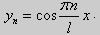
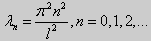
y» + λy = 0, y'(0) = y(0), y'(l) = 0. (26) 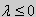
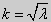
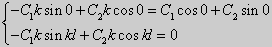
(27) ctgkl = k (28) 
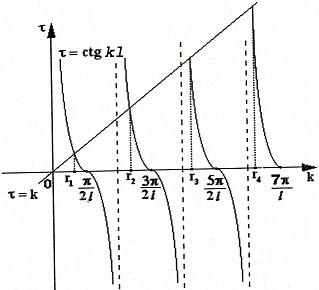
Рис.1310.4. Краевая задача для дифференциального уравнения второго порядка

Решение краевой задачи для линейного дифференциального уравнения
Формулы метода прогонки также приводятся ниже при рассмотрении вопроса о сходимости разностной схемы.
Второе из граничных условий вместе с формулой (40) при i = N позволяет определить значение yN .
Например, для этих целей подходит разностная производная
Уравнение